Errata and Addendum: Magnetic properties of an antiferromagnetic spin-1/2 XYZ model in the presence of different magnetic fields:finite-size effects of inhomogeneity property(2019,Commun.Theor.Phys.71 1253–1260)
Sachin Kumar and S M Yusuf
1 Solid State Physics Division,Bhabha Atomic Research Centre,Mumbai 400 085,India
2 Homi Bhabha National Institute,Anushaktinagar,Mumbai 400094,India
Abstract We report the correct results for the antiferromagnetic s=1/2 XYZ model system considered in(2019,Commun.Theor.Phys.71 1253).We also point out the correct model system used for the reported results therein.
Keywords: spin chain,magnetization,susceptibility
The antiferromagnetic s=1/2 model chain system under the presence of homogeneous as well as inhomogeneous longitudinal,transverse,and staggered transverse magnetic fields takes the following form,
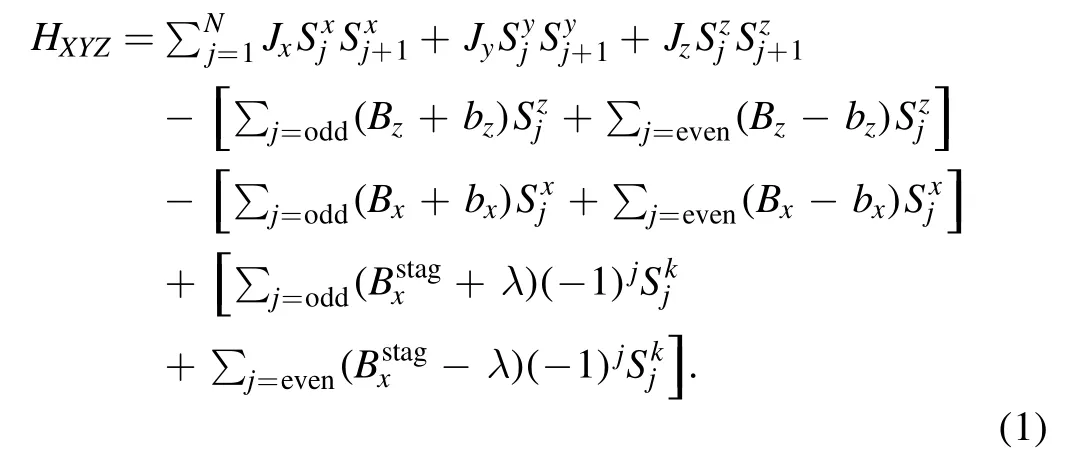
The integers j=(1,2,3,...,N) run over the number of spins,and Jx,Jyand Jzrepresent the nearest neighbor Heisenberg exchange interactions.Sx,Sy,and Szare spin-1/2 operators.Bz,Bxanddenote the uniform longitudinal magnetic field,transverse magnetic field,and staggered transverse magnetic field,respectively.The staggered transverse magnetic fieldBxstagis related to longitudinal field BzasThe degree of inhomogeneity in longitudinal,transverse,and transverse staggered fields is controlled by parameters bz,bxand λ,respectively.We have set the gyromagnetic g-factor and Bohr magneton coefficient μBequal to one in equation (1).We use periodic boundary conditions SN+1=SNfor solving the eigenvalue equation Hψ=Eψ for H in equation (1).

Figure 1.(a) Magnetization M/Ms and Susceptibility X as a function of applied longitudinal magnetic field Bz/Jz for a set of transverse magnetic fields Bx/Jz(colored lines)and low staggered transverse field with θ=π/30 at low temperature(T=0.1Jz)has been plotted.Here bz,bx and λ=0.Jx=8Jz and Jy=10Jz.(a) and (c) correspond to the case k=x in equation (1) for N=6,and similarly (b) and (d)correspond to the case k=z in equation (1) for N=6.
In this note,we will briefly discuss the results of HXYZfor two cases: k=z,x (i.e.Sk=Sz,Sx).The antiferromagnetic s=1/2 chain system considered in equation (1) in (2019,Commun.Theor.Phys.71 1253)[1]corresponds to a case of equation (1) for k=x (i.e.Sk=Sx).Here,we find the magnetization of the antiferromagnetic s=1/2 chain system at low temperature T=0.1Jzin presence of homogeneous magnetic fields keeping inhomogeneous field parameters to zero for N=6.We have taken the conventional Heisenberg exchange interaction constants as Jx=8Jzand Jy=10Jzfor the results in this note.In figure 1(a),we plot the magnetization M/Msof the spin chain system (equation (1)) as a function of Bz/Jzfor the case k=x.We see two weak magnetization plateaus M/Ms=0 and M/Ms=1/3 at different transverse magnetic fields Bx/Jzand a low staggered transverse field with θ=π/30.We see that this result doesn’t match with the magnetization curve reported in figure 2(a)in[1] for the same set of parameters.In figure 1(b),we plot the magnetization M/Msof the spin chain system (equation (1))as a function of Bz/Jzfor k=z (i.e.Sk=Sz).We see the presence of one more plateau M/Ms=2/3 in addition to M/Ms=0 and M/Ms=1/3 plateaus.These plateaus gradually convert to their counterpart quasi-plateaus on increasing the transverse field Bx/Jz.Magnetization M/Mssaturates at a lower Bz/Jzvalue than the magnetization in figure 1(a).This result matches exactly with what is reported in figure 2(a) in[1].Figures 1(c) and (d) show the magnetic susceptibility X for the case k=x and k=z respectively.The rest of the parameters are kept to be the same as used to find the magnetization.Susceptibility shows the peaks in those regions of applied field Bz/Jzat which quasiplateau/plateau arises in the magnetization curve.Peaks in figure 1(c) around Bz/Jz=8 indicates the possible presence of a meager plateau M/Ms=2/3 in the magnetization curve (figure 1(a)) around the same Bz/Jz.Susceptibility displays non-monotone behaviour at zero applied field on increasing transverse field.Susceptibility decreases steeply in strong longitudinal magnetic field region Bz>10Jzfor all values of Bx/Jz.This result again does not match with the corresponding susceptibility result in figure 2(c) in [1],while the susceptibility result for the case k=z plotted in figure 1(d)here matches well with the corresponding susceptibility as reported in figure 2(c) in [1].For a detailed explanation of results,we suggest the paper by the authors in [1].
We also find similar differences in magnetization,and susceptibility results in figure 3 reported in [1] when inhomogeneity in magnetic fields is considered.Same stands for specific heat results in figure 4 reported in [1].
We conclude that the results of the model system considered in [1] are different than what is reported there.We have reported the correct results for the model system considered in equation (1) (i.e.k=x) in [1].We have also pointed out the correct model system (i.e.k=z) used for the results reported in [1].
 Communications in Theoretical Physics2022年8期
Communications in Theoretical Physics2022年8期
- Communications in Theoretical Physics的其它文章
- The second harmonic generation in GaAs/GaAlAs spherical quantum dots under Woods-Saxon plus attractive inversely quadratic potential
- Ground-state and dynamical properties of a spin-S Heisenberg star
- Toy model that explains the regulation of cholesterol on lipid rafts
- The ringing of quantum corrected Schwarzschild black hole with GUP
- Quantum corrections to the thermodynamics and phase transition of a black hole surrounded by a cavity in the extended phase space
- Swampland dS conjecture in mimetic f(R,T)gravity
