Toy model that explains the regulation of cholesterol on lipid rafts

Dongyu Lyu，Tanlin Wei，Lei Zhangand Yong Zhang

School of Physics，Sun Yat-sen University，Guangzhou 510275，China

Abstract Cholesterol，as a common lipid on mammalian cell membranes，plays an important role in the formation of lipid rafts.Recent experiments suggest that the strength of cholesterol’s regulation on lipid rafts can be affected by the length of the unsaturated phospholipid acyl chain on the membrane.In order to understand this observation，a simplified toy model containing three different molecules is proposed in this paper，where the tail length of phospholipids is considered.This model shows the regulation of membrane cholesterol on the phase separation of the lipid mixture and the formation of nano-domains，and also suggests that the configuration entropy of phospholipid tails is an essential factor.

Keywords: cholesterol，tail length of phospholipids，lipid lattice model，phase separation，lipid rafts

1.lntroduction

The cell membrane is a highly lateral heterogeneous medium composed of lipids，proteins and carbohydrates [1].Cholesterol is an essential lipid in mammalian cells，which prefers to interact with saturated phospholipids over unsaturated ones[2–4].It can modulate the acyl chain order of surrounding lipids when present in phospholipid bilayers[5]，and this may lead to the formation of liquid-ordered domains [6]，which were named as lipid rafts by Simons and Ikonen [7].Lipid rafts are relatively ordered dynamic nanoscale domains rich in cholesterol and saturated phospholipids such as sphingolipids on cell membranes [8].Such structures are endowed with membrane protein sorting and signal transduction functions[1，9]，and also play an important role in the process of infection by pathogenic microorganisms [10].

The previous theoretical models to study the formation mechanism of lipid rafts can be roughly divided into two categories.The first one is based on the Ising model.Three components，saturated phospholipids，unsaturated phospholipids，and protein molecules are placed on a lattice in this model[11]，and the formation of lipid rafts can be reproduced by setting different interaction parameters between these molecules.The second one is a nonequilibrium model considering lipid circulation [12–17]，where a lipid reservoir is set up so that lipid can transfer between the membrane and the surrounding medium.The balance of phase separation and permanent lipids exchange leads to the formation of particular domains，whose characteristic size is controlled by the exchange rate of lipids.

It has also been revealed that several factors including temperature [18]，competition between linear tension and curvature [19–22]，and membrane composition [20–24] can all regulate the formation of lipid rafts on cell membranes.In recent years，Nyholm et al suggested that cholesterol，as a primary component of lipid rafts，can promote the formation of liquid-ordered domains on biomembranes [25–27].Their experiments obtained the concentration of saturated phospholipids required for the formation of ordered domains by measuring the fluorescence lifetime，indicating that the intensity of this effect of cholesterol is related to the phospholipid head group [25]，the unsaturation degree of the unsaturated phospholipid acyl chain[26]，as well as the length of the unsaturated phospholipid tail [27].The results show that the shorter the tail chain length，the stronger the regulatory effect of cholesterol on the formation of liquidordered domains.However，in previous theoretical models，lipid molecules were all represented by a mass point occupying on a lattice.Only interaction between molecules can be considered in these models，but not geometric configurations，and as a result，they cannot explain the difference in the influence of cholesterol on lipid rafts caused by various phospholipid tails.

In this paper，we aim to explain the relationship between the regulatory effect of cholesterol on the formation of lipid rafts and the tail length of unsaturated phospholipids，which was observed in experiments，by improving the previous lattice model.Not only the interaction between head groups but also the configurations of tail chains are considered in our model.The free energy of the system is calculated to find the critical molar fraction of saturated phospholipids corresponding to the phase separation，and the influence of the tail length on the phase separation is investigated.It also suggests that the configuration entropy of phospholipid tails plays an essential role in our model.

2.Model

There are three types of molecules in our model，as shown in figure 1.Molecule A consists of a spherical head group and a rigid stick-shaped tail chain that can rotate around the apex connected to the head freely.The structure of molecule B is similar，but with a different head group and a longer tail chain.However，molecule C is only represented by one rigid stick.The head groups of molecules A and B fully occupy a 2D triangular lattice in the model.cAand cB=1 −cArepresent the molar fraction of the two molecules，respectively.Their tails are below the grid plane and can rotate freely in a certain space.The third component，molecule C，is allowed to reside vertically intercalated in the corresponding honeycomb lattice (see figure 2)，φ being its occupancy fraction.The membrane molar fraction of A，B and C components are cA/(1+2φ)，cB/(1+2φ) and 2φ/(1+2φ)，respectively.

In the model we introduce the following four assumptions:

1.Only the interaction between head groups is considered，which means the tail-tail and tail-head interactions are neglected.

2.Molecule C is attracted by A but repelled by molecule B，so molecule C will only appear in the gap near molecule A.

3.The pairs between the nearest neighbor molecules are considered，as shown in figure 3.There will be interdigitation between the tails of the same type of molecules (A–A pair and B–B pair)，however，the tails of molecules A and B will restrict each other’s movement for A–B pair.Moreover，molecule C inserted in the middle will physically block the interleaving for A–A pair and A–B pair.

4.The number of individual molecular pairs does not depend on the distribution of their heads.

First，a binary system with only molecules A and B，which means φ=0，is considered.The entropy of the system includes the mixing entropy of head groups and the configuration entropy of tails，which can be expressed as

Figure 1.Toy models of three different molecules.Molecules A and B are both composed of a head and a rigid stick-shaped tail that can rotate freely in the gray cone，while molecule C is represented by only one rigid stick.

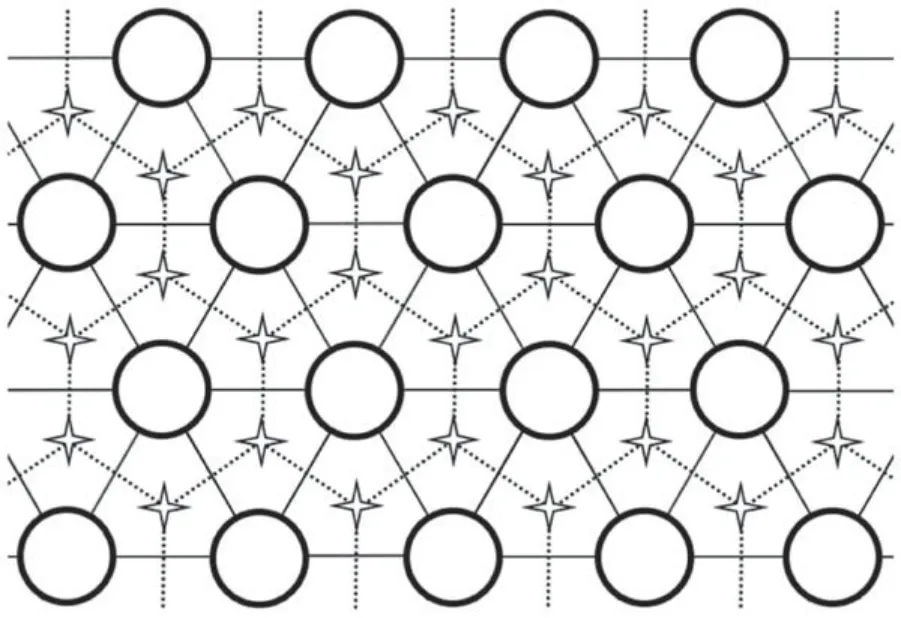
Figure 2.A lattice system filled with model molecules.The heads of molecules A and B fully occupy the triangular lattice of circular nodes.Molecule C is intercalated between the other two components and occupies part of the star nodes forming the honeycomb lattice.

Figure 3.The diagram considering the overlap of the tail motion region between the nearest molecular pair.The heads of molecules A and B are represented by white and dark spheres，respectively.The tails of different molecules limit each other’s range of rotation.

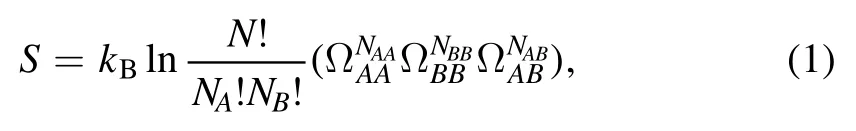
where kBis the Boltzmann constant.NAand NBare the number of molecules A and B in the system，respectively.N=NA+NB，which is also the total number of triangular lattice nodes.ΩAA，ΩBBand ΩABrespectively represent the number of microscopic states corresponding to the tail chain configuration of each A–A pair，B–B pair and A–B pair，and their values are positively correlated with the projection area of the tail motion space in the vertical direction.According to the third assumption，the overlaps between the tail motion regions of molecular pair A–A and B–B are allowed，and as a result，the values of ΩAAand ΩBBare determined by the length of the tail chains of the corresponding molecule.The longer the tail，the larger the corresponding number of microscopic states.As for the A–B pair，the tail motion regions of both molecules are restricted by each other.The value of ΩABis determined by the distance between two lattice nodes，but not the length of the tail.Therefore，the relationship ΩAB＜ΩAA≤ΩBBshould be satisfied.In addition，NAA，NBB，and NABin equation(1)respectively represent the number of A–A pair，B–B pair and A–B pair，which satisfy the constraint

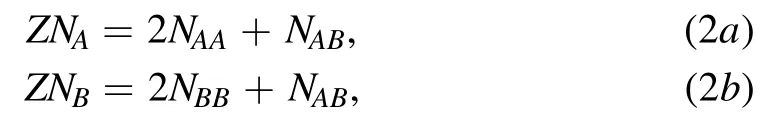
where Z represents the coordination number，which equals 6 in the current model.

According to the Bragg-Williams approximation in the 2D Issing model [28]

which ignores the short-range correlation between molecules，one can rewrite the entropy of the system approximately as

The free energy density of the system in units of kBT reads

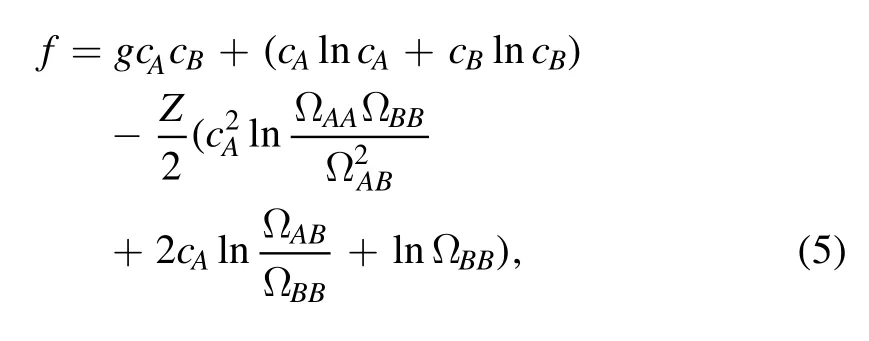
where g=1.9(at T=300 K)is the Flory–Huggins parameter characterizing the interaction between molecules A and B.

Since it is assumed that molecule C will only appear near molecule A，state number ΩAAand ΩABwill become smaller after adding molecule C to the system，and as shown in figure 3，the degree of reduction of ΩABis related to the tail length of molecule B.Therefore，for the ternary system including molecule C，the free energy density can be written as

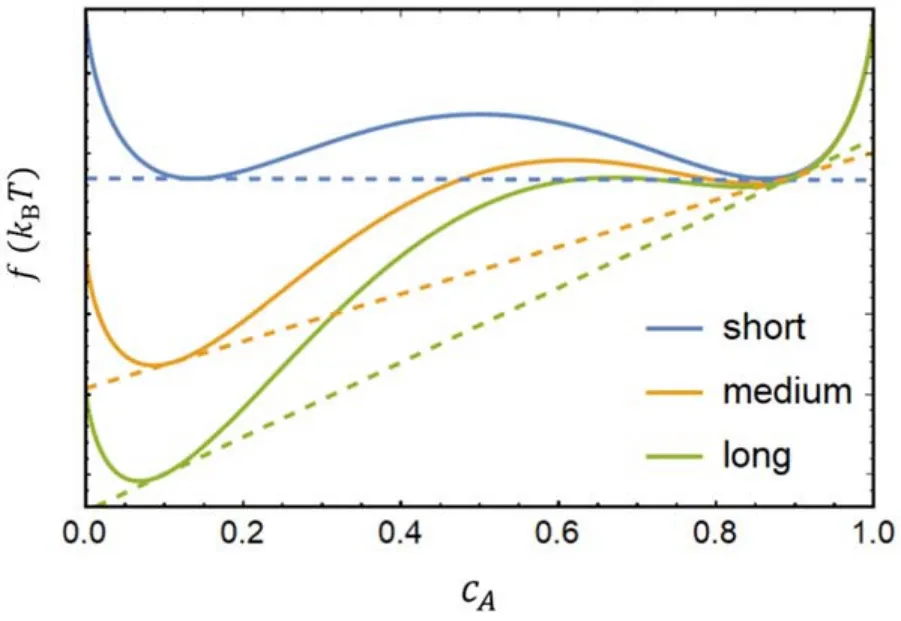
Figure 4.Free energy curves with various tail lengths of molecule B and tangent lines that satisfy the chemical equilibrium.The two tangent points of each curve indicate the critical molar fraction of molecule A in the system for phase separation to occur.Here we only show the curves of systems consisting of molecules A and B(φ=0)as examples.The same calculations can be performed after inserting molecule C into the system，and the phase separation points variation can be obtained.

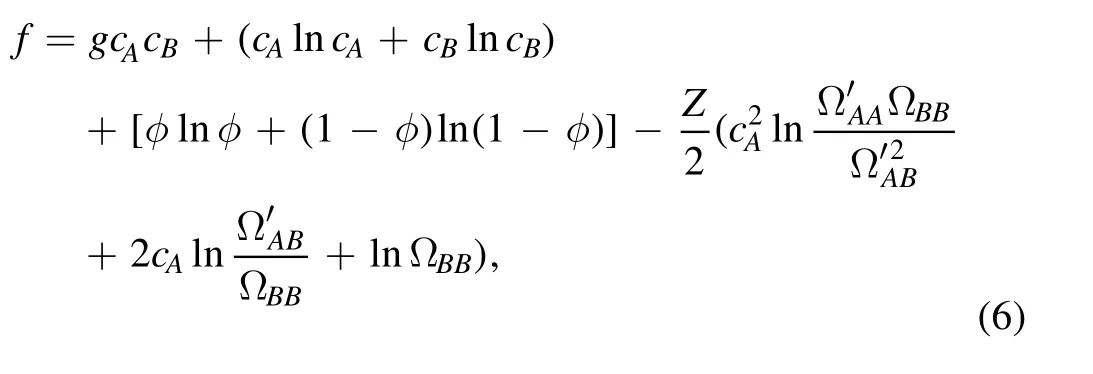
whereandrepresent the new number of microscopic states corresponding to the tail configuration of each A–A pair and A–B pair，respectively，after the insertion of molecule C.

3.Numerical results

One can obtain the critical molar fraction of molecule A corresponding to the phase transition point that satisfies the chemical equilibrium at a given temperature from free energy curves，as shown in figure 4.

The number of microscopic states of the tail configuration ΩAA，ΩBBand ΩABare assigned separately.The value of ΩBBincreases due to the increase in the length of the molecule B's tail.The value of ΩABis only determined by the lattice constant before adding molecule C，however the tail length would affect how much it reduces after molecule C is inserted into the system.The detailed parameters are listed in table 1，as well as the critical molar fraction of molecule A corresponding to the phase transition points before and after the addition of molecule C and the percentage variation.

The calculation results show that the molar fraction of molecular A required for phase separation of the system is reduced after molecular C is incorporated，indicating that molecular C makes the phase separation more likely to occur.Moreover，there is an obvious relationship between the strength of this regulation and the tail length of molecule B.The longer the tail chain of molecule B，the less obvious the regulation effect of molecule C.On the contrary，the shorter the tail of molecule B，the greater the change of the critical molar fraction of molecule A，and the stronger the regulation effect of molecule C on the phase separation of the system.

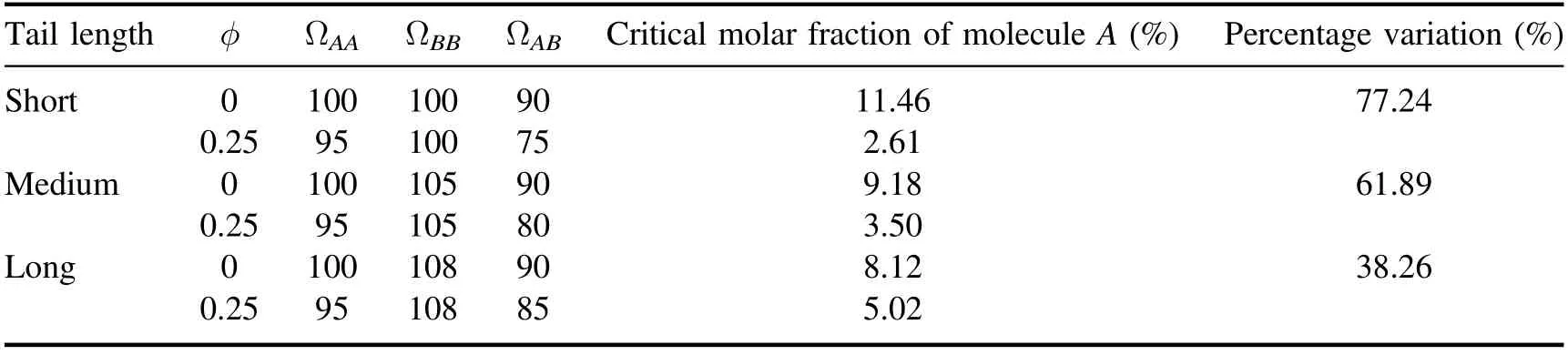
Table 1.The critical molar fraction of molecule A corresponding to the phase transition point.

4.Similarity with lipid rafts

The molecules in our model can respectively correspond to the three main molecules in the lipid raft structure: saturated phospholipids，unsaturated phospholipids，and cholesterol.The rationality of this correspondence is not only reflected in the structural similarity，but also in the introducing assumptions.Cholesterol molecules tend to gather with the tails of saturated phospholipids instead of unsaturated ones [2–4]，which is shown in our second hypothesis.And as for the third one，we will further explain it through the following cavity calculations.

4.1.Cavity formation

In our model，only the interdigitation between the tails of the same molecule is considered，and the entanglement between molecules A and B is ignored.In other words，when one single molecule B is surrounded by a group of molecule A，a cavity will be formed.The tail of B can move freely in this cavity，but it cannot be extended out of the limited area.

We consider an elastic flat membrane system composed entirely of molecule A，with only one molecule B incorporated in its center and causing elastic deformation.The free energy of the system reads [29，30]

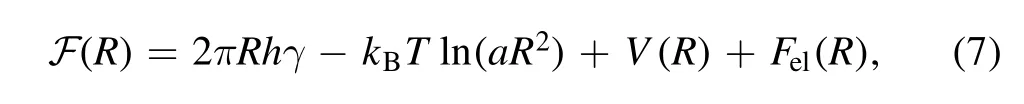
Figure 5.The partial derivative of the free energy of an elastic system with respect to the radius of the cavity.

The radius of the cavity can be obtained by optimizing the free energy with respect to R，= 0.The other parameters in the model are set as follows according to related experiments: h=2.5 nm，γ=0.28–1.4 μN.m−1[33，34]，T=300 K，G=2–6 μN.m−1[35，36].Two parameters in the LennardJones potential energy，σ12and σ6，are obtained from the interaction parameters between C1 (saturated) and C4(unsaturated)carbon beads in the Martini force field[37–39].The influence of the value of the phenomenological parameter Jm(between 1 and 107) on the optimal radius is negligible，and numerically calculated radius R is always 0.53 nm (see figure 5)，which is smaller than the typical distance between phospholipids on biomembranes.In other words，the tail of molecule B is confined to a cavity with a radius of 0.53 nm，which illustrates the rationality of the assumption that different phospholipid tails restrict each other’s movement.

4.2.Comparison with experimental results

The experimental data reported by Nyholm et al in 2019 shows that the regulation of cholesterol on lipid raft formation is significantly affected by the tail length of the unsaturated phospholipid on the membrane [27].The concentration of saturated phospholipids required to form liquid-ordered domains drops significantly after adding cholesterol to the membrane.Moreover，the strength of the regulation is affected by the length of the unsaturated phospholipid tail chains.The longer the tail，the smaller the percentage variation，and the weaker the regulation of cholesterol.

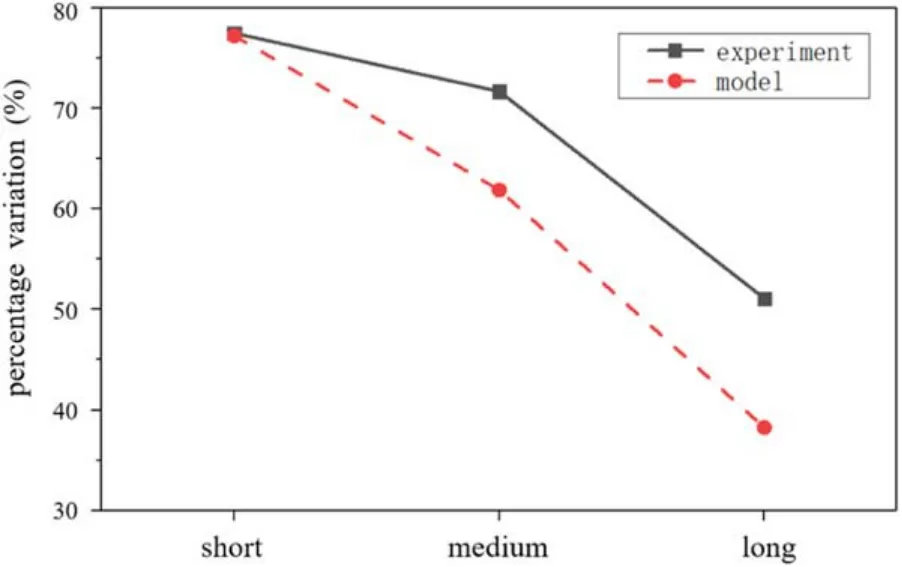
Figure 6.Comparison between experimental and model results indicates the relationship between the effect of cholesterol on lipid raft regulation and the length of unsaturated phospholipid tails.The experimental data are obtained from reference [27].

The calculated influence of molecular C on the phase separation regulation of the system from table 1 is plotted in figure 6，and the result qualitatively agrees with the experimental curve.It is a verification of the validity of our model，and it also shows that the model proposed in this paper has certain application values in explaining the regulation of cholesterol on the formation of lipid rafts.

In our model，the length of the unsaturated phospholipid tail chain is reflected by the configuration entropy of the tail.Therefore，it suggests that entropy plays an important role in the result that the regulation of cholesterol on lipid rafts varies with the length of the unsaturated phospholipid tails.After adding cholesterol to the system，the motion space of phospholipid tails is inhibited，which reduces the entropy of the system and increases the free energy.The phase separation is conducive to the energy reduction of the system，so the addition of cholesterol makes the system easier to form liquid-ordered microdomains.And the longer the tails of unsaturated phospholipids，the smaller the change of the configuration entropy after the addition of cholesterol，and as a result，the weaker the regulation effect on the formation of lipid rafts.

5.Conclusion

A toy model system is proposed in this paper，which is applied to the explanation of the regulation effect of cholesterol on lipid rafts in experiments.There are three molecules in the system.Molecules A and B are both composed of a spherical head and a rigid stick-shaped tail，which completely fill the 2D triangular lattice.Molecule C only has one single rigid tail，which is inserted in the corresponding honeycomb lattice.

By calculating the free energy of the system，the critical molar fraction of molecule A required for the phase separation of the system can be obtained.The results show that the addition of molecule C can make phase separation of the system more likely to occur.Moreover，the strength of this regulation effect of molecule C is significantly dependent on the tail length of molecule B.The shorter the tail，the stronger the influence of molecule C on the phase separation.The similarity between the proposed model and the lipid raft system is also discussed in the paper，and the calculation of the cavity in an elastic medium shows that the assumptions in our model are reasonable.The results of our model are compared with the experimental results，which shows the validity.

Our toy model theoretically explains the conclusion observed in the previous experiment and suggests that the entropy contributed by the motion region of the phospholipid tails is an important factor.Moreover，our model is highly simplified.In addition to phospholipid and cholesterol molecules，there may be other molecules or objects that also fit the characteristics described in the model，which gives it a wider application potential.

Acknowledgments

The authors acknowledge fiancial support from the National Natural Science Foundation of China (NSFC No.61 475 196).