The second harmonic generation in GaAs/GaAlAs spherical quantum dots under Woods-Saxon plus attractive inversely quadratic potential

Xuechao Li，Yiming Duan and Yongrui Ma

School of Mechanics and Optoelectronics Physics，Anhui University of Science and Technology，Huainan 232001，China

Abstract We examine the profile of second harmonic generation (SHG) for GaAs/GaAlAs spherical quantum dots (QDs) of Woods-Saxon (WS) plus attractive inversely quadratic (AIQ) potential under the joint influence of additional factors (pressure and temperature) and structural parameters (strengths and radius).The energies and wave functions in GaAs/GaAlAs spherical QDs under WS-AIQ limiting potential are calculated using the parametric Nikiforov-Uvarov(NU)method.Depending on the calculated energies and corresponding wave functions，the SHG coefficient is examined by the iterative procedure in the density matrix method for this system.Finally，the calculated results display that a strong SHG coefficient response，and red shift or blue shift energy can be acquired by adjusting parameters.

Keywords:second harmonic generation，quantum dots，structural parameters，Nikiforov-Uvarov method

1.lntroduction

Laser is the most significant innovation of the 20th century after nuclear energy，the computer，and semiconductors.The emergence and development of laser has not only led to a lot of new science，its research has had an important impact on the daily life of today’s society [1–4].Nonlinear optics is one of the disciplines accompanying the emergence of laser and is a branch of modern optics[5–8].Its main research direction is the nonlinear phenomenon and its application under the interaction between laser and matter.Unlike traditional linear optics，which use a relatively weak common light source，nonlinear optics uses lasers with high intensity as a light source，which breaks many traditional laws in the propagation process of linear optics，resulting in changes in light frequency，mutual transfer of light energy，and changes in the spatial distribution of outgoing light[9，10].A series of special nonlinear optical effects of materials under the action of laser are of great significance to the research of laser technology，the development of spectroscopy，and the analysis of material structure [11–13].With the continuous research on nonlinear optics，many advantages and important applications of nonlinear optics have been found，which makes it more and more widely used in all optical switches，optical limiters，optical frequency conversion，optical pulse compression，hyperfine material structure analysis and so on [14–16].

In recent decades，low-dimensional semiconductor nanomaterials such as superlattices，quantum wells，quantum wires and quantum dots have been very active research fields.The researchers have made outstanding achievements in both theoretical and experimental research [17，18].Semiconductor QDs are three-dimensional limited semiconductor nanostructures.Quantum confinement effects at the nanoscale can cause the energy levels of semiconductor QDs to be similar to the discrete energy levels of atoms，so semiconductor QDs are also known as‘artificial atoms’.By controlling the shape and size of QDs，we can effectively adjust their energy level structure，which greatly expands the application field of semiconductor devices and makes them have a very broad application prospect in optical quantum information communication [19，20].Therefore，many researchers have done a lot of research on the nonlinear optical properties of QDs.In 2014，H Bahramiyan et al[21]reported the optical properties in the GaAs pyramid QDs: SHG and thirdharmonic generation.In 2016，J Ganguly et al[22]examined the optical SHG of impurity-doped QDs with Gaussian white noise.In 2017，M El Haouari et al [23] reported the nonlinear optical properties of AlAs/GaAs spherical core/shell QDs.In 2020，C Wang et al [24] investigated the nonlinear optical properties for InP/ZnS coreCshell QDs.In 2021，M Choubani et al [25] analyzed the enhancement of the SHG of coupled lens-shaped QDs under the electric field effect.It should be noted that the sphere of WS potential energy and its deformation form was originally used in nuclear calculation.K J Oyewumi et al combined the inverse quadratic potential with the isotropic harmonic oscillator in n-dimensional space.However，up to date，nonlinear optical properties of GaAs/GaAlAs spherical QDs are not fully understood yet under WS-AIQ confinement potential.Strong nonlinear optical response is very necessary for the manufacture of QDsbased optical devices，so we need to consider additional factors in the system to ensure the strongest nonlinear optical response.

In the present paper，we inspect the effect of additional factors on the SHG of spherical QDs under WS-AIQ limiting potential.The structure of this document is as follows: in section 2，we give the system model and explain the relevant theoretical knowledge.Then，the corresponding energy eigenvalues and their corresponding envelope functions are numerically calculated using the parametric NU method.After that，we give the analytical expression of the SHG coefficient by the method of compact density matrix.In section 3，we present the obtained results and corresponding analysis.Finally，the last section is committed to conclusions.

2.Model and analysis

Under the effective mass approximation，the radial Schrödinger equation for a confined electron is written as follows

where V(r) is the limiting potential of our system，m*(P，T)denotes the electronic effective mass under the influence of P，T [26，27].Then，the confining potential V(r) is regarded as the WS-AIQ potential [28–31]

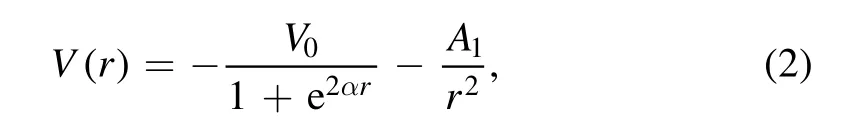
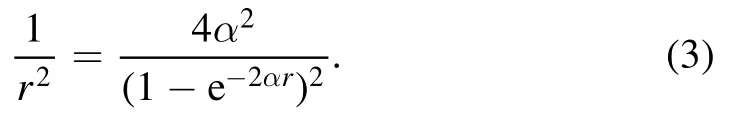
Substituting equations (2)–(3) into (1) and using the coordinate transformation s=e−2αr

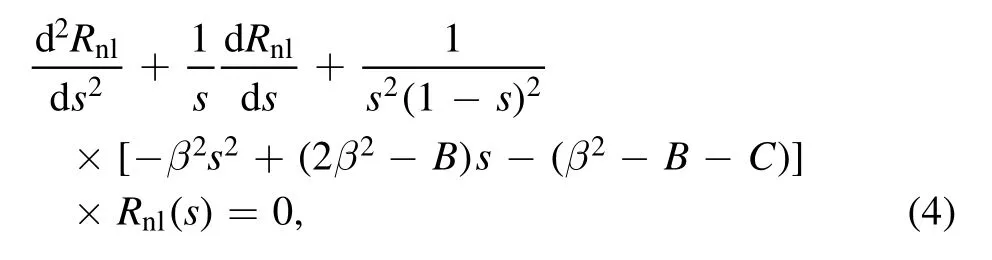
where

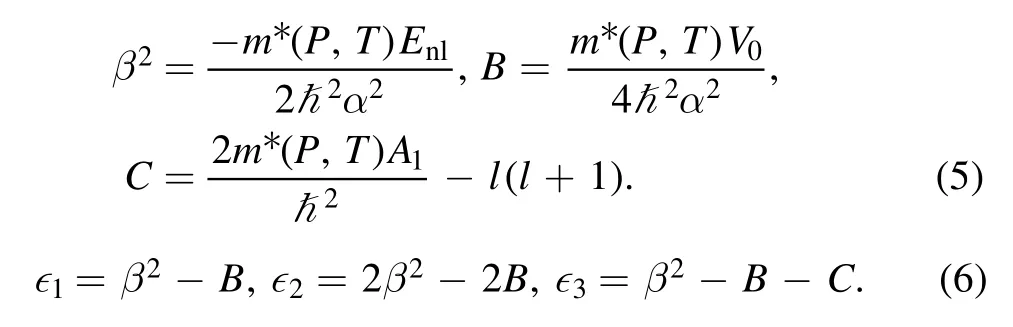
The parametric NU method can be demonstrated by a generalized hypergeometric equation [33–35]

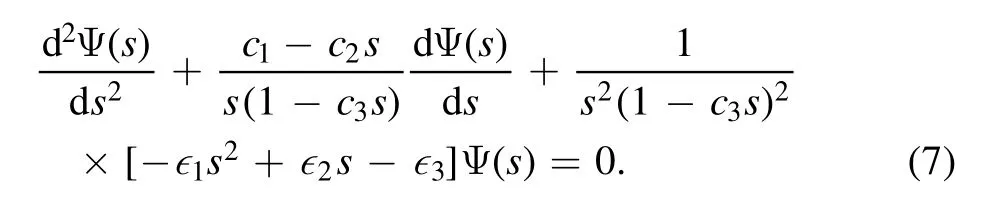
The parameters in the above formula satisfy the following formula

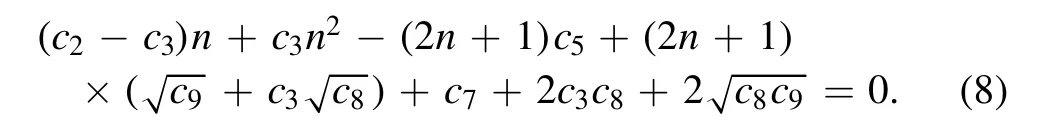
Comparing equations(4)–(6)with (7)，we can obtain the values of the following parameters

To obtain the energy equation of the system，we substitute the parameters’ values in equations (9) into (8)

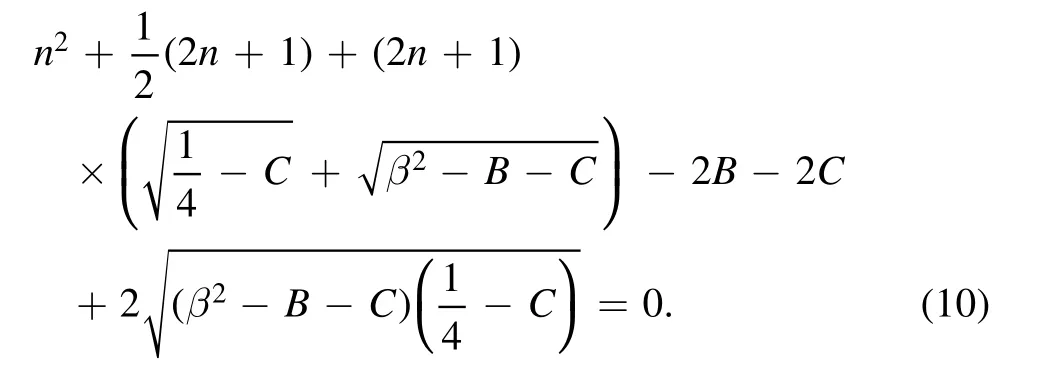
Table 1.Numerical results of dipole matrix elements and transition energies.

By solving equation (10)，we obtain the energy eigenvalue of the system

Similarly

where

The analytical expression of the SHG coefficient of spherical QDs can be calculated by the density matrix method and iterative procedure.The coefficient of the SHG expression is derived [36，37]

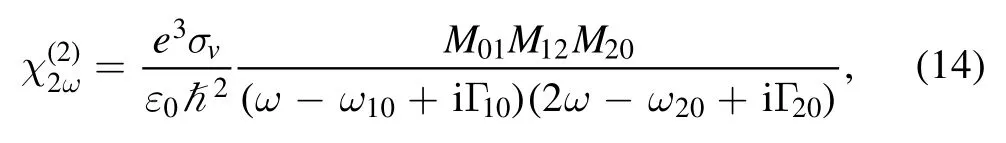
where σvrepresents the density of electrons in the QDs，Mij=|〈Ψj|s|Ψi〉| represents the dipole matrix elements，represents the transition frequency.

3.Results and discussions

In this part，numerical calculations are carried out for GaAs/GaAlAs spherical QDs on the SHG coefficient under the WSAIQ limiting potential.The calculations are executed using the following parameters: [36–38]: σv=5×1024m−3，Γ10=Γ20=1/T1，T1=0.2 ps，ε0=8.85×10−12Fm−1.

In our study，we have calculated GaAs/GaAlAs spherical QDs of dipole matrix elements and transition energies in table 1.These results can reflect the amplitude and resonance frequency of the SHG coefficient.In figure 1，we present the computed SHG coefficient for this system as a function of ÿω，the strength V0is changed from 80 to 120 meV for other fixed parameters (P=10 kbar，T=300 K，R0=6 nm，V1=50 meV).In figure 1，we observe that the difference between E20/2 and E10resulted in the two peaks phenomenon of the SHG coefficient.Besides，E20/2 corresponds to the first low energy peak and high amplitude，E10corresponds to the second peak with the higher energy and lower amplitude in figure 1.The numerical results in table 1 correspond to this phenomenon.We find that the increase of V0leads to an obvious blue shift in the position of the SHG coefficient and a decrease in the peak amplitude.This result is because an enlargement of V0leads to an increment of energy levels difference and a decrement of dipole matrix elements M01M12M20.The energy difference between transition states and matrix elements are two significant factors in the study of the SHG coefficient.The transition energy determines the position of the SHG coefficient in the energy spectrum，and the matrix element determines the size of the peak.

In figure 2，the SHG coefficient is displayed for several different R0as P=10 kbar，T=300 K，V0=100 meV，V1=50 meV.By increasing the R0，the resonance peak of the SHG coefficient suffers the red shift.This phenomenon is explained by the quantum confinement effect.The increase of R0will weaken the quantum confinement of QDs，and then the energy level spacing of confined electrons in QDs will decrease.Therefore，the SHG coefficient shift towards higher energies.Moreover，the magnitude of the SHG coefficient increases significantly with the enhancement of R0，which is due to the increment in the M01M12M20.The physical reason is that by increasing R0，the overlap of different electronic states increases，which makes M01M12M20larger.

Figure 1.SHG coefficient as a function of photon energies for P=10 kbar，T=300 K，R0=6 nm，V1=50 meV with different values of V0.

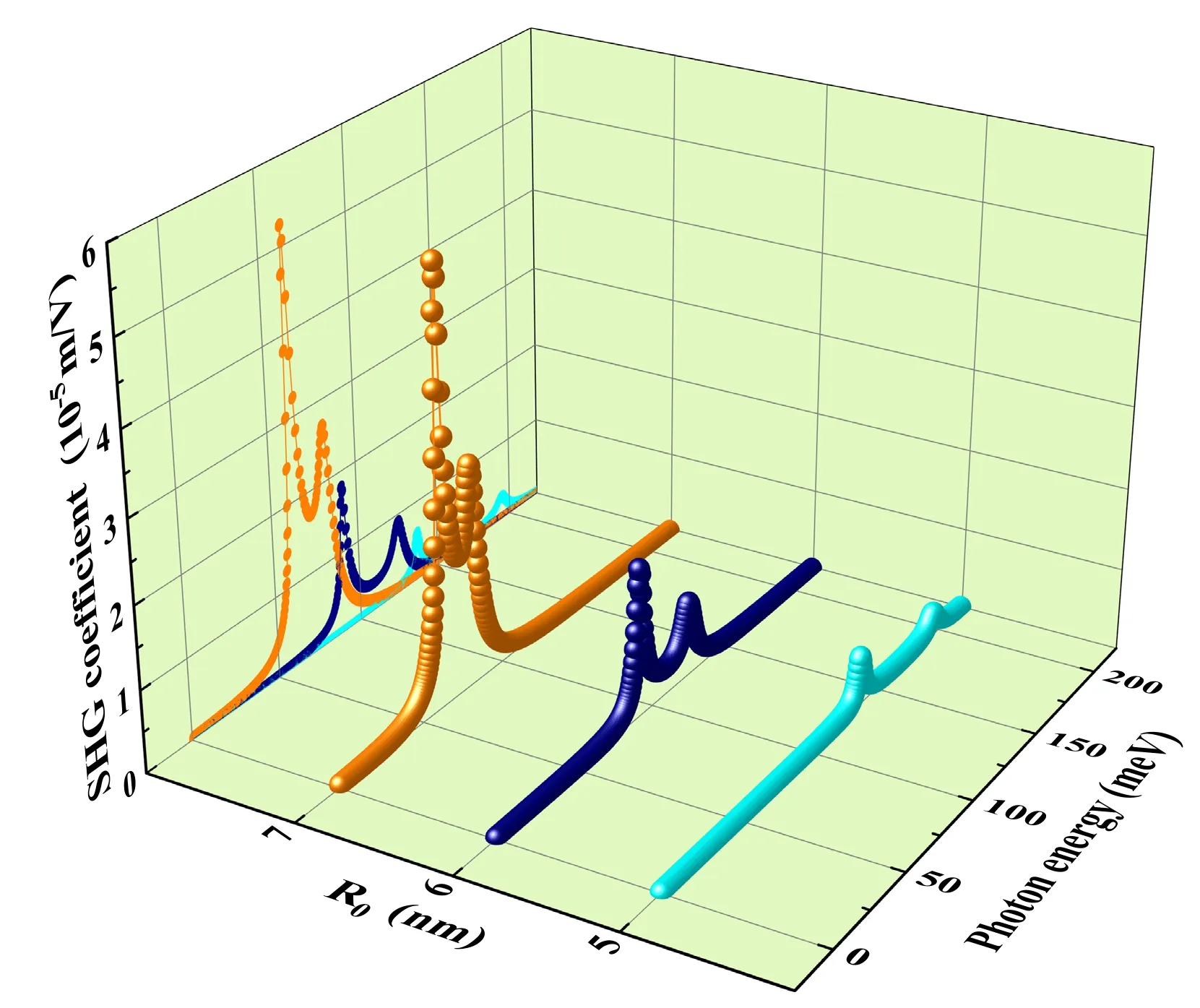
Figure 2.SHG coefficient as a function of photon energies for P=10 kbar，T=300 K，V0=100 meV，V1=50 meV with different values of R0.

Figure 3.SHG coefficient as a function of photon energies for R0=6 nm，T=300 K，V0=100 meV，V1=50 meV with different values of P.

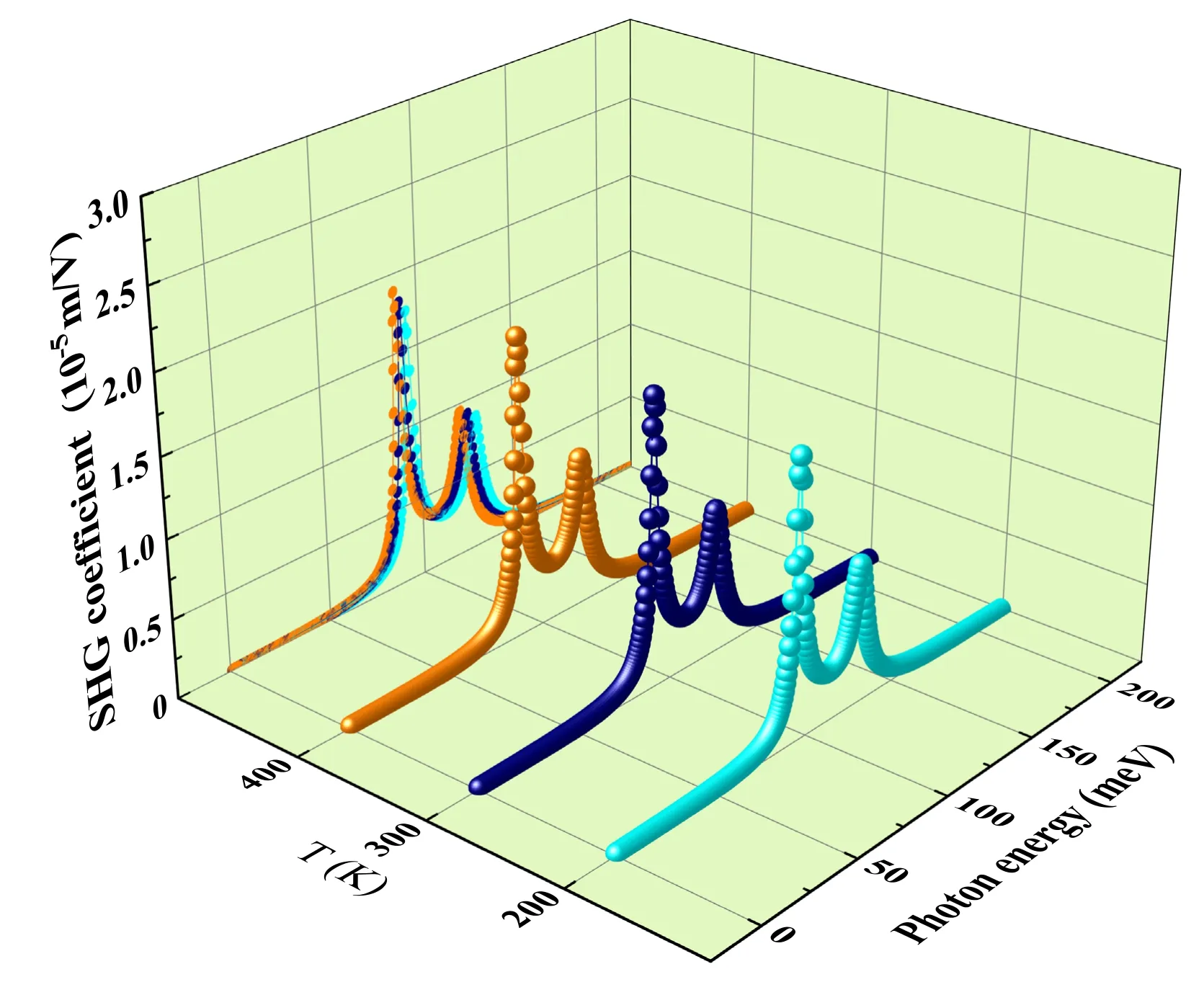
Figure 4.SHG coefficient as a function of photon energies for P=10 kbar，R0=6 nm，V0=100 meV，V1=50 meV with different values of T.

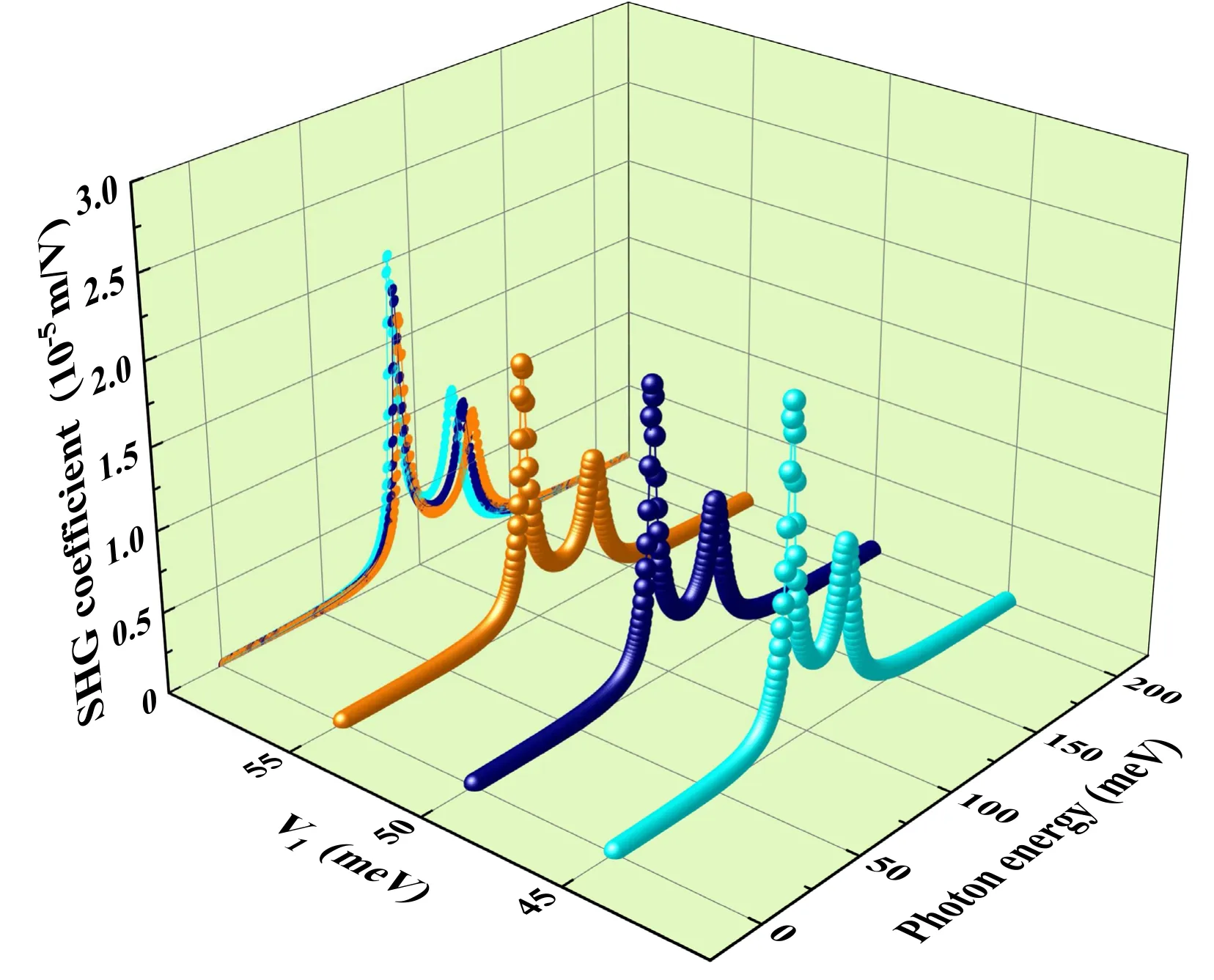
Figure 5.SHG coefficient as a function of photon energies for P=10 kbar，R0=6 nm，V0=100 meV，T=300 K with different values of V1.

Figure 3 represents the variation of the SHG coefficient for different situations of P with R0=6 nm，T=300 K，V0=100 meV，V1=50 meV.The increased pressure effect will cause the SHG coefficient to move in the direction of greater photon energy.This is because the energy level difference determines the position of the SHG coefficient in the energy spectrum.The physical reason is that P has a similar effect on increasing constraints.Furthermore，the stronger P is，the smaller the peak value of the SHG coefficient.The numerical results in table 1 correspond to this phenomenon.

In figure 4，we display the SHG coefficient depending onwith different situations of temperature as P=10 kbar，R0=6 nm，V0=100 meV，V1=50 meV.The increased T will cause a weak red shift in the SHG coefficient.This appearance can be explained by the slight decrease of E20/2 and E10due to the increase of T.From the point of physical reasons，the increase of T reduces the constraints and thus reduces the energy required for subband energy level conversion.In addition，when T changes from 200 K to 400 K，the maximum value of the SHG coefficient increases slightly.

Figure 5 displays the SHG coefficient for different values of V1with P=10 kbar，R0=6 nm，V0=100 meV，T=300 K.We should mention that as V1increases，the SHG coefficient moves to the higher energy region，called the ‘blue shift’.Furthermore，the decrease of the M01M12M20with the increase of V1.This phenomenon brings about a decrease in the maximum value of the SHG coefficient.The physical reason is that the overlap of state wave functions is reduced.In any transition studied，the smaller the overlap of wave functions of states，the smaller the M01M12M20is.

4.Conclusion

In our work，the energy levels and the envelope wave functions for a confined electron in WS-AIQ potential spherical QDs are calculated by the parametric NU method.The analytical expression of the SHG coefficient is obtained using the density matrix approach.We find that the SHG coefficient changes significantly with the variation in pressure，temperature，strengths and QD radius.Because the peak amplitude and position rely on the change of transition energies and dipole matrix elements.Besides，the results indicate that the nonlinear optical properties can be adjusted according to the needs by changing these parameters.We hope that the research results will open up new opportunities for the development of nonlinear optical properties of low-dimensional nanometer material.

Acknowledgments

We would like to thank the National Natural Science Foundation of China (Grant Nos.51 702 003，61 775 087，11 674 312，52 174 161 and 12 174 161)，the Provincial Foundation for Excellent Top Talents of Colleges and Universities of Anhui Province of China (Grant No.gxgwfx2019016)，the Anhui Provincial Natural Science Foundation，China(Grant Nos.1 808 085ME130 and 1 508 085QF140)，University Outstanding Young Talents Support Program Fund (Grant No.gxyqZD2018039).

ORClD iDs