Ground-state and dynamical properties of a spin-S Heisenberg star
Jiaxiu Li and Ning Wu
1 Center for Quantum Technology Research,School of Physics,Beijing Institute of Technology,Beijing 100081,China
2 Key Laboratory of Advanced Optoelectronic Quantum Architecture and Measurements(MOE),School of Physics,Beijing Institute of Technology,Beijing 100081,China
Abstract We generalize the Heisenberg star consisting of a spin-1/2 central spin and a homogeneously coupled spin bath modeled by the XXX ring[Richter J and Voigt A 1994 J.Phys.A:Math.Gen.27 1139-1149]to the case of arbitrary central-spin size S <N/2,where N is the number of bath spins.We describe how to block-diagonalize the model based on the Bethe ansatz solution of the XXX ring,with the dimension of each block Hamiltonian ≤2S+1.We obtain all the eigenenergies and explicit expressions of the sub-ground states in each l-subspace with l being the total angular momentum of the bath.Both the eigenenergies and the sub-ground states have distinct structures depending whether S ≤l or l <S.The absolute ground-state energy and the corresponding l as functions of the intrabath coupling are numerically calculated for N=16 and S=1,2,…,7 and their behaviors are quantitatively explained in the weak and strong intrabath coupling limits.We then study the dynamics of the antiferromagnetic order within an XXX bath prepared in the Néel state.Effects of the initial state of the central spin,the value of S,and the system-bath coupling strength on the staggered magnetization dynamics are investigated.By including a Zeeman term for the central spin and the anisotropy in the intrabath coupling,we also study the polarization dynamics of the central spin for a bath prepared in the spin coherent state.Under the resonant condition and at the isotropic point of the bath,the polarization dynamics for S >1/2 exhibit collapse-revival behaviors with fine structures.However,the collapserevival phenomena are found to be fragile with respect to the anisotropy of the intrabath coupling.
Keywords: central spin model,Heisenberg XXX chain,ground state,antiferromagnetic order relaxation,polarization dynamics
1.Introduction
Quantum spin systems are important physical systems that can exhibit many-body effects and strong correlations.They are ubiquitous in quantum magnetism,statistical physics,and more recently,quantum information and quantum simulations.It is generally challenging to theoretically study many-body spin systems due to the exponential growth of the dimension of the relevant Hilbert space with the system size.In this context,exactly soluble spin models play an important role in understanding the groundstate and dynamical properties of general large-scale spin systems.
Two important classes of soluble spin models are spin chains[1]and central spin models[2,3],which can be solved by using free-fermion techniques or the Bethe ansatz.Currently,typical quantum spin chains such as the quantum Ising model and the XXZ chain have been realized on different experimental platforms [4,5] and continue to attract the attention of theorists[6,7].Central spin models are highly relevant to solid-state setups that are promising candidates for performing quantum information processing,including electrons trapped in quantum dots [8] and nitrogen vacancy centers in diamond [9],etc.
In an early theoretical work,Richter and Voigt proposed a spin model that combines the above two types of soluble models,i.e.a spin-1/2 central spin model and an antiferromagnetic XXX periodic chain [10],with the intention of investigating the effect of central-spin induced frustration on the ground-state properties of the latter.Such a composite spin system,named a Heisenberg star,is originally considered as an antiferromagnetic chain with a perturbation and has several conserved quantities that ensure the solvability of the model.Alternatively,the Heisenberg star can also be viewed as a central spin system in the presence of nearest-neighbor intrabath interactions.Recently,the solvability and real-time dynamics of higher-spin central spin models with/without intrabath interaction are studied and a richer variety of physical properties are observed compared to the spin-1/2 counterpart [11,12].
In this work,we extend the spin-1/2 Heisenberg star to the case of a higher central spin of size S ≤N/2,where N is the number of sites in the XXX ring.Following [13],in which the coherence dynamics of a spin-1/2 Heisenberg star in the presence of an external magnetic was studied,we first describe how to block-diagonalize a spin-S Heisenberg star based on the Bethe ansatz solutions of the XXX ring.The dimensions of the resultant block Hamiltonians are at most 2S+1.With the help of the conserved quantities of the system,we then obtain all the eigenenergies of the model in terms of the quantum numbers l and j,where l and j are the total angular momenta of the XXX bath and the whole system,respectively.Similar to the case of S=1/2,the sub-ground state energy in the l-subspace depends only on l.However,we find that these sub-ground state energies have different structures depending whether S ≤l or l <S.Based on these results,we numerically calculate the absolute ground state energy and the corresponding bath angular momentum as functions of the intrabath coupling for an XXX bath of N=16 sites.The dependence of these quantities on varying S is analytically analyzed in the weak intrabath coupling.We derive closedform expressions of the 2j+1 degenerate sub-ground states in the l-subspace,which can be written as a sum of tensor products of the central-spin state and the degenerate sub-ground states of the XXX bath,with the coefficients being determined analytically.
We are also interested in the real-time dynamics of the Heisenberg star.As observed in[13],for a star prepared in a pure state,the dynamics of any observable belonging to the central spin do not depend on the intrabath coupling,and hence are equivalent to the result for a noninteracting bath.Rather than focusing on the central spin dynamics,we study the staggered magnetization dynamics within the XXX bath when it is prepared in the Néel state.This is motivated by a theoretical investigation of the relaxation of antiferromagnetic order in a spin-1/2 XXZ chain following a quantum quench [14].We reveal the influence of central-spin size,the central-spin initial state,and the system-bath coupling strength on the staggered magnetization dynamics.Some of the observed dynamical behaviors are consistent with those obtained in an inhomogeneous Heisenberg star [12].For example,increasing the size of the central spin and adopting a superposed central-spin initial state can both accelerate the initial decay of the antiferromagnetic order,while these effects become less prominent in the strong intrabath coupling regime.It is intriguing that although the central spin dynamics are independent of the intrabath coupling,the magnetic order within the bath exhibits rich and robust dynamical behaviors even for homogeneous system-bath coupling.
We finally study the central-spin polarization dynamics for a slighted modified spin-S Heisenberg star in the presence of an external magnetic field and with anisotropic intrabath coupling.Following [15–17],we choose the spin coherent state as the bath initial state.We demonstrate that at the isotropic point of the bath the central spin dynamics from the spin coherent state are the same as that for a noninteracting bath.For an XXX bath with S=1/2,we recover the prior results presented in[16].For S >1/2,we find that the polarization dynamics exhibit collapse-revival behaviors with fine structures under the resonant condition.However,the collapse-revival phenomena are destroyed once the anisotropic intrabath coupling is introduced.
The rest of the paper is organized as follows.In section 2,we introduce the spin-S Heisenberg star and its conserved quantities.In section 3,we study the eigenenergies of the model in detail and obtain expressions of the sub-ground state energies in each l-subspace.In section 4,we describe the block diagonalization procedure using the Bethe ansatz solution of the XXX bath and derive explicit expressions for the degenerate sub-ground states in each l-subspace.In section 5,we study in detail the dynamics of the Heisenberg star for baths prepared in the Néel state and the spin coherent state.Conclusions are drawn in section 6.
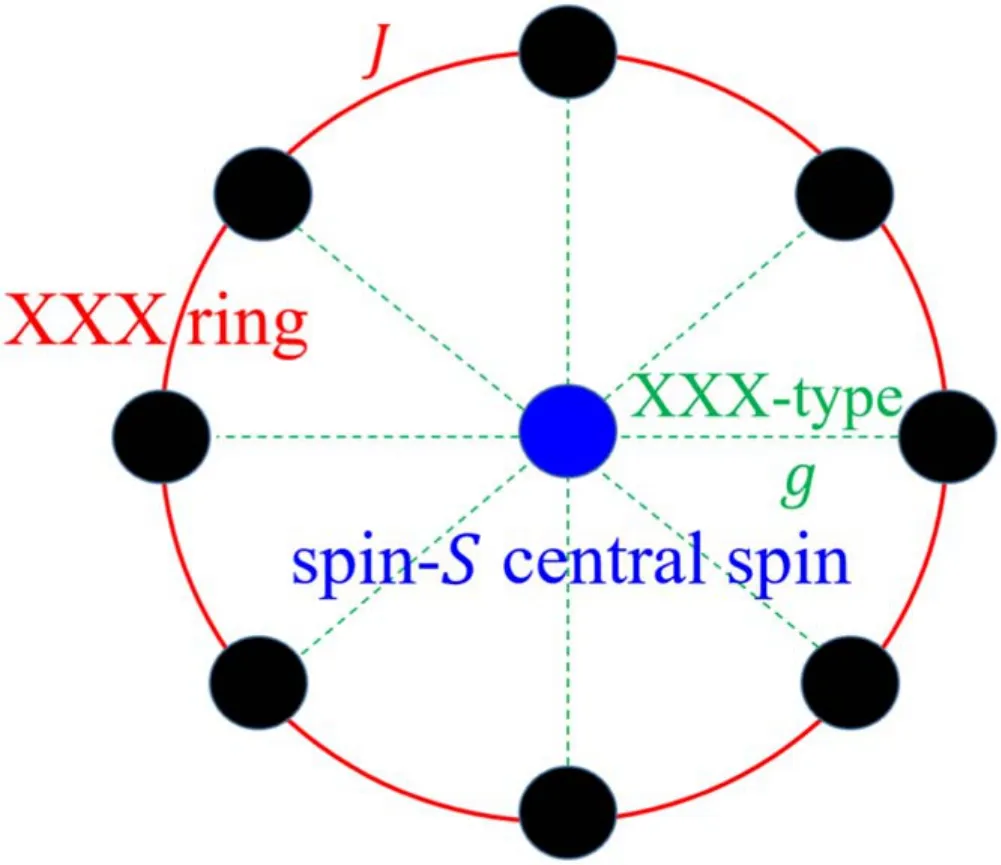
Figure 1.A spin-S Heisenberg star consists of a central spin of size S and a homogeneously coupled XXX ring.The system-bath(intrabath) coupling is of XXX-type with strength g (J).
2.Model and conserved quantities
The Heisenberg star was first introduced in [10] and is described by the Hamiltonian (see figure 1)

Here,HBdescribes a spin-1/2 periodic Heisenberg XXX spin chain with antiferromagnetic nearest-neighbor coupling strength J >0.The interaction between the central spinwith size S and the XXX spin bath is of isotropic Heisenberg type and the coupling strength is measured by g >0.The static properties of H for S=1/2 were studied in detail in[10],but here we allow for arbitrary values of S with S <N/2.
We define the total spin of the whole system as

where

is the total spin of the XXX bath.We can rewrite HSBin terms ofandas

It is easy to check the following commutation relations
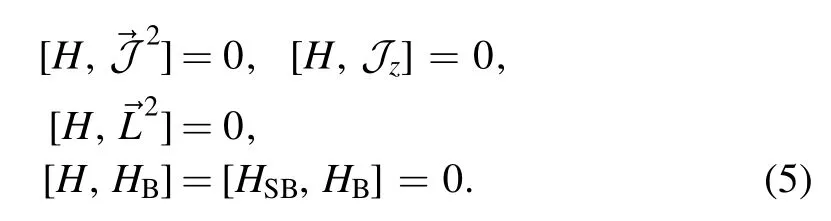

3.Eigenenergies
All the eigenenergies of the spin-S Heisenberg star can be determined from equation (6) once the spectrum of the bath Hamiltonian Hbis solved.We first review the eigenenergy structure of an isolated XXX ring,based on which we construct all the eigenenergies of the Heisenberg star.
3.1.Energy levels of an isolated XXX ring
For completeness,let us first review some known results about the pure XXX ring described by Hb.It is well known that the eigenenergies and eigenstates of the XXZ chain can be solved by using the coordinate Bethe ansatz within individual sectors possessing fixed magnetization [1].For the isotropic XXX chain,the total angular momentumL→is further conserved,yielding simpler state structures and increasing degrees of the degeneracy of the energy levels.

leading to a consistency.

3.2.Eigenenergies of the spin-S Heisenberg star
Let us now turn back to the spin-S Heisenberg star.Depending on whether S ≤l or S >l,the total angular momentum j of the star is accordingly determined by:


The eigenenergy for fixed l and j is

Similarly,the sub-ground state in the l-subspace with 0 ≤l <S is achieved for s=−l:
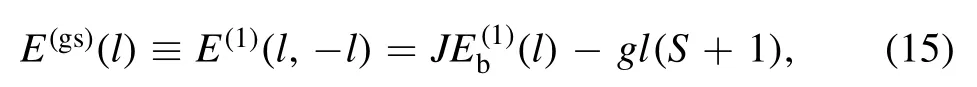
which is [2(S −l)+1]-fold degenerate.There exists a certain l=l<that minimizes E(gs)(l) for 0 ≤l <S.
Once E(gs)(l<) and E(gs)(l>) are obtained,the absolute ground state energy of H is simply
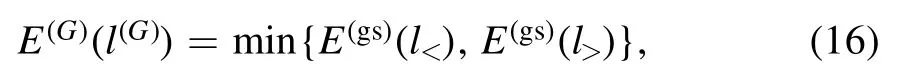
where l(G)is the total angular momentum of the bath in the global ground state.
The main panel of figure 2 shows the ground-state energy E(G)(l(G))as a function offor N=16 and S=1,2,…,7.We observe that:
(i) For fixedthe ground-state energy E(G)decreases with increasing S.In the largelimit,E(G)converges to the result of S=0 (or of a pure XXX chain) for different values of S.
(ii) For fixed S,E(G)is a nonmonotonic function ofindicating that there might exist level crossings at certain values of
(iii) In the smalllimit,E(G)increases linearly with increasingand the energy difference for adjacent S's is a constant.
The above behaviors of E(G)can be understood by inspecting equations (12) and (15).In the largelimit,the systembath coupling can be viewed as a perturbation for the XXX ring and the first terms in equations (12) and (15) are dominated,which explains the convergence of E(G)to the result for S=0.
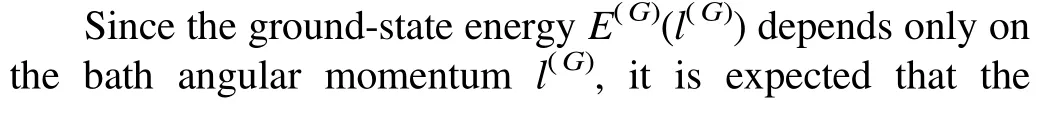
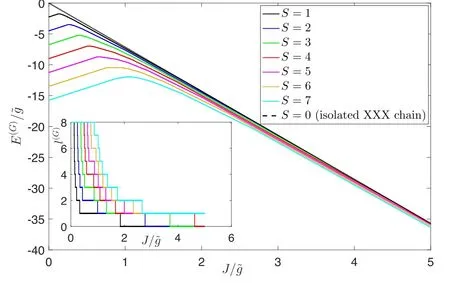
Figure 2.Main panel: the ground-state energyas a function of for a spin-S Heisenberg star with N=16 bath spins.Results for S=1,2,…,7 are shown.The dashed black line represents the result for a pure XXX chain or a Heisenberg star with S=0.Inset:the evolution of total angular momentum of the bath,l(G),asincreases.

3.3.Analytical results in the small J =~g limit


yielding the transition coupling strength

which is actually a linear function of S(inset of figure 2,the top horizontal lines).
4.Eigenstates
Let us now turn to study the eigenstates of the spin-S Heisenberg star.We first briefly describe how to obtain all the eigenstates of the Heisenberg star with the help the Bethe ansatz solution of the XXX chain,which divides the full Hilbert space into invariant subspaces of at most 2S+1 dimensions.We then focus on the sub-ground states within the sector with fixed l and derive closed-from expressions of these states in terms of the sub-ground states of the XXX chain in the l-sector.
4.1.General eigenstates: the Bethe ansatz method
We closely follow[13,22] to construct invariant subspaces of H based on the Bethe ansatz solution of the XXX bath HB.The Bethe states of HBwith M ≤N/2 spin flips are of the form

where{λj}are the Bethe roots determined by the Bethe ansatz equations,B(λi) is the spin-flipping operator appearing in the so-called monodromy matrix [22],and |F〉=|↑…↑〉 is the fully polarized reference state.
It is known that the Bethe state given by equation(22)is the highest weight state of the su(2)Lie algebra generated by the bath operators (L±,Lz).By successively applying the lowering operator L−to the Bethe states,we can obtain the (N −2M+1)-fold degenerate manifold corresponding to the eigenenergy EB(λ1,…,λM),which satisfies the Schrödinger equation HB|λ1,…,λM〉=EB(λ1,…,λM)|λ1,…,λM〉.Explicitly,we define [13]


Unlike the case of S=1/2 where |1/2〉|λ1,…,λM;n〉 and|−1/2〉|λ1,…,λM;n+1〉already form a closed subspace [13],for a general S ≤N/2 we need to further apply H to the newly generated states |Sm+1〉|λ1,…,λM;n −1〉 and |Sm−1〉|λ1,…,λM;n+1〉 to obtain a multi-dimensional invariant subspace.
For S ≤N/2,these invariant subspaces can be classified into three categories:
(I) For −S −N/2 ≤m ≤S −N/2 with m=Sm+n the total magnetization of the star,the configurations of(Sm,n)that conserve m are(−S,m+S),…,(m+N/2,−N/2).The dimension of the corresponding invariant subspace is therefore m+N/2+S+1 ≤2S+1.
(II) For S −N/2+1 ≤m ≤−S+N/2 −1,the configurations of(Sm,n)that conserve the total magnetization are(−S,m+S),…,(S,m −S).The dimension of the corresponding invariant subspace is 2S+1.
(III) For −S+N/2 ≤m ≤S+N/2,the configurations of(Sm,n) that conserve the total magnetization are(m −N/2,N/2),…,(S,m −S).The dimension of the corresponding invariant subspace is S −m+N/2+1 ≤2S+1.
In this way,the whole Hilbert space of the spin-S Heisenberg star is divided into invariant subspaces whose dimensions are at most 2S+1.In principle,we can numerically diagonalize the block Hamiltonians to obtain all the eigenstates and eigenenergies of the system.

It can be checked that N is identical to the total dimension of the Hilbert space (2S+1)2N.Below we focus on the subground states for fixed l's.As we will see,these sub-ground states admit closed-form expressions in terms of the subground states of the pure XXX ring.
4.2.Sub-ground states for S ≤l ≤

After a tedious but straightforward calculation,we arrive at the following unnormalized sub-ground state (see the appendix for the derivation)
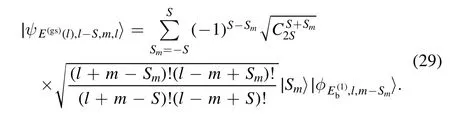

In particular,the highest-weight statecan be normalized as (see appendix)Note that the sub-ground states do not depend on the coupling strengths J and g but are determined by the quantum number l.
4.3.Sub-ground states for 0 ≤l
It can be similarly shown that [by making the substitutions S →l,l →S,Sm→lmin equation (29)]

5.Real-time dynamics
The spin-S Heisenberg star given by equation (1) is so special that it cannot generate any intrabath coupling-induced centralspin dynamics.Suppose χSis an arbitrary observable belonging to the central spin,its time evolution from an initial state|ψ(0)〉is given by


It is easy to see that including any central-spin term(such as a Zeeman term or a single-ion anisotropy,etc.) does not change the foregoing property,as has already been observed in the investigation of the central spin coherence from a pure state[13].Thus,to obtain nontrivial dynamics of the central spin induced by the intrabath coupling,one has to either include the thermal effect [13] or to go beyond the homogeneous systembath coupling or isotropic intrabath coupling [12].In spite of these facts,the dynamics of any bath operator ηBdepends on both J and g since generally[Hb,ηB]≠0 and
In this work,we first study the dynamics of the antiferromagnetic order in the XXX bath governed by the spin-S Heisenberg star H,with the XXX bath prepared in a Néel state.We then study the central spin dynamics in a slighted generalized Heisenberg star with intrabath anisotropy.To be specific,in this case,we choose the bath initial state as a spin coherent state.
5.1.Dynamics of antiferromagnetic order in the spin-S Heisenberg star
The dynamics of antiferromagnetic order in an XXZ bath with inhomogeneous system-bath coupling and anisotropic intrabath coupling have been thoroughly studied in a related work by the authors [12].Compare with the case of an isolated XXZ chain[14],it is found that both the system-bath coupling and the size of the central spin have significant influence on the relaxation of the antiferromagntic order.We show that some of the dynamical behaviors of the antiferromagnetic order observed in [12] for inhomogeneous system-bath couplings are still robust in the homogeneous Heisenberg star described by H.
We assume that the star is initially prepared in a product state
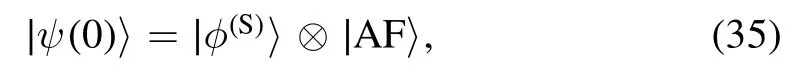
where |φ(S)〉 is the initial state of the central spin and the bath initial state is chosen as the Néel state |AF〉=|↓↑…↓↑〉.For arbitrary S <N/2,the dynamics of the spin-S Heisenberg star H are simulated by using an equations-of-motion method based on analytical expressions of spin-operator matrix elements for the XX chain [24],see [12] for details of the method.
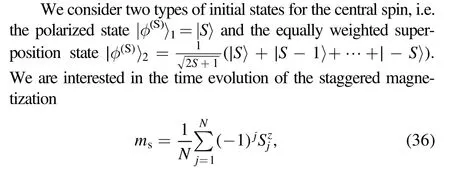
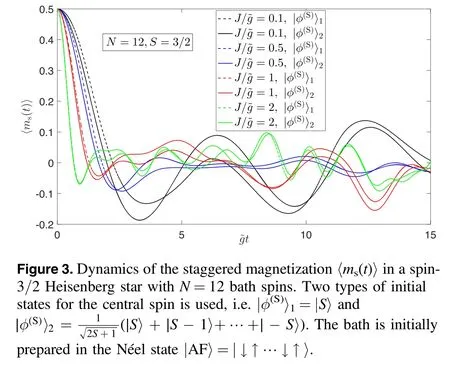
which is a measure of the antiferromagnetic order within the XXX bath.Figure 3 shows the staggered magnetization dynamics〈ms(t)〉for an XXX bath with N=12 sites and for a central spin of size S=3/2.For both types of the central-spin initial states|φ(S)〉1and|φ(S)〉2,we see that〈ms(t)〉decays more rapidly as the intrabath coupling J increases,which is consistent with the case of inhomogeneous system-bath couplings.Qualitatively,it is the nearest-neighbor intrabath coupling that mainly controls the shorttime dynamics of the staggered magnetization.
In figure 4 we plot 〈ms(t)〉 for different values of S and intrabath coupling J.Generally,a larger S induces a faster initial decay of〈ms(t)〉since there are 2S+1 channels for the central spin to interact with the XXX bath.This behavior is similar to that obtained for inhomogeneous system-bath couplings[12].As expected,the deviation in the dynamics for different S's becomes smaller when the intrabath coupling is large enough (lower panels of figure 4).

Figure 4.Dynamics of the staggered magnetization〈ms(t)〉in a spin-S Heisenberg star with N=12 bath spins.Results for S=1/2,1,and 3/2 are shown for fixed .The initial state of the central spin is chosen as|φ(S)〉1=|S〉and the bath is initially prepared in the Néel state |AF〉=|↓↑…↓↑〉.
5.2.Central spin dynamics in a modified Heisenberg star
The polarization dynamics of a qubit coupled to a noninteracting spin bath prepared in the spin coherent state have been studied in several previous works[15–17].However,the case of a larger central spin coupled to an interacting spin bath is less studied.In this subsection,we will study the polarization dynamics of the central spin when the bath is prepared in a spin coherent state.As mentioned above,to get nontrivial intrabath coupling-induced central spin dynamics,we have to slightly modify the Heisenberg star given by equation (1):
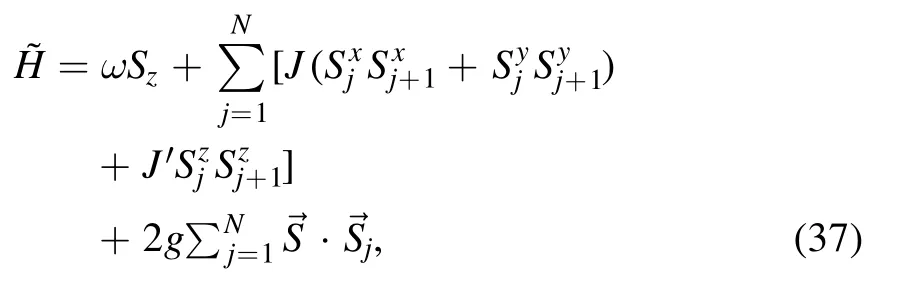
where ω is an external magnetic field,J andJ′are the in-plane and Ising parts of the intrabath coupling strength,respectively.Note that the bath angular momentumis no longer conserved forJ≠J′.ForJ=J′ and S=1/2,H˜is reduced to the model studied in [13],which conservesIf one further sets J=0,thenis reduced to a qubit−big-spin model [16],whose dynamics can be analytically solved by using either a recurrence method [16,23] or an interactionpicture method [17].
The initial state of the whole system reads

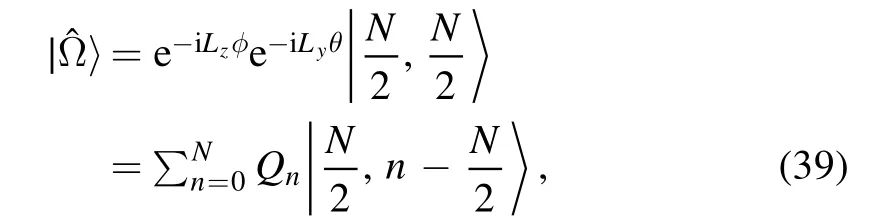
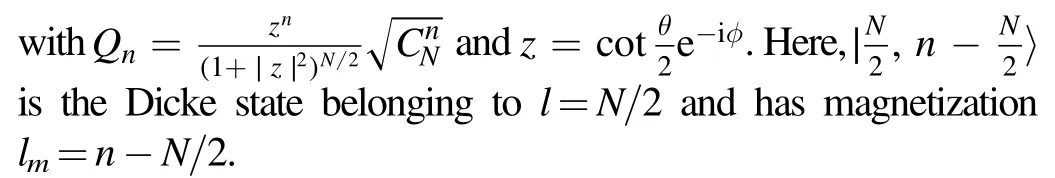
Let us first look at the case of an XXX bath withJ=J′.We have demonstrated that in this case,the central spin dynamics is independent of the value of J,which can be seen more straightforwardly by noting that the spin coherent stateis an eigenstate of JHbwith eigenvalue NJ/4:
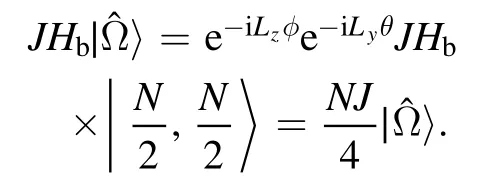
It is thus necessary to go beyond the isotropic pointJ=J′in order to observe nontrivial polarization dynamics induced by the intrabath coupling.Nevertheless,let us first study the effect of the value of S on the central spin polarization dynamics forJ=J′.
The top panel of figure 5 shows the polarization dynamics 〈Sz(t)〉/S of an S=1/2 central spin forJ=J′ and under the resonant condition ω=g [16].It can be seen that the polarization exhibits the so-called collapse-revival behavior and the revival peaks occur atgt≈mNπ(m∈ Z),recovering the analytical results presented in[16].The middle and bottom panels of figure 5 show 〈Sz(t)〉/S for S=1 and S=3/2,respectively.The polarization still shows collapses and revivals during the evolution,but with rich fine structures.For example,the initial revival region seems to show 2S discrete sub-peaks before the first collapse occurs.These structures reappear after the regular revival region consisting of 2S+1 packets.We note that similar polarization dynamics are observed in [23] for a spin-1 central spin homogeneously coupled to a noninteracting spin bath.
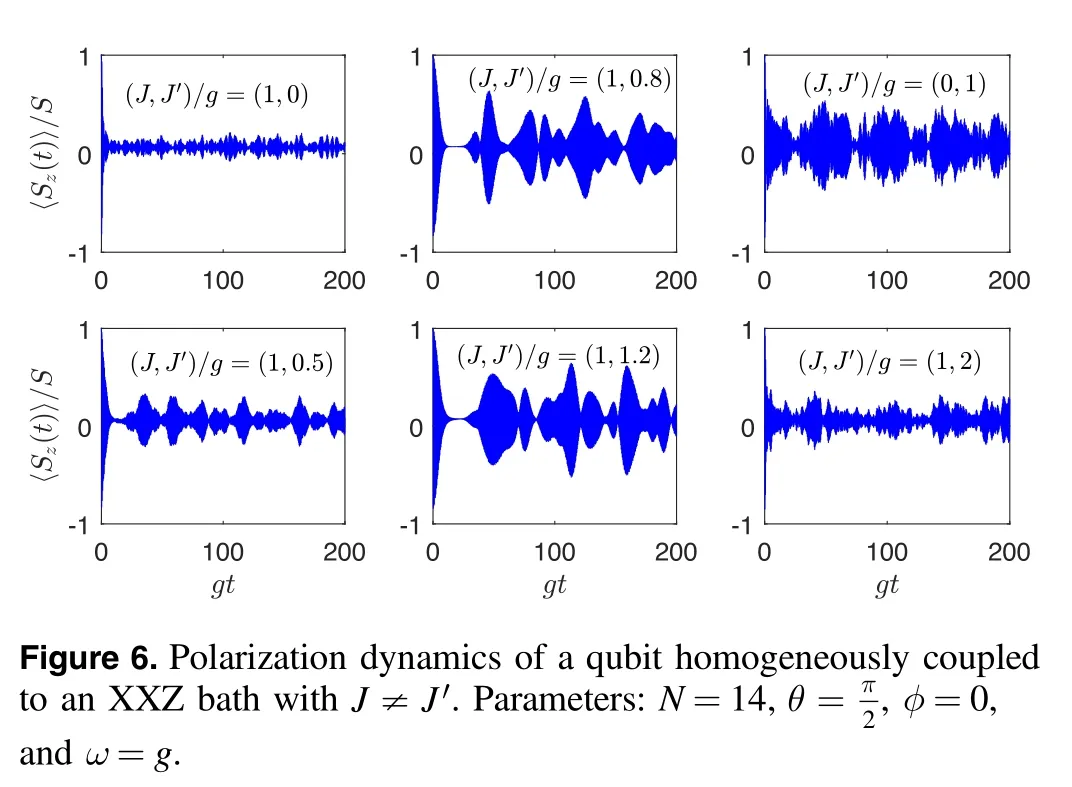
To see the effect of the anisotropy of the intrabath coupling on the polarization dynamics,we plot in figure 6〈Sz(t)〉/S for S=1/2 and several pairs of(Jg,J′g).It can be seen that the collapse-revival behaviors are generally destroyed,although for(J,J′)g= (1 ,0.8)and(1,1.2)there is some evidence of collapse (middle column of figure 6) at short time since they are close to the isotropic pointJ′J=1 .If we separate the termout of,it is easy to check that this term does not commute with the remaining part ofH˜.As a result,the dynamics depends not only onJ′ -Jbut also on J (right column of figure 6).Actually,since the termbreaks the conservation ofthe time-evolved state will run out of the l=N/2 subspace,making the collapse-revival phenomena fragile with respect to anisotropic intrabath coupling.

6.Conclusions
In this work,we generalize the spin-1/2 Heisenberg proposed by Richter and Voigt [10] to the case of arbitrary S <N/2.Compared with the spin-1/2 counterpart,both the groundstate and the dynamical behaviors are found to have richer structures.In principle,the eigenenergies and eigenstates of the system can be obtained by block diagonalizing the Hamiltonian using the Bethe ansatz solution of the XXX bath,yielding invariant subspaces whose dimensions do not exceed 2S+1.Based on the four conserved quantities of the model,we obtain all the eigenenergies of the model.The expressions of these eigenenergies differ depending on whether S is larger or smaller than the bath angular momentum l.The sub-ground state energies for fixed l depend only on the quantum number l.The evolutions of the ground-state energy and the associated bath angular momentum are numerically analyzed when the intrabath coupling J and the central-spin size S are varied.We explain the observed behaviors of these quantities in the weak and strong intrabath coupling limits.We also derive closed-form expressions for the degenerate sub-ground states in each l-subspace.
We then study the real-time dynamics of the spin-S Heisenberg star.Since the bath Hamiltonian commutes with the whole Hamiltonian,the intrabath coupling has no effect on the central spin dynamics if the system is prepared in a pure state.We thus turn to study the antiferromagnetic order dynamics within the XXX bath.Following [12],we set the bath initial state to be a Néel state and investigate how the staggered magnetization evolves under the combined influence of the intrabath coupling and the system-bath coupling.We study the effects of the central spin initial state,the central spin size,and the system-bath coupling strength on the staggered magnetization dynamics and find similar behaviors to the inhomogeneous coupling case[12].
We finally study the central-spin polarization for a bath prepared in a spin coherent state.This is motivated by several recent works in which the polarization dynamics of a spin-1/2 coupled to a noninteracting spin bath are thoroughly studied[15–17].To observe nontrivial polarization dynamics that depend on the intrabath coupling,we extend the spin-S Heisenberg star by including a Zeeman term of the central spin and the anisotropy in the intrabath coupling.At the isotropic point of the bath,we find that the polarization dynamics for S >1/2 exhibit collapse-revival behaviors with fine structures.However,for a spin bath with anisotropic coupling,the collapserevival phenomena are generally found to be destroyed.
As an exactly soluble model,there are some other aspects of the spin-S Heisenberg star that deserve further investigation.For example,it would be interesting to study the dynamics of entanglement and quantum Fisher information and to understand quantum metrology in the present model.The analytical calculation of spin correlations in the weak intrabath coupling limit should be appealing.These studies will be left for future work.
Acknowledgments
This work was supported by the National Key R&D Program of China under Grant No.2021YFA1400803 and by the Natural Science Foundation of China (NSFC) under Grant No.11 705 007.
Appendix.Derivation of equation (29)
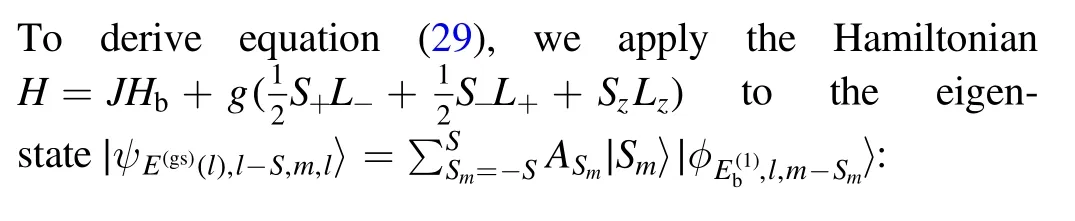

By comparing the coefficients on both sides,we get

Combining equations (47) with (48) gives
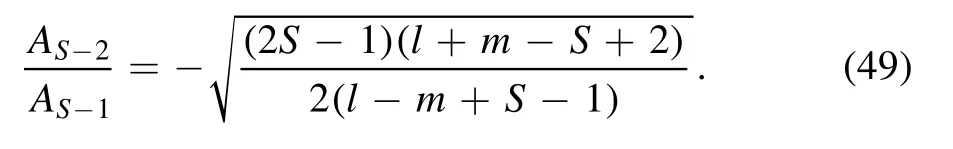
The forms of equations (47) and (49) suggest the following ansatz:
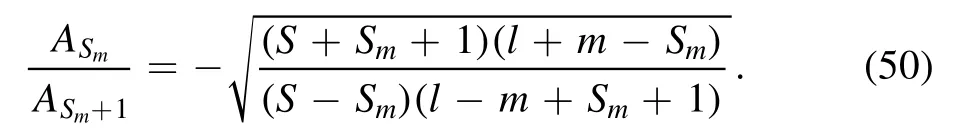
It is straightforward to verify that the above ansatz indeed solves equation (45) for all −S <Sm<S.
Starting with AS,we find after iteration
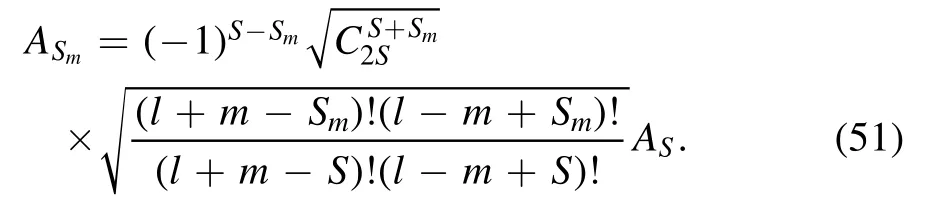
By inserting equation (51) into the wave function,we obtain the unnormalized sub-ground state given by equation (29) in the main text.
If we choose m=l −S,then
whose squared norm is
 Communications in Theoretical Physics2022年8期
Communications in Theoretical Physics2022年8期
- Communications in Theoretical Physics的其它文章
- Errata and Addendum: Magnetic properties of an antiferromagnetic spin-1/2 XYZ model in the presence of different magnetic fields:finite-size effects of inhomogeneity property(2019,Commun.Theor.Phys.71 1253–1260)
- The second harmonic generation in GaAs/GaAlAs spherical quantum dots under Woods-Saxon plus attractive inversely quadratic potential
- Toy model that explains the regulation of cholesterol on lipid rafts
- The ringing of quantum corrected Schwarzschild black hole with GUP
- Quantum corrections to the thermodynamics and phase transition of a black hole surrounded by a cavity in the extended phase space
- Swampland dS conjecture in mimetic f(R,T)gravity

It can be similarly shown that [by making the substitutions S →l,l →S,Sm→lmin equation (29)]

5.Real-time dynamics
The spin-S Heisenberg star given by equation (1) is so special that it cannot generate any intrabath coupling-induced centralspin dynamics.Suppose χSis an arbitrary observable belonging to the central spin,its time evolution from an initial state|ψ(0)〉is given by


It is easy to see that including any central-spin term(such as a Zeeman term or a single-ion anisotropy,etc.) does not change the foregoing property,as has already been observed in the investigation of the central spin coherence from a pure state[13].Thus,to obtain nontrivial dynamics of the central spin induced by the intrabath coupling,one has to either include the thermal effect [13] or to go beyond the homogeneous systembath coupling or isotropic intrabath coupling [12].In spite of these facts,the dynamics of any bath operator ηBdepends on both J and g since generally[Hb,ηB]≠0 and
In this work,we first study the dynamics of the antiferromagnetic order in the XXX bath governed by the spin-S Heisenberg star H,with the XXX bath prepared in a Néel state.We then study the central spin dynamics in a slighted generalized Heisenberg star with intrabath anisotropy.To be specific,in this case,we choose the bath initial state as a spin coherent state.

5.1.Dynamics of antiferromagnetic order in the spin-S Heisenberg star
The dynamics of antiferromagnetic order in an XXZ bath with inhomogeneous system-bath coupling and anisotropic intrabath coupling have been thoroughly studied in a related work by the authors [12].Compare with the case of an isolated XXZ chain[14],it is found that both the system-bath coupling and the size of the central spin have significant influence on the relaxation of the antiferromagntic order.We show that some of the dynamical behaviors of the antiferromagnetic order observed in [12] for inhomogeneous system-bath couplings are still robust in the homogeneous Heisenberg star described by H.
We assume that the star is initially prepared in a product state
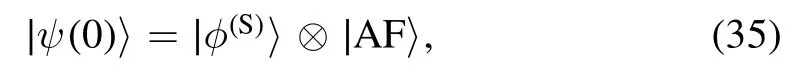
where |φ(S)〉 is the initial state of the central spin and the bath initial state is chosen as the Néel state |AF〉=|↓↑…↓↑〉.For arbitrary S <N/2,the dynamics of the spin-S Heisenberg star H are simulated by using an equations-of-motion method based on analytical expressions of spin-operator matrix elements for the XX chain [24],see [12] for details of the method.
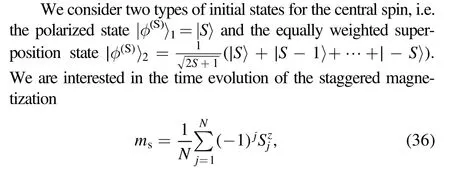
which is a measure of the antiferromagnetic order within the XXX bath.Figure 3 shows the staggered magnetization dynamics〈ms(t)〉for an XXX bath with N=12 sites and for a central spin of size S=3/2.For both types of the central-spin initial states|φ(S)〉1and|φ(S)〉2,we see that〈ms(t)〉decays more rapidly as the intrabath coupling J increases,which is consistent with the case of inhomogeneous system-bath couplings.Qualitatively,it is the nearest-neighbor intrabath coupling that mainly controls the shorttime dynamics of the staggered magnetization.
In figure 4 we plot 〈ms(t)〉 for different values of S and intrabath coupling J.Generally,a larger S induces a faster initial decay of〈ms(t)〉since there are 2S+1 channels for the central spin to interact with the XXX bath.This behavior is similar to that obtained for inhomogeneous system-bath couplings[12].As expected,the deviation in the dynamics for different S's becomes smaller when the intrabath coupling is large enough (lower panels of figure 4).

Figure 4.Dynamics of the staggered magnetization〈ms(t)〉in a spin-S Heisenberg star with N=12 bath spins.Results for S=1/2,1,and 3/2 are shown for fixed .The initial state of the central spin is chosen as|φ(S)〉1=|S〉and the bath is initially prepared in the Néel state |AF〉=|↓↑…↓↑〉.
5.2.Central spin dynamics in a modified Heisenberg star
The polarization dynamics of a qubit coupled to a noninteracting spin bath prepared in the spin coherent state have been studied in several previous works[15–17].However,the case of a larger central spin coupled to an interacting spin bath is less studied.In this subsection,we will study the polarization dynamics of the central spin when the bath is prepared in a spin coherent state.As mentioned above,to get nontrivial intrabath coupling-induced central spin dynamics,we have to slightly modify the Heisenberg star given by equation (1):
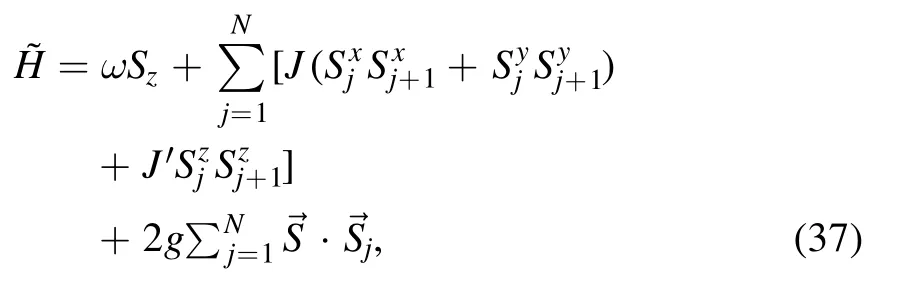
where ω is an external magnetic field,J andJ′are the in-plane and Ising parts of the intrabath coupling strength,respectively.Note that the bath angular momentumis no longer conserved forJ≠J′.ForJ=J′ and S=1/2,H˜is reduced to the model studied in [13],which conservesIf one further sets J=0,thenis reduced to a qubit−big-spin model [16],whose dynamics can be analytically solved by using either a recurrence method [16,23] or an interactionpicture method [17].
The initial state of the whole system reads

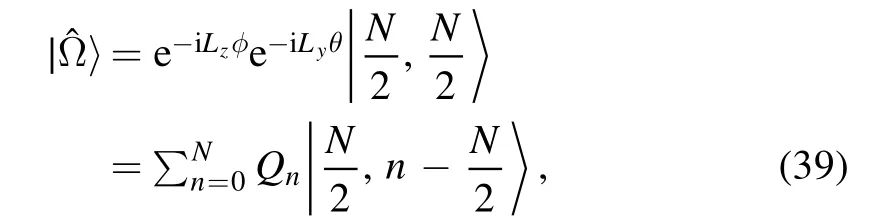
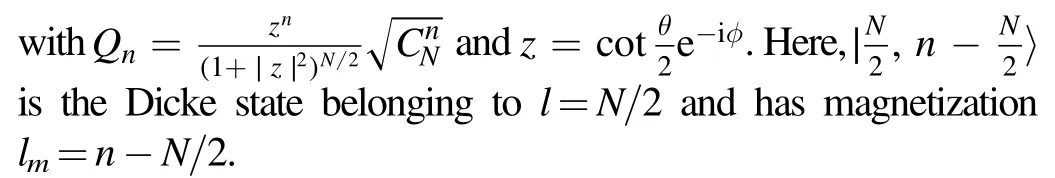
Let us first look at the case of an XXX bath withJ=J′.We have demonstrated that in this case,the central spin dynamics is independent of the value of J,which can be seen more straightforwardly by noting that the spin coherent stateis an eigenstate of JHbwith eigenvalue NJ/4:
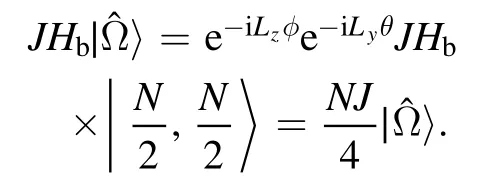
It is thus necessary to go beyond the isotropic pointJ=J′in order to observe nontrivial polarization dynamics induced by the intrabath coupling.Nevertheless,let us first study the effect of the value of S on the central spin polarization dynamics forJ=J′.
The top panel of figure 5 shows the polarization dynamics 〈Sz(t)〉/S of an S=1/2 central spin forJ=J′ and under the resonant condition ω=g [16].It can be seen that the polarization exhibits the so-called collapse-revival behavior and the revival peaks occur atgt≈mNπ(m∈ Z),recovering the analytical results presented in[16].The middle and bottom panels of figure 5 show 〈Sz(t)〉/S for S=1 and S=3/2,respectively.The polarization still shows collapses and revivals during the evolution,but with rich fine structures.For example,the initial revival region seems to show 2S discrete sub-peaks before the first collapse occurs.These structures reappear after the regular revival region consisting of 2S+1 packets.We note that similar polarization dynamics are observed in [23] for a spin-1 central spin homogeneously coupled to a noninteracting spin bath.
To see the effect of the anisotropy of the intrabath coupling on the polarization dynamics,we plot in figure 6〈Sz(t)〉/S for S=1/2 and several pairs of(Jg,J′g).It can be seen that the collapse-revival behaviors are generally destroyed,although for(J,J′)g= (1 ,0.8)and(1,1.2)there is some evidence of collapse (middle column of figure 6) at short time since they are close to the isotropic pointJ′J=1 .If we separate the termout of,it is easy to check that this term does not commute with the remaining part ofH˜.As a result,the dynamics depends not only onJ′ -Jbut also on J (right column of figure 6).Actually,since the termbreaks the conservation ofthe time-evolved state will run out of the l=N/2 subspace,making the collapse-revival phenomena fragile with respect to anisotropic intrabath coupling.


6.Conclusions
In this work,we generalize the spin-1/2 Heisenberg proposed by Richter and Voigt [10] to the case of arbitrary S <N/2.Compared with the spin-1/2 counterpart,both the groundstate and the dynamical behaviors are found to have richer structures.In principle,the eigenenergies and eigenstates of the system can be obtained by block diagonalizing the Hamiltonian using the Bethe ansatz solution of the XXX bath,yielding invariant subspaces whose dimensions do not exceed 2S+1.Based on the four conserved quantities of the model,we obtain all the eigenenergies of the model.The expressions of these eigenenergies differ depending on whether S is larger or smaller than the bath angular momentum l.The sub-ground state energies for fixed l depend only on the quantum number l.The evolutions of the ground-state energy and the associated bath angular momentum are numerically analyzed when the intrabath coupling J and the central-spin size S are varied.We explain the observed behaviors of these quantities in the weak and strong intrabath coupling limits.We also derive closed-form expressions for the degenerate sub-ground states in each l-subspace.
We then study the real-time dynamics of the spin-S Heisenberg star.Since the bath Hamiltonian commutes with the whole Hamiltonian,the intrabath coupling has no effect on the central spin dynamics if the system is prepared in a pure state.We thus turn to study the antiferromagnetic order dynamics within the XXX bath.Following [12],we set the bath initial state to be a Néel state and investigate how the staggered magnetization evolves under the combined influence of the intrabath coupling and the system-bath coupling.We study the effects of the central spin initial state,the central spin size,and the system-bath coupling strength on the staggered magnetization dynamics and find similar behaviors to the inhomogeneous coupling case[12].
We finally study the central-spin polarization for a bath prepared in a spin coherent state.This is motivated by several recent works in which the polarization dynamics of a spin-1/2 coupled to a noninteracting spin bath are thoroughly studied[15–17].To observe nontrivial polarization dynamics that depend on the intrabath coupling,we extend the spin-S Heisenberg star by including a Zeeman term of the central spin and the anisotropy in the intrabath coupling.At the isotropic point of the bath,we find that the polarization dynamics for S >1/2 exhibit collapse-revival behaviors with fine structures.However,for a spin bath with anisotropic coupling,the collapserevival phenomena are generally found to be destroyed.
As an exactly soluble model,there are some other aspects of the spin-S Heisenberg star that deserve further investigation.For example,it would be interesting to study the dynamics of entanglement and quantum Fisher information and to understand quantum metrology in the present model.The analytical calculation of spin correlations in the weak intrabath coupling limit should be appealing.These studies will be left for future work.
Acknowledgments
This work was supported by the National Key R&D Program of China under Grant No.2021YFA1400803 and by the Natural Science Foundation of China (NSFC) under Grant No.11 705 007.
Appendix.Derivation of equation (29)
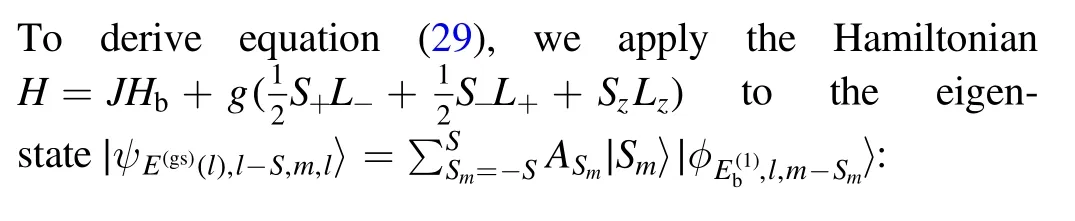

By comparing the coefficients on both sides,we get

Combining equations (47) with (48) gives
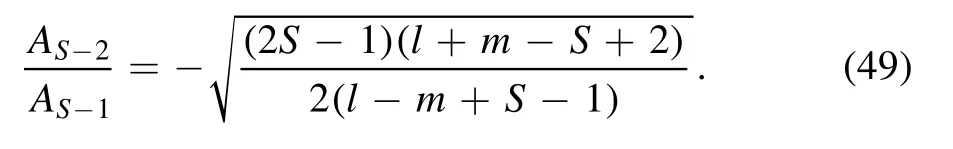
The forms of equations (47) and (49) suggest the following ansatz:
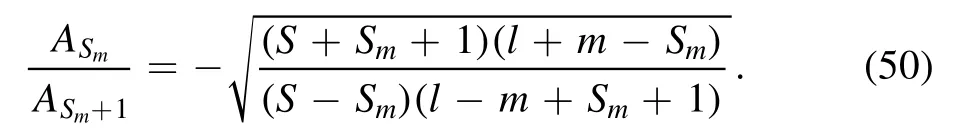
It is straightforward to verify that the above ansatz indeed solves equation (45) for all −S <Sm<S.
Starting with AS,we find after iteration
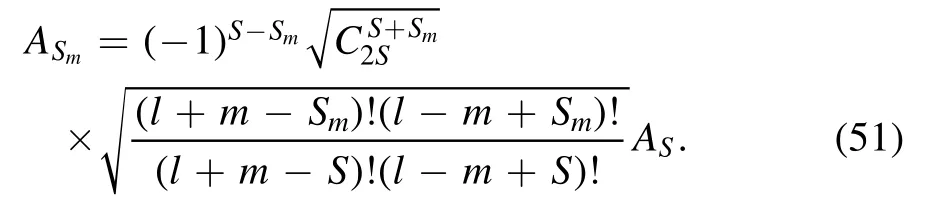
By inserting equation (51) into the wave function,we obtain the unnormalized sub-ground state given by equation (29) in the main text.
If we choose m=l −S,then
whose squared norm is
 Communications in Theoretical Physics2022年8期
Communications in Theoretical Physics2022年8期
- Communications in Theoretical Physics的其它文章
- Errata and Addendum: Magnetic properties of an antiferromagnetic spin-1/2 XYZ model in the presence of different magnetic fields:finite-size effects of inhomogeneity property(2019,Commun.Theor.Phys.71 1253–1260)
- The second harmonic generation in GaAs/GaAlAs spherical quantum dots under Woods-Saxon plus attractive inversely quadratic potential
- Toy model that explains the regulation of cholesterol on lipid rafts
- The ringing of quantum corrected Schwarzschild black hole with GUP
- Quantum corrections to the thermodynamics and phase transition of a black hole surrounded by a cavity in the extended phase space
- Swampland dS conjecture in mimetic f(R,T)gravity
