Consistent Burgers equation expansion method and its applications to highdimensional Burgers-type equations

Gangwei Wang，Li Li and A H Kara

1 School of Mathematics and Statistics，Hebei University of Economics and Business，Shijiazhuang 050061，China

2 Library，Hebei University of Economics and Business，Shijiazhuang 050061，China

3 School of Mathematics，University of the Witwatersrand，Private Bag 3，Wits 2050，Johannesburg，South Africa

Abstract

Keywords: Burgers-type equations，consistent Burgers equation expansion (CBEE) method，CBEE solvability，explicit solutions

1.lntroduction

Nonlinear evolution equations (NLEEs) play an important role in many fields [1–9]，they come up in various science fields，such as nonlinear optics，fluid mechanics，plasma physics，condensed matter physics，biophysics，etc.It is well known that NLEEs is an important part of applied mathematics and mathematical physics.In recent years，a great many of authors have made many contributions in NLEEs from different aspects，which has promoted their development.Especially in recent decades，with the rapid development of mathematical physics and computer science，the subject has developed more rapidly and achieved more results.

Due to the complexity of NLEEs，in general，a large number of existing important NLEEs，are not easy to find analytical solutions.Even if one can find some exact solutions，it requires some skill.Besides，new solutions with physical significance need to be further constructed and discovered.Through the continuous efforts of mathematicians and physicists，a large number of effective methods have been established and developed，for example，the symmetry method[5–16]，inverse scattering transformation [1]，Ba¨cklund transformation [17，18]，Darboux transformations [19]，the Hirotas bilinear direct method [20]，auxiliary equation expansion method [21]，generalized multi-symplectic method [22–25]homogeneous balance method[26]，F-expansion method [27]，homotopy perturbation method[28，29]，CKs direct symmetry reduction method [30]，consistent Riccati expansion method[31]，consistent KdV expansion method [32] and so on.

Motivated by these papers，we propose a new approach，named as consistent Burgers equation expansion (CBEE)method to solve the NLEEs.On the basis of the (CBEE)method，NLEEs can be said to be CBEE solvable if it satisfies the CBEE.

As mentioned earlier，the exact solution of NLEE plays a very important role in explaining complex nonlinear phenomena.In addition to some methods mentioned in the previous references and the references cited therein，it is necessary to find new methods to solve NLEEs through appropriate skills or transformations.In the present paper，we found such a transformation，which directly converts complex research objects into simple classical research objects.For the high-dimensional Burgers equation，we can directly use this method to get their new solutions.In this way，the calculation is greatly simplified.Because compared with high-dimensional and high-order NLEEs，low-dimensional and low-order ones are easier to study.Therefore，not only the calculation is simplified，but also new solutions are obtained.In a word，the advantage of this method is that as long as we study the(1+1)-dimensional Burgers equation，we can get new solutions of high-dimensional burgers and other NLEEs.

The present paper is divided into the following parts.In section 2，the basic idea and steps of CBEE and some conceptions are given.In section 3，the application of this method to the (2+1)-dimensional Burgers equation is described systematically.Symmetries and conservation laws are presented in section 4.A brief summary and discussion are presented in the last section.

2.Basic definition of CBEE method and CBEE solvability of NLEEs

In the present section，we give some definitions and concepts of the CBBE and the CBEE solvability.Consider the NLEEs as follows

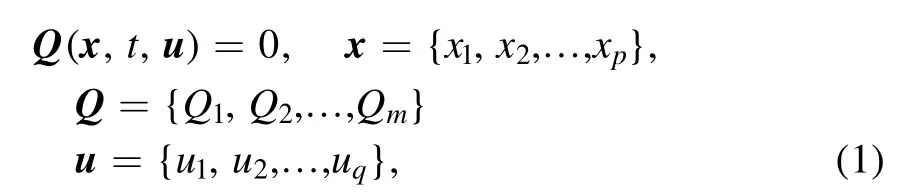
while Q is polynomial of functions uiand its derivatives term.In order to achieve this goal，we try to expand equation(1)in the following form

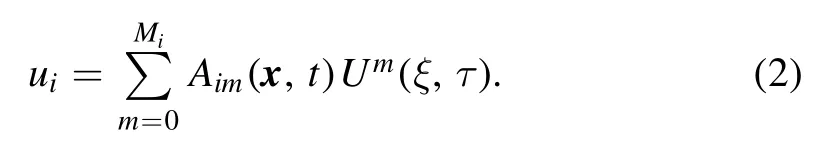
The positive integers Mi，i=1，2，...，q should be fixed via the leading order analysis from equation (1).In general，the function U(ξ，τ)is a special known function.Here we require that U(ξ，τ) satisfied the following famous Burgers equation[33]

Inserting equation (2) into equation (1) and using equation (3)，it should get

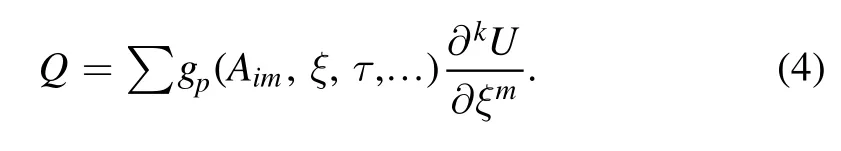
In general，as the number of equations is greater than the number of unknown variables，determining equation (5) is overdetermined.Solving them，we should obtain Aij，ξ，τ.Therefore，some new explicit solutions are presented via the Burgers equation.From the above analysis，we give the following statement:

Definition 1.The expansion (2) is a ‘CBEE’ and the NLEEs(1) is ‘CBEE solvable’，if system (5) is consistent.

3.CBEE solvability and novel explicit solutions of the (2+1)-dimensional Burgers equation

Through the analysis in the previous section，in order to prove the effectiveness of our proposed method，we consider the following (2+1)-dimensional Burgers equation [34–38]

This equation describes weakly nonlinear (1+2)-dimensional shocks which appear in dissipative media.With regard to more descriptions of this equation and its applications，see[34–38] and references therein.

Based on the steps of CBEE，by the leading order analysis of equation (6)，consider the following transformation

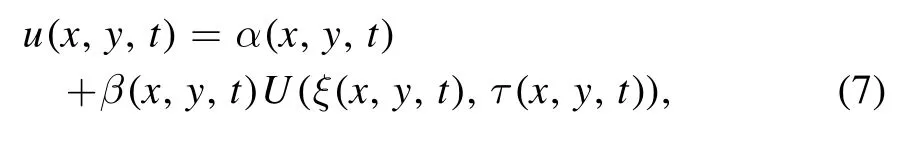
where α(x，y，y)，β(x，y，t)，ξ(x，y，t)，τ(x，y，t)are needed to be fixed later.HereU(ξ，τ) satisfies the Burgers equation(3)，that is to say，U(ξ，τ)is the solution of the Burgers equation (3).

Putting equation (7) into (6) and using equation (3)，we get some overdetermined partial differential equations(PDEs)with regard to α，β，ξ，τ.Let the coefficients of U and its different derivatives of U be equal to 0，one should obtain

where a，d，g，h are arbitrary functions of t，c1is an integral constant.

From the above analysis，in short，the(2+1)-dimensional Burgers equation(6)is CBEE solvable.Therefore，we get the following statement

Theorem 1.IfU(ξ，τ)is a solution of the Burgers equation (3)，then

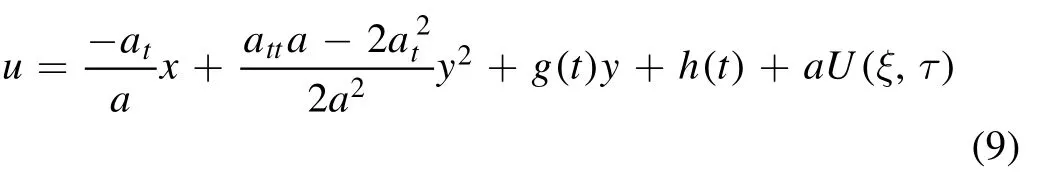
is a solution of the (2+1)-dimensional Burgers equation (6).Hereξ，τare given by equation (8).

Next，from the existing literature，we give some new solutions of the (2+1)-dimensional Burgers equation (6).In paper [38]，the authors give some explicit solutions of the(1+1)-dimensional Burgers equation (3)

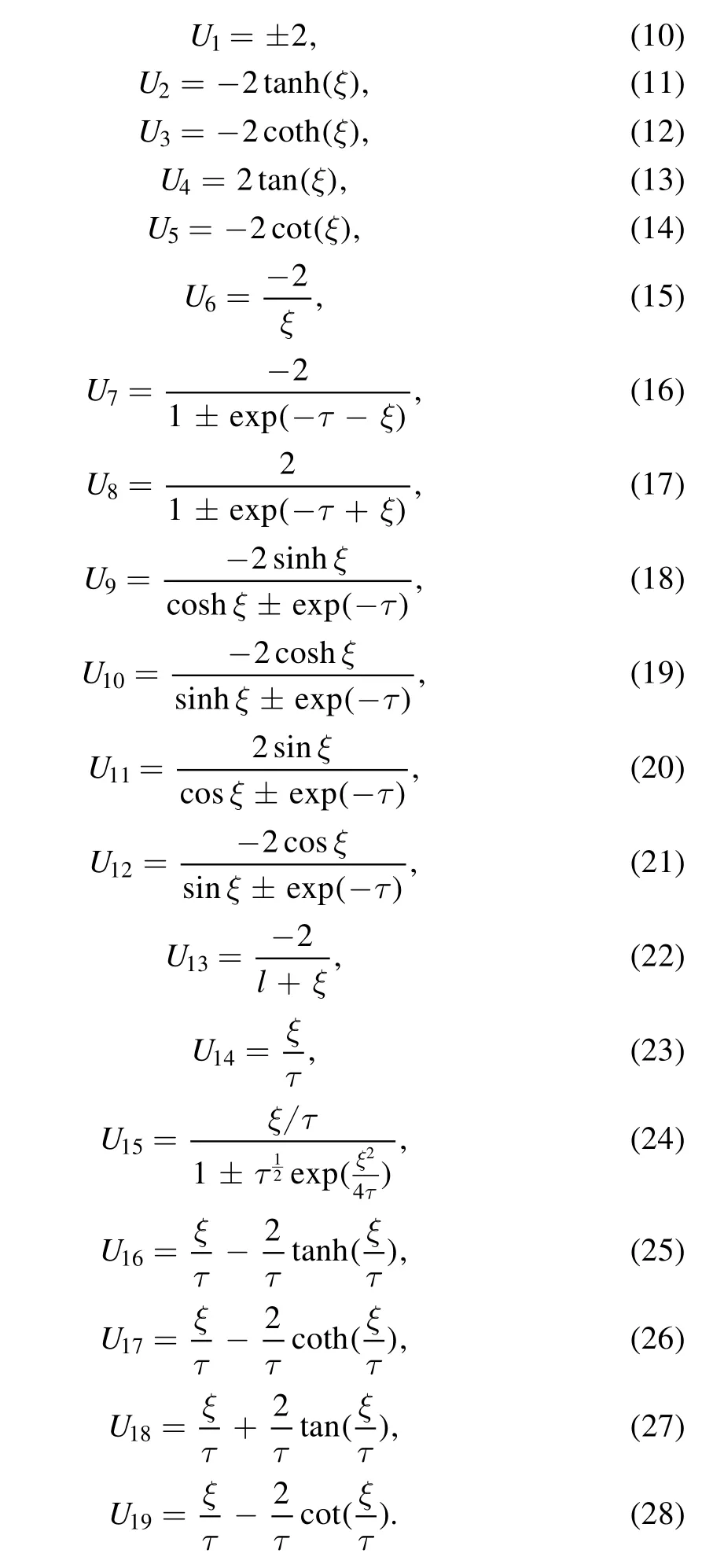
Therefore，based on the theorem(1)，we get new explicit solutions of the (2+1)-dimensional Burgers equation as follows:

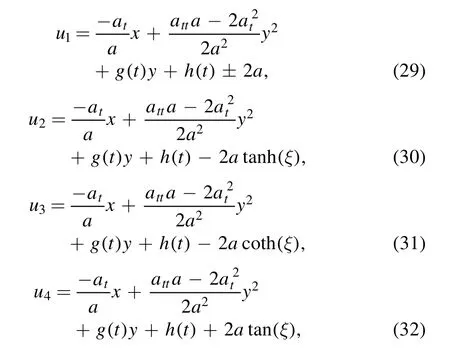
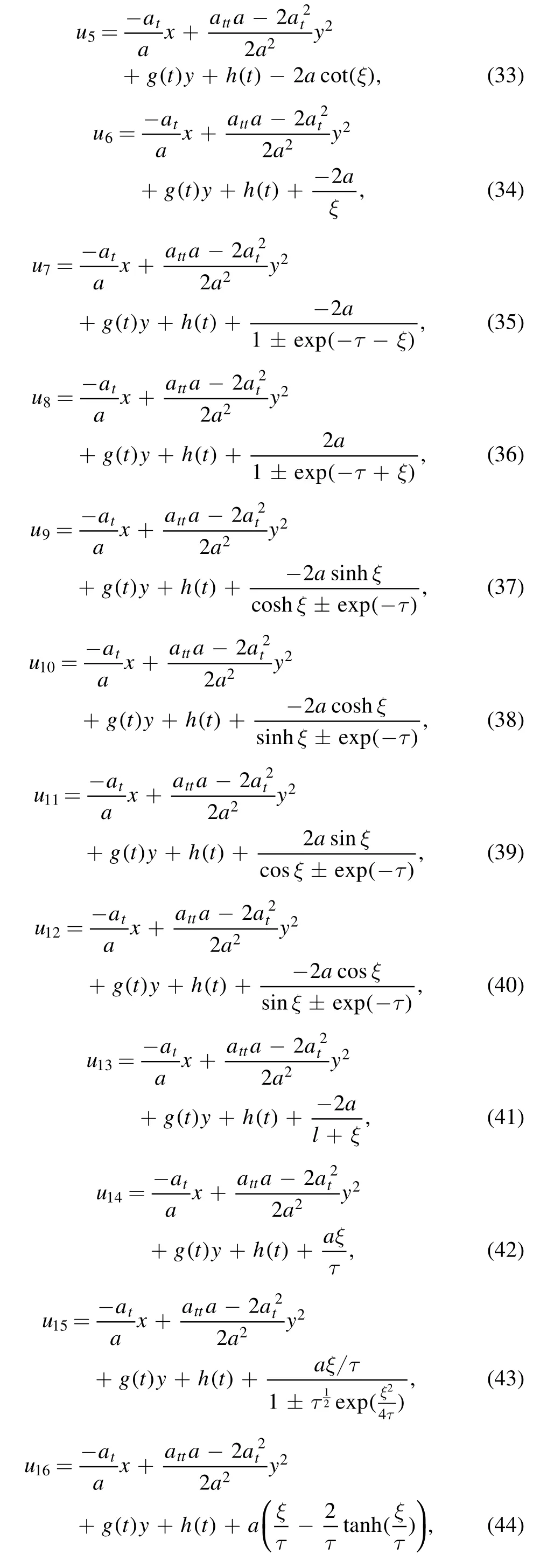
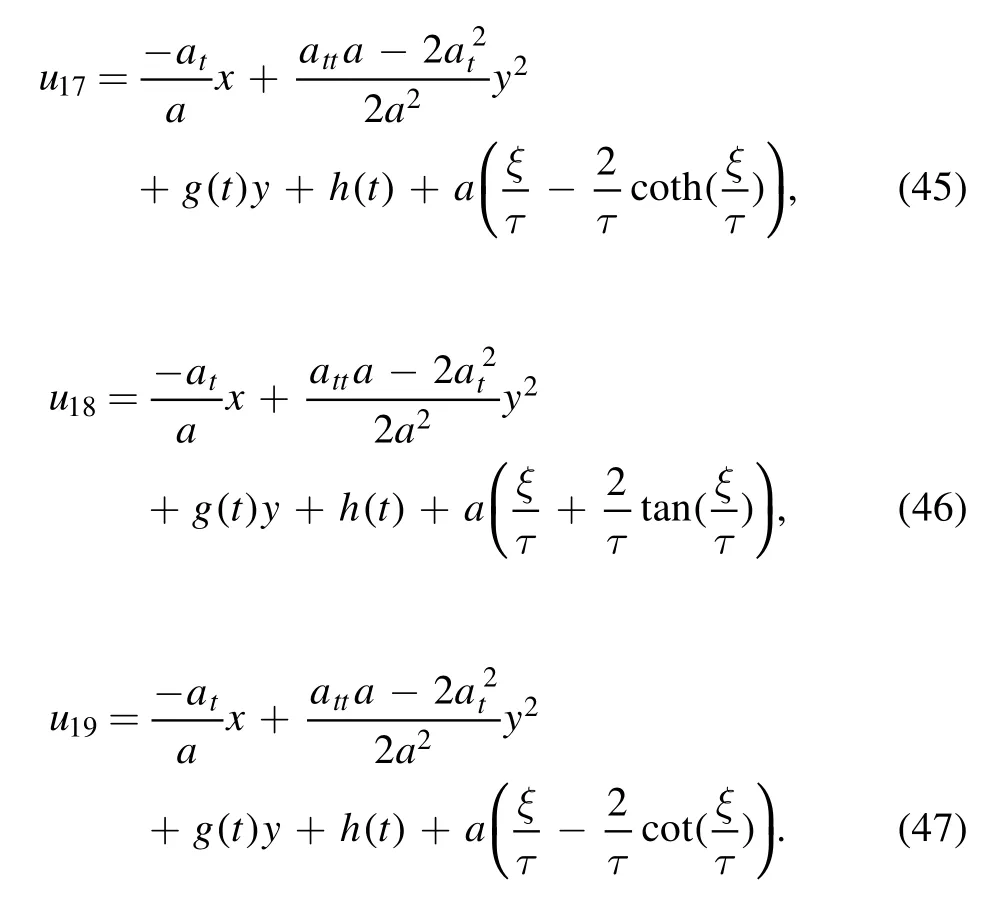
4.Symmetries and conservation laws

A nontrivial conservation law of equation (6) exists if there exists a vector (Tt，Tx，Ty) whose divergence

vanishes on the solutions of the PDE equation (6).We adopt the ‘multiplier approach’ [39] to construct the conserved flows where，by multipliers，we mean the differential functions Q(x，y，t，u，ux，…，uxx，…)such that the Euler–Lagrange operator (variational derivative) on

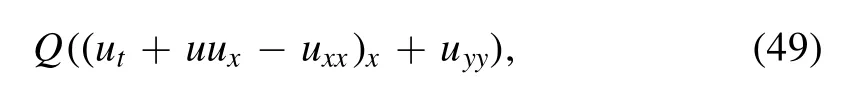
vanishes;each，such Q leads to a conserved flow.It turns out that for Q up to second-order in derivatives，we obtain only derivative independent，infinitely many forms for Q，viz.，

The conserved flow may then be determined by a homotopy formula [40] or by substituting into the definition (48).We state some special cases.

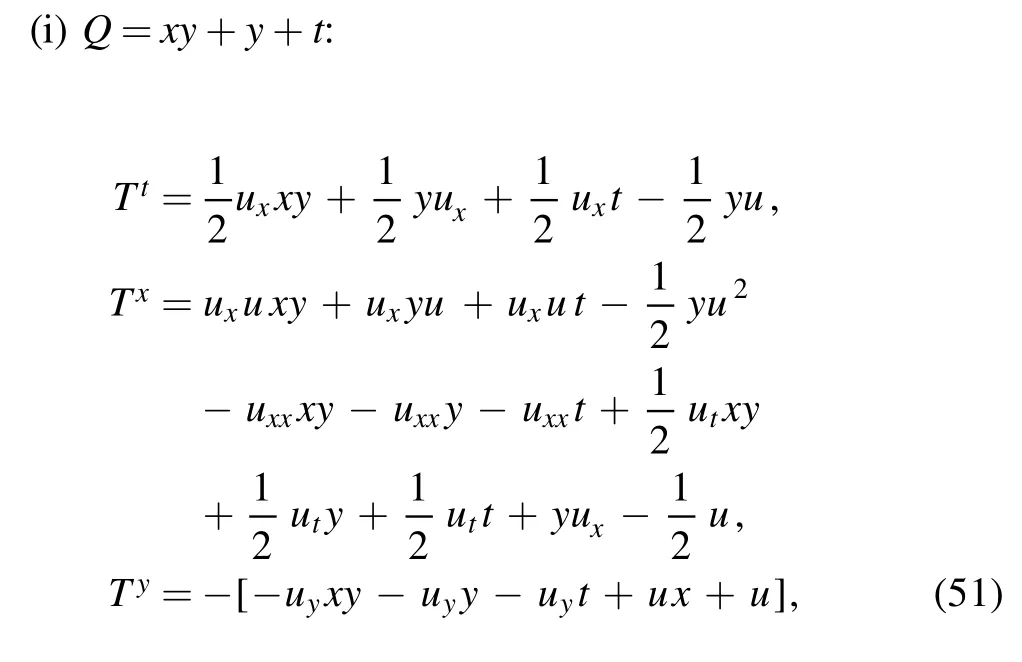
On the basis of the group method [5，7]，for a oneparameter group of infinitesimal transformation

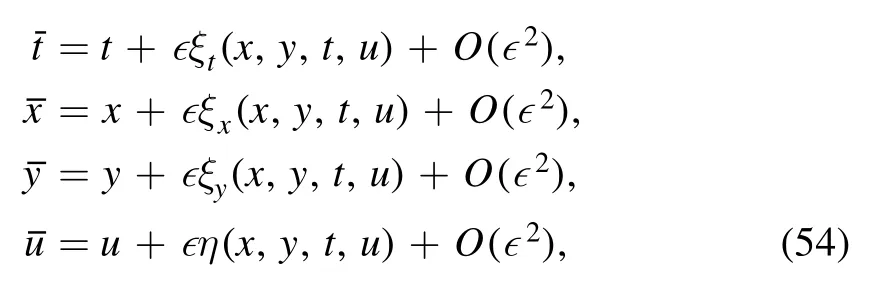
where ∈is a group parameter.The corresponding vector field is given by

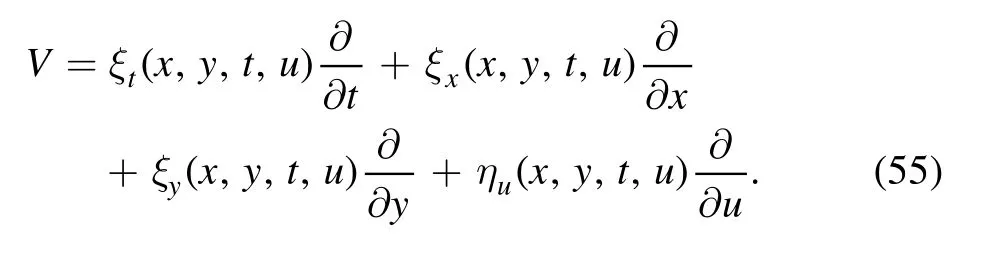
As this equation is second order，to solve this equation，the second prolongation Pr(2)V is required.Meanwhile，the invariant condition is given by:

where the total derivative operators is showed

Dx，Dt，Dyare functions of x，y and t，respectively.

The Lie point symmetry generators，as would be expected，also form an infinite algebra generated by the vector field

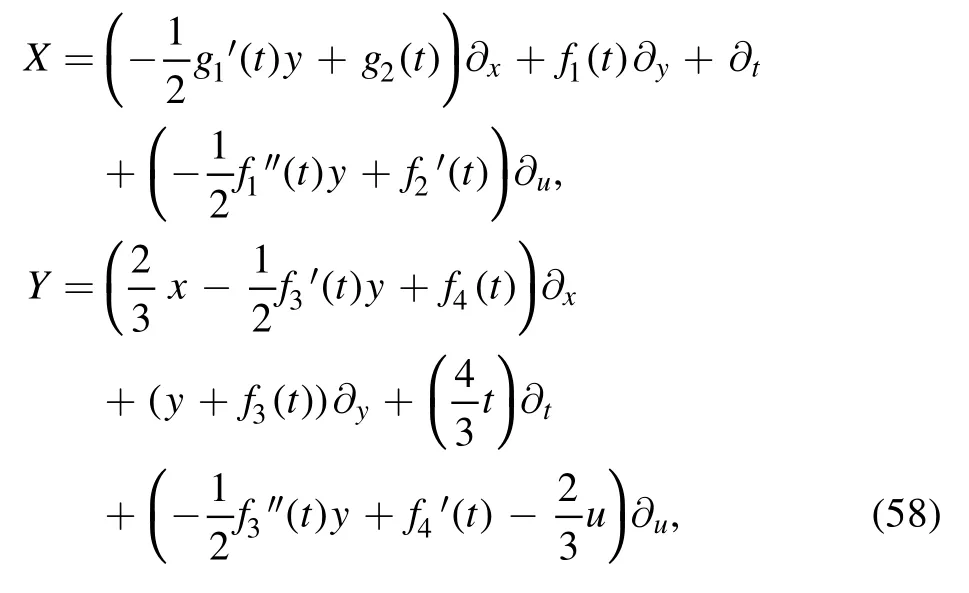
from which we may conclude some ‘polynomial’ generators

The variety of solutions obtained above may be attributed to the richness of the symmetries and conservation laws obtained here.

5.Conclusions

In the present paper，on the basis of the (1+1)-dimensional Burgers equation，we have proposed a simple，direct，and efficient method，named as CBEE method，for solving NLEEs.The convenience，simplicity and effectiveness of the method is illustrated by solving the (2+1)-dimensional Burgers equation.The main results in the present paper map solutions of the(1+1)-dimensional Burgers equation onto the(2+1)-dimensional Burgers equation.By choosing appropriate parameters，the transformation yields new solutions for the(2+1)-dimensional Burgers equation.Although not all the NLEEs are CBEE solvable，it is may shed further light on the solutions of some high-dimensional NLEEs.

Also，we note that a variety of solutions were obtained above and this can be predicted and attributed to the large number of symmetries and conservation laws that the PDE under investigation generated.

It is should be noted that this method，of course，should also be easily extended to other more (2+1)-dimensional，(3+1)-dimensional，and even more high-dimensional NLEEs.The method，in this paper，might become a useful，promising and powerful technique for solving other NLEEs.

Acknowledgments

We are very grateful to the editors and reviewers for their comments，which greatly improved the quality of this article.This work is supported by Natural Science Foundation of Hebei Province，China (No.A2018207030)，Youth Key Program of Hebei University of Economics and Business(2018QZ07)，Key Program of Hebei University of Economics and Business(2020ZD11)，Youth Team Support Program of Hebei University of Economics and Business，Study on system dynamics of scientific and technological innovation promoting the expansion and quality of residents’ consumption in Hebei Province(20556201D)，Youth Top-notch Talent Support Program of Higher Education of Hebei Province of China (BJ2020011).