The unified transform method to the highorder nonlinear Schrödinger equation with periodic initial condition

Leilei Liu，Weiguo Zhang，Jian Xu and Yuli Guo

College of Science，University of Shanghai for Science and Technology，China

Abstract In this paper，we study the high-order nonlinear Schrödinger equation with periodic initial conditions via the unified transform method extended by Fokas and Lenells.For the high-order nonlinear Schrödinger equation，the initial value problem on the circle can be expressed in terms of the solution of a Riemann–Hilbert problem.The related jump matrix can be explicitly expressed based on the initial data alone.Furthermore，we present the explicit solution，which corresponds to a one-gap solution.

Keywords: periodic initial condition，high-order nonlinear Schrödinger equation，unified transform method，Riemann–Hilbert problem

1.lntroduction

For nonlinear partial differential equations，solutions of spatial infinite decay and spatially periodic solutions are the two most widely studied classes of solutions.In the first of these classes，solutions of the initial value problem of integrable evolution equations can be solved by linear operations [1].To be precise，the inverse scatter transform，which was introduced about half a century ago，solved this problem groundbreakingly [2–6].

For the above-mentioned second classes-the spatially periodic solution，the finite gap integration method was introduced in the 1970s [7].Considering rational combinations of theta functions，which are defined on Riemann surfaces that the number of branch cuts is finite，the approach generates exact solutions named finite-gap solutions.If the given initial data belongs to the finite gap class，according to the Jacobian inversion problem on the finite Riemann surface，we can retrieve the solution of the initial value problem.But nevertheless，if the initial data does not belong to the finite gap potential energy category，then an additional theory is needed.Although the method can be extended to infinite Riemann surfaces [8–10]，the solutions of the Jacobian inversion problems on infinite surfaces are quite complicated.In fact，solutions with finite gaps are not easy to obtain computationally [2，11].

In 1997，Fokas proposed a novel method called the unified transform method (UTM) for solving the initial boundary value problem of integrable systems [12，13].The initial boundary value problems of many integrable equations have been studied，such as the nonlinear Schrödinger equation，sine-Gordon equation，and the mKdV equation[14–19].In 2013，Lenells generalized the UTM to the initial boundary value problem of an integrable system with pairs of third-order matrices Lax on the half-line [20].In 2014，Fan Engui and Xu Jian applied the UTM to the initial boundary value problem on the half-line of the Sasa-Satsuma equation and three-wave equation [21，22].Recently，Yan Zhenya extended the UTM to the fourth-order matrix spectral problem [23].

In 2004，Fokas and Its realized the UTM to the nonlinear Schrödinger equation on the finite interval [24].They show the solution of the nonlinear Schrödinger equation can be obtained by the related Riemann–Hilbert problem involving spectral functions defined in terms of initial datum and boundary values.Facts have proved that the boundary conditions，which correspond to the x-periodic problem，are linearizable.Recently，using the NLS equation as an example，Fokas and Lenells proposed a new method based on the unified transform to obtain the solution of the NLS equation with periodic initial conditions [25，26].Their method provides a new perspective on the initial value problem on the

Commun.Theor.Phys.74 (2022) 085001 (10pp)

https://doi.org/10.1088/1572-9494/ac7a23 circle，and creatively they get the expression of the solution of a Riemann–Hilbert problem only involving the initial data.

For the inverse scattering method，the unified transformation method is a generalization of the initial value problem to the initial boundary value problem.Through the simultaneous spectral analysis of the x-part and the t-part of the Lax pair，the solution of the initial boundary value problem of the integrable equation can be represented by the solution of the matrix RH problem on the complex plane.The jump matrix of the RH problem of the initial boundary value problem can be explicitly expressed by the spectral matrix corresponding to the initial conditions and boundary conditions.

It is well known that the nonlinear Schrödinger equation can well describe the wave evolution in deep water and optical fibers [27，28].In addition，the nonlinear Schrödinger equation is also a general model for some multiplicity of nonlinear phenomena in plasma waves，Bose–Einstein condensates，and other physical phenomena [29–31].One of the most important applications is the soliton in optical fibers[32].Nonetheless，several phenomena can not be described by low order dispersion NLS equation.When considering the propagation of ultrashort pulses through the fiber，that is，pulses less than 100-fs，it has been shown that the model should include high-order dispersion，self-steepening，selffrequency，and high-order effects.The high-order nonlinear Schrödinger equation (1.1) is particularly important for describing the more complex phenomena.In this paper，we study the high-order nonlinear Schrödinger equation

suppose q(x，t) is a smooth solution of equation (1.1) for(x，t) ∈ R × [0 ，∞)which is x-periodic of period L ＞0，i.e.q(x+L，t)=q(x，t).We consider the following initial datum involving a single exponential:

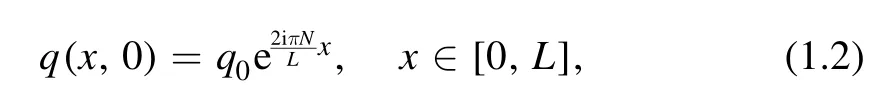
where N is an integer and the constant q0＞0.The high-order nonlinear Schrödinger equation has been studied through many methods，such as Darboux Transformation，the Inverse scattering transform and so on [33–41].However，to the best of our knowledge，the high-order nonlinear Schrödinger equation with periodic initial conditions was not reported before.Although we used the same method as in[25，26]，it is worth noting that the RH problem we studied was more complex.It lays the foundation for us to further explore a certain class of nonlinear integrable equations，such as the KdV equation，the mKdV equation，and the Hirota equation.

The outline of this paper is as follows: in section 2，we apply the UTM to a high-order nonlinear Schrödinger equation posed on a finite intervalx∈ [0 ，L] ⊂R.In section 3，the high-order nonlinear Schrödinger equation on the periodic problem with a single exponential initial data(i.e.q(x，0) =was considered.Moreover，by solving the associated RH problem involving the initial datum alone，the exact solution is obtained，which corresponds to the one-gap solution.

2.The UTM to the high-order nonlinear Schrödinger equation on a finite interval

In this section，we apply the UTM to the high-order nonlinear Schrödinger equation with the following data，

According to the AKNS formalism，the high-order nonlinear Schrödinger equation has a lax pair given by

with

where Ψ(x，t，λ) is a 2×2 matrix-valued function，λ∈C is an auxiliary(spectra)parameter，the potential matrix Q and σ3are defined by

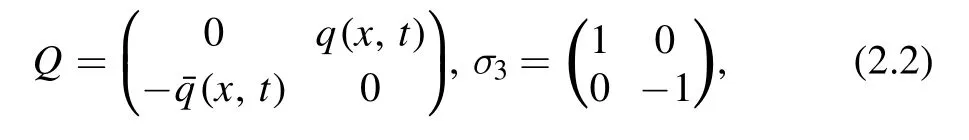
the W(x，t，λ) and θ are defined byW(x，t，λ)=(QΨ dx+VΨdt)，θ=λx+ (2λ2-8λ4)t.According to equation (2.1)，we get

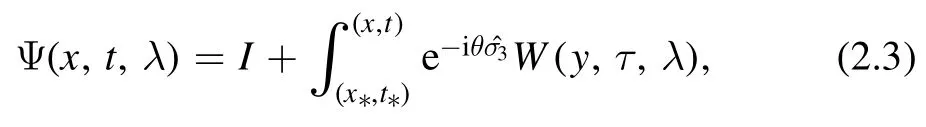
where (x*，t*)∈[0，L]×[0，T] is an arbitrary point and integral means the line integral that smoothly connects the indicated points.We choose the point (x*，t*) as each of the corners of the polygonal domain.Therefore we define four solutions Ψ1，Ψ2，Ψ3，Ψ4，corresponding to the four points (0，T)，(0，0)，(L，0)，(L，T).

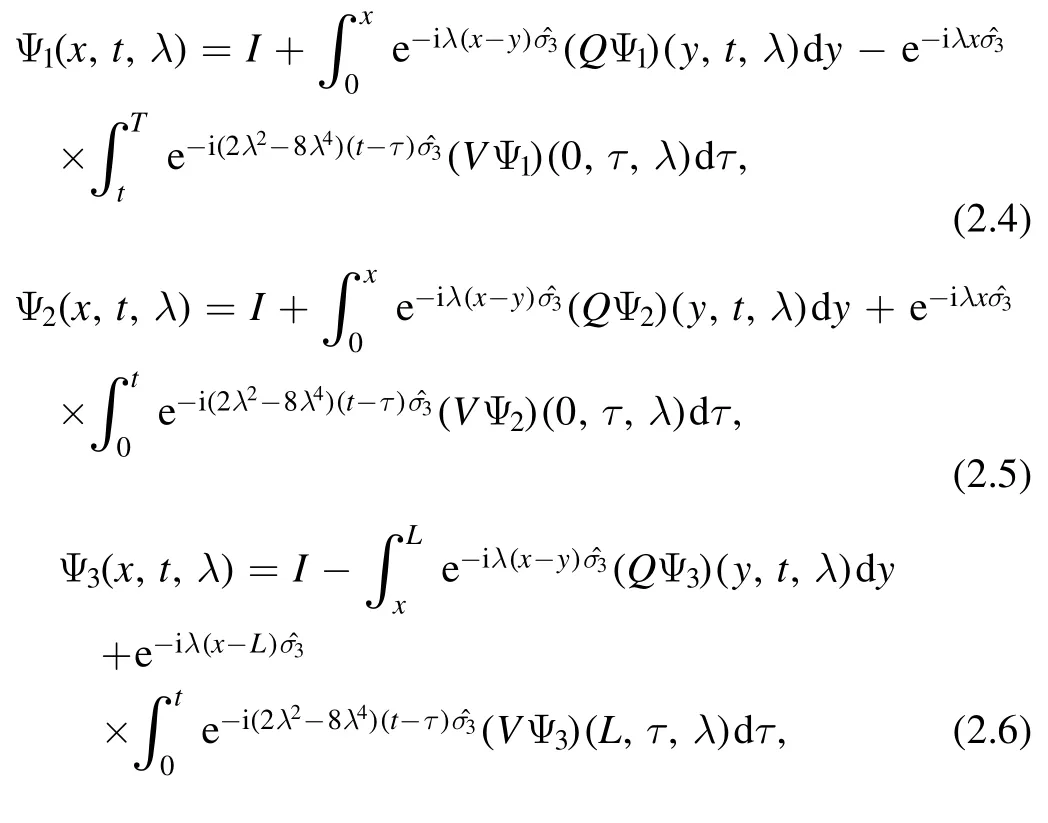
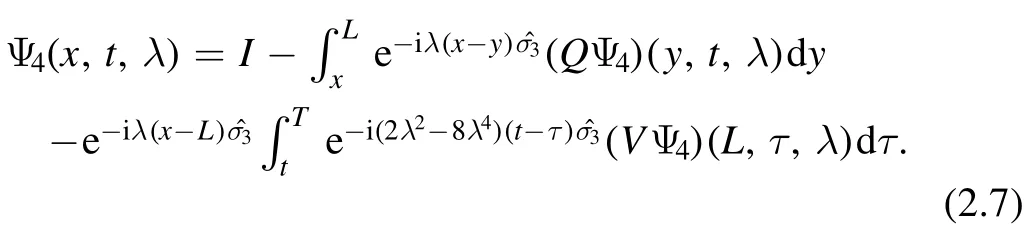
Further，we can show that Ψj(x，t，λ)，j=1，2，3，4 satisfies the following bounded and analytic properties in the complex λ plane

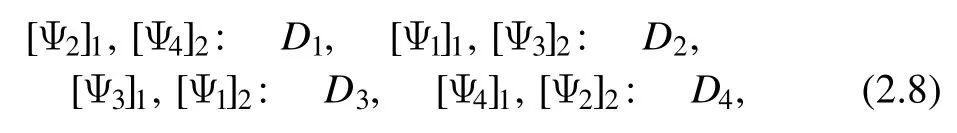
where [A]1and[A]2denote the first and second columns of a matrix A，respectively.The Dj(j=1，…，4) is defined as follows

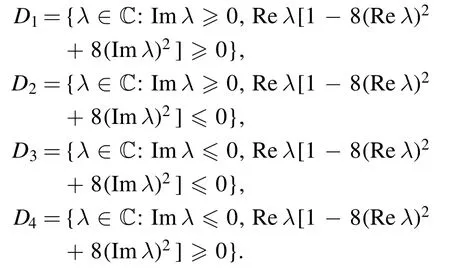
Note that all the Ψjare entire functions of λ，since the matrices Q and V are traceless，thus we have

The asymptotics here and later are in the corresponding domains of boundedness.See figure 1 for details.

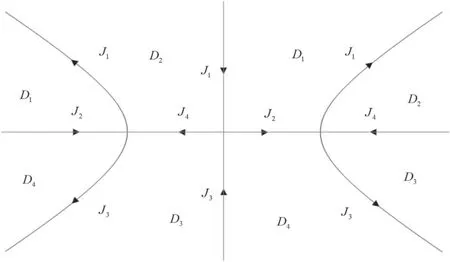
Figure 1.Since our analytical region here is different from[25，26]，we draw the integrable region and the direction of the integration curve for the RH problem according to the definition of Dj，as shown in figure 1.The jump matrices J1，…，J4 are defined in (2.25).

The eigenfunctions Ψjare related by the equations

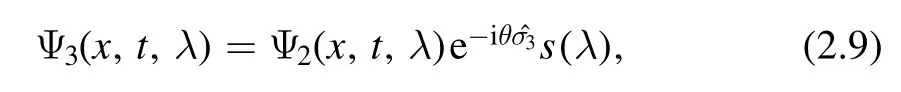
Through the above equation，we get

Meanwhile，equations (2.9) and (2.11) imply

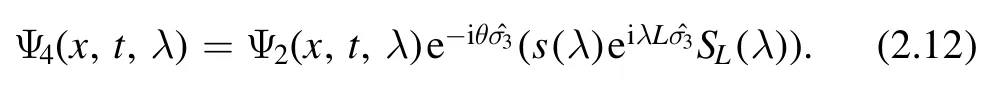
The (1，2)th element of above equation is

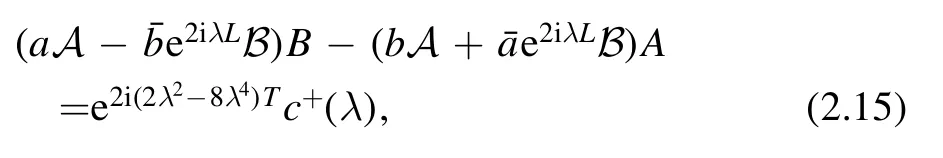
where

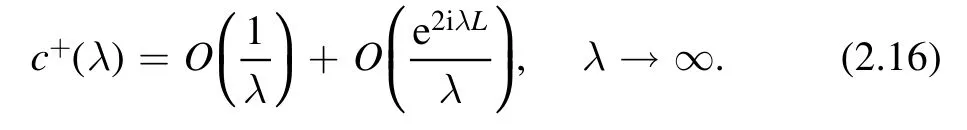
According to symmetry properties，we have

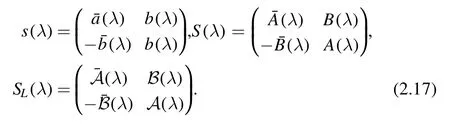
Here，and in what follows，a bar over a function denotes that the complex conjugate is taken，not only of the function but also of its argument;this is called the Schwarz conjugate.We can easily get the following properties:

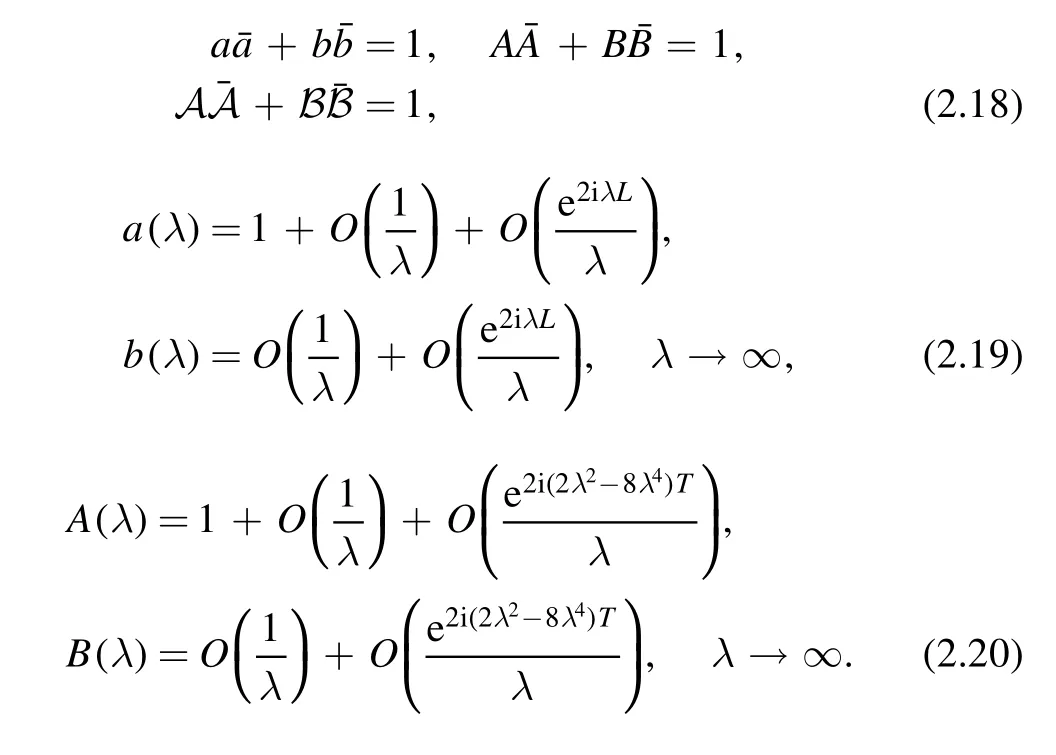
Now we construct the RH problem for M(x，t，λ)

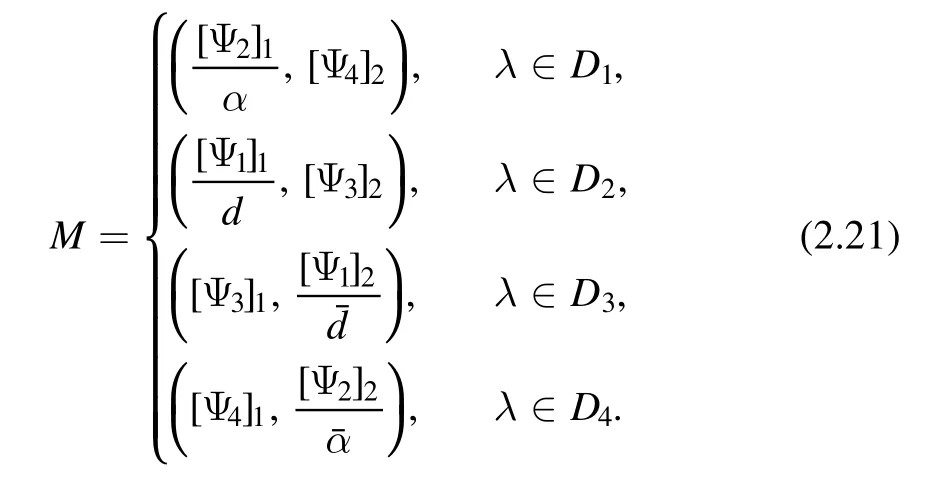
The M satisfies

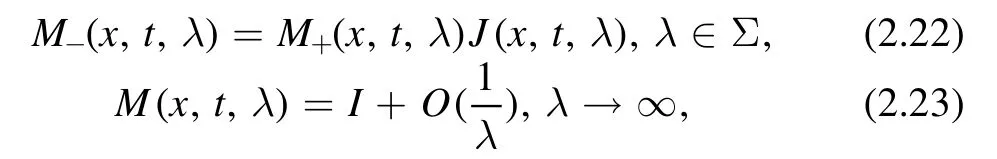
where

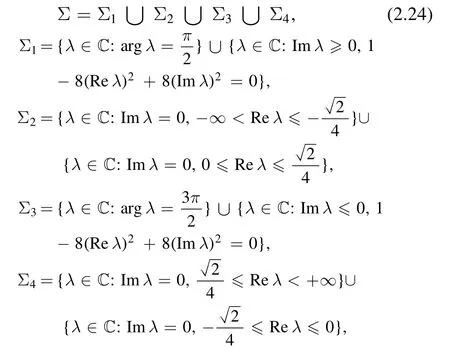
and the jump matrix J is defined by

where

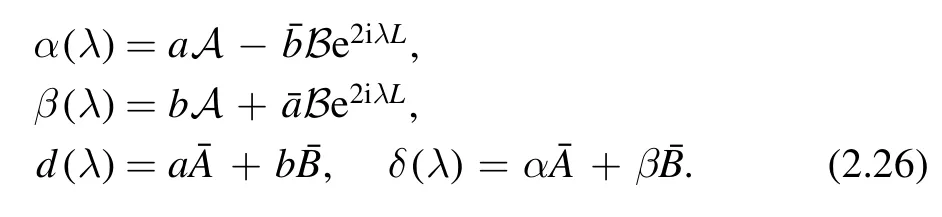
The solution q(x，t) of equation (1.1) can be recovered from

Note that jump matrix J depends on the initial datum q(x，0)and the boundary values q(0，t)，qx(0，t)，qxx(0，t)，qxxx(0，t)，q(L，t)，qx(L，t)，qxx(L，t)，qxxx(L，t).If all values are known，we can obtain the q(x，t) via the solution of the RH problem.

3.The high-order nonlinear Schrödinger equation on the periodic problem with a single exponential initial data

Suppose q(x，t) is a smooth solution of equation (1.1) for(x，t) ∈ R × [0 ，∞)which is x-periodic of period L ＞0，i.e.q(x+L，t)=q(x，t).We consider the following initial datum involving a single exponential:

where N is an integer and the constant q0＞0.In this case，we clearly have A=Aand B=B.Therefore the jump matrices Jidefined in equation (2.25) become

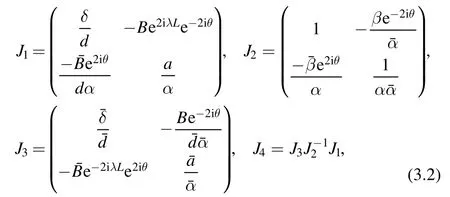
where

Similarly，we have

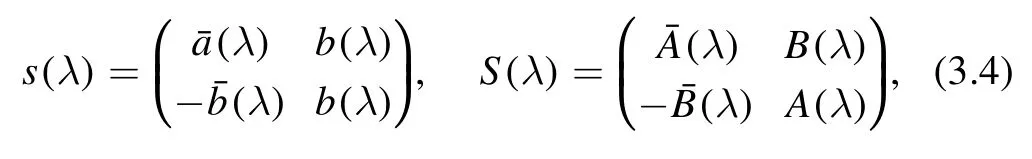
where

Clearly，S(λ)depends on T，while s(λ)does not.We have the global relation:

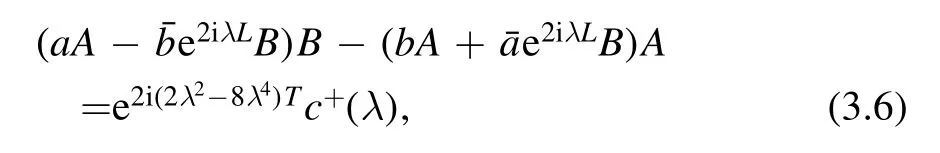
where

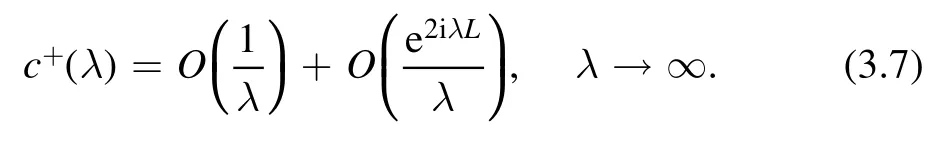
Meanwhile，a，b，A，B satisfy the equation (2.18)，equation (2.19) and equation (2.20).According to equation (2.27)，the solution q(x，t) of equation (1.1) can be recovered by

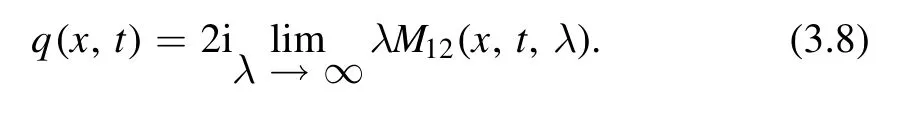
3.1.The RH problem for m

It can be formulated，which involves an RH problem where the ratio Γ=B/A is used to define the matrix jump，relative to A and B.Now we consider the piecewise meromorphic function m(x，t，k) defined by

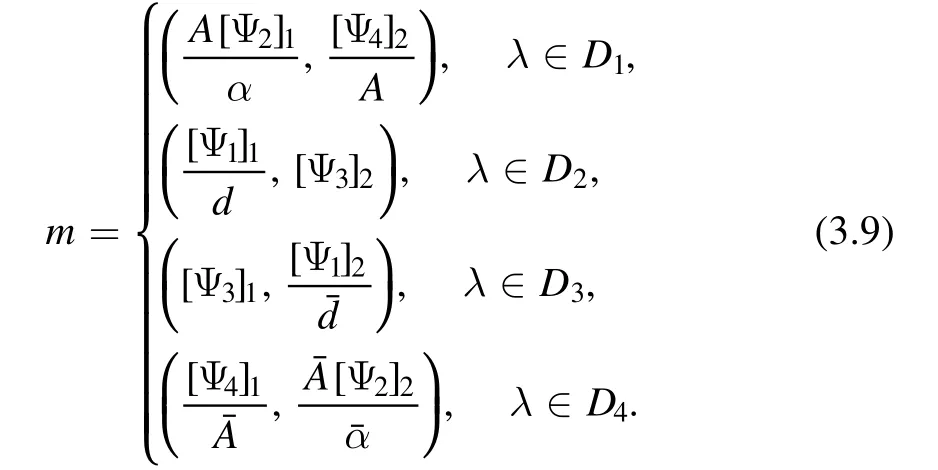
The relationship between functions m and M defined in equation (2.21) is as follows:

where the piecewise meromorphic function H is defined by

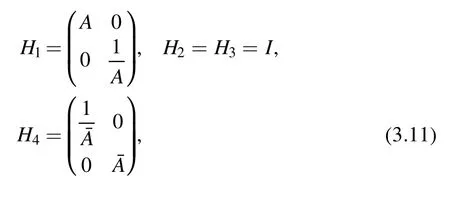
where Hjis defined in the region Dj，j=1，…，4.

We can get a RH problem for m as follows:

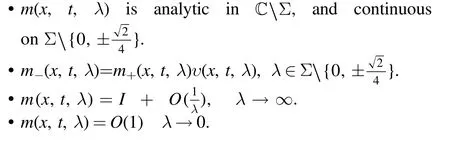
The jump matrix υ(x，t，λ) is defined by

Furthermore，the function m admit the symmetry relations

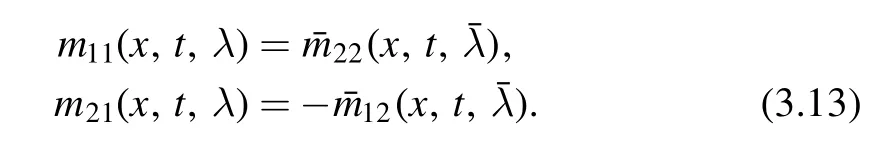
3.2.The RH problem for

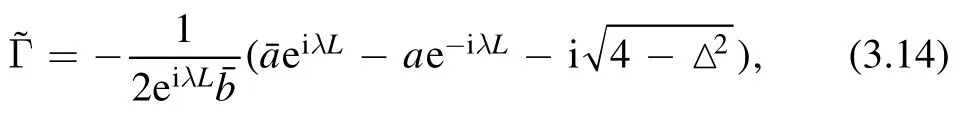
where △(λ) is given by

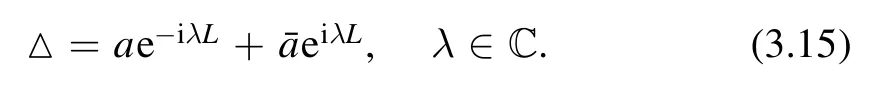
We define a(λ) and b(λ) in terms of the initial datum(3.1)，

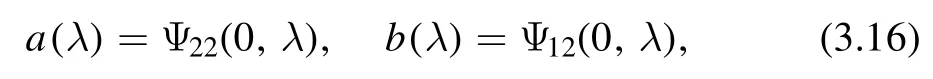
where Ψ12(x，λ) and Ψ22(x，λ) satisfy the following equation:

with Ψ22(L，λ)=1，Ψ22x(L，λ)=0.By direct integration of the above equation，we get the expressions of the spectral functions a(λ) and b(λ):

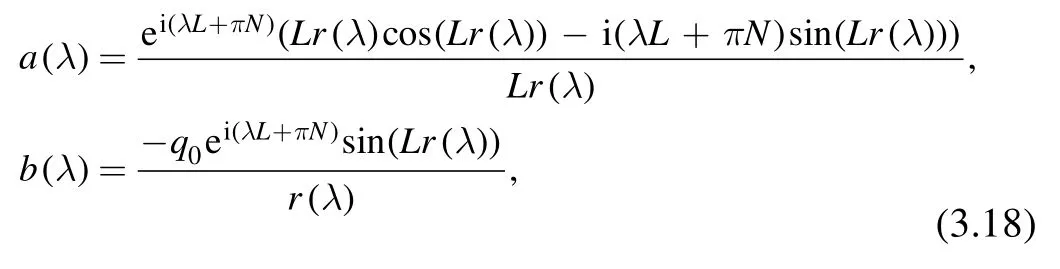
where

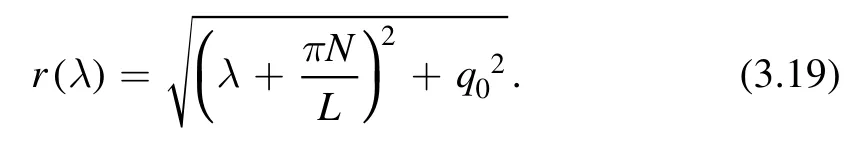
It follows that

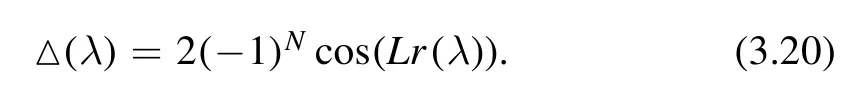
Even though r(λ) has a branch cut，we note that a(λ)，b(λ) and △are entire functions.The zeros of 4 -△2=4 ( sin (Lr(λ))consist of the two simple zeros λ±defined by

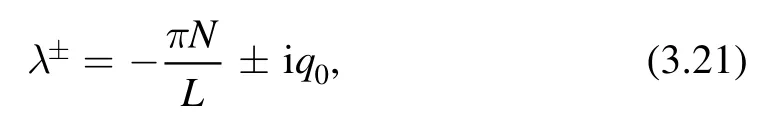
as well as the infinite double zeros

note that) has no poles.

In order to define a RH problem which depends oninstead of Γ，whereis independent of T，we defined the function g(λ) by

where gjis defined in the region Dj，for j=1，…，4.We defined(x，t，λ)by

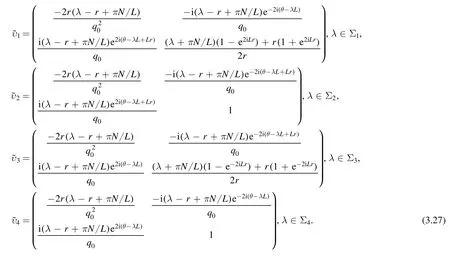
We draw the following figure according to all possible distributions of branch cutC，combined with the direction of the jump curve of the RH problem.See figure 2 for details.

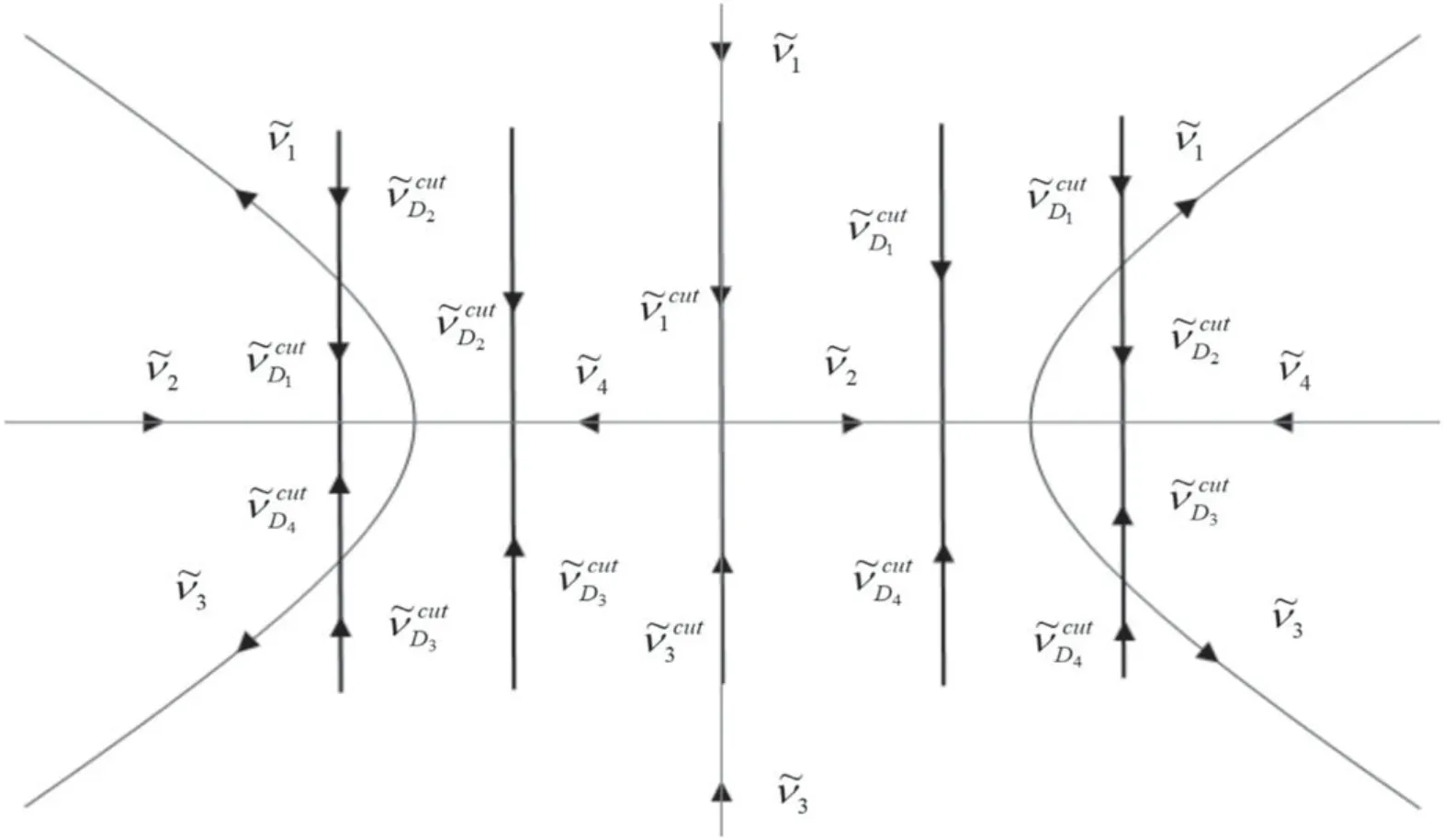
Figure 2.The contour n the complex λ-plane and the associated jump matrices for RH problem for

3.3.Solution of the RH problem for

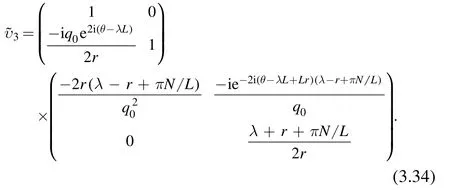
Then we define a new solutionby

where f(λ)≡f(x，t，λ) is defined by

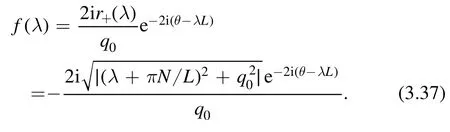
By performing another transformation，we find that the jump matrix equation(3.36)can be made constant(i.e.independent of λ).Define δ(λ)≡δ(x，t，λ) by

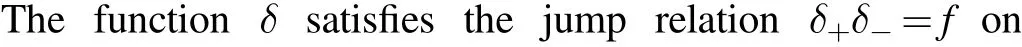
The unique solution of this problem is given explicitly by

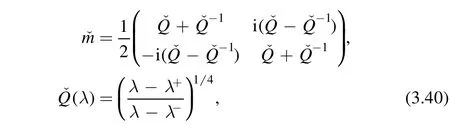
In order to calculate δ∞，we note that

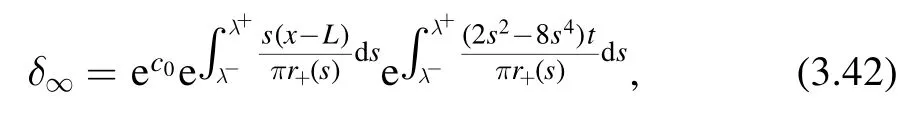
where c0is a constant

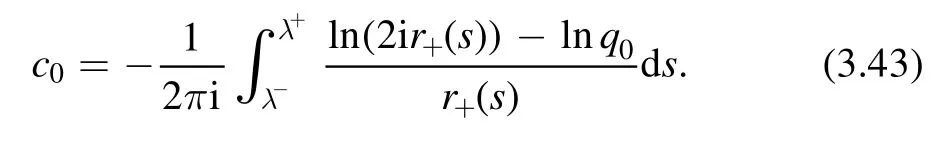
The integrals in equation (3.42) involving x-L and t can be obtained by opening the contour and deforming the contour to infinity:

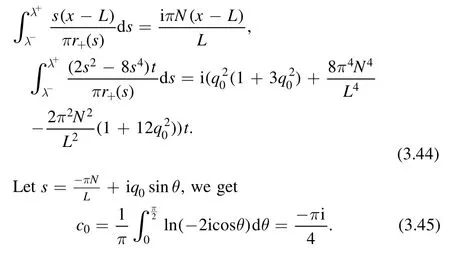
We finally get the expression of δ∞as follows

Substituting the above expression of δ∞into the equation(3.41)，we find that the solution q(x，t) of equation (1.1) corresponding to the initial datumis given by

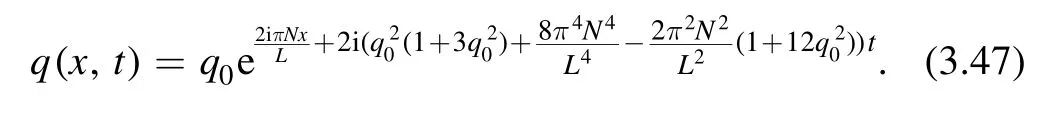
Meanwhile，it is easy to verify that this q(x，t)indeed satisfies the correct initial value problem.In the terminology of the finite-gap approach，this corresponds to one-gap solutions.

It is worth pointing out that equation(3.48)is consistent with equation (3.47) when N=0.

Acknowledgments

This paper is funded by National Natural Science Foundation of China(No.11471215).

Conflict of interest

The authors declare that they have no conflict of interest.