Effect of arbitrary matter-geometry coupling on thermodynamics in f(R) theories of gravity

Jun Wang，Ling-Xuan Qiang，Tian-Qiang Zhang，Zhi-Song Wang and Lu-Yu Li

School of Physics and Astronomy，Yunnan University，Kunming 650091，China

Abstract In this paper，the thermodynamics of the Friedmann–Lemaître–Robertson–Walker universe have been explored in f(R)theories of gravity with arbitrary matter-geometry coupling.The equivalence between the modified Friedmann equations with any spatial curvature and the first law of thermodynamics is confirmed，where the assumption of the entropy plays a crucial role.Then laws of thermodynamics in our considering case are obtained.They can reduce to the ones given in Einstein’s general theory of relativity under certain conditions.Moreover，a particular model is investigated through the obtained generalized second law of thermodynamics with observational results of cosmographic parameters.

Keywords: thermodynamics，f(R) theories of gravity，matter-geometry coupling

1.lntroduction

According to astronomical observational data，such as the type Ia supernovae (SNe Ia) [1，2]，the cosmic microwave background radiation [3–5] and the baryon acoustic oscillations[6–8]，it is known that our universe is currently in a stage of accelerating expansion.In order to provide a reasonable explanation for this observation，f(R)theories of gravity[9–11]have been taken into consideration，which are spirited candidates in modified theories of gravity.To replace the Ricci scalar R in the Einstein–Hilbert action by an arbitrary function of the Ricci scalar R，the gravitational action of f(R) theories of gravity can be obtained.This indicates that the relationship between these two theories of gravity is straight.Up till now，many aspects of f(R) theories of gravity，such as energy conditions [12–15]，cosmological perturbations [16–20]，cosmological dynamics[21] and instabilities [14，22，23]，have been studied.

With the strongest gravitational effect，black holes can be studied by quantum field theory in a curved background，usually known as the semiclassical quantum description of black holes，where matter can be dealt with with quantum field theory，while the gravitational field as a classical one is described by Einstein’s general theory of relativity (GR).As to the thermodynamics of black holes，temperature and entropy are two basic quantities.For the former one，it is proportional to the surface gravity of black hole horizons，usually known as the Hawking temperature[24]，while for the latter one，it is proportional to the area of black hole horizons，usually known as the Bekenstein–Hawking relation [25–27].Moreover，the temperature，mass and entropy of black holes conform to the first law of thermodynamics[25].

Since the temperature and entropy of black holes are determined by the space-time geometry，while the space-time geometry is decided by the Einstein field equations，there should be a relationship between the thermodynamics of black holes and the Einstein field equations.Then it has been found by Jacobson for the first time [28].The second law of thermodynamics (SLT) of black holes has been extensively studied in the framework of GR [29–35].

Taking the Friedmann–Lemaître–Robertson–Walker(FLRW) universe as a thermodynamical system，the method to study the thermodynamics of black holes can be applied to study the thermodynamics of cosmology.Cosmology usually takes the apparent horizon，the cosmic event horizon and the Hubble horizon into consideration.In a spatially flat universe，they have the same value.According to recent research，the cosmic event horizon does not always exist in cosmological models，while whether the Hubble horizon can be always related to thermodynamics is not sure[36].However，the first law of thermodynamics holds on the apparent horizon is not only right in GR [36] but also correct in f(R) theories of gravity[37，38].Therefore，the apparent horizon will be taken as the boundary of the FLRW universe in this work.

Recently，a more general type of f(R)theory of gravity has been proposed in reference [39]，where the matter-geometry coupling is arbitrary and the Lagrangian density of matter only appears in the coupling term [39].Due to the arbitrary mattergeometry coupling，the continuity equation of matter does not hold generally.Issues on energy conditions and stability have been investigated in this context [14].In this work，it is interesting to study the effect of the arbitrary matter-geometry coupling on thermodynamics in f(R) theories of gravity.

This work is organized as follows.The background of the present work is briefly reviewed in the following section.In section 3，the equivalence between the modified Friedmann equations with any spatial curvature and the first law of thermodynamics is proved in our considering situation by two different approaches.In section 4，the generalized SLT is explored in our considering case and then used to study a particular model，where observational results of cosmographic parameters are taken into consideration.The last section is devoted to conclusions.

2.f(R) gravity with arbitrary matter-geometry coupling

In this work，the considering action is [39]

where fi(R) (i=1，2) and G(Lm) are arbitrary functions of the Ricci scalar R and the Lagrangian density of matter Lmrespectively.Throughout this work，we set the units to 8πG=c=1.It is obvious that Lmonly appears in the coupling term and the matter-geometry coupling is arbitrary[39].When f2(R)=1 and G(Lm)=Lm，action(1)reduces to the case in f(R)theories of gravity without coupling.Moreover，when f1(R)=R，the situation in GR is obtained.If f2(R) is redefined as 1+λf2(R)and G(Lm)is taken as Lm，the framework of f(R)theories of gravity with non-minimal coupling can be achieved.It is clear that f(R) theories of gravity with arbitrary mattergeometry coupling are more general，in which all the above mentioned instances are included as special cases.

Varying action (1) with respect to the metric gμν，the field equations are

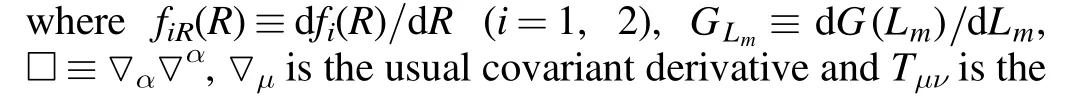
Taking the covariant divergence of the field equations (2)，we have

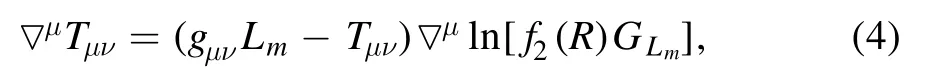
where the Bianchi identities and [□，"ν]fiR=Rμν"μfiR[40]have been used.It is clear that Tμνis not conserved due to the arbitrary matter-geometry coupling.

On cosmic scales，due to the constraint from the cosmological principle，the geometrical structure of the spacetime can be described by the FLRW metric as

where t，a(t) and k are the cosmic time，the scale factor and the spatial curvature constant，respectively，and dΩ2≡ dθ2+sin2θdφ2，and Tμνcan be taken as

where ρ，p and Uμare the energy density，the pressure and the four-velocity of the perfect fluid，respectively.Considering above mentioned facts，the Friedmann equations of f(R) theories of gravity with arbitrary matter-geometry coupling can be given as

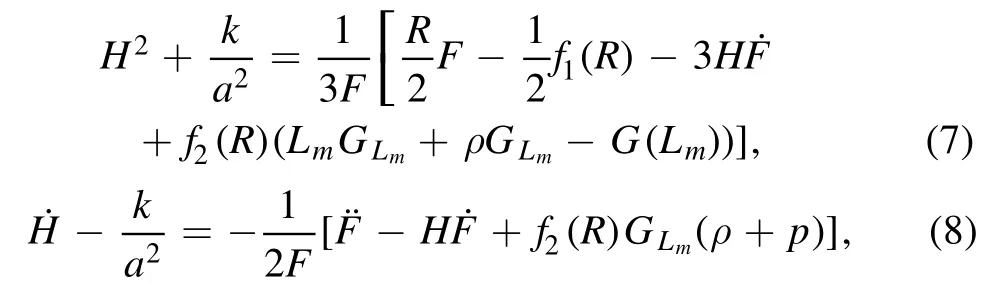
whereH≡F ≡f1R(R)+2G(Lm)f2R(R) and the over dot implies derivative with respect to t.

In the FLRW universe，by noticing the Einstein convention for summation，equation (4) yields

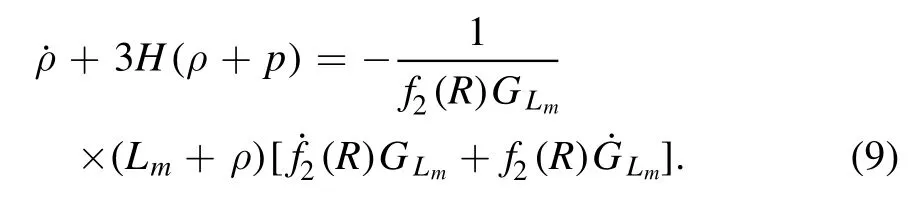
It is obvious that the law of conservation of matter can be held if one takes Lm=-ρ.Otherwise，the characteristics and the generality of this model will disappear.This condition will be taken into consideration in the following work.

3.1st law of thermodynamics

For the convenience to introduce the definition of the apparent horizon，the metric (5) is rewritten as

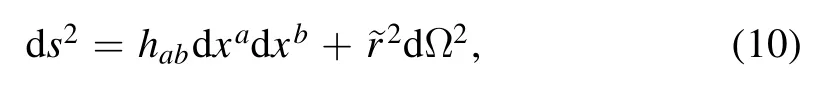
Then，in the FLRW space-time，the radius of the apparent horizonis

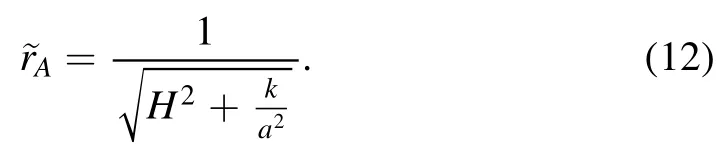
It is obvious that when k=0，is just the same as the radius of the Hubble horizon.

It is known that the temperature of black holes is described by the Hawking temperature，which is proportional to the surface gravity of black hole horizons [24].Taking the FLRW universe as a thermodynamical system with the apparent horizon，similar to the definition of the Hawking temperature，we assume that the temperature of the FLRW universe can be defined as

where κ is the surface gravity of the apparent horizon，which is

Note that the absolute value sign has been introduced to avoid a negative temperature.

Combining the differential form of definition (12) with equation (8)，we have

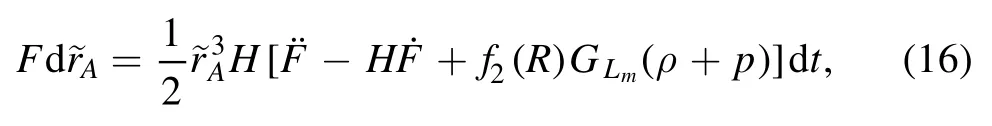
In our considering case，the total energy of matter can be expressed as

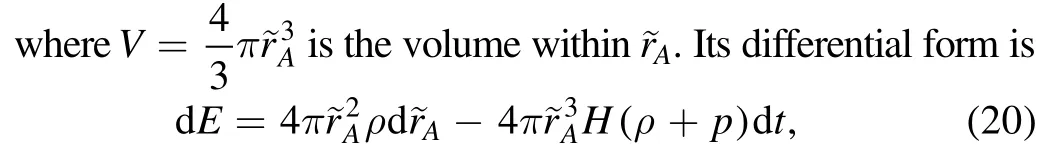
where conditions to keep the conservation law of matter and the continuity equation are used in calculations.Substituting the relationship (20) into equation (18)，we find that

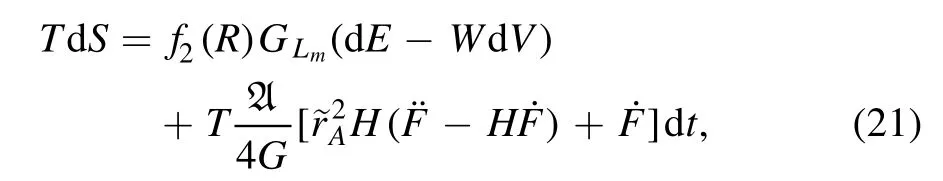
For convenience，we introduce three symbolizations that are

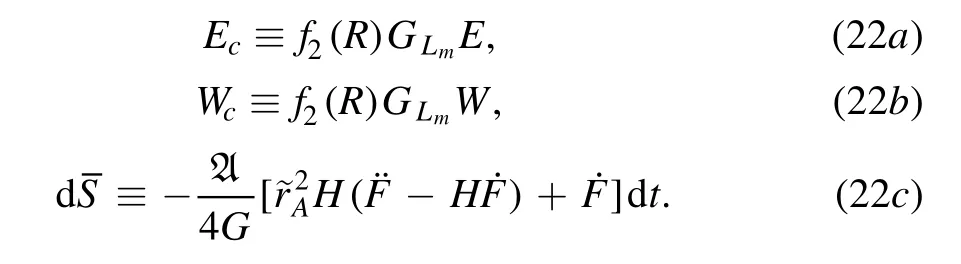
Using these symbolizations，equation (21) can be rewritten as

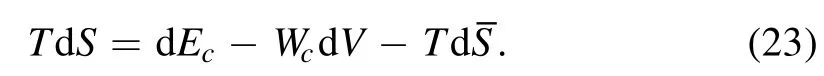
If we take d≡ d (S+)as the effective entropy of the FLRW universe with the apparent horizon during dt，equation(23)reads

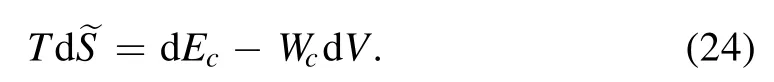
When the arbitrary matter-geometry coupling disappears，i.e.f2(R)=1 and G(Lm)=Lm，equation (21) reduces to the case in f(R)theories of gravity without coupling，which is consistent with the one given in[37].Furthermore，when f1(R)=R，the situation in GR can be achieved.Moreover，if f2(R) is redefined as 1+λf2(R) and G(Lm) is taken as Lm，the first law of thermodynamics in f(R) theories of gravity with non-minimal coupling can be found，which is the same as the one given in [38].

Alternative to the above mentioned approach，the first law of thermodynamics in our considering situation can also be obtained in the following way.In GR，the definition of the entropy of the FLRW universe with the apparent horizon is given bySE≡A4G.Then the thermodynamical fluid δQ is

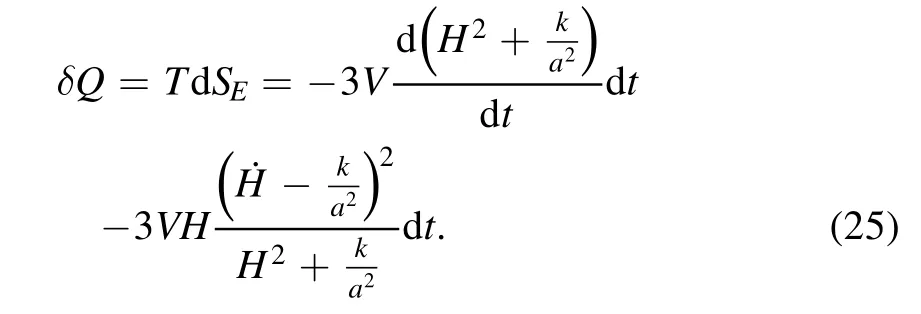
It is obvious that δQ is formulated by purely geometrical terms In order to make physical sense of it，the Friedmann equations should be taken into consideration.

Generally，the Friedmann equations of any generalized gravitational theory can be written in the form of GR，i.e.

where ρt≡ρ+ρfeand pt≡p+pfe，where ρfeand pfesignify the energy density and pressure of modified terms，respectively.The right side of equation (26) can be written as a function，i.e.

Taking the time derivative of equation (28)，the formula (25)reads

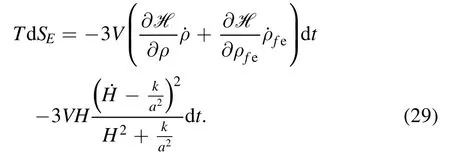
Considering the factor(3 ∂ H ∂ρ)-1in the last equation，we have

Using the law of conservation of energy，we get

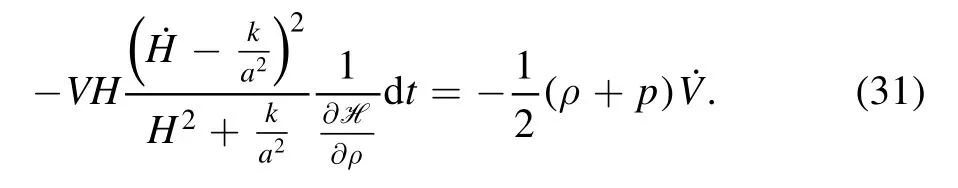
Then equation (30) can be written as

If the entropy of the FLRW universe can be defined as

we have

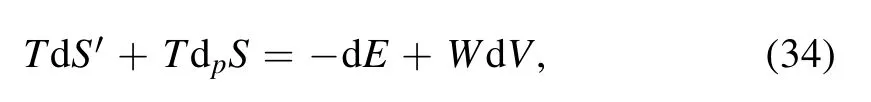
where dpS is defined as

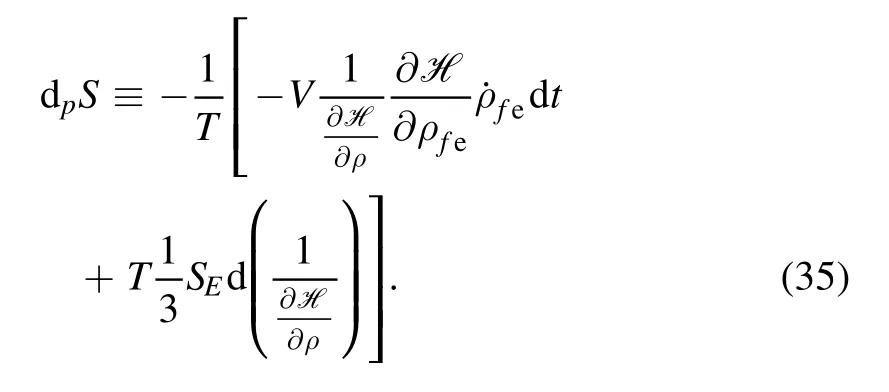
Equation (34) is the first law of thermodynamics for the FLRW universe with the apparent horizon in generalized theories of gravity，whereS′ denotes the entropy-area relation and dpS stems from modified terms.Since modified terms change over time normally，dpS can be interpreted as the entropy production of the non-equilibrium according to[51，52].Formulas ofS′ and dpS are determined by the theory of gravity under consideration.In our considering case，S′ and dpS are just entropies(15)and(22c)，respectively，and then equation (34) is just equation (23).

4.Generalized 2nd law of thermodynamics

In the following，SLT for the FLRW universe with the apparent horizon will be studied in f(R) theories of gravity with arbitrary matter-geometry coupling.Due to the arbitrary matter-geometry coupling and modified terms，SLT is usually called the generalized second law of thermodynamics(GSLT)in generalized theories of gravity.

The ordinary SLT states that for irreversible processes in isolated systems，the entropy of the system always grows.From equation (24)，entropies that should be taken into consideration are S，Sand Sm，where Smdenotes entropies of matters and energy fields in the FLRW universe and can be given by the Gibb’s equation as [53]

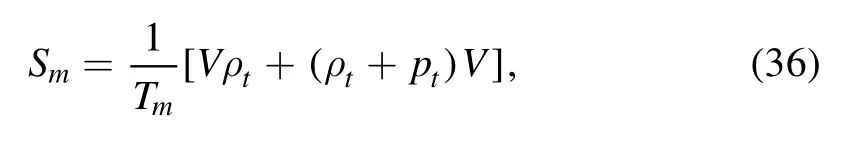
where Tmrefers to the temperature of the total energy in the FLRW universe.Since there may be energy flows，Tmis not normally equal to the boundary temperature T.Therefore，one can introduce the temperature parameter b to make Tm=bT[54，55].In order to confirm that Tmis not negative and no larger than T，b should satisfy 0 ＜b ≤1，where b=1 indicates the boundary of the FLRW universe is in thermal equilibrium with its inside.

According to the ordinary SLT，GSLT in our considering case can be expressed as

Considering equations (24) and (36)，we have

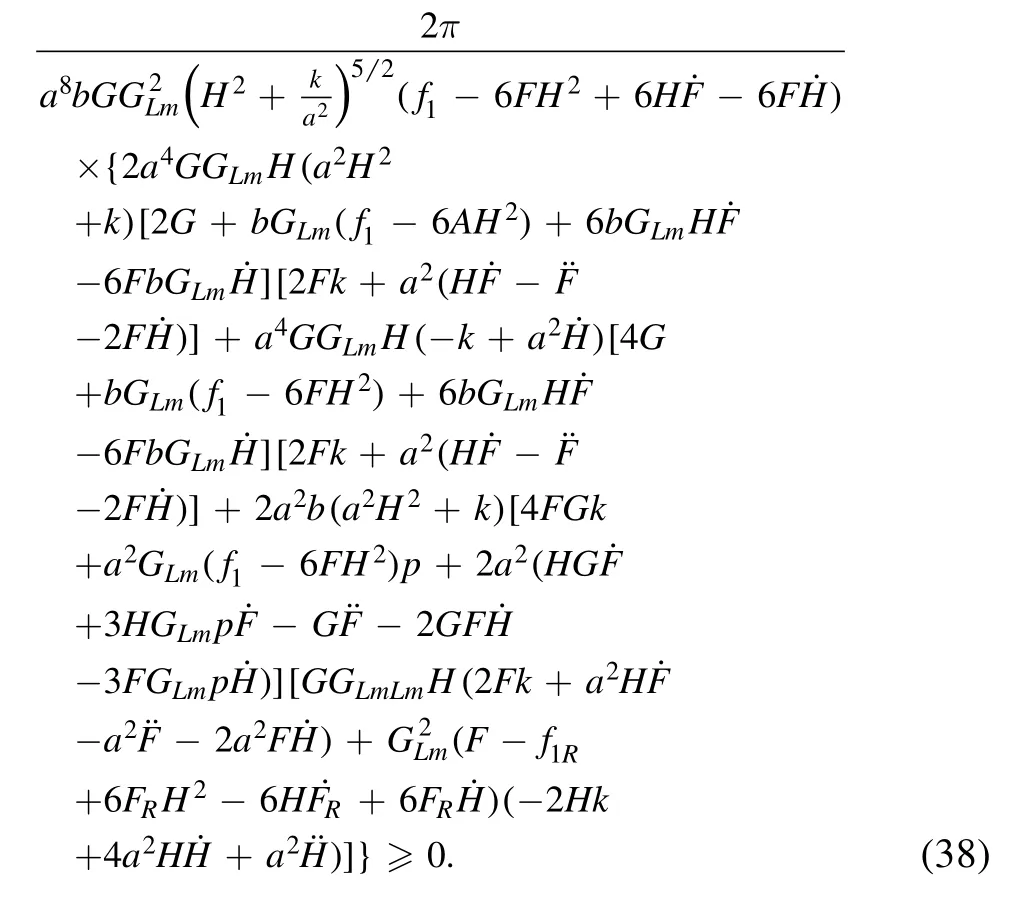
This is GSLT for the FLRW universe with the apparent horizon in f(R) theories of gravity with arbitrary mattergeometry coupling.To obtain this result，the Friedmann equations (7) and (8)，and the continuity equation are used.

When f2(R)=1 and G(Lm)=Lm，GSLT in f(R) theories of gravity without coupling can be obtained，which is consistent with the one given in [37].Furthermore，when f1(R)=R，the situation in GR can be attained，which is

In what follows，we apply the obtained GSLT to study a particular model in the flat universe (k=0)，where f1(R)=R，f2(R)=αRnand G(Lm)=Lm，where α and n are constants[56].It is known that R and its time derivatives can be represented by observational parameters of the deceleration(q)，the jerk (j) and the snap (s) [57–60]，i.e.

where

Since the snap(s)still has no reliable observational result，the terms containingwill be omitted.In our considering case，GSLT (38) reads

According to observational data，present values of corresponding parameters are taken as H0=67.4±0.5 km s-1Mpc-1[61]，q0=-0.81±0.14 andj0=[62].Moreover，to avoid instability，we take n=2 [63] in the following discussions.For comparison，the case where n = -2 is also studied.Corresponding results are shown in figure 1.

Figure 1.Ranges of the parameter α are constrained by the obtained GSLT for the model with f1(R)=R，f2(R)=αRn and G(Lm)=Lm.(a) n=2.(b) n=-2.

It is clear that for n=2，α ＜0.When the value of the temperature parameter b is proceeding to zero，the range of the parameter α is getting wide.While，when b →1，the range of the parameter α is becoming narrow，but its value increases.When b=1，the parameter α has the narrowest range.However，the situation is reversed for n = -2.

5.Conclusions

In this work，the thermodynamics of the FLRW universe with the apparent horizon has been studied in f(R) theories of gravity with arbitrary matter-geometry coupling.Taking the FLRW universe as a thermodynamical system，we assume that the way of the Hawking temperature and the Bekenstein–Hawking relation are defined on black hole horizons can be generalized to the apparent horizon of the FLRW universe.Based on this，we first confirm that the equivalence between the spatial component of the modified Friedmann equations with any spatial curvature and the first law of thermodynamics exists in our considering case.Then the first law of thermodynamics is obtained，but additional terms appear.Some additional terms arise from arbitrary matter-geometry coupling，while others come from modified terms and can be explained as the entropy production of the non-equilibrium.For this confirmed equivalence，the definition of the entropy plays a crucial role，which means that whether the proved equivalence can be obtained is determined by the generalized entropy-area relation.

Alternative to the above mentioned approach，we also confirm the equivalence between the temporal component of the modified Friedmann equations with any spatial curvature and the first law of thermodynamics by the Clausius relation，where additional terms also appear.Since it is studied from the functional point of view，the obtained first law of thermodynamics is general and determined by the gravitational theory under consideration.In our considering case，it becomes equation (23).

It is clear that both components of the modified Friedmann equations with any spatial curvature are equivalent to the first law of thermodynamics in f(R) theories of gravity with arbitrary matter-geometry coupling.The confirmed equivalence indicates that a general entropy-area relation should be taken into consideration.Moreover，under particular conditions，the obtained first law of thermodynamics can reduce to the situation in f(R)theories of gravity with non-minimal coupling，f(R)theories of gravity without coupling and GR，respectively.

For SLT，it is usually called GSLT in modified theories of gravity.To obtain GSLT in our considering case，the entropy-area relation，the entropy production of the non-equilibrium and entropies of matters and energy fields should be taken into consideration.Then GSLT is obtained.It is worth mentioning that under certain conditions，the obtained GSLT can reduce to the case given in f(R)theories of gravity with non-minimal coupling，f(R) theories of gravity without coupling and GR，respectively.

Moreover，we apply the obtained GSLT to study a particular model，where observational results of cosmographic parameters are used.The result shows that when the boundary and the interior of the FLRW universe gradually approach the thermal equilibrium，the range of the model parameter α is becoming narrow.When they are in thermal equilibrium，α has the narrowest range.

Acknowledgments

This work is supported by the National Natural Science Foundation of China under Grant No.12165021 and Science Technology Department of Yunnan Province—Yunnan University Joint Funding (2019FY003005).