基于GPR的连续梁桥可靠度及最优维护策略研究

王向阳 黎恩华

(武汉理工大学交通与物流工程学院1) 武汉 430063) (中国轻工业长沙工程有限公司2) 长沙 410114)

0 引 言

高斯过程(Gaussian progress, GP)在可靠度领域应用中作为一种具有监督性质的机器学习方法，与人工神经网络等方法相比，在理论基础上更为严格，同时在多变量、小样本的非线性复杂工程问题中具有良好参数自适应性和学习能力.目前，国内外基于高斯过程回归模型的桥梁可靠度研究仅处于理论阶段.苏国韶等[1]将高斯过程模型用以重构边坡的极限状态函数，并结合可靠度理论计算相应的失效概率.赵伟[2]将蒙特卡罗法分别应用于高斯回归模型和高斯分类模型来求解大型复杂结构的可靠指标，研究证明与传统方法相比，这两种方法均有较高的精度和计算效率.

在可靠度研究的基础上，对桥梁维护决策进行优化处理也是一项重要的课题.Miyamoto等[3]以桥梁的耐久性和承载力为关注重点，引入遗传算法得到寿命期内最佳的维护计划.杨伟军等[4]围绕维修成本和失效损失构造优化决策函数，从动态可靠性角度对桥梁维护方案进行了探讨.但是有关多跨非对称PC连续梁桥这种具有多种失效模式复杂结构的体系可靠度和相应最优维护策略方向的研究较少.

文中考虑采用高斯过程回归模型作为桥梁结构功能函数的替代模型，并引入可靠指标矢量法和PNET法求解各失效模式之间的相关性问题，同时在考虑材料时变效应的基础上，运用遗传算法得到桥梁全寿命周期内最优维护方案.

1 高斯过程回归模型

高斯过程是基于随机变量的一种集合，同时高斯过程可以作为实际随机过程的近似处理.在函数空间内，高斯过程的分布可以看做是由均值函数m(x)和协方差函数k(x,x′)组合而成.

m(x)=E[f(x)]

(1)

k(x,x′)=E[(f(x)-m(x))(f(x′)-m(x′))]

(2)

因此高斯过程可以简写为

f(x)～GP(m(x),m(x),k(x,x′))

(3)

为了方便起见，在分析过程中将高斯过程的均值函数设为零，这样整个高斯过程只需要找到合适的协方差函数就可以按式(1)～(2)来表示.由于平方指数协方差函数(简写SE)在大多数问题中都表现出良好的适应性，所以其经常被选做高斯过程回归(Gaussion process regression,GPR)模型中的协方差函数.其一维函数形式为

(4)

式中：xp,xq为原始数据集中的某个输入向量；l,σf,σn均为GPR模型中的超参数.

对于文中求解桥梁可靠度的部分，提取训练样本数据的方法属于计算机模拟试验，假设观察结果是无噪声的才是合理的.所以忽略噪声影响，即SE协方差函数中的σn=0 .基于高斯分布的先验理论可得到样本数据中训练样本和测试样本输出的联合分布为

(5)

式中：K(X*,X)为对所有样本集中训练点和测试点进行估算的m×n阶协方差矩阵，其余元素K(X,X),K(X*,X*)也是类似的含义.进一步可推得高斯过程回归预测的决策函数为

(6)

2 基于GPR的体系可靠度计算方法

2.1 结构可靠度计算方法

(7)

运用JC法或设计验算点法在失效面上选取点x*对式(7)进行Taylor展开同时只取其中一阶偏导项，则可得：

(8)

(9)

设计验算点坐标可表示为

(10)

定义变量xi的灵敏度系数为

(11)

根据正态分布的相关变换性质可以得到：

(12)

(13)

则可推得最终可靠指标表达式为

(14)

2.2 失效模式之间的相关性分析

引入可靠指标矢量法将各失效模式间的关系以矩阵的形式表述，变成通过一个多维正态分布问题的求解.相关理论推导如下.

结构的基本随机变量为X=(X1,X2,…,Xm)T，第i个失效模式的第j个失效状态对应的功能函数表达式为

(15)

将随机变量X转换成独立标准正态随机变量Y，则相应的功能函数为

(16)

在验算点在验算点y*处将式(16)泰勒展开并保留一阶项，得到Zi的近似表达ZLi并根据式(11)和式(14)可得：

(17)

(18)

(19)

(20)

在得到结构不同失效模式间的相关系数矩阵后，可以选用概率网络估算技术(probabilistic network estimation technique，PNET)对相关系数矩阵进行分析从而求解体系可靠度.

3 维修策略计算原理

Kong等[5]提出采用叠加的原理计算维护策略下的可靠指标，叠加公式为

(21)

式中：β(t)为处于维护状态结构时刻t的可靠指标；β0(t)为不采取维护行为时结构可靠指标； Δβi(t)为第i个维护措施对结构可靠指标的提升量；n为结构在服役期内的维修次数，维护活动下可靠指标变化见图1.

图1 可靠指标变化图

图1中实线和虚线分别对应有无维护活动下的可靠指标波动情况，通常一种维护行为有三个关键时间节点：①图中维护行为开始的ts时刻，结构性能在得到改善且相应的可靠指标提升至rs.②维护效果的结束时刻ti，维护行为使得结构能够在一段时间内保持当前的性能状态，随后可靠指标将线性增长至re.③维护行为终止时刻te，此刻维护效应不再对未来结构的性能产生影响，结构性能将继续依照原有的衰变规律进行.Δβ需要随着维护活动的不同而进行相应的调整.

当结构退化模型考虑维护措施时，其在服役期内产生的维护成本波动见图2.假定对结构未进行维护活动之前估算的可靠指标为β0，衰变速率为a1，在t1时刻结构首次进入某种维护状态，相应的可靠指标提升r1及产生Ca,1的维护成本.随后，结构性能仍处于退化状态，衰变速率为a2.在t2时刻结构第二次进入某种维护状态，与首次类似，其可靠指标提升r2及产生Ca,2的维护成本，再继续以a3的速率退化.则可得出结构在有维修行为的服役时间t的累计维修成本AC(t)为

(22)

式中：n为结构总的维修次数；Ci(t)为一次维护活动的寿命周期成本.

图2 结构在维护活动下的维护成本

4 方法验证

图3的索梁体系[6]中，一等截面梁长2l=9.753 6 m.梁所承受的均布荷载q、极限抗弯强度M，以及钢索的屈服强度fy均服从正态分布且完全独立，索1和索2截面面积分别为6.45×10-2mm2和3.32×10-2mm2.统计参数见表1.

图3 索梁结构

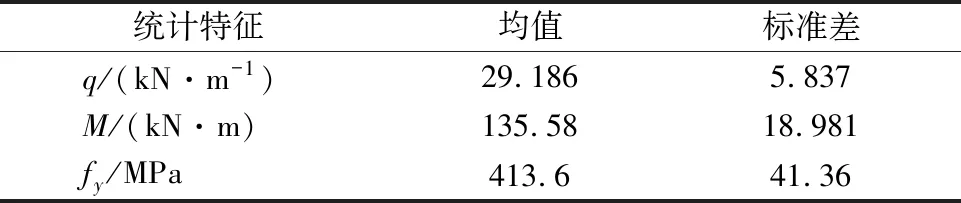
表1 随机变量统计参数表

以下为该结构可能出现的失效模式(见图4)和对应的功能函数.

图4 索梁结构失效模式

(23)

g2(X)=F1l+2F2l-2ql2

(24)

(25)

g4(X)=2M+F1l+2F2l-ql2

(26)

式中：F1为钢索1的极限抗拉能力，F1=A1fy；F2为钢索2的极限抗拉能力，F2=A2fy.

采用拉丁超立方抽样抽取均布荷载、抗弯能力,以及屈服强度这三个随机变量组成的样本120组，其中100组为训练样本，20组为测试样本.通过高斯过程回归自适应超参数分别获取以上四个功能函数函数下的GPR模型，并计算相应的可靠指标见表2.

表2 索梁结构计算结果

四种失效模式间相关系数矩阵的计算结果为

应用PNET法，取临界相关系数ρ0为0.8，那么该系统的主失效模式为失效模式1和失效模式2，则该串联结构的体系可靠指标β=3.167 4，可靠概率R=0.999 2.为了校核体系可靠度的计算误差，采用Monte-Carlo数值模拟方法抽取106个样本计算该结构的可靠度概率RMCS=0.999 223.由此可知基于高斯过程回归的PNET法计算多失效模式下的体系可靠度是具有一定可行性的.

5 多跨连续梁桥工程应用实例

5.1 工程概况

湖北省荆州市海子湖特大桥为多跨非对称变截面连续梁桥，整体一联布置，桥跨布置为65 m+123 m+156 m+123 m+10×90 m+55 m，全长1 434 m.该桥主梁采用C55混凝土，上部结构采用预应力混凝土变截面连续箱梁，采用分两幅布置，单幅桥宽16.9 m，为单箱双室直腹板截面形式.该桥小里程方向0号桥台为肋板式轻型桥台，大里程方向为15号桥台为重力式U型桥台.该桥的桥型布置图见图5.

图5 海子湖特大桥布置(单位：m)

5.2 有限元模型

采用midas-Civil建立桥梁的上部结构有限元模型,见图6.

图6 上部结构有限元模型

对于研究目标的下部结构是指海子湖特大桥的桥墩和承台组成的结构体系，由于该桥桥墩较多，逐一建模分析研究十分困难，所以文中对于该桥下部结构体系可靠度分析的对象是最容易出现破坏可能性的某个桥墩.通过对上部结构在正常使用极限状态下的有限元模型分析，可得到各桥墩的支座反力值，从而找到所受反力值最大的那个桥墩，见图7.

图7 各基础结构反力示意图

可知该桥P3号桥墩的支座反力最大，所以本节将P3号桥墩作为研究对象.P3号桥墩为矩形空心墩，其承台尺寸为12.25 m×16.5 m×4.5 m，采用C35混凝土，桥墩横向宽11.5 m，顺桥向宽5m，采用C40混凝土.挡块和支座垫石分别采用C40混凝土和C55混凝土.

应用有限元软件ANSYS建立P3桥墩实体模型见图8，混凝土采用主要用于构造三维固体结构SOLID45单元.

图8 下部结构有限元模型

5.3 失效模式分析

在预应力混凝土连续梁桥服役阶段，桥梁的性能会受到许多因素的影响.在文献[7]的基础上，选用若干对桥梁结构体系可靠度分析影响程度较大的随机变量作为研究目标，各随机变量及相应统计参数见表3.

在文献[8]的基础上，失效形式主要考虑该桥在正常使用极限状态下可能由于应力或挠度超限引起结构失效，建立极限状态方程如下：

(27)

式中：δ、σcc、σct分别为桥梁关键截面的挠度、压应力和拉应力响应值，均可通过有限元软件计算得到.

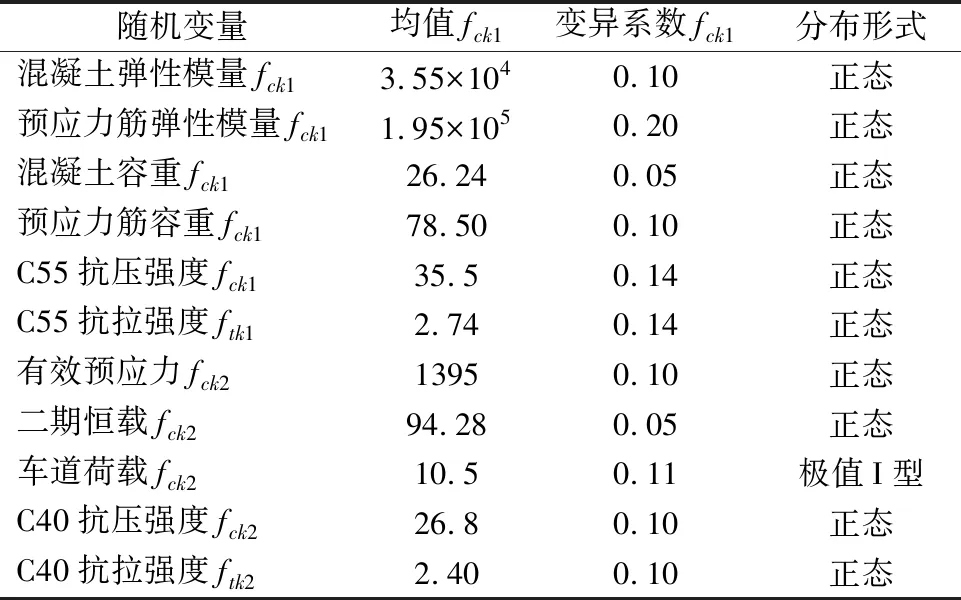
表3 随机变量的统计特征 单位：MPa

结合该PC连续梁桥有限元模型的计算结果、桥梁监控原则和相关荷载试验报告，将应力值较大或较小和挠度值较大的截面作为此桥可靠度分析中重点考虑的关键截面.限于篇幅，相关应力云图略.

由应力云图可知：海子湖特大桥上部结构各跨跨中截面和桥墩根部截面均是容易出现应力或挠度超限的关键截面.而对于下部结构来说，出现最大拉应力的部位为两挡块中间处，最大拉应力值为1.98 MPa,最大压应力出现在支座垫石附近，压应力最大值为12 MPa.P3号桥墩在支座垫石处选用的是高强度C55小石子混凝土，对于计算得到的压应力能够有效地承受，而挡块附近选用的C40混凝土，其极限抗拉强度与计算值十分接近且空心墩确实容易在服役一段时间后由于局部应力应作用产生顺桥向的裂缝，因此下部结构主要考虑挡块附近的拉应力失效模式.

运用拉丁超立方抽样方法(Latin hypercube sampling,LHS)抽取表3中70组样本数据，其中50组为训练样本，20组为测试样本.由于上部结构和下部结构的混凝土强度标准值抽样数据是用作后续运算求解功能函数值，所以不直接代入有限元模型计算，而其余变量需要通过有限元模型得到大概率出现失效情况关键截面的应力或挠度值.将响应值和抽样标准值基于式(27)得到用以训练GPR模型的输出数据.

根据可靠指标矢量法和上文中计算得到的各子系统失效模式下的灵敏度系数向量，通过公式(19)得到整个桥梁体系的相关系数矩阵再通过PNET法对其分析求解可得最终的可靠指标为5.608 8，失效概率为1.018 4×10-8.

5.4 桥梁退化模型的建立

在桥梁设计基准期(100年)内以10年为间隔，通过可靠指标矢量法和PNET法得到各个时间节点下的主要失效模式从而得到对应时间节点的体系可靠度指标，见表4.

表4 桥梁体系时变可靠指标

将表4中离散化的结果转化成三次多项式形式，该拟合结果即为海子湖特大桥正常使用极限状态下体系时变可靠指标退化模型.具体函数表达和示意图(见图9)为

β(t)=6.328 4×10-6t3-8.970 3×10-4t2-

1.528 3×10-2t+5.563 7

(28)

图9 体系可靠指标退化曲线

根据桥梁体系可靠指标退化曲线，可得到桥梁的最迟维护建议年限为25年，在该年限内桥梁的性能可以满足规范中最低服务水平要求.

5.5 最优维护策略研究

大跨PC连续梁桥在服役期内由于受到外界不利因素以及材料老化的影响，会出现梁体开裂和下挠的病害现象，若不及时采取相应的维护措施来减缓其性能的退化速率而是任其自由发展将会影响桥梁结构的安全和正常使用，同时对于当地的交通系统来说也是一个重大的隐患.因此针对桥梁可能出现的不同病害情况提出并执行相应的解决措施是必要的，经过归纳整理见表5.

表5 常见病害及维护措施

在桥梁的寿命周期内，保证桥梁满足安全可靠的且不影响正常使用的情况下产生最少的维护成本.相应的优化方程为

(29)

式中：βtarget为桥梁结构的目标可靠度，按规范进行取值.

形成相应的维护策略模型首先需满足如下假定：①相同的维护活动每次执行的持续时间和产生的效果是一样的；②维护效应时间小于维护间隔；③维护周期内可靠指标值的波动不会大于结构初始可靠指标β0；④维护行为出现在结构性能发生衰变之后.

不同维修或加固方法对桥梁服役能力的恢复效果，见表6.

表6 维修加固策略的效果及相应费用

通过适应度函数得到的适应度值是遗传算法中判定基因遗传概率的唯一指标，调用遗传算法工具箱中ranking函数对目标函数值做适应度计算.相应的适应度函数为

(30)

约束条件采取罚函数方法，选定惩罚费用为5 000元/m2.

将遗传算法中的最大遗传代数分别设置为100、200、300和400后得到最优维护成本分别为 10 750，10 100，9 700，9 700元/m2.从最大遗传代数为300的种群开始最优解收敛于9 700元/m2，说明最优维护费用出现在300次迭代次数后的种群.上述遗传代数对应的种群目标函数值、最优解对应的遗传代数下搜索示意图以及海子湖特大桥最优维护曲线见图10～12，最优维护策略见表7.

通过上述遗传算法得到的最优维护策略可知:在寿命周期内满足性能指标的情况下，从26年开始对桥梁结构进行上述措施维护，成本最低，其寿命周期内的维护成本为9 700元/m2.

图10 不同迭代次数下种群目标函数变化

图11 300次迭代后种群最优解搜索示意图

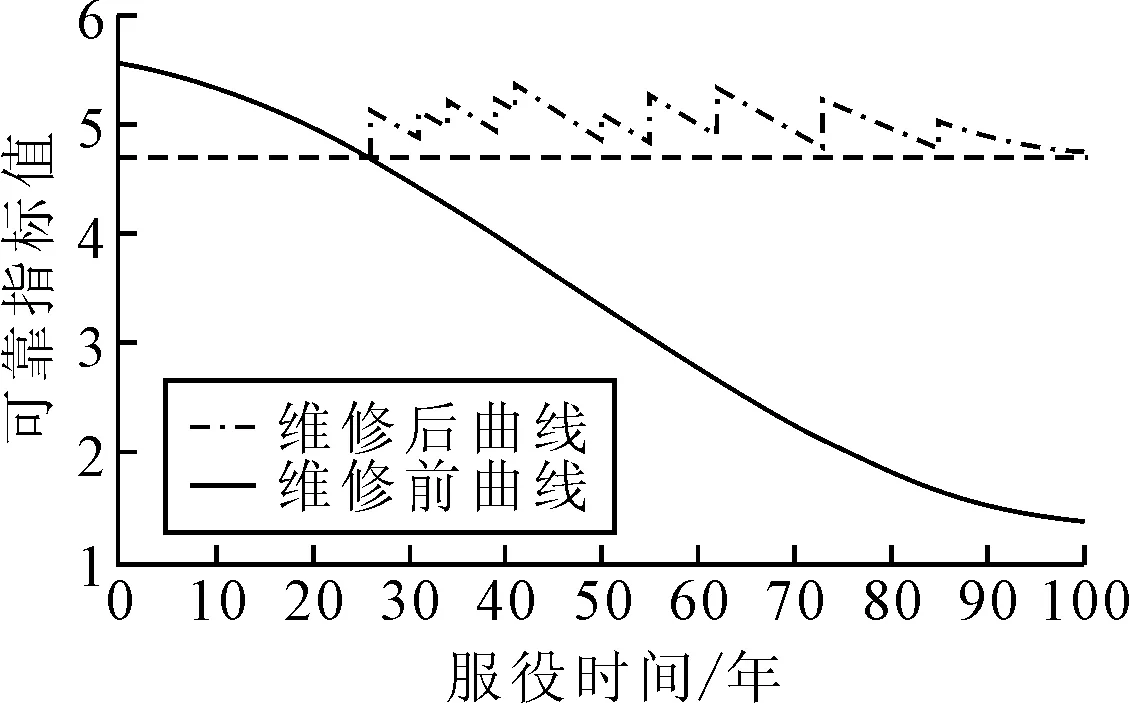
图12 最优维护策略下的可靠指标变化曲线

表7 最优维护策略

6 结 论

1) 将高斯过程回归理论与传统的可靠度方法JC法相结合，同时通过可靠指标矢量法和PNET法来考虑失效模式间的相关性，提出了基于GPR的结构体系可靠度求解方法.索梁算例和工程应用实例均表明本文中采用的分析方法是可行且精确的，对于应对复杂工程中会出现的高度非线性隐式功能函数，且需要对多种失效模式进行相关性分析时，本文方法具备较强的适用性.

2) 基于文中的体系可靠度求解方法，在考虑材料衰变效应的前提下，建立了桥梁的退化预测模型.根据该模型可分析得到，海子湖特大桥的最迟维护建议年限为25年，在该年限内桥梁的性能可以满足规范中服务水平要求.

3) 选用遗传算法对最优维护策略模型求解，最低维护成本在300次迭代后趋于稳定，得到了该桥在100年内满足规范中可靠度指标要求的最优维护方案.