停车换乘设施饱和时刻逐日演化规律研究
梁科科 李葆青 叶 臻 孙 杨
(交通运输部科学研究院 北京 100029)
0 引 言
停车换乘(park & ride,P&R)设施有效缓解了市区停车压力,吸引了大量的郊区小汽车出行者换乘公共交通前往市区[1].然而,由于土地等客观因素限制,P&R设施的停车位供给常年处于供不应求的状态,根据对北京市部分P&R设施的走访调研,发现P&R停车位供不应求是目前十分显著的问题.以某P&R设施为例,在某天清晨的某一时刻达到饱和状态,而在此之后到达的通勤者(P&R使用者)将无位可停;第二天,这部分通勤者将提早出发,以便可以提早到达以保证有位可停,或者干脆放弃使用P&R设施.这就导致了P&R车位的饱和时刻发生变化.如此,P&R设施饱和时刻将随时间day-to-day地不断演化,呈现复杂曲折的逐日动态演化过程.
逐日动态演化问题在交通领域较为常见的是出行者路径选择逐日动态演化问题.有研究指出,出行者的路径选择行为呈现逐日活动规律:出行者第n天的路径选择行为受到第n-1天和之前的行为以及网络状态的影响[2].在该规律的假设前提下,一部分学者利用Agent微观仿真的方法研究演化过程[3-5],另一部分则以非线性动力学为基础,研究平衡的存在性及稳定性[6-8].
可以看出,目前关于P&R设施方面的研究很少关注停车位使用情况,尤其是处于供不应求状态的P&R设施停车位饱和时刻演化规律.而交通领域的逐日动态演化问题很少涉及路径选择和交通流演化以外的情境.文中重点聚焦于P&R设施停车位饱和时刻演化规律,利用非线性动力学理论研究停车位不足条件下的P&R设施饱和时刻逐日演化规律,并讨论平衡点存在性及其渐进稳定条件.
1 问题描述和建模
假设某城市设有一P&R设施(后文称停车场),车位数量(车位供给)为N.每天清晨,陆续有出行者驾驶小汽车到该停车场停车,并换乘公共交通前往市区,而这部分出行者的数量(停车需求)为D.
1.1 模型假设
假设1车位供给小于停车需求:N=ρD,其中0<ρ≤1.
假设2由于路况、信号灯等不确定因素影响,每个出行者到达停车场的实际时刻服从相互独立的随机分布,设出行者第n天到达停车场的实际时刻t(n)服从均匀分布:
F(t(n))=
(1)
式中:μ(n)为第n天的期望到达时刻;L为t(n)的离散程度,L越小,表明出行者的实际到达时刻t(n)可能的取值范围越小.
假设3所有出行者第1天的期望到达时刻均相同,为μ(1).
假设4第n天成功停车的出行者在第n+1天将不调整期望到达时刻,即:μ(n+1)=μ(n).
假设5第n天无位可停的出行者将在第n+1天根据第n天的饱和时刻T(n)调整其期望到达时刻μ(n+1).调整规则为:确保自己第n+1天的到达时刻t(n+1)以一定的概率α早于第n天的饱和时刻T(n)(t(n+1)≤T(n)的概率为α),即满足:
(2)
整理后得:
(3)

1.2 模型推导
由式(1)可以看出F(T,μ)是关于饱和时刻T和期望到达时刻μ的关系式,可以假设:
(4)
式(4)为期望到达时刻为μ的群体在时刻T以前到达的概率.根据假设1、假设2和假设3,可以得到:求第1天的停车位饱和时刻T(1)就是求D个独立同分布的停车需求中,第ρ分位的时刻,即:
(5)
式中:ρ为停车供需比(ρ=N/D),整理得:
(6)
则第2天中,会有比例为1-ρ的出行者无位可停(实际上,每天都会有比例为1-ρ的出行者无位可停),根据假设5,这部分出行者第2天的期望到达时刻将按式(2)调整;根据假设4,其余出行者将不改变期望出行时刻.则第2天的饱和时刻T(2)可由下式求出.
d(2)[(1-ρ)F(T(2),μ(2))+ρF(T(2),μ(1))]=
N=ρD
(7)
如此,便可求出第2天的饱和时刻T(2).第3天又会有比例为1-ρ的出行者按式(2)调整期望到达时刻,而其余出行者中一部分(比例为ρ2)将按照第1天的期望到达时刻出行,另一部分(比例为(1-ρ)ρ)将按照第2天的期望到达时刻出行,而停车需求将变为d(3)=D[T(2)-(T(1)-l)]/l.仿照式(7)便可求得第3天的饱和时刻T(3),如此循环往复,可以看出第n天的饱和时刻T(n)将可由下式求得.
ρn-1F(T(n),μ(1))]=N=ρD
(8)
则第n+1天的饱和时刻T(n+1)将可由下式求得:
ρnF(T(n),μ(1))]=N=ρD
(9)
将式(3)、式(4)带入式(8)和式(9)并整理得:
(10)
(11)
式(10)等号两边同时乘以-ρ并加上式(11)整理得:
(12)
由等比数列求和公式可知:
(13)
将式(13)带入式(12),整理得:
(14)
将d(n)=D[T(n-1)-(T(1)-l)]/l带入式(14),整理得:
T(n+1)=T(n)+
(15)
式(15)为停车位饱和时刻逐日演化模型.第n+1天的停车位饱和时刻与第n天和第n-1天的停车位饱和时刻相关.
特别的,若不考虑假设6,即:停车需求恒为D,则d(n+1)=d(n)=D,式(14)将变为:
T(n+1)=T(n)+L(ρ-α)(1-ρ)
(16)
即:每一天的停车位饱和时刻将呈线性趋势变化.当ρ<α时,线性前移;当ρ>α时,线性后移;当ρ=α时,将维持不变.
2 平衡点求解及其渐进稳定条件
若在某天后,每一天的停车位饱和时刻均相等(不妨设为T*),则称逐日演化达到平衡,该饱和时刻T*即为演化的平衡点,显然地,T*为
T*=T*+
(17)
解得:T*=ρl/α+T(1)-l.下面将讨论平衡点的稳定性问题.
由式(15)可知:该演化模型为一二阶非线性差分方程.关于差分方程解的稳定性问题已有较多研究成果.文献[9]的研究成果给出了如下定理.
定理1二阶非线性差分方程xn+1=f(xn,xn-1)的特征方程为(其中,λ为该差分方程的特征根):
(18)
定理2二阶非线性差分方程xn+1=f(xn,xn-1)平衡点的渐进稳定条件是,平衡点处的特征根的绝对值小于1,即:
|λ(x*)|<1
(19)
根据定理1,式(15)的特征方程可以写成下式(将T*=ρl/α+T(1)-l带入):
(20)
解得:
(21)
根据定理2,平衡点的渐进稳定条件为
-1<λ=
(22)
由于ρ、L、l和α均为大于0的实数,故而式(22)等价于:
(23)
式(23)为停车场饱和时刻逐日演化系统平衡点渐进稳定条件.
3 数值实验
在某城市外围设有一P&R设施,停车供需比ρ=0.8;第1天的停车位饱和时刻为T(1)=480(清晨08:00);出行者到达时刻的不确定性参数L=20(到达时刻在20 min的区间内均匀分布);通过式(6)推算出第1天每个出行者第1天期望到达时刻均为μ(1)=474(清晨07:54);出行者最早允许时刻T′的分布区间长度l=60(即:最早允许时刻T′在清晨07:00—08:00区间均匀分布);调整参数α=0.99(即:第n天无位可停的出行者在第n+1天要确保99%的概率早于前一天).利用matlab进行仿真,结果见图1a).将停车供需比调整为ρ=0.15,维持其他参数不变,再次进行仿真,结果见图1b).

图1 P&R设施饱和时刻随时间变化趋势
由图1a)可知:当ρ=0.8时,在演化初期(n≤40),P&R设施饱和时刻T随着时间推移而不断前移,变化趋势逐渐放缓,直至稳定在468.5(清晨07:48左右),这与通过式T*=ρl/α+T(1)-l计算得到的结果相一致.将各参数取值带入式(23)得到:λ1=0.939<1、λ2=-0.348>-1,满足渐进稳定条件,与仿真结果一致.
与图1a)不同的是随着时间的推移,饱和时刻并不会稳定在某一点,而是发生周期震荡的现象(在426.3~436.5循环往复,即:每天的饱和时刻在07:06—07:16间隔出现).此情况下的特征根计算结果为λ1=0.232<1、λ2=-1.410<-1,不满足渐进稳定条件,这亦与仿真结果一致.
在其他参数给定的情况下,可以通过式(23)计算得到使演化结果渐进稳定的停车供需比ρ需满足的条件:ρ>0.196.图2为饱和时刻最终演化状态与停车供需比ρ之间的关系.
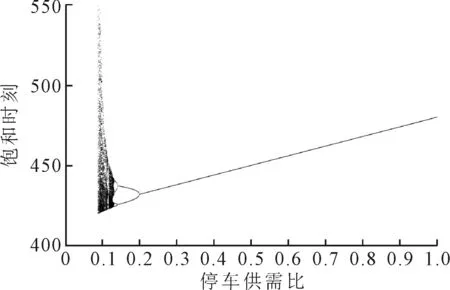
图2 演化最终状态与停车供需比ρ之间的关系
由图2可知:
情况1当ρ>0.196时,饱和时刻最终演化结果趋近于平衡点,并渐进稳定,且随着ρ的增大而逐渐推迟,特别的当ρ=1时,P&R设施的停车位供给完全满足出行者停车需求,饱和时刻将始终维持在最初的时刻T(1)=480(清晨08:00).
情况2随着ρ降低,最终演化结果将出现分岔(周期震荡),且振幅随ρ降低而增大.
情况3随着ρ继续降低,演化结果将出现混沌现象(貌似无规律的复杂运动形态).
情况4继续降低ρ,由于停车位供给远远小于停车需求,饱和时刻演化将迅速提前,直至某一天m提前至区间[T(1)-l,T(1)]左侧,则所有出行者均不选择使用P&R设施,即:d(m+1)=0,最终演化结果为:P&R设施每天无车停放,永远不会饱和.由于实际情况下,停车供需比不可能很小(出行者明知道车位十分紧张,还坚持要使用P&R设施),所以情况3和情况4很少出现,因此探究重点还是放在情况1(均衡)和情况2(分岔)的临界点讨论,即:演化的渐进稳定条件.
接下来讨论L与演化结果的关系.L为出行者实际到达时刻的不确定程度,L越大,表征不确定程度越高.令L取值从0增大至60时(即:实际到达时刻均匀分布区间从0 min增大到60 min),饱和时刻最终演化结果见图3(ρ=0.8).

图3 演化最终状态与L的关系
由图3可知:当L较小时(L≤53.3),饱和时刻最终演化状态趋于平衡点T*=468.5(清晨07:48),且渐进稳定.而且,由于平衡点为T*=ρl/α+T(1)-l,与L无关,最终的平衡点并不会随L的变化而变化.当L较大时(L>53.3),出现分岔(周期震荡)现象,且振幅随L增大而增大.显然地,L的临界点(L=53.3)也可以通过式(23)求得.
4 结 论
1) 当P&R设施停车位数量小于每天的潜在停车需求时,存在一个“饱和时刻”,该时刻停车场停车数量等于车位数量,后续到达的用户将无法停车.
2) P&R设施每天的停车饱和时刻存在逐日演化规律,该规律可以利用非线性动力学模型进行描述.
3) P&R设施饱和时刻逐日演化存在唯一的平衡点,且在一定的条件下渐进稳定.
4) 当停车供需比较高时,演化结果趋向于平衡点,且渐进稳定,平衡时刻随停车供需比降低而提前;当停车供需比较低时,演化结果可能出现分岔(周期震荡)、混沌或趋于无穷等不稳定情况.
5) P&R设施饱和时刻逐日演化平衡点的稳定性受出行者到达时刻分布的随机性影响,到达时刻随机性较高时,演化结果将出现分岔(周期震荡)现象,且振幅随不确定性增加而增大.
研究成果有利于协助交通管理者分析P&R设施停车位饱和规律,并结合潜在需求特征对P&R停车设施进行科学管控,合理引导出行者理性选择出行方式,避免产生无位可停而被迫开车通勤或选择其他费用较高的停车场的情况产生.为了计算方便,研究假设出行者实际到达时刻服从均匀分布,今后的研究可假设正太分布或采用实际数据拟合等方式建立更符合实际的演化模型;此外,由于某些客观原因,研究未能进行实例验证,未来可选取某一实际P&R设施停车数据进行实例分析,验证模型有效性.

