基于支路元件关联矩阵建模与MPGSA算法的电网故障诊断

倪良华，徐祺文，吴春阳，张东东，吕干云

(南京工程学院，南京 210000)

0 引 言

电网故障诊断的基本任务是电网发生故障后，及时有效地判别出故障元件及切除故障过程，对于缩小停电范围，保障安全调控运行具有重要意义[1]。20世纪80年代以来，国内外学者提出了多种电网故障诊断方法。目前电网故障诊断方法主要包括：专家系统[2]，人工神经网络[3-4]，Petri网[5-6]，解析模型[7-8]，粗糙集理论[9-10]，小波分析[11]和多源信息融合[12]等。专家系统[13]依靠专家的知识可以解决很多复杂的故障问题，但缺陷在于知识库需要及时更新，工作量大，容错性差。人工神经网络[14]具有强大的学习能力，容错性好，鲁棒性强，但是困难在于采集大量优质的样本以及对自身诊断推理过程的解释。Petri网[15]能够定性定量分析故障发生过程，但当故障情况复杂时，由于节点过多容易产生状态空间爆炸。信息融合[16]将开关量和电气量信息融合，避免由于信息缺失导致误诊。基于解析模型的电网故障诊断，将故障问题表示为整数规划问题，是一种基于数学模型的诊断方法[17]，建立目标函数后采用智能算法求解，具有较强的理论依据和数学基础。

传统解析模型以可疑元件的状态作为故障假说，目标函数为求保护与断路器的实际状态和期望状态的最小偏差[17]。文献[18]分析了解析模型诊断结果不唯一的原因，考虑主、后备保护之间状态关系对目标函数的共同影响，提出改进的解析模型；但没有针对可疑故障母线和线路分别建模，容易遗漏与可疑故障母线关联的远后备保护，造成误解的后果。文献[19]系统地计及保护和断路器发生误动或拒动的情况，在故障假说中引入保护和断路器误动或拒动的信息，并更新了保护和断路器期望状态的计算公式；但该模型没有考虑主、后备保护之间的配合关系，会造成多解的后果。提出一种改进解析模型，在故障假说中引入保护和断路器发生误动或拒动的信息，并针对母线和线路分别建模，同时引入修正因子避免诊断结果不唯一，能有效识别警报出现误报或漏报的情况。

为了实现解析模型目标函数的自动建模，文献[20]从系统拓扑结构出发，以系统关联矩阵为基础，利用保护、断路器与系统元件之间的拓扑映射关系，对各类保护及断路器的期望状态进行整体建模，实现方便但矩阵运算复杂。文献[21]采用离线建模的方法，根据网络结构列举与停电区域内元件关联的元件及关联路径，针对不同的故障场景需要进行大量重复工作，适用性差。深入挖掘电网各元件之间的拓扑关联关系，提出基于支路元件关联矩阵的自动建模方法，对于不同的电网结构及故障场景应用性强。采用改进模拟植物生长算法MPGSA(Modified Plant Growth Simulation Algorithm)对IEEE 14节点系统的故障场景进行仿真，验证了所提模型与方法的有效性和容错性。

1 改进解析模型

在故障假说H中加入与可疑元件关联的保护和断路器误动或拒动的信息，且在目标函数中引入修正因子，避免多解误解的情况。故障假说基本形式为H=[S,F,M]。

其中S=[s1,...,sk,...,sn]；sk=1/0表示可疑元件k故障/正常；F=[fr1,...,frk...,frnr,fc1,...,fck,...,fcnc]；fri(cj)=1/0表示保护ri(断路器cj)误动/正常；M=[mr1,...,mrk,...,mrnr,mc1,...,mck,...,mcnc]；mri(cj)=1/0表示保护ri(断路器cj)拒动/正常；nr(nc)表示与可疑元件关联的保护(断路器)数量。

电网故障诊断就是找到最能解释告警信息的故障假说，而故障假说可分为合理的故障假说和矛盾的故障假说，例如保护ri既误动又拒动就是一种矛盾的故障假说，即fri=1且mri=1。在合理故障假说的基础上，建立如式(1)的目标函数:

E(H)=w1E1(H)+w2E2(H)

(1)

其中：

E2(H)是故障假说中误动和拒动的保护和断路器的数量之和，E2(H)越小，即误动和拒动的保护和断路器总数越少，目标函数越小，故障假说H越可信。权值w1>>w2，取w1=100。

2 基于支路元件关联矩阵自动建模

以一个4条线路，4条母线的简单电力系统为例，其网络结构与保护配置如图1所示。

图1 简单电力系统结构及保护配置图

2.1 支路元件关联矩阵和元件关联保护矩阵

对于图1简单电力系统，建立支路元件关联矩阵如图2(a)所示。矩阵中第1列为线路名称，第2(3)列为线路送端(受端)断路器名称，第4(5)列为线路送端(受端)连接母线名称。该矩阵隐含了电力系统中元件之间的拓扑关系，通过扫描搜索就能方便地得到元件之间的连通关系。

图2(b)为支路元件状态矩阵，将图2(a)支路元件关联矩阵中的元素置换为对应元件和断路器的状态即可得矩阵(b)。矩阵中第一、四、五列元素为元件状态，1表示故障，0表示正常；第二、三列元素为断路器状态，1表示动作，0表示闭合。

图2(c)为断路器保护关联矩阵，矩阵行数为断路器数量，矩阵列数为4。矩阵中每一行元素为保护的名称，该行保护均以该行对应断路器为出口，由系统保护配置图得到。

图2(d)为母线关联保护矩阵，矩阵行数为母线数量，矩阵列数随网络结构动态变化。矩阵中每一行元素为与该行母线关联的保护名称，第一列为母线主保护，其他列为与该行母线关联的后备保护。

图2(e)为线路关联保护矩阵，矩阵行数为线路数量，矩阵列数随网络结构动态变化。矩阵中每一行元素为与该行线路关联的保护名称，第一列至第六列为线路本身配置的保护，其他列为该线路的关联远后备保护。

图2的关联保护矩阵(d)、(e)可通过搜索支路关联矩阵(a)得到。

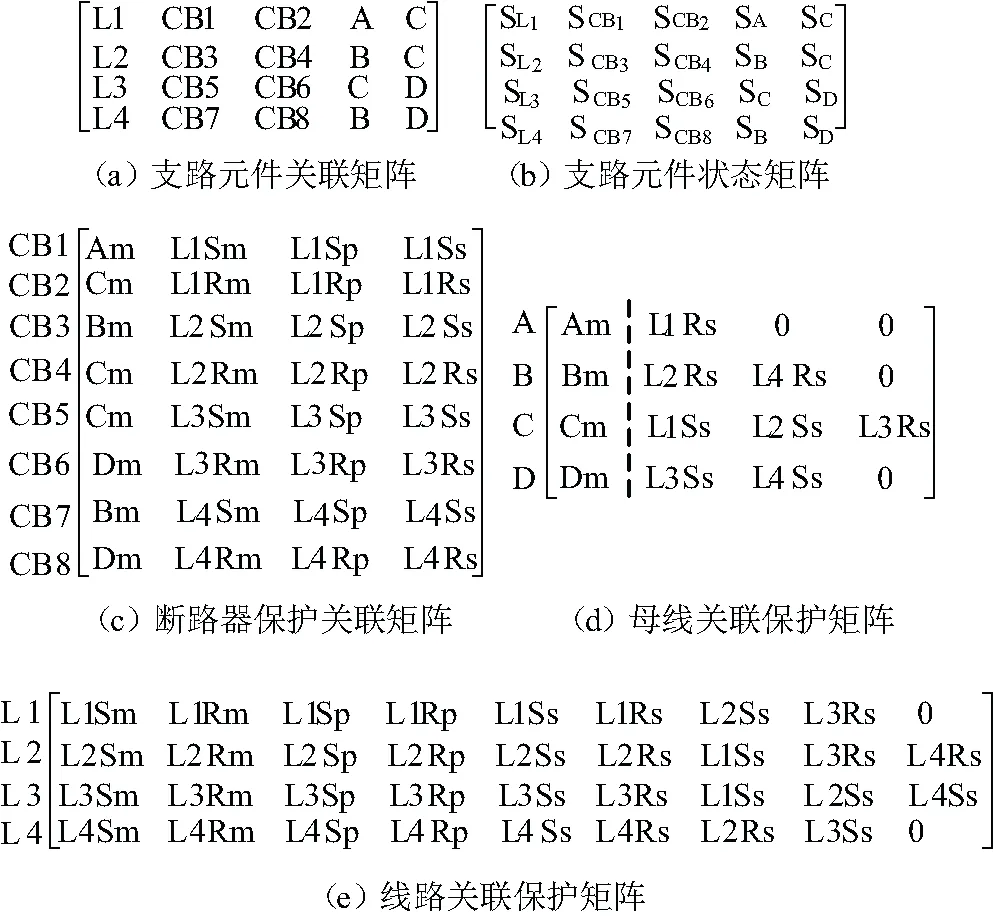
图2 简单电力系统的矩阵描述

2.2 建模过程

针对可疑元件建立目标函数，难点在于如何查找到与可疑元件关联的保护和断路器，以及如何求取关联保护和断路器的期望状态。

2.2.1 搜索可疑元件关联保护和断路器

(1)母线关联保护矩阵生成。

与母线关联的保护不仅有母线主保护，还有与母线直接相连线路的远后备保护作为该母线的后备保护，母线主保护由系统保护配置得到。搜索矩阵(a)得到与母线关联的后备保护(即矩阵(d)虚线之后的保护)的基本步骤为：

步骤1：逐行搜索矩阵(a)找到某母线所在位置；

步骤2：若该母线位于矩阵(a)的第4列，则该母线所连线路的受端远后备保护为该母线的后备保护；若该母线位于矩阵(a)的第5列，则该母线所连线路的送端远后备保护为该母线的后备保护；将搜索得到的该母线后备保护名称自动添加至矩阵(d)该母线所在的行；

步骤3：转至步骤1直至搜索完所有母线为止。

举例搜索母线C的后备保护过程如图3所示。逐行搜索矩阵(a)，得到C位于第1行第5列、第2行第5列、第3行第4列，由线路远后备保护动作原理知L1Ss、L2Ss和L3Rs为母线C的后备保护。母线C关联的保护有{Cm | L1Ss，L2Ss，L3Rs}。

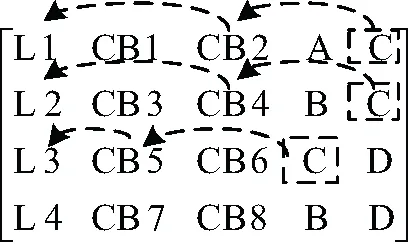
图3 搜索母线关联后备保护过程

(2)线路关联保护矩阵生成。

与线路关联的保护不仅有线路本身的保护，还有与该线路相连的相邻线路的远后备保护，线路本身的保护由系统保护配置得到。搜索矩阵(a)得到相邻线路远后备保护(即矩阵(e)虚线之后的保护)的基本步骤为：

步骤1：逐行搜索图2矩阵(a)，得到某线路所连接的送端和受端母线名称；线路所连送端母线为该线路所在行的第4列元素，线路所连受端母线为该线路所在行的第5列元素；

步骤2：搜索矩阵(d)，得到该线路所连的送端和受端母线的后备保护名称，自动添加至矩阵(e)该线路所在的行，删除重复的元素；

步骤3：转至步骤1直至搜索完所有线路为止。

搜索线路L4的后备保护过程如图4所示。逐行搜索矩阵(a)，得到L4送端连接B，受端连接D。再搜索母线关联保护矩阵得到B和D关联的后备保护。线路L4关联的保护有{L4Sm，L4Rm，L4Sp，L4Rp，L4Ss，L4Rs | L2Rs，L3Ss}。

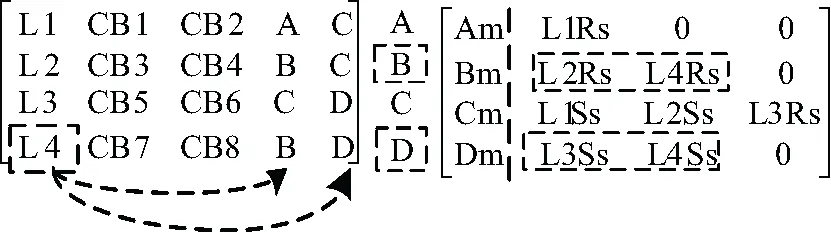
图4 搜索线路后备保护的过程

需要指出的是，由于电网结构的复杂性，矩阵(d)和(e)每一行的维度是动态变化的。根据电网结构建立支路元件关联矩阵，通过搜索该矩阵得到元件关联保护矩阵，可快速地获取与可疑元件关联的保护信息。

(3)可疑元件关联断路器集合。

获取该集合的基本步骤为：

步骤1：在图2矩阵(d)或(e)中扫描可疑元件所在行，得到可疑元件关联的保护集合；

步骤2：在矩阵(c)中逐一搜索步骤1所得的关联保护所在位置，得到可疑元件关联的断路器集合；

矩阵(c)中搜索L4关联断路器的示意图见图5。由图5可得线路L4关联的断路器为{CB4，CB5，CB7，CB8}。

图5 搜索关联保护的出口断路器的过程

2.2.2 未计及误动拒动信息的期望状态表达

元件主保护及近后备保护期望均与路径上的断路器状态无关，断路器期望状态在所有有关的保护期望状态求得后容易得到。线路远后备保护的期望状态与本线路状态、末端母线状态、直接相邻线路状态均有关。各类保护和断路器的期望状态求取表达式可参照文献[20]，由于远后备期望求取过程中涉及关联路径，因此仅针对远后备保护期望作详细论述。考虑远后备保护的不同保护范围，自动求取线路远后备保护的基本思路为：

(1)保护本线路时，线路远后备保护期望状态为：

a1=srks⊗mrksm⊗mrksp

(2)

式中srks为远后备保护rks所保护的本地元件的状态，mrksm(mrksp)为以rks为远后备保护的主保护(近后备保护)是否拒动的状态。

(2)保护末端母线时，搜索图2矩阵(a)得到路径上的断路器名称。若所求保护为线路送端远后备保护，其末端母线为该线路所在行的第五列元素，路径上的断路器为该线路所在行的第三列元素；若所求保护为线路受端远后备保护，其末端母线为该线路所在行的第四列元素，路径上的断路器为该线路所在行的第二列元素。在搜索找到元件和断路器在矩阵(a)中的位置后，对应状态为矩阵(b)相同位置的元素值。其期望状态为：

(3)

式中sj为线路末端母线的状态；cjrks为线路到末端母线的路径上断路器的状态。

(3)保护所连线路时，搜索图2矩阵(a)得到路径上的断路器名称。若所求保护为线路送端远后备保护，先搜索到其末端母线并得到路径上的断路器，再从末端母线出发搜索到末端母线连接的其他线路并得到路径上的断路器，若所求保护为线路受端远后备保护，搜索方法相似不作赘述。若有多条线路，则分别求期望后再求或。其期望状态为：

(4)

式中sl为线路所连线路的状态；clrks为线路到所连线路的路径上断路器的状态；Z(rks)为保护rks的保护范围内的线路集合。

综上，三种情况只要发生其一，线路远后备保护都应动作，因此线路远后备保护期望状态为：

a=a1⊕a2⊕a3

(5)

以求保护L4Ss期望为例，根据远后备保护的不同保护范围，说明如何自动求取线路远后备保护期望状态。

(a)L4Ss保护本线路。

当且仅当线路L4发生故障，主保护L4Sm和近后备保护L4Sp均未有效动作，由远后备保护动作切除本线路故障。L4Ss期望状态表达式为：

aL4Ss=sL4⊗mL4Sm⊗mL4Sp

(6)

式中符号含义同式(9)。

(b)L4Ss保护本线路末端母线。

当且仅当母线D发生故障而母线主保护Dm未有效动作导致CB8拒动，由L4送端远后备保护动作跳开CB7切除故障。从拓扑矩阵中看到，从L4的送端到达D，路径上断路器有CB8。搜索路径如图6(a)所示。

L4Ss期望状态表达式为：

aL4Ss=sD⊗(1-sCB8)

(7)

式中符号含义同式(10)。

(c)L4Ss保护本线路直接下游线路。

当且仅当本线路相连线路L3发生故障而故障线路本身的保护未及时动作，由L4送端远后备保护动作切除故障。从拓扑矩阵中看到，从L4的送端到达L3，路径上断路器有CB8和CB6。搜索路径如图6(b)所示。L4Ss期望状态表达式为：

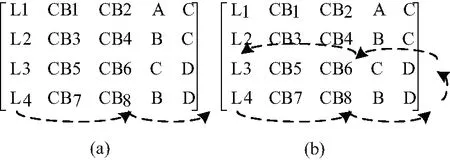
图6 L4送端搜索关联元件的路径

aL4Ss=sL3⊗(1-sCB8)⊗(1-sCB6)

(8)

式中符号含义同式(11)。

综上L4Ss期望状态表达式为：

aL4Ss=(sL4⊗mL4Sm⊗mL4Sp)⊕(sD⊗(1-sCB8))⊕(sL3⊗(1-sCB8)⊗(1-sCB6))

(9)

2.2.3 计及误动拒动信息的期望状态表达

将所有未计及保护和断路器误动与拒动信息的期望状态记作ari(H)和acj(H)，在此基础上，针对合理的故障假说，考虑故障假说中的fri、mri、fcj和mcj，过程见表1。最终确定计及保护和断路器误动与拒动的期望状态表达式如下：

表1 保护和断路器的期望状态计算

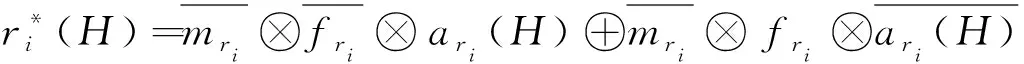
(10)

(11)

3 改进模拟植物生长算法(MPGSA)

模拟植物生长算法(PGSA)于2005年由李彤等提出[22]，通过建立人工植物，模拟植物的“向光性动力机制”，是一种求解整数规划问题的仿生类通用概率搜索算法。针对整数规划求解的特点，建立了四个基本概念：树根、树干、树枝、生长点。树根即整数规划的初始可行解x0，生长点是植物的生长细胞，模拟植物每一次生长的位置点，由生长点沿2n方向，以dx为步长生长形成新枝，树枝和树干是分别由初始状态x0和生长点沿2n方向生长组成的可行域空间。

生长点是否长出新枝由生长细胞的形态素浓度决定，新的生长点产生后，形态素浓度将根据新环境重新进行分配。设树干长度为M，上面有K个初始生长点SM=(SM1,SM2,…,SMK)，每个生长点的形态素浓度为PM=(PM1,PM2,…,PMK)；设树枝长度为m，上面有q个新生长点Sm=(Sm1,Sm2,…,Smq)，每一个生长点的形态素浓度为Pm=(Pm1,Pm2,…,Pmq)，树干及树枝上各生长点的形态素浓度值为：

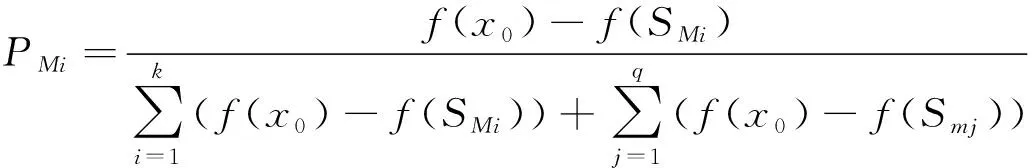
(12)

(13)

式中的x0为初始可行解；f(·)为目标函数值。树干和树枝上k+q个生长点对应k+q个形态素浓度值，每次产生新枝形态素浓度值都将发生变化。

为解决PGSA生长点劣化和生长空间过大的问题，提出改进生长点淘汰机制，具体改进如下：

(1)将随机数选中的生长点作为下一次生长过程的实际生长点，同时将可生长点集合中形态素浓度值低于此点的生长点淘汰；

(2)改进形态素浓度计算公式，用于计算第n次生长后仍未被淘汰的优质生长点的形态素浓度：

(14)

(15)

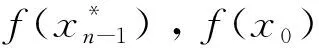
改进生长点淘汰机制后的MPGSA步骤如图7所示，图中虚线框内为改进部分。

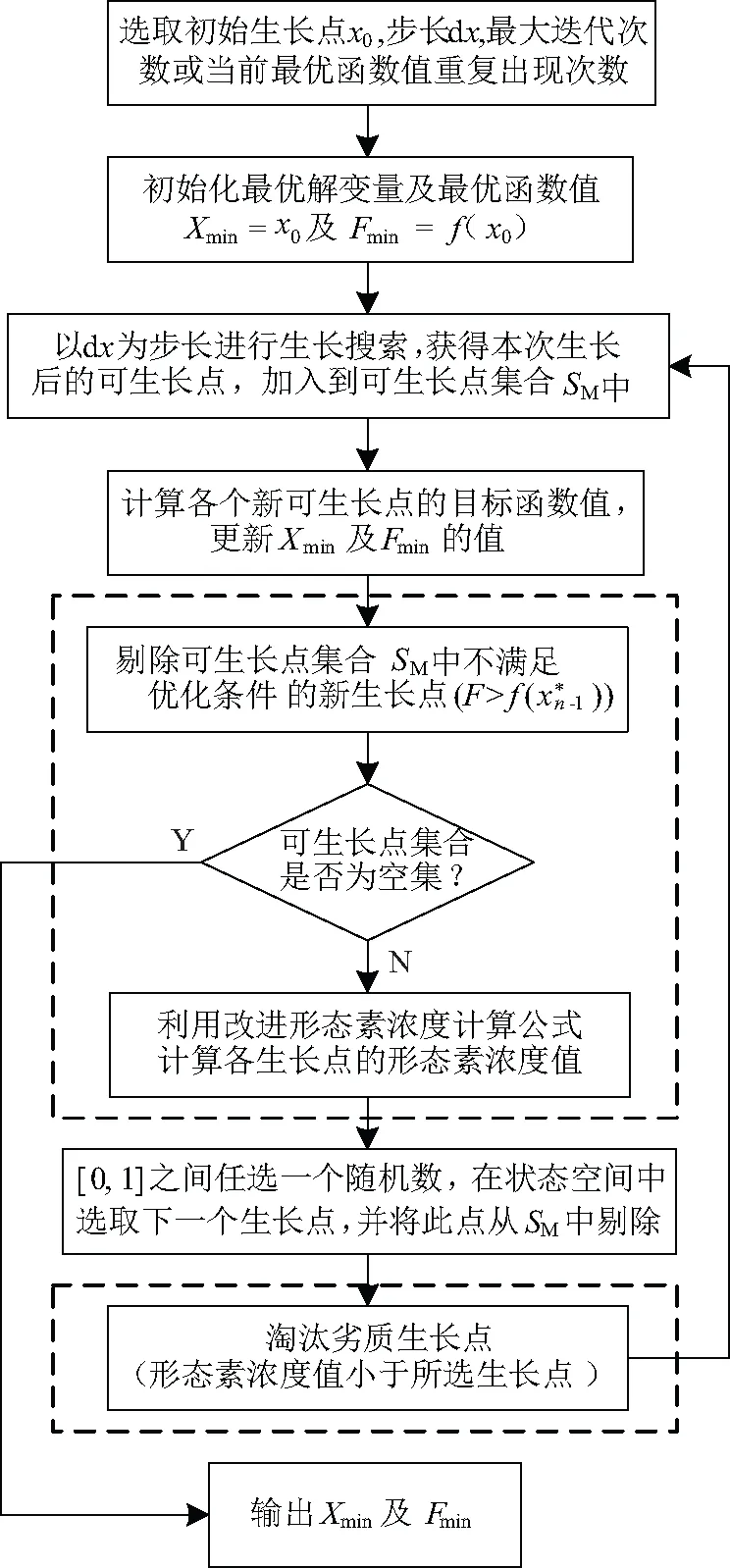
图7 MPGSA算法流程图

改进生长点淘汰机制的优点为：在保留PGSA随机概率的优势前提下，淘汰每次生长过程中产生的劣质生长点，缩小生长空间，提高了优质生长点被选中的概率，提高了算法的优化效率；随着可生长点集合中的生长点不断被淘汰，新生长点不出现更优值，可生长点集合变为空集，此时选中的生长点即为最优解，从而提供一种新的终止判断机制。

4 故障诊断流程

故障诊断流程见图8。

图8 故障诊断流程图

主要步骤如下：

步骤1：由SCADA得到告警信息，根据结线分析法确定可疑元件；

步骤2：根据网络拓扑结构建立支路元件关联矩阵，通过搜索支路元件关联矩阵得到断路器保护关联矩阵和元件关联保护矩阵；

步骤3：在母线关联保护矩阵和线路关联保护矩阵中搜索可疑元件所在行，确定与可疑元件关联的保护集合；在断路器保护关联矩阵中搜索关联保护所在位置得到可疑元件的关联断路器集合；建立故障假说H={S,F,M}；

步骤4：采用第2节自动建模方法自动求得关联保护和断路器的期望状态，并得到目标函数；

步骤5：采用第3节MPGSA算法求解，得到正确的故障假说Hbest={Sbest,Fbest,Mbest}；

步骤6：由正确的故障假说可得到真实的故障元件，以及误动或拒动的保护和断路器信息；

步骤7：根据正确的故障假说，求出对应的保护和断路器的期望状态；

步骤8：将正确的故障假说对应的保护和断路器的期望状态与告警状态对比，得到漏报或误报的告警信息。

5 算例分析

采用MATLAB开发工具IEEE 14节点系统进行故障诊断测试，验证所提出的方法及模型的有效性，实验结果列于表2中。IEEE 14节点系统如图9所示。

图9 IEEE 14节点系统

表2 IEEE 14节点系统案例诊断结果

以案例5为例详细说明所提故障诊断方法。告警信息{B7m，B10m，L18Rs，CB13，CB15，CB18，CB36，CB40}，由结线分析法，得可疑故障元件结合S={B7，B10，L18}，记为S={s1,s2,s3}；通过搜索母线关联保护矩阵和线路关联保护矩阵，得到与可疑元件关联的保护如表3所示。

由表3可知，与可疑元件关联的保护为{B7m，B10m，L18Sm，L18Rm，L18Sp，L18Rp，L7Rs， L8Rs，L9Rs，L14Ss，L18Ss，L18Rs，L20Ss }，记为{r1～r13}；通过搜索断路器保护关联矩阵，得到所有关联的保护出口的断路器集合为{CB13，CB14，CB15，CB16，CB17，CB18，CB27，CB35，CB36，CB39，CB40}，记为{c1～c11}。建立故障假说如下：

表3 案例5中可疑元件关联的保护

H=[s1～s3,fr1～fr13,fc1～fc11,mr1～mr13,mc1～mc11]

根据第2节方法自动建模得到优化模型，用MPGSA算法求解，得到最优解为：

H=[1, 1, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 1, 0, 0, 0]。

由最优解看到：

[s1,s2,s3]=[1,1,0], 即真实故障元件为B7和B10；

[fr1,fr2,...,fr13]=[0,0,...,0]，即关联保护没有发生误动；

[fc1,fc2,...,fc11]=[0,0,...,0]，即关联断路器没有发生误动；

[mr1,mr2,...,mr13]=[0,0,...,0]，即关联保护没有发生拒动；

[mc1,mc2,...,mc11]=[0,0,...,1,0,0,0]，即断路器CB35发生拒动。

根据诊断结果结合告警信息，可推理出案例5的故障切除过程为：B7和B10发生故障，B7m动作跳开CB13、CB15和CB18，B10m动作跳开CB35和CB40；但CB35拒动，导致没有成功切除故障母线B10，随即下游线路远后备保护L18Rs动作跳开CB36。

提出的模型及方法，当存在保护和断路器误动或拒动的情况时，诊断出的真实故障元件与文献[16]相同，可见其适用性与准确性；且告警信息评价更加准确，提高了容错性。

6 结束语

提出的电网故障诊断改进解析模型针对母线和线路分别建模，考虑了母线关联的后备保护对目标函数的影响，引入修正因子消除相关保护拒动造成的不利影响，并且加入故障假说最小化指标，诊断结果唯一且正确。提出的以支路元件关联矩阵为基础的自动建模方法，应用于不同规模的电网故障诊断，适用性强。利用改进生长点淘汰机制的模拟植物生长算法(MPGSA)求解解析模型，在计及误动、拒动、误报、漏报的情况下依然有较好的容错性和鲁棒性。IEEE 14节点算例仿真结果论证了所提故障诊断方法的有效性。