基于S-LCL补偿的磁场感应式电能传输系统研究

徐紫薇，李晓明，杨林，董子凡

(武汉大学 电气与自动化学院， 武汉 430072)

0 引 言

近年来，无线电能传输(Wireless Power Transfer, WPT)技术以其安全、方便、可移动性强、环境适用性强、无积尘和无接触损耗等优点[1]，逐渐成为电力电子领域的研究热点。根据电能传输机制的不同，WPT技术主要可分为电磁辐射式[2]、磁场耦合式[3-5]、电场耦合式[6]和超声波式[7]。磁场耦合式WPT技术又可分为磁场感应式电能传输(Inductive Power Transmission，IPT)[8]和谐振式电能传输技术[9]。其中IPT技术是目前技术最为成熟且最具发展前景的无线电能传输技术之一。IPT技术目前已被广泛应用于短距离(毫米至厘米级)的电能传输场合[10]，如电动汽车锂电池的充电、便携式电子产品的供电[11]、发光二极管的驱动电路[12]、植入式医疗设备[14]的供电等。

IPT系统的负载通常都是动态变化的，在某些特定的运用场合下，IPT系统需提供不受负载变化所影响的恒定电压或电流输出。目前，主要有两种方式来实现IPT系统的恒定电压或电流输出：(1)基于控制策略的IPT系统设计方法；(2)基于补偿电路拓扑的IPT系统设计方法。基于控制策略的IPT系统设计方法又称为动态调节法[14]，主要可分为：变频控制(Frequency Conversion Control，FCC)[15-16]、相移调制(Phase Shift Modulation, PSM)[17]，以及直流-直流变换[18-19]。虽然以上三种动态调节法可以实现较为精确的恒流、恒压输出，但是PSM技术难以保证高频逆变器实现零电压开关(Zero-Voltage Switching, ZVS)运行；FCC技术在负载电阻变化较大的情况下，会产生频率分叉现象，从而降低系统的稳定性与可靠性[20]；直流-直流变换器的引入增加了系统的重量、体积、成本以及相关的电能损耗。为减化IPT系统的控制方案，越来越多的研究人员将目光投向基于补偿电路拓扑的IPT系统设计方法，即通过在电路中增加电容、电感等补偿元件，合理设计电路拓扑与系统参数，利用电路的自身特性来实现系统电流、电压的恒定输出。

IPT系统补偿电路的拓扑结构包含四种基本类型：串联-串联(S-S)结构，并联-并联(P-P)结构，串联-并联(S-P)结构以及并联-串联(P-S)结构。其中，基于P-S结构和P-P结构的IPT系统需由电流源型逆变器供电，而电流源型逆变器所占空间较大，因此这两种拓扑结构的运用具有较大局限性。而S-S结构和S-P结构则分别适用于恒流输出和恒压输出的场合，且均能实现零相位角(Zero Phase Angle, ZPA)运行[21]。传统的二阶补偿电路具有结构简单、成本低、占用空间小等优点，但是由于具有较低的设计自由度，一旦确定了松耦合变压器线圈的自感大小，系统的输出电流或电压则无法被改变。为解决这一问题，许多文献提出了具有更高自由度的高阶补偿电路。文献[22-24]提出了能够实现恒流输出的双LCL拓扑结构。双LCL结构可以看作在P-P结构的基础上在接收侧和发射侧各增加了一个串联补偿电感，为满足双LCL补偿网络的谐振条件，其发送侧与接收侧的补偿电感大小都设置为与主电感大小相等，这增加了系统的体积与成本。文献[25-27]提出了基于双LCC结构的IPT系统，该结构同样能在ZPA运行条件下实现恒流输出，且与双LCL结构相比，双LCC结构在主电感支路中添加了谐振电容，这一设计能够减小系统补偿电感的大小，从而降低系统的成本与体积。然而，双LCC补偿电路一共具有六个补偿元件，电路结构与参数设计都较为复杂。

为解决上述高阶补偿电路存在的体积大、成本高、所需补偿元件多的问题，文章提出一种基于S-LCL补偿电路的IPT系统。所提出的S-LCL补偿电路能够在近似ZPA输入与ZVS运行的前提下实现变负载条件下的恒流输出，且输出电流不受限于松耦合变压器线圈的自感大小。文章的章节内容安排如下：第1节对基于S-LCL补偿电路的IPT系统进行了等效电路模型的建立与数学推导，得出系统的ZPA条件与恒流输出条件。第2节介绍了系统松耦合变压器的设计和系统参数整定，通过合理的参数整定，系统能在输出恒定电流的同时实现近似ZPA输入与MOSFET的ZVS运行。第3节搭建了实验样机，通过实验证明了理论推导的正确性与文章所提出系统的实用性。

1 基于S-LCL补偿电路的IPT系统理论分析

1.1 S-LCL补偿电路分析

基于S-LCL补偿电路的IPT系统电路拓扑如图1所示。

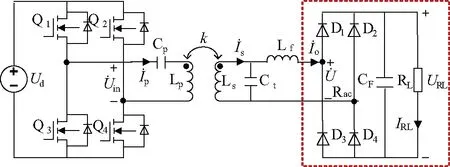
图1 基于S-LCL补偿的IPT系统电路拓扑

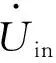
(1)

图1中，Q1～ Q4为四个功率MOSFET,由Q1～ Q4构成的高频逆变器将直流电压转变为交流方波电压。Lp和Ls分别为发射线圈和接收线圈的自感，即发送侧和接收侧的主电感；Cp和Cs分别为发射侧和接收侧的补偿电容，Lf为接受侧补偿电感；k表示发送线圈与接收线圈间的耦合系数；D1～ D4为四个肖特基二极管，由D1～ D4所构成的全桥整流器将接收侧电路中的交流电流转变为直流电流IRL进行输出；CF为输出滤波电容；RL为负载电阻。图1中用虚线圈出的部分可用等效交流电阻Rac来代替，Rac可通过式(2)计算得到：

(2)

为了简化分析，文章引入阻抗变量ZM、Zp、Zs、Zt、Zf。其表达式如下：

(3)

图2为系统的互感等效电路。

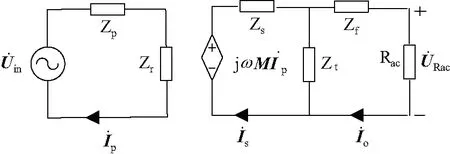
图2 基于S-LCL补偿的IPT系统的互感模型

图2中,M为接收侧与发送侧线圈之间的互感值；ω为系统的工作角频率；Zr为接收侧在发送侧的映射阻抗，其表达式为：

(4)

1.2 S-LCL补偿电路的恒流输出条件

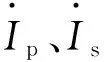
(5)

(6)

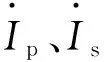
(7)

(8)

可见，为实现与负载无关的恒流输出，需使B=0。根据式(7)可推导出系统的恒流输出条件为：

(9)

1.3 S-LCL补偿电路的ZPA运行条件

根据图2可得到输入阻抗Zin的表达式为：

Zin=Zp+Zr

(10)

将式(3)、式(4)、式(9)代入式(10)，可得到恒流条件下输入阻抗Zin的表达式：

(11)

要实现ZPA运行，即使Zin呈纯阻性，需满足：

(12)

将式(12)代入式(11)，可将输入阻抗Zin进一步表示为：

(13)

将式(7)、式(9)和式(12)代入式(8)，可将跨导G进一步表示为：

(14)

从式(13)和式(14)可以看出，当式(9)和式(12)同时成立时，系统输出不受负载变化所影响的恒定电流，并实现ZPA运行。且从式(14)可看出，文章所提出的S-LCL补偿结构可以通过改变电路的补偿参数大小来输出某一特定大小的电流，因此系统的输出电流不受限于松耦合变压器的线圈自感大小。

2 松耦合变压器的设计及系统参数整定

2.1 松耦合变压器的设计

在线圈直径相同的情况下，方形圆角线圈相比普通的圆形线圈具有更大的自感值和互感值，且受到趋肤效应和临近效应的影响更小。因此，文章在设计IPT系统中的松耦合变压器时，发送侧与接收侧线圈都采用方形圆角的设计。系统松耦合变压器的尺寸规格在表1中列出，发送侧与接收侧的间距设置为100 mm。

表1 松耦合变压器的尺寸规格

图3展示了在电磁场有限元分析软件JMAG中搭建的松耦合变压器模型。仿真得到，发送侧线圈与接收侧线圈的自感均为103.4 μH，线圈之间的互感为21.3 μH。

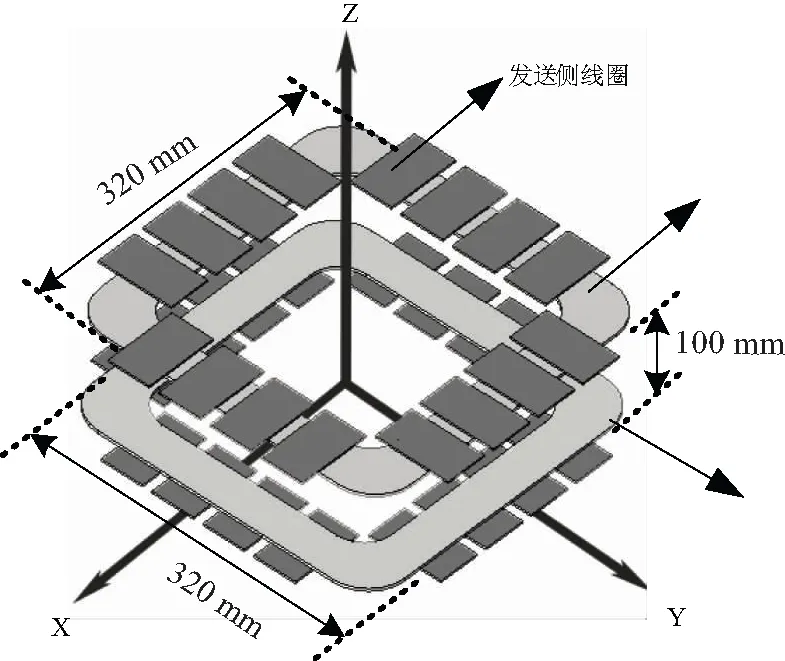
图3 松耦合变压器的有限元分析模型

2.2 补偿元件参数的确定

解一:

(15)

解二：

(16)

由于Zt和Zf的物理意义分别为系统电容Ct和电感Lf的等效阻抗，因此方程组的解必须满足Zt的虚部小于0，而Zf的虚部大于0的先决条件。不难看出，解一能够满足这两个条件；解二中的Zf的虚部恒小于0，不符合条件。因此，解一为方程组的可行解。这说明了从物理上能够实现文章1.2中所提出的恒流条件与ZPA条件。

将式(3)代入式(15)，可进一步求得电路补偿元件Cp、Ct、Lf的值：

(17)

当电路的补偿元件参数Cp、Ct和Lf满足式(17)时，系统可以在ZPA运行条件下，输出指定的电流。文中设定输入直流电压Ud为50 V，输出电流IRL为4 A。由式(16)可以求得三个补偿元件的参数。表2列出了根据上述流程整定得到的系统参数。

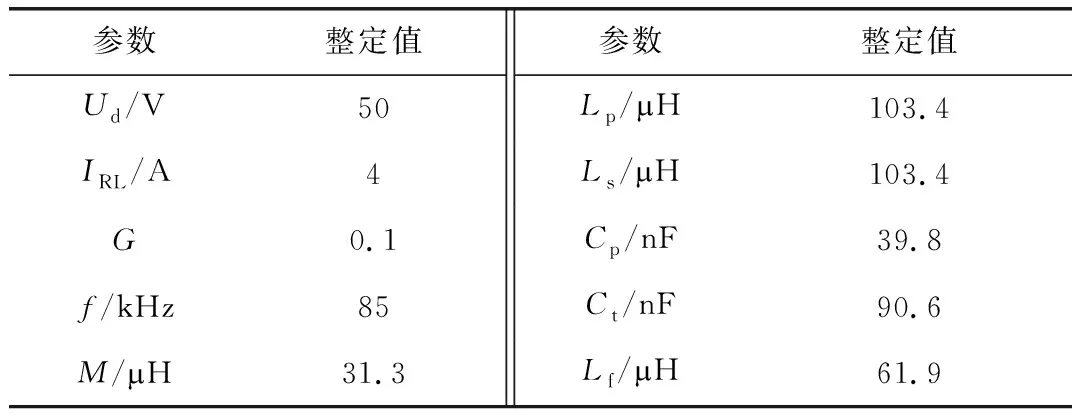
表2 系统参数

2.3 MOSFET零电压开关的实现

由于功率开关MOSFET 具有不可忽略的漏源寄生电容，因此需要对系统补偿参数进行微调，使系统整体略微呈感性，以实现MOSFET的ZVS运行。ZVS的实现有助于降低功率开关MOSFET的导通损耗，从而提升系统的电能传输效率。系统输入阻抗Zin的一般表达式为：

(18)

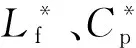
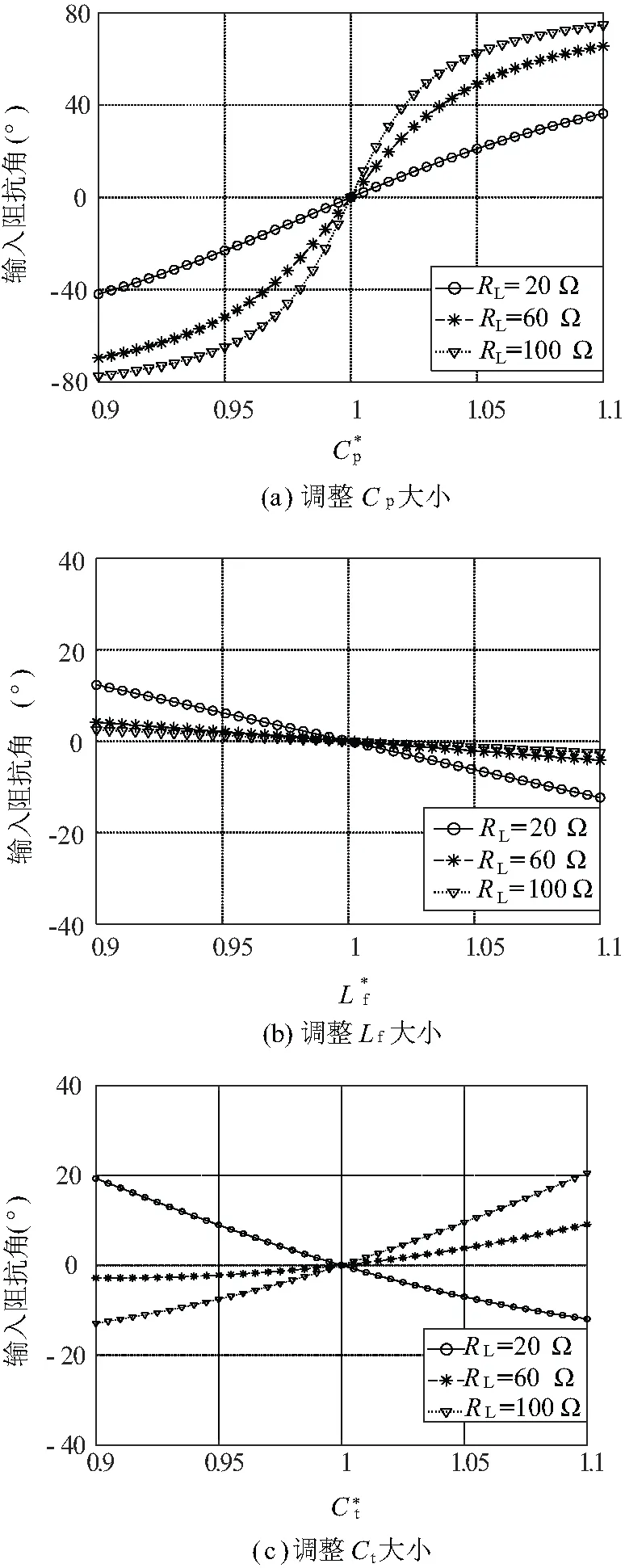
图4 系统输入阻抗角随归一化补偿参数与负载电阻的变化情况

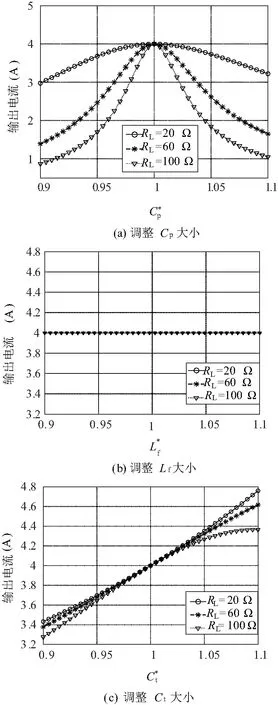
图5 系统输出电流随归一化补偿参数与负载电阻的变化情况

3 实验结果与分析

3.1 实验模型的搭建

图6展示了文章所搭建的基于S-LCL补偿的IPT系统实验样机。

图6 基于S-LCL补偿的IPT系统实验模型

实验样机由直流电压源、高频逆变器、松耦合变压器、发射侧补偿电容Cp、接收侧补偿电容Ct、接收侧补偿电感Lf、全桥整流器、可变负载RL、示波器组成，以上元器件分别在图6中1～9依次进行了标注。其中，高频逆变器由四个具有较低导通电阻的MOSFET构成，全桥不可控整流器由四个快恢复二极管构成。补偿电容选用在高频条件下具有较高载流容量和较低损耗的丙烯薄膜电容器。模型的实际测量参数在表3中列出。

表3 系统参数实际测量值

3.2 实验结果分析

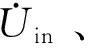
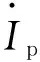
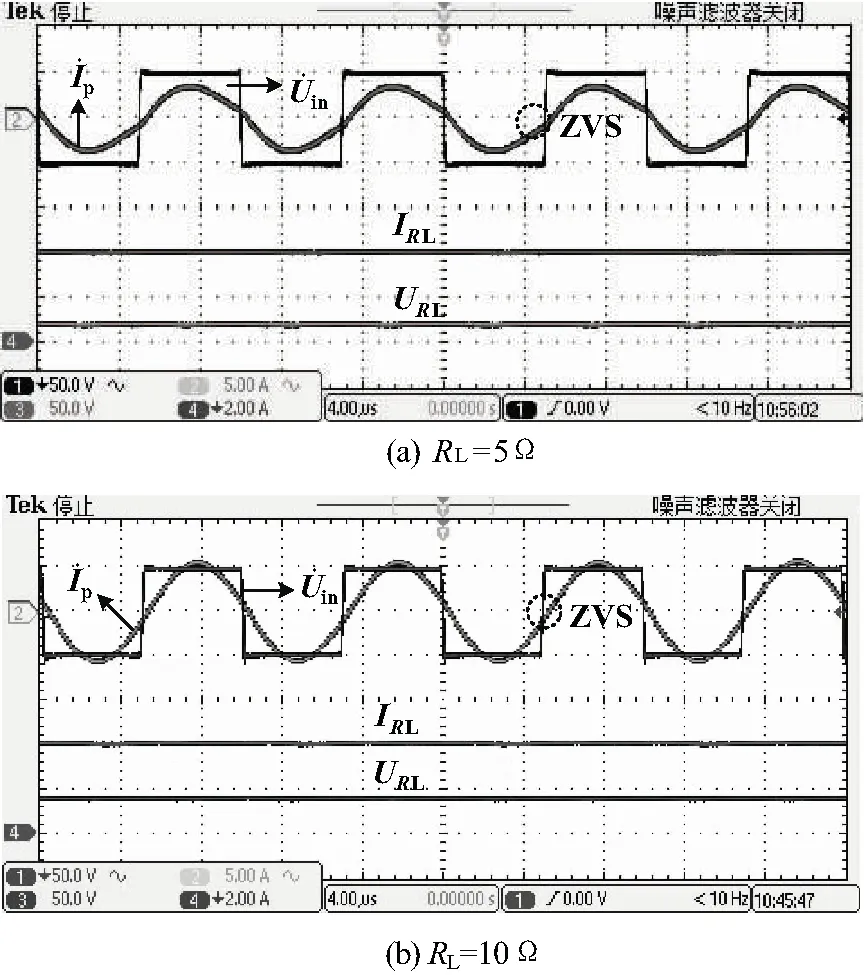
图和IRL的实验波形图

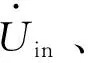
图8 负载电阻突变时的实验波形

随着负载电阻RL变化，IPT系统的电能传输效率也会发生相应变化[28]。图9展示了系统电能传输效率随RL变化的曲线(5 Ω

4 结束语

文章提出了一种基于S-LCL补偿的IPT系统,该系统能输出不受负载变化所影响的恒定电流，且输出电流不受限于松耦合变压器的线圈自感大小。并且系统能够实现近似ZPA输入与MOSFET的ZVS运行。文章建立了系统的电路拓扑以及互感等效电路模型，并通过理论分析推导出使系统实现恒定电流输出与ZPA运行的条件。基于恒流输出和ZPA运行条件，文章给出了基于S-LCL补偿的IPT系统的参数整定方法。此外，文章还分析了系统的补偿参数与输入阻抗角和输出电流的关系，并基于此提出了使功率MOSFET实现ZVS的参数调整方法。最后，文章搭建了一套实验样机，实验结果与理论分析结论相一致，电能传输效率实际测量值的最大值达到92.8%。