基于隐私同态的城市配电网多级网格数据聚合算法

夏伟，蔡文婷，刘阳

(南方电网数字电网研究院有限公司， 广州 510000)

0 引 言

数据聚合是对城市配电网信息综合处理的重要技术手段，通过对数据聚合操作能够降低数据采集过程中的通信费用和能量消耗。但是在数据聚合中没有受到隐私保护，致使配电网数据常出现丢失、篡改现场，因此，在数据隐私保护的基础上，对城市配电网多级网格数据聚合已成为目前亟需解决的问题。

针对该问题，国内外学者研究了数据聚合算法，可以有效聚合城市配电网多级网格数据。其中，文献[1]研究了基于雾计算的智能电网安全与隐私保护数据聚合方法，该方法利用云雾合作的加密算法对数据多层隐私保护，并在雾端对数据进行了多层融合，实现整个网络数据的聚合；文献[2]研究了雾辅助的轻量级隐私保护数据多级聚合方法，该方法利用雾协作方法收集数据，采用模数性质对数据加密，并借助三列函数设计认证方法，实现数据的聚合。但是上述两种算法在进行数据聚合过程中，没有受到隐私保护，导致数据常出现丢失、篡改情况。文献[3]研究了智能电网中的数据聚合方法，结合Paillier加密体制和ElGamal加密体制对智能电网数据进行加密处理，并通过双线性对技术对数据聚合。文献[4]研究了一种缓解能量空洞的数据聚合算法，通过数据聚合的方式使每个节点发送数据时以最大的分片数进行传送，采用节能的方式对WSN能耗进行优化，以减小EH的区域，使全网能耗最低。但是上述两种算法的加密性较差，导致数据聚合时间较长，聚合效率较低。

而隐私同态是一种直接对密文数据进行相关运算的加密技术，能够避免数据融合时隐私信息的泄漏，常应用于在数据聚合方案中。基于隐私同态的这个优点，将其应用到城市配电网多级网格数据聚合中，根据重新获取的数据，并在通过密度阈值函数设置、初始聚类中心选取与网格聚类的步骤下完成城市配电网多级网格数据聚合，并采用隐私同态技术对聚合后的数据进行加密处理。通过仿真实验可知，文中在实现数据聚合的同时，提高了数据的安全性，解决了传统算法中存在的问题。

1 数据重获

在进行城市配电网多级网格数据聚合计算之前，首先要通过电力公司数据库，获取保存在电力公司中的所有数据，以进行数据聚合，包括涉及到的用电资源、网格信息等。虽然数据库中存有大量各类型数据，但与所研究的网格数据相差较大，每个数据的概念与结构也应符合计算需求，因此要在经过处理后的数据库中筛选与文中相匹配的数据。首先，在大数据中找到与公共信息模型可交换的数据，互相融合，得到一个基于公共信息模型(CIM模型)的结构。然后，选择一个最优的链路，在此过程中不断完善数据结构，为配电网系统奠定一个夯实的基础。最后，对重获的数据进行分析，提供一个最佳的聚类方式，保证电网的稳定运行，其这个配电网数据重获的过程如图1所示。

按照图1中的步骤分析，个别数据的交换方式仍然不能全部导入，格式与模型中的结构也互相不统一，致使准确率有些许波动。因此，需要进行格式统一，从而降低数据通信开销。

图1 配电网数据重获过程

2 城市配电网多级网格数据聚合

2.1 城市配电网多级网格划分

城市配电网多级网格映射关系图如图2所示。城市配电网多级网格的划分需综合考虑供电区相对独立性、网格完整性、管理便利性等因素，主要分为高压层、目标网架、中压线路层、配电站层、配变层。

图2 配电网多级网格映射关系图

2.2 密度阈值函数设置

传统的聚类算法是基于数据库完整的情况下进行的，而数据流的聚类是基于数据的聚类算法上的，在其他领域上具有广泛的应用，例如商业互通、网络记录的记录与分析。

对城市配电网多级网格数据空间进行网格单元划分，每个网格单元中，存在多维空间s，将k维为均分成长度相等的dk段，那么在dk段中的数据集合表示为：

sk={sk1,sk2,…,sk}

(1)

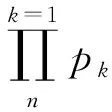
d=(d1,d2,…,dn)∈m

(2)

并且约束条件[4]为：

dk∈skgt,(k=1,…,n)

(3)

式中gt为空间中的网格单元。若整个配电网中网格单元的总数为：

(4)

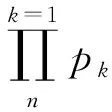
D(m,td)=λtD(m,tb)+1

(5)

式中td为时间。如果数据在时刻ta时进入网格单元，其数据密度就会与时间的改变相关，将其定义为：

D(d,t)=λt-ta

(6)

式中λ为流动系数，且为整数，一般徘徊在0～1，d代表数据，tb代表某一时刻。如果网格单元m中数据的密集程度为D(m,t)，在不同的时刻t与y的分布密度也就不同，分别如下：

(7)

(8)

当网格单元的数据密度满足Di≤D(m,t)，那么就称为密集单元，式中Zt与Zy为常量，且两者的关系为Zt>Zy，如果满足Dy>D(m,t)≤Dt，那么在此条件下的网格单元为替代网格单元，当Dy>D(m,t)时，网格单元就为噪声网格单元[5-7]。

如果噪声单元密度不断增大，在时刻y的密度就远远大于普通网格单元密度，一般都会慢慢消化网格中的密集数据，经过处理，就形成了一个进化的网格单元，叫做进化噪声单元；而剩下的网格单元情况是本来只具有很少的数据，经过慢慢叠加[8]，逐渐演变成噪声网格单元，只有将噪声网格单元减少到最小或是消失，才会实现数据的有效聚合，保留网格数据携带的信息，并且被永久储存。

假设单元m的初始移动时间为ta，最后移动时间为tb，那么两者的密度阈值函数[9]定义为：

(9)

基于以上函数，就可以判断单元是否是噪声网格单元，集合的最小值Dmin按照时间的长短来辨别新增的网格数据，且会随着时间的改变而进行自身优化，经过时间的淘汰[10]，就可以确定密度函数的阈值，当接收到网格数据后，Dmin(tb,ta)的值会立即降到最小，因此利用Dmin(tb,ta)的变化来分析网格单元的类型的方法不但可行且效率最高。

2.3 初始聚类中心的选取

选取聚类中心的目的在于判断数据之间的距离，获取最佳聚类系数，为网格聚类奠定基础。聚类中心的选取主要与系数K相关，利用其均值随机挑选一个初始聚类中心，但其结果容易受到影响，导致结果会处于一个波动的范围，假如以距离为主进行选择，就会出现分贝不同的噪声干扰，聚类的效果并不明显。因此在进行初始聚类中心的选取[11]时，要准确无误地判断数据之间的距离以解决分布的密度问题，从网格数据库中选择，在密集单元里选出一个位移最大的初始K值作为聚类中心[12]，尽量将噪声的干扰降到最低，从而提升算法的运行效率。假设将一个密集单元作为圆心，以数据间最大距离r作为半径，其中包含的圆形区域就叫做r-邻域[13]，按照以往的聚类实践，r的大小通常是数据之间最大距离的二分之一。

设定一个上限阈值为p，那么在r区域中最多有p个对象，因此称此对象为网格中心对象[14]，而两个多维空间之间的最佳距离为：

(10)

式中i和j为两个不同的对象，d(i,j)为两个数据之间的最佳距离，n为空间维度，xi1,xi2,...,xin与yi1,yi2,...,yin为n维空间中的数据。该算法是基于两个数据之间最佳距离来计算区域中的对象总数[15]，如果数量超过阈值p，就可以将其挑选出来，移动到密集单元集合D中，然后在集合中找出初始聚类中心，利用系数K进行聚类计算。

为了使得到的效果优于原始值[16]，将网格内的数据进行分离，运用数据之间的差异算法来进行评价，假设一组数据X={x1,x2,...,xN}，并且分成k个小组为C1,C2,...,Ck，而每一组的聚类中心分别为m1,m2,...,mk，将网格数据中的某一点与聚类中心的距离定义[17]为：

(11)

而数据间的特异性决定聚类之间的差别[18]，那么将网格数据中的边缘与聚类中心的距离定义为：

(12)

式中N为数据总数，Cj小组的聚类中心为mi，而mj为小组中的数据，d(mi,mj)为Ci与Cj之间的距离，基于以上两个距离，得到一个有效的评价函数V(k)：

(13)

由以上公式可知，只有函数的范围保证在[-1,1]之间，当函数的值趋近于1时，代表网格内数据之间的差异性越小，聚类的效果比较明显；当函数的值趋近于-1时，代表聚类方法失败，所以当Vk的值达到最大时，其系数K就为最佳聚类系数。

2.4 网格聚类

在上述处理的过程上，采用网格数据聚合计算的方法将有限的空间分割成多个小单元[19]，这些独立的小单元各自形成了一个网格结构，然后数据就会依附在网格上进行聚类，假设一个网格结构中的数据总数上限为γ，那么超过上限的网格单元就是一个密集单元[20]，超过一个以上的密集单元就可以将其定义为最大的网格单元集合。若用t代表一个聚类，将其定义为2b长的0-1串a1,…,a2b-1，其中2b代表密集单元的数量，i为其中的一个数据，当ai=1时，i则处于聚类之内，反之ai=0。文中假设数据的计量单位是“块”，那么以块X1,X2,...,Xi的方式达到网格结构，每一块都可以在本身存在的网格内进行转换，利用随机抽样的方式抽取数据，那么其目的就是完成设定的目标，数据自行聚类，结果为R1,R2,...,Rn，其中R代表每块数据X1,X2,...,Xi聚类后的结果，n代表数量。

为了保证每个聚类都不丢失其中的主要数据信息，在其进行移动时就可以随机保存多个密集单元[21]，因此所有信息都会被密集单元所携带，并将信息继续传递下去。假设在t时刻完成的数据为X1，总数为m，此时将密集单元进行定义：如果从t时刻为初始聚类，计算每一个网格单元μ中的数据密度，那么其密度满足：

den(u)>γ(t-i+1)m

(14)

式中γ为数据密度上限。单个数据的聚类思想是如以上描述的方式，而整个数据集合的数据流聚类的核心就是先容纳所有数据块X1经过，将其携带的数据都有规律的放入相应的网格结构中，然后再计算其中数据的密度，并找出密集单元；然后搜索得到最大的密集集合，在原有的聚类基础上，重新将数据流去除、新增和组合[22]。而对于重新加入的网格单元μ，将会出现三种情况：如果周围没有与之相呼应的单元，那么就要新建一个密集单元，互相结合得到新的聚类；若存在与其相对应的网格单元ω，那么就将μ融合到新的单元ω；若其对应的单元：

ω1,ω2,…,ωk(k>1)

(15)

则可以把ω1,ω2,...,ωk所在的聚类全部结合到一个网格中，而融合后的单元μ就会被取缔，这时也会出现三种情况：如果所有聚类中存在空的密集单元，那么该单元就要被取消；如果聚类中的密集单元都是有所关联的，那么就可以将单元μ去除，其他单元不变；如果聚类中的密集单元均为任何关联，那么该聚类就要分割，分别放入其他聚类中。在以上条件的约束下，重新将密集单元进行聚类。

基于上述过程，实现城市配电网多级网格数据的聚合。

3 基于隐私同态的数据加密

3.1 隐私同态加密原理

隐私同态加密原理，即对加密的数据进行处理得到一个输出，再将这一输出进行解密，其结果与用同一方法处理未加密的原始数据得到的输出结果是一样的。操作人员可以在加密的数据中进行检索、对比等操作，得到正确的结果，而在整个处理过程中无需对数据进行解密。其重要意义在于，真正从根本上解决云计算等将数据及其操作委托给第三方时的保密问题。

隐私同态加密算法简要介绍如下：

(1)加密Enc(m)：r=2^n,p=2^n^2, 计算c=m+2r+pq；

(2)解密Dec(c)：m=(cmodp) mod 2；

(3)密钥：奇数p，远远大于r、m，q远大于p。

其中，加密操作为Enc，解密操作为Dec，明文为m，mod表示模运算。明文空间是{0,1}，密文空间是整数集。p是一个正的奇数，q是一个大的正整数(没有要求是奇数，它比p要大的多)，p和q在密钥生成阶段确定，p看成是密钥。而r是加密时随机选择的一个小的整数(可以为负数)。

3.2 隐私同态技术加密聚合

通过上述过程对所有数据聚合，为保证数据的安全性，防止城市配电网多级网格数据丢失和篡改，采用隐私同态技术加密聚合后的数据，过程如下所示：

(1)建立融合树[23]，将聚合后的数据发送到离基站节点最近的某个传感器节点，将距离最近的节点记作n0，构建起以n0为中心的加密树；

(2)对同态Hash函数参数g发布，g为一个大素数；

(3)为网格内数据分配ID号[24]，在有数据查询请求后，各个传感器节点对数据检测，并将隐私数据存储到内存中；

(4)对数据加密处理，将聚合后的数据进行加密处理，加密算法表示为：

Ci=Enc(mi)=mi+IDi

(16)

式中mi为隐私数据；IDi为第i个数据的ID号；Enc为数据加密参数：

(5)对同态消息验证码计算[25]，在隐私同态技术中，各个传感器能够计算出感知数据的同态消息验证码;

(6)将密文信息和聚合数据的消息验证码上传到融合节点中，构建基于隐私同态的数据聚合加密模型，从而实现城市配电网多级网格数据的聚合，其表达式为：

H(mi)=gmi

(17)

4 仿真实验对比

为验证所提出的城市配电网多级网格数据聚合算法的有效性，采用Matlab软件搭建城市配电网多级网格数据模型仿真平台并在此平台下进行实验分析。实验数据取自某城市电网公司建立的配电网多级网格数据库，该数据库含有2 000个数据，对数据进行分组，数据集的元组数设为10，配电网多级网格数据设置情况如表1所示。

表1 配电网多级网格数据设置情况

根据密度阈值函数设置对配电网多级网格数据进行预处理，并将文献[1]提出的基于雾计算的聚合方法与文献[2]提出的基于雾辅助的方法与所研究方法对比，对比三种方法的聚合效果。

4.1 数据丢失情况对比

图3为三种方法在数据聚合后，数据丢失的对比结果。

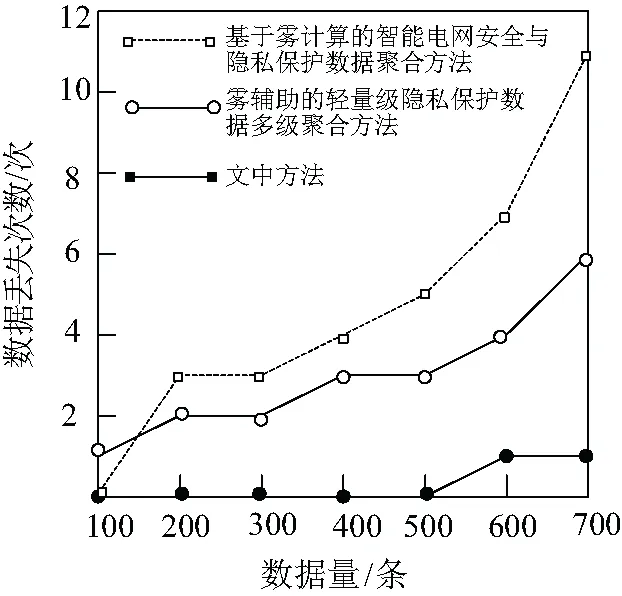
图3 数据丢失情况对比

基于图3可知，文中方法在数据量为100条到500条时没有出现数据丢失情况，在数据量增多到1 000条时出现了数据丢失情况，但是丢失数量在1次内，丢失数量较少，在可接受范围内。而基于雾计算的聚合方法与雾辅助方法数据丢失情况较多，聚合效果较差。主要是因为文中方法采用隐私同态技术加密聚合后的数据，保证了数据的安全性，最大限度防止了城市配电网多级网格数据丢失，由此可以证明文中方法在数据聚合过程中能够保证数据的防丢失安全性。

4.2 数据篡改情况对比

对比经过三种方法聚合后数据被篡改的情况，结果如图4所示。

图4 数据篡改情况

由图4可知，文中方法的数据篡改次数在2次内，出现的被篡改情况较少，而其他两种方法均发生不同情况的数据篡改情况，主要是因为文中方法采用隐私同态技术加密聚合后的数据，保证了数据的安全性，最大限度防止了城市配电网多级网格数据被篡改。由此可以证明文中方法在数据聚合过程中能够保证数据的防篡改安全性。

4.3 数据聚合效率对比

在数据聚合中，仅仅关注数据的完整性和机密性是远远不够的，信息聚合的时效性也非常重要，为此对比三种方法的数据聚合效率，对比结果如图5所示。由图5可知，所研究的城市配电网多级网格数据聚合方法聚合效率最高，在数据多与少的情况下，所花费的数据聚合时间都较少。而基于雾计算的聚合方法，以及雾辅助的聚合方法受到数据量影响较大，在数据量较多时，花费的聚合时间较多。而文中在密集单元里选出一个位移最大的初始值作为聚类中心，将噪声的干扰降到最低，从而提升了算法的运行效率。

图5 数据聚合效率对比

4.4 数据加密效率对比

三种方法的数据加密效率对比结果如图6所示。由图6可知，其他两种方法的数据加密时间较多，文中方法研究的数据加密时间远远少于这两种方法。主要原因是文中方法采用了隐私同态方法对数据加密，隐私同态技术不需要对数据密钥分配，简化了加密流程，从而减少了数据加密的时间。

图6 数据加密效率对比

4.5 通信开销对比

对比三种方法在传输数据时产生的通信开销，对比结果如图7所所示。由图7可知，文中方法通信开销维持在同一量级，通信开销较低，且远低于其他两种方法的通信开销，说明所研究的方法不仅能够减少数据聚合时间，还能够减少数据通信开销。主要原因是文中方法将数据的格式转化成与大多数数据相同的格式，重新获取新的数据，保证了数据获取的完整性，降低了数据通信开销。

图7 通信开销对比

5 结束语

文中提出了基于隐私同态的城市配电网多级网格数据聚合算法。(1)预先对数据采样，保证数据聚合的完整性；(2)提出网格聚类算法，对聚类中心与密度函数选择，保证数据的准确聚类；(3)将隐私同态技术应用到数据聚合中，在保证数据顺利聚合的同时，保证数据的安全性。

实验算例表明，通过对比已有经典聚合方法，文中所提出的基于隐私同态的城市配电网多级网格数据聚合算法，数据丢失数量限制在1次内，数据篡改次数限制在2次内，减少聚合后数据丢失与被篡改的次数，还能有效提高数据加密效率与聚合效率，并显著降低数据的通信费用。