带隔板底水油藏直井临界产量及其极值研究
朱圣举 朱 洁 王思仪 马维云
(1. 中国石油长庆油田分公司 勘探开发研究院, 西安 710018;2. 低渗透油气田勘探开发国家工程实验室, 西安 710018;3. 中国石油长庆油田分公司 第六采气厂, 西安 710018;4. 中国石油长庆油田分公司 第八采油厂, 西安 710021)
0 前 言
在带隔板底水油藏直井开发中,假设隔板上部油层全部射开、下部油层不射孔,则从油井开始生产时原始油水界面逐渐呈圆台形上升而形成底水锥进。随着油井产油量的增加,水锥高度逐渐上升,直到产油量达到某一个定值时水锥突破,油井见水,此时的最大无水产油量即带隔板底水油藏直井的临界产量。
Guo等人研究了无隔板底水油藏直井临界产量公式(以下称“Guo氏公式”),并求得了最佳射孔程度[1]。此后,一些学者在Guo氏公式的基础上作了深入研究。张兴国等人研究了夹层对底水的抑制作用[2-3]。李春兰等人进一步研究了带气顶底水油藏直井的最佳射孔位置及程度,但未对Guo氏公式作修正[4]。朱圣举等人研究了带隔板底水油藏直井的见水时间,但并未涉及临界产量[5-7],之后又重新修正了Guo氏公式[8]。李传亮等人推导出了带隔板底水油藏直井的临界产量公式,计算结果显示当油层射开厚度为零时的临界产量最大,这显然不符合实际情况[9-11]。何巍等人进一步对带隔板的油井临界产量公式作了改进,考虑了油层射孔程度的影响,但并未对Guo氏公式进行修正[12-14]。
在这些后续研究中,仍未能统一认识或推导出合理的带隔板底水油藏直井临界产量公式,也未就最佳隔板位置作深入讨论。因此,本次研究将依据渗流力学理论,重新推导带隔板底水油藏直井的临界产量公式。
1 带隔板底水油藏直井数学模型的建立
1.1 扇状曲面面积公式
假设油藏属性为均质且各向同性,忽略毛管力及表皮因子,以稳定渗流为主(见图1)。以半径为ξ的曲线弧绕z轴旋转一周形成扇状曲面,其面积公式如式(1)所示[15]:

图1 带隔板底水油藏直井渗流示意图

(1)
式中:A—— 扇状曲面面积,m2;
r—— 垂直于z轴的xOy平面上的极坐标,m;
rb—— 隔板半径,m;
ξ—— 扇状径向渗流半径,m;
b—— 半径上限,m;
φ0—— 线段CD、CE的夹角, (°)。
此扇状体曲面上的任一点,存在式(2)所示关系:
z2+(r-rb)2=ξ2,rb≤r≤rb+ξ
(2)
式中:z—— 自A点垂直向下的z轴坐标值,m。
变换式(2),得到式(3):
(3)
于是有式(4):
(4)
将式(4)代入式(1),得到式(5):

(5)
求解积分之后,得到式(6):
(6)
当b→rb+ξ时,得到式(7):
A=2πξ2cosφ0+π2rbξ-2πrbξφ0
(7)
经过推导,将扇状曲面的面积A转换成ξ的函数,且扇状曲面垂直于ξ。
1.2 扇状径向渗流流量公式
据达西渗流定律[16],推导得到式(8)所示扇状径向渗流流量公式:
(8)
式中:Qs—— 扇状径向渗流流量,m3/d;
C1—— 常数,取0.086 4;
K—— 储层渗透率,10-3μm2;
μ—— 流体黏度,mPa·s;
re—— 油井的泄油半径,m;
rwb—— 隔板边缘水锥顶点处的渗流半径,m;
pe——re处对应的压力,MPa;
pb—— 隔板边缘rb处的压力,MPa。
将式(7)代入式(8),推导得到式(9):
(9)
令π-2φ0=θ0,θ0为定义角。对式(9)求积分,得到式(10):
(10)
由于
(11)
式中:H—— 总油层厚度,m;
h—— 隔板以上的油层厚度(全部射开),m。
将式(11)代入式(10),得到式(12):
(12)
1.3 带隔板底水油藏直井临界产量公式
首先,计算上部平面径向渗流的流量,如式(13)所示:
(13)
式中:Qr—— 上部平面径向渗流流量,m3/d。
然后,得到上部平面径向渗流任一点的压力分布公式,如式(14)所示:
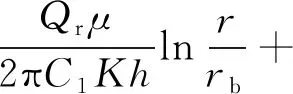
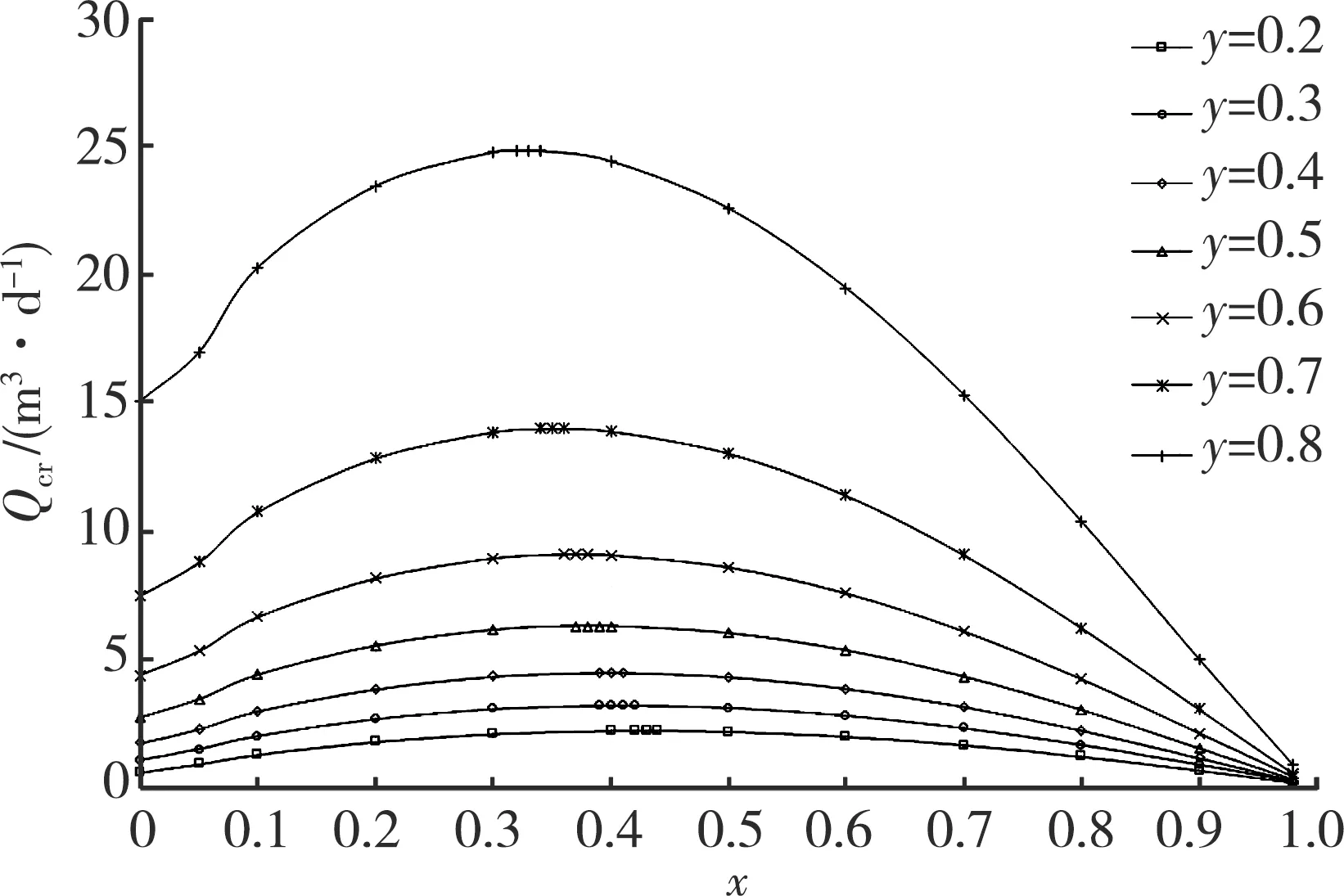
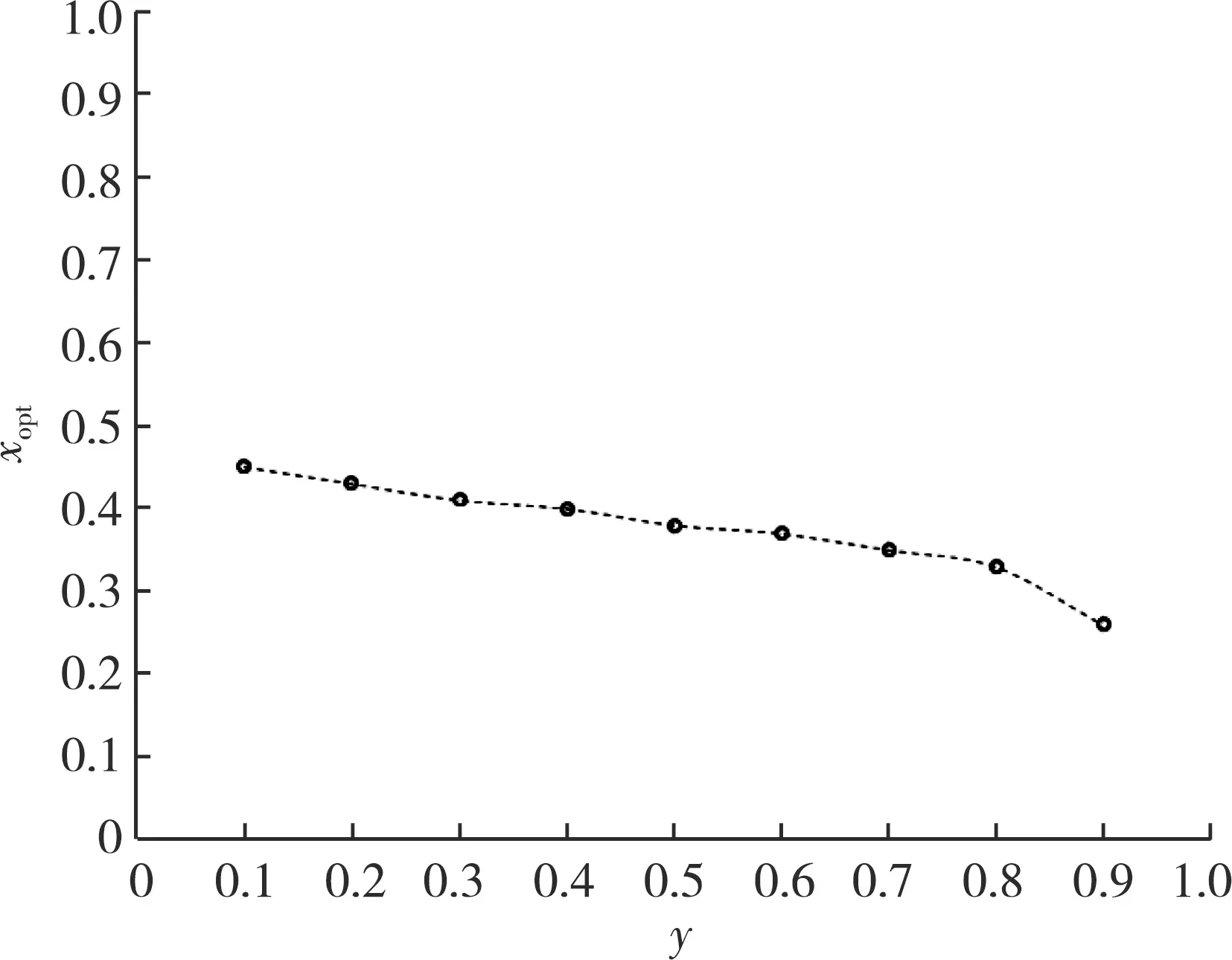
pb0+C2γoz, 0 (14) 式中:p(r,z) —— 上部平面径向渗流任一点压力,MPa; C2—— 常数,取0.001; γo—— 原油的容重, kN/m3; pb0——rb处油层顶部的压力,MPa。 由式(12)得到下部扇状径向渗流任一点的压力分布公式,如式(15)所示: pb0+C2γoz,h (15) 式中:p(ξ,z) —— 下部扇状径向渗流任一点压力,MPa。 在两种流动模式的分界面上,即在界面z=h及ξ=r-rb上,式(14)与式(15)的压力应当相等。因此,在界面z=h及ξ=r-rb=re-rb构成的圆弧上,Qr与Qs的关系如式(16)所示: (16) 则可得到产液总量公式,如式(17)所示: (17) 式中:Qt—— 全井产液总量,m3/d。 接着,讨论水锥顶点(rb)处的情况。当位于顶点油侧时,由式(15)可得式(18): pb0+C2γo(h+ξz) (18) 式中:po(ξz) —— 水锥顶点油侧的压力,MPa; ξz—— 下部扇状径向渗流模式中从隔板边缘垂直向下的距离,m。 水锥顶点静水压力的计算,如式(19)所示: pw(ξz)=pe0+C2γoH-C2γw(H-h-ξz)(19) 式中:pw(ξz) —— 水锥顶点的静水压力,MPa; γw—— 水的容重,kN/m3; pe0——re处油层顶部的压力,MPa。 此时,设: f(ξz)=pw(ξz)-po(ξz) (20) 如果要使最大的水锥保持稳定,则必须在水锥顶点满足以下条件: 条件Ⅰpw(ξz)=po(ξz),其函数如式(21)所示: f(ξz)=0 (21) 条件Ⅱ油相的垂向压力梯度必须等于静水压力梯度,其函数如式(22)所示: (22) 将式(18)和式(19)代入式(20),则得到式(23): (pe0-pb0)-C2Δγ(H-h-ξz) (23) 其中Δγ=γw-γo。再由式(15),得到式(24): (24) 将式(23)和式(24)代入式(21),得到式(25): C2Δγ(H-h-ξz)=0 (25) 将式(25)代入式(22),得到式(26): (26) 变换式(26)后,得到式(27): (27) 将式(27)代入式(25),令C=C1·C2= 86.4×10-6,得到扇状径向渗流临界产量方程,如式(28)所示: (28) 式中:x—— 隔板位置系数,x=h/H; y—— 隔板封隔系数,y=rb/re。 通过式(28)无法直接求得扇状径向渗流流量(Qs)的临界产量解析解,因此,改用数值法进行求解。将求解得到的Qs代入式(17),即可得到全井的临界产量(Qcr)。 临界产量公式的适用条件如式(29)所示: (29) 以鄂尔多斯盆地某砂岩底水油藏YZQ为实例,运用推导出的公式进行分析。该油藏采用直井开采方式,主要参数为:H=15 m;K=142×10-3μm2;μ=2.0 mPa·s;Δγ=1.47 kN/m3;rw=0.1 m;rwb≈0.1 m;re=250 m。 为了研究临界产量与隔板位置的关系,分别取不同的x、y值,将该油藏开发初期的实际数据代入式(17)和式(28)。经过计算发现:在同一隔板封隔系数下,随着隔板位置系数的逐渐增大,临界产量呈先增大后减小的变化趋势,且其间存在一个极大值;在同一隔板位置系数下,随着隔板封隔系数的增大,临界产量呈逐渐增大的变化趋势。在不同隔板封隔系数下,临界产量与隔板位置系数的关系如图2所示。 图2 不同隔板封隔系数下临界产量与隔板位置系数的关系 (1) 以Z1井、Z2井、Z3井为例。其隔板位置系数分别为0.30、0.40、 0.60;泥岩隔板厚度均为1.0 m,隔板封隔系数均为0.40 。将实际参数代入式(17)和式(28)进行计算,求得Z1井、Z2井、Z3井的临界产量分别为4.36、4.51、3.89 m3/d。这3口井开发初期的实际产液量均为4.50 m3/d,其中Z2井经过6个月的生产期才见水,而Z1井、Z3井分别只经过了3个月、2个月的生产期即迅速见水。相比之下,Z1井、Z3井的实际产液量均超过了其临界产量,而Z2井的实际产液量未超过其临界产量,无水采油期相对较长。 (2) 以Z4井、Z5井为例。其隔板封隔系数分别为0.40、0.50;泥岩隔板厚度均为0.8m;隔板位置系数均为0.50。将实际参数代入式(17)和式(28)进行计算,求得Z4井、Z5井的临界产量分别为4.35、6.03 m3/d。这2口井开发初期的实际产液量均为5.50 m3/d,Z5井经过8个月的生产期才见水,而Z4井只经过了3.5个月的生产期即迅速见水。相比之下,Z4井的实际产液量超过了其临界产量,而Z5井的实际产液量未超过其临界产量,无水采油期相对较长。 为了分析最佳隔板位置系数 (xopt)的分布区间,绘制了最佳隔板位置系数与隔板封隔系数的关系曲线(见图3)。分析结果表明:随着隔板封隔系数的增大,最佳隔板位置系数呈逐渐减小的变化趋势;而且,当隔板封隔系数为0.2~0.8时,最佳隔板位置系数主要分布于0.33~0.43,相对比较集中。此分析结果可为实际生产过程中的打隔板作业提供参考[17]。 图3 最佳隔板位置系数与隔板封隔系数的关系 本次研究中,基于渗流力学理论重新推导了带隔板底水油藏直井临界产量公式。通过这次公式推导,对射孔厚度为零时临界产量最大这一问题作了修正,并明确了隔板位置系数最佳值的计算。最后,运用新公式针对带隔板底水油藏进行了实例分析。结果表明: 在同一隔板封隔系数下,随着隔板位置系数的逐渐增大,临界产量呈先增大后减小的变化趋势,且其间存在一个极大值;在同一隔板位置系数下,随着隔板封隔系数的增大,临界产量呈逐渐增大的变化趋势。同时,随着隔板封隔系数的增大,最佳隔板位置系数呈逐渐减小的变化趋势;当隔板封隔系数为0.2~0.8时,最佳隔板位置系数主要分布于0.33~0.43,相对比较集中。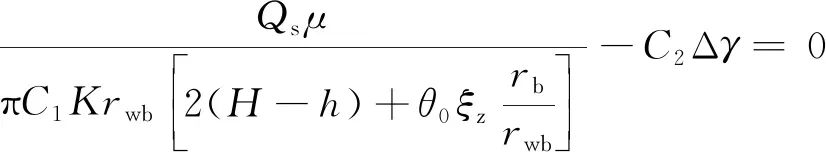
2 实例分析
3 结 语

