基于改进遗传算法的异步并行拆卸序列规划

孙娴静，唐秋华，邓明星

(武汉科技大学 1.冶金装备及其控制教育部重点实验室；2.机械传动与制造工程湖北省重点实验室；3.汽车与交通工程学院，湖北 武汉 430081)

拆卸是将产品或装配体进行拆解，获取目标零部件的过程。与焚烧、掩埋等其他报废产品处理方法相比，通过拆卸来获取可直接重用或可修复的零部件，实现资源的再利用，故而拆卸具有显著的经济和环境优势，在报废产品的再利用和再制造过程中具有重要的地位。

拆卸序列规划是指根据产品中零部件之间的几何结构、功能等一些预定的性能指标探索确定合理可行的拆卸序列，并从中选择最优的序列以指导产品的拆卸，达到预期的拆卸目标。根据拆除零部件的逻辑顺序，拆卸可以分为两大类：顺序拆卸和并行拆卸。因此，拆卸序列规划也可以分为顺序拆卸规划和并行拆卸规划。并行拆卸分为同步并行拆卸和异步并行拆卸。

到目前为止，已经有很多学者对顺序拆卸规划问题进行了研究，开发出许多模型和方法。但随着技术的发展，对拆卸时效的要求逐渐提高，并行拆卸序列规划问题越来越受到学者的关注与研究。Zhang等[1]针对性地建立拆卸混合图模型来解释4种不同的零部件之间的结构连接，然后提出协同拆卸层次树的生成方法，通过一种基于两用户定义变量的分支定界算法计算出并行拆卸序列规划的最小工作时间。随后，Zhang等[2]基于模糊粗糙集，定义和推导了装配约束因子、拆卸优先因子、拆卸时间因子、拆卸工具因子和组合类型因子等5个拆卸因子，建立了并行拆卸的模糊−粗糙集映射模型，利用模糊−粗糙集映射模型生成最优的并行拆卸序列。Smith等[3]利用模块化设计理论将待拆卸的零件转化为模块，并根据递归规则生成可行的拆卸序列，然后利用遗传算法寻找最优的并行拆卸序列。Ren等[4]创建拆卸层次树形图来描述并行拆卸过程，并提出一种多目标离散人工蜂群算法，使求得的并行拆卸序列规划的拆卸时间最小化，利润最大化。

然而，以上文献主要针对同步并行拆卸序列规划，要求操作者同时开始拆卸操作，从而导致空闲时间多，作业效率低。因此，本文针对异步并行拆卸序列规划问题，提出改进遗传算法进行求解。

1 异步并行拆卸序列规划

异步并行拆卸是并行拆卸方式中的一种。异步并行拆卸是指允许操作者完成当前拆卸任务后，在不违背相关约束的情况下即时开始下一个拆卸任务，不必等待所有操作者都完成任务[5]。在并行拆卸序列规划中，操作者开始执行拆卸操作的时间也尤为重要，会对产品拆卸的完成时间以及拆卸成本产生不小的影响。异步并行拆卸节省了部分操作者等待其他拆卸任务完成的空闲时间，减少了完成拆卸所需要的时间以及相关成本，更具有研究价值。

1.1 优先关系约束

优先关系表示产品零部件之间的拆卸先后顺序，根据逻辑关系对其进行划分，可以分为“与优先”关系和“或优先”关系。“与优先”关系指只有拆除所有紧前优先零部件，零件i才能被拆除。若同时有多个零部件对零件i具有优先关系，拆除其中某一个零部件，零件i即可拆卸，则零件i与其紧前优先零部件构成“或优先”关系[6-7]。

图1为某产品的优先关系示意图。其中，i={1,2,···,10}表示待拆卸任务，每个拆卸任务表示要拆卸的零部件，其优先关系由优先级高的零件指向优先级低的零件。在图中，用有向点虚线边连接的任务2、3与任务1、8、9、10之间构成 “或优先”关系。若零部件2被拆卸，零部件1、3、8、9、10均可被拆卸。其余有向实边接连的拆卸任务接触约束关系为“与优先”关系。

图1 某待拆卸产品的优先关系示意图Figure 1 Schematic diagram of the priority relationship of a product to be disassembled

通常，在某一拆卸方向上的各零部件之间的优先约束关系总是严格对接的，当出现“或优先”关系则说明要想拆卸某一产品，至少有2种不同的拆卸方式，即至少有2种不同的拆卸方向。因此，在含有“或优先”关系的情况下，可以不用考虑产品的拆卸方向，在一定程度上简化了问题。

1.2 工作区域冲突约束

在异步并行拆卸序列规划中，通常是多个操作者共同拆卸一个产品，由于各零部件间存在复杂的装配关系，会存在当某个操作者拆卸某一零件时会占用另一个操作者的拆卸工作区域，使得另一个操作者的拆卸工作无法进行的问题。这时，2个操作者无法同时完成各自的拆卸任务，这种情况称为2个零部件之间存在工作区域冲突关系。

为了方便表达，可以像优先关系矩阵一样构造一个冲突矩阵C来描述。

2 加入路径重连的改进遗传算法

2.1 编码

由于异步并行拆卸序列规划问题不仅涉及到每个任务之间的约束关系，与操作者也相关，因此采用双向量列表结构编码更加合适，个体v由拆卸任务向量v1和 操作者向量v2组成。拆卸任务向量v1={i1,i2,···,ik}，向量中每个元素代表一个待拆卸任务，由1到K的整数表示，K为待拆卸产品的零部件总数。操作者向量v2={r1,r2,···,rN}，向量中每个元素代表执行向量v1中对应的拆卸任务的操作者，由1到N的整数表示，N为操作者数量。

在确定遗传算法的编码方式之后，需要根据问题特点生成初始化种群，以本文1.1节中提出的问题为例进行说明。拆卸任务向量v1只与待拆卸产品的各零部件有关。为方便解码，需要在种群初始化时保证向量v1的可行性，即严格遵循各零件之间的优先关系约束。由优先关系矩阵可知，当优先关系矩阵P中 第j列中的元素均为0时，待拆卸任务j当前可拆卸，不受其余零件的优先约束。将得到的可拆卸任务依次存入向量v1，不断循环直至找出所有拆卸任务，此时可得到拆卸任务向量v1，操作者向量v2可以由操作者数量通过随机程序获得。初始化种群具体步骤如下。

步骤 1输入优先关系矩阵P，创建空向量v1和空集合t1。

步骤 2若矩阵P为空矩阵，则转到Step7，否则执行Step 3。

步骤 3找出矩阵P中 元素全为0的列，将列对应的拆卸任务存入集合t1中。

步骤 4从集合t1中随机选择一个待拆卸任务放入到向量v1最左端中。

步骤 5更新矩阵P，将已拆卸任务的行与列删除，若删除的元素中包含“或优先”关系，则同时对与之关联的其他“或优先”关系元素进行修改。

步骤 6将集合t1中已拆卸任务删除，返回Step 2。

步骤 7根据操作者数量随机生成向量v2。

步骤 8输出向量v1和 向量v2。

2.2 解码

在本文研究的异步并行拆卸序列规划问题中，拆卸的目标为拆卸完成时间最小，即最小化最大拆卸完成时间，类似于JSP问题的最大完工时间。与JSP问题不同，在异步并行拆卸序列规划问题中还要考虑“与/或优先”关系和操作者的拆卸工作区域冲突问题。 “或优先”关系存在不定向性，在未开始拆卸之前，多个具有“或优先”关系的待拆卸任务具有同样的拆卸优先级，无法选择哪个任务先进行拆卸。

因此，在解码开始之前，要将拆卸任务之间的“或优先”关系解除。仍以1.1节中的问题为例，通过编码，该产品所有拆卸任务的拆卸顺序已经出来，可以修改优先关系矩阵P，解除拆卸任务之间的“或优先”关系。 假设个体编码v1={3,9,2,10,8,4,7,1,5,6}，则可以看作拆卸任务3对任务1、8、9、10具有“与优先”关系约束，任务2不再对后续任务具有“或优先”关系约束。对应的，优先关系矩阵可以修改为P21，P28，P29，P2,10为 0；P31，P38，P39，P3,10为1，其余保持不变。

解码是根据种群个体编码计算出每个个体对应拆卸序列的最大完成时间。首先，创建存放所有待拆卸任务开始拆卸时间的矩阵 st和所有待拆卸零件结束时间的矩阵 ft 。 按照编码v1的顺序对每个待拆卸零件进行拆卸，将拆卸开始时间存入矩阵 st中对应的位置，拆卸结束时间存入矩阵 ft中对应的位置。当遇到某一具有前序拆卸任务的拆卸任务时，比较其前序任务的结束时间，与所在并行序列的上一个任务结束时间，取较大值为该任务的开始时间。当计算完时间后，还需要判断当前任务是否存在工作区域冲突，若存在，则对该个体进行惩罚，若不存在则继续计算下一个任务。

判断零部件之间是否存在工作区域冲突主要有3个判断标准：1) 两任务之间是否还存在优先关系；2) 两任务中某一任务是否还有前序任务未执行；3) 两个任务的执行时间是否重叠。若2个具有工作区域冲突关系的拆卸任务同时不满足以上3个条件，则它们之间会产生工作区域冲突，该解为不可行解。

2.3 遗传算子设计

遗传算法中的选择操作是对种群进行选择，从而使优秀基因遗传到下一代。本文采用轮盘赌选择方法。

遗传算法中的交叉操作是对种群中被选择的两个个体的编码片段进行部分交叉，从而产生两个新个体的过程。本文对向量v1采用优先保存交叉(precedence preservation crossover, PPX)方法[8-9](图2)。PPX可以将父代的优先关系传递给新的子代，从而保证子代的可行性；对向量v2采用单点交叉方法，在向量的长度范围内随机选择一个交叉点，将两个个体的向量v2从交叉点初断开，并互换前半部分，即可获得两个新的子代v2。

图2 PPX操作示意图Figure 2 Schematic diagram of PPX operation

遗传算法中的变异操作是以一定概率使个体中的基因发生变异以产生新个体的过程。若在向量v1上进行变异操作，可能会产生不符合优先关系约束的不可行解。本文选择基于向量v2进行一个简单突变：从向量v2中随机选择一个变异点，将其值更换为其他并行序列。

2.4 路径重连算子设计

路径重连通过使用在搜索过程中得到的一组不同的高质量解对启发式算法实现进一步收敛和优化。在每个迭代中，路径重连应用于全局搜索阶段结束时找到的解决方案和从精英集中随机选择的解决方案，返回与这两个解决方案相似但可能更好的新解决方案[10]。

2.4.1 路径距离计算

在算法开始前，定义以下参数[11]。MoS为个体S中分配给拆卸任务o的操作者；LSM为个体S中分配给操作者的拆卸任务数；为o在操作者MoS上的位置。若两个个体中的拆卸任务o被分配给同一个操作者进行拆卸，则定义两个个体之间o的距离为

若两个个体中的拆卸任务o被分配给不同的操作者进行拆卸，定义两个个体之间o的距离为

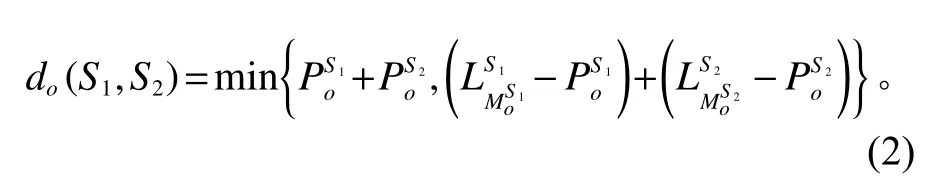
个体S1和S2之间的距离定义为

2.4.2 重连策略

在遗传算法每次迭代完成后，选取出最优的部分个体组成精英集，并随机选择出两个个体，一个作为初始解Si，一个作为引导解Sg进行路径重连。设Sc为 当前解决方案(Sc初 始化为Si)。

首先，构造路径重连过程中得到的解集N：对于Sc中 的每个拆卸任务oi依 次进行判断，若oi在解Sc和 解Sg中分别位于不同操作者上，将Sc中的oi移动到Sg中的操作者上(位置不变)。比较移动前后解Sc和Sg中oi的距离，选择其中较短的存放入解集N中；若oi在 解Sc和 解Sg中同一操作者的不同位置上，改变解Sc中oi的位置，并将改变后的解存入解集N中。然后，删除解集N中的不可行解，以及到Sg的路径距离大于初始路径距离(解Sc到Sg的距离)的解，计算剩余解的拆卸完成时间。然后，对于N中剩下的解S，按拆卸完成时间大小进行升序排列，从中选择拆卸完成时间最小的解作为路径上的下一个Sc。若该解的最小完成时间优于初始解的拆卸完成时间,则同时将其存储在优解集合Path中。重复以上步骤直到无法再得到更优的解。最后，返回优解集合Path中完工时间最短的解Sr。

3 实验分析

3.1 案例说明

在1.1节的案例中，令操作者(并行序列)的数量为2，运行程序，结果如图3所示。

图3 程序运行结果Figure 3 Results on program running

图3中的柱形表示每个操作者进行操作的拆卸任务，各个任务从甘特图最左边开始依次被操作者进行拆卸，柱形上的数字对应的是正在拆卸的任务的序号。

从图3中可以发现，各操作者在零件拆卸过程中无空闲时间，最大化利用了资源，证明本文所述程序有效。

3.2 路径重连性能分析

3.2.1 参数校验

使用田口实验对精英解个数、种群大小、交叉概率、变异概率等参数进行校验，结果如图4所示(信噪：望小)。信噪比是质量影响因子的主效应与误差效应的比值。一般地，信噪比值越大，其稳健性越好。由图4可知，最佳参数组合：精英解个数为10，种群规模为100，交叉概率为0.7，变异概率为0.2。

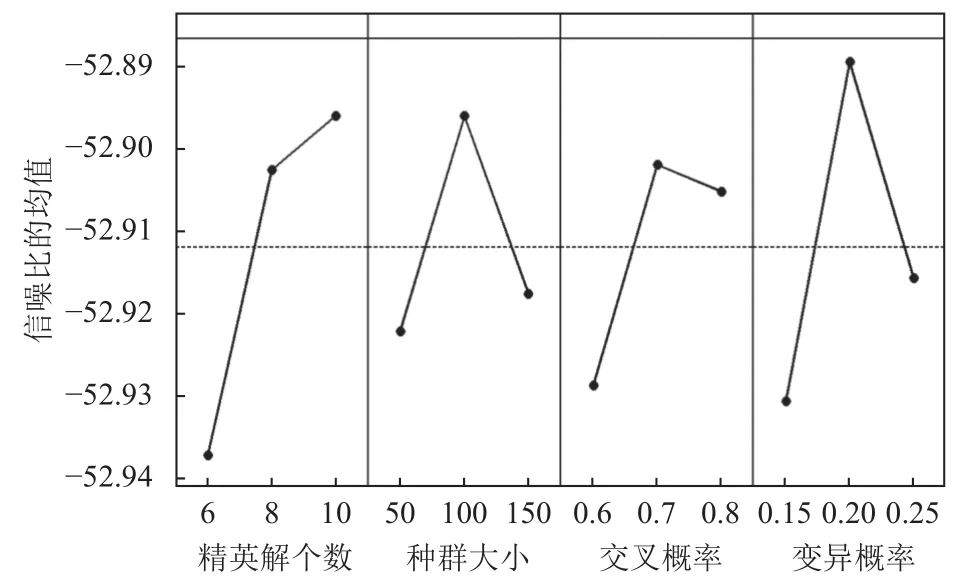
图4 平均完成时间的信噪比−主效应图Figure 4 S/N ratio of average completion time-main effect diagram

3.2.2 路径重连有效性

为验证所提路径重连策略的性能，令多个实际拆卸案例[12-14]采用最佳参数组合进行运算。为了对多种路径重连方法进行区分，将采用精英解与精英解之间进行路径重连的方法称为 G A−PR1，劣解向精英解进行路径重连的方法称为 G A−PR2。 固定上述算法的CPU运行时间t为N×N×0.01 s，每个案例的3种算法均运行10次。表1展示了相同运行时间下各算法的相对分析误差(RPD)。

由表1可知，GA-PR1在最小RPD和平均RPD方面的表现均优于GA和GA-PR2。此外，绘出3种算法在95%置信区间下的区间图，如图5所示。结合图表可得，在相同的CPU运行时间内，GA-PR1运行得到的结果更好且更加稳定。

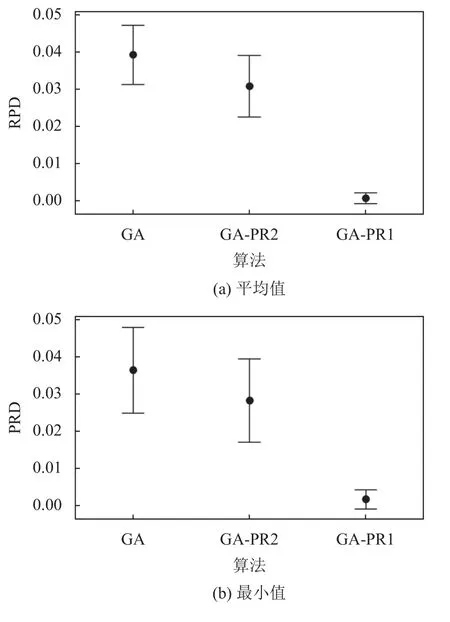
图5 3种算法(GA、GA-PR2和GA-PR1)在95%置信区间下的区间图Figure 5 Interval graphs of the three algorithms (GA, GA-PR2 and GA-PR1) under the 95% confidence interval

表1 GA、GA-PR2和GA-PR1的相对分析误差Table 1 RPD of GA、GA-PR2 and GA-PR1

3.3 算法性能分析

为分析所提算法的综合性能，将算法GA-PR1与参考文献[6]中提出的改进遗传算法IGA及改进离散蜜蜂算法MDBA[15]进行对比实验。

通过田口实验确定各算法的最佳参数组合(表2)，对21个案例在相同的CPU运行时间分别运行10次，结果如表3所示。根据表3绘制出3种算法在95%置信区间下的区间图，如图6所示。

表2 各算法参数校验结果Table 2 Verification results of various algorithm parameters

表3 IGA、MDBA和GA-PR1的相对分析误差Table 3 RPD of the IGA、MDBA and GA-PR1

图6 3种算法(IGA、MDBA和GA-PR1)在95%置信区间下的区间图Figure 6 Interval graphs of the three algorithms (IGA, MDBA and GAPR1) under the 95% confidence interval

从表3中可知，在平均值方面，相较于IGA，GAPR1获得了20个较优解；相较于 MDBA，GA-PR1获得了18个较优解。在最小值方面，相较于IGA，GAPR1获得了17个较优解；相较于 MDBA，GA-PR1获得了15个较优解。结合表3和图6可得，对比IGA和MDBA，所提出的GA-PR1具有更好的综合性能。

4 结论

本文采用加入路径重连的遗传算法来解决异步并行拆卸序列规划问题，并通过Matlab编程进行实现。所提出的方法具有以下特点。1) 在模型中采用“或优先”关系来判断拆卸方向，对问题进行简化。2) 采用路径重连策略，并通过实验证明其有效性。

虽然本文提出的方法已经通过案例进行验证，但在实际应用中依然存在些许不足。在实际拆卸中，往往不仅关注拆卸完成时间，更要对拆卸成本，资源消耗，拆卸利润等其他因素进行多方面权衡，寻找最佳方案，但本文所述方法仅考虑拆卸完成时间，略有不足。在以后的研究中，考虑更贴合实际的具体需求，提出更好的方法解决异步并行拆卸序列规划问题。