售前服务影响下的产品服务供应链优化研究

任晓辉，沈 瑾，苌道方

(1.上海海事大学 物流科学与工程研究院，上海 201306；2.上海电机学院 商学院，上海 201306)

近年来，客户对产品相关服务的要求越来越高。许多制造企业已经意识到，相较于单独提供产品，提供产品服务系统(product service system，PSS)可以获得更高的利润[1]。相应地，供应链模式也正在从产品供应链或服务供应链转变为产品服务供应链(product service supply chain，PSSC)，从而为客户提供产品和服务的集成[2]。在PSSC中，由产品供应商提供产品，服务集成商可以自由选择相关服务来匹配基础产品[3]，从而为客户提供定制的PSS。并且，服务集成商作为核心企业，系统地控制产品流、服务流、信息流、资金流和价值流，实现客户参与以及所有成员企业(如产品供应商、分销商等)的协同合作[4]。

对于某些高价值或技术密集型产品(例如成套设备)，客户普遍要求服务集成商为有潜在需求的产品提供售前服务。提高服务集成商的服务水平会增加企业服务成本，降低利润，但也会增加客户对于产品的需求，进而增加PSS购买量，在增加产品供应商收入的同时也增加了服务集成商的服务收入。高服务水平必然带来高服务定价，进而影响PSS购买量，影响服务集成商收入，也影响了产品的购买量，影响产品供应商收入。可见，售前服务水平和服务价格的选择直接影响着服务集成商及产品供应商的利润。此外，一个组织业务的改变将影响其他组织在供应链中的业务活动[5]。售前服务影响下的市场需求变化将引起一系列的连锁反应(如PSSC库存成本和分销成本的变化等)，对PSSC的稳定性产生影响，进而影响产品供应商的利润。因此，选择合理的服务水平和服务价格使得PSSC中的服务集成商和产品供应商在为客户提供优质服务的同时实现利润全局最优是一个值得研究的问题。

1 文献综述

近年来，有关PSSC的研究逐年增加。Johnson等[6]通过大量案例分析企业在实施面向服务的战略中所面临的机遇和挑战，并总结了PSSC和传统供应链的不同特征。Xu等[7]结合相关案例研究提出PSSC结构框架，并从价值协同生产、功能流程管理等方面阐述了该架构。上述文献从定性的角度研究产品和服务在PSSC中的整合以及供应链效率的提高。也有一些文献通过建立数理模型研究PSSC。Dan等[8]针对一个制造商和一个销售服务集成商组成的PSSC，在产品销售影响服务需求的情况下，构建制造商和销售服务集成商的利润函数。Wang等[9]研究当两个企业在产品和不同的服务捆绑销售时，如何选择最佳的服务期限、产品价格及服务水平。Xie等[10]研究PSSC环境中服务成本信息不对称的情况下，如何有效地为客户提供PSS，分析和比较批发价格合同和零售价格维持合同等合同契约，发现供应链的权利结构和成本信息类型在很大程度上决定了这几种合同的成效。这些文献主要从PSSC中某一决策者的角度进行研究，并没有考虑PSSC整体的变动。综上所述，现有文献较少有研究售前服务对PSSC的影响，且主要针对PSSC中的决策者，并不涉及PSSC成员之间的合作与协调。

鉴于此，本文针对考虑售前服务影响的PSSC，旨在从全局分析在市场需求变化的情况下PSSC各阶段的变化，选择最优的服务水平和服务价格以实现产品供应商与服务集成商的利润最优。首先建立售前服务影响下客户产品需求的效用模型，分析PSSC各阶段成本变动，构建售前服务影响下的PSSC网络优化模型。然后提出一种具有约束推理的双层嵌套遗传算法。最后通过计算某生产船舶细水雾喷淋系统建材公司的PSSC案例，并与嵌套遗传算法进行对比，验证了该算法的可行性与实用性。

2 问题描述

本文研究的是销售高技术或成套复杂设备的多级PSSC网络。此PSSC由1家产品供应商、1家服务集成商、Q个区域仓库、F个服务仓库及其覆盖范围内的A个客户构成，令={1,2,···,Q}表示所有区域仓库的集合，={1,2,···,F}表示所有服务仓库的集合，={1,2,···,A}表示客户节点的集合。产品供应商生产产品的单位成本为c，销售价格为Pp。服务集成商以价格Ps向客户提供服务水平为S的售前服务，如图1所示。各节点功能简述如表1所示。所有仓库及其供应能力均已知。

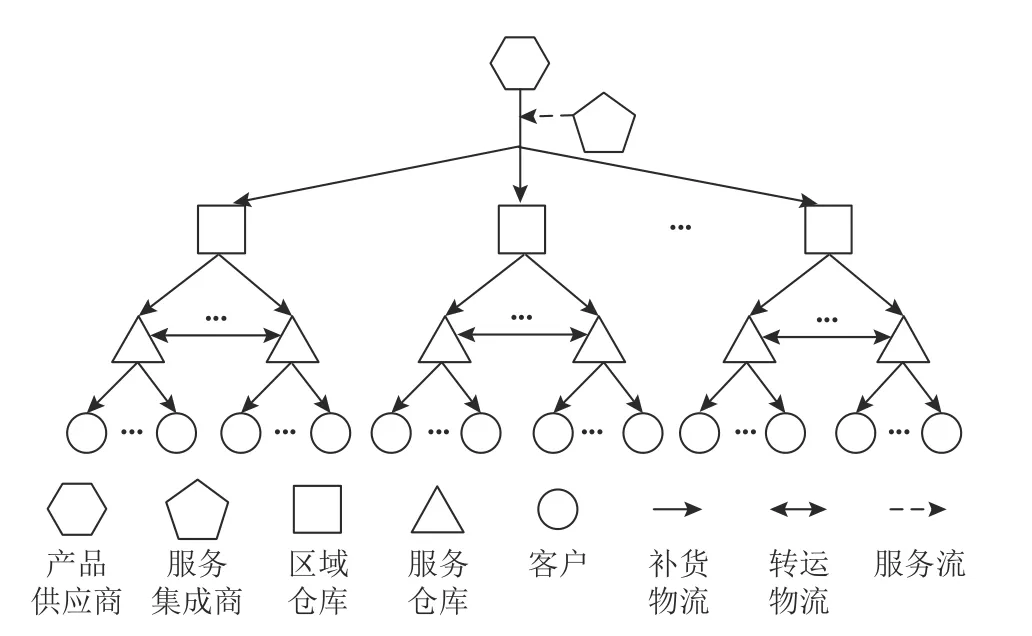
图1 高技术或成套复杂设备PSSC Figure 1 Large complex equipment PSSC

表1 PSSC各节点及其主要功能Table 1 Supply chain nodes and main function

决策者需从已知的候选区域仓库节点和候选服务仓库节点中选择合适的节点与产品供应商节点、服务集成商节点、客户节点共同构成PSSC网络，并选择合适的服务价格及服务水平匹配基础产品，实现为客户提供优质服务的同时PSSC利润全局最优。

为便于研究，本文假设：1) 产品的销售价格是固定的；2) 客户经过售前服务后决定是否购买产品，即产品的需求量不大于服务的需求量；3) 产品供应商有足够的能力满足产品需求。

3 考虑售前服务的PSSC优化模型

根据假设，只有通过售前服务，协商阐明产品性能和需求之间的一致性之后，客户才会决定是否购买产品。由于产品需求与价格、质量之间存在一定的相关性，因此服务提供商的售前服务水平及价格将对产品需求产生影响。在不考虑价格以外因素对售前服务需求影响的情形下，售前服务的需求函数为das=Ma−α1Ps+λsS。其中，Ma为客户a∈对于产品及服务需求的基本规模；α1为服务价格的敏感系数；λs为客户服务需求对服务水平的敏感系数。并且根据张旭梅等[11]的研究，服务影响客户需求的数学模型为da=das−α2Pp+λcS。因此，售前服务影响客户产品需求的计算公式为

其中，α2为产品价格的敏感系数；λp为客户产品需求对服务水平的敏感系数。

PSSC的总成本包括固定成本、补货成本、仓库库存成本、配送成本和库存转运成本。各成本计算公式如下所示。

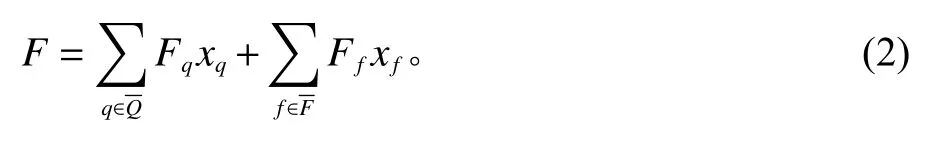
其中，Fq为区域仓库节点q的固定成本；Ff为服务仓库节点f的固定成本；xq为二进制变量，如果候选节点q被选为区域仓库为1，否则为0；xf为二进制变量，如果候选节点f被选为服务仓库，否则为0。

2) 补货成本。包括区域仓库补货成本和服务仓库补货成本。客户产品需求的变化将引起服务仓库节点补货数量的变化。服务仓库补货的成本为

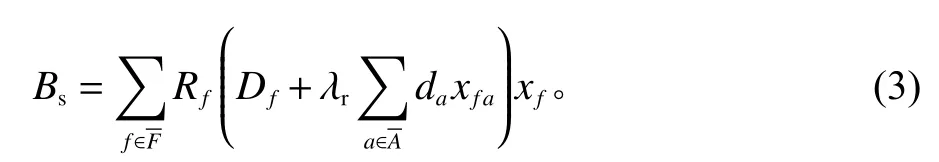
同理，服务仓库节点产品需求的变化将引起区域仓库节点补货数量的变化。因此，区域仓库补货成本为

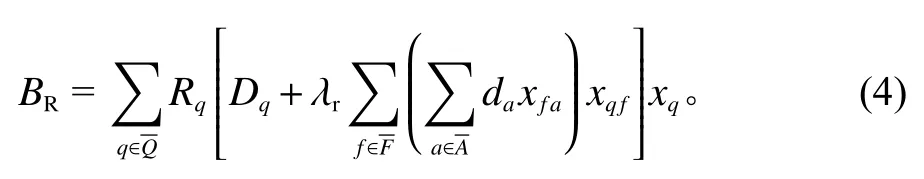
其中，Rf为服务仓库节点f的单位补货成本；Df为服务仓库节点f涵盖范围内产品基本补货数量；λr为补货数量对于市场需求的敏感系数；xfa为二进制变量，如果服务仓库节点f服务于客户节点a为1，否则为0；Rq为区域仓库节点q的单位补货成本；Dq为区域仓库节点q涵盖范围内产品基本补货数量；xqf为二进制变量，如果区域仓库节点q服务于仓库节点f为1，否则为0。

总补货成本为区域仓库补货成本和服务仓库补货成本的总和，因此总补货成本为算平均库存量的公式为，其中，λ为库

3) 库存成本。包括区域仓库节点的库存成本和服务仓库节点的库存成本。区域仓库节点q的总需求服从正态分布N(µq,σq2)。根据Ryzin[12]的研究，计存周期；Zα为安全库存系数；L为仓库的提前期。服务仓库产品需求的变化将引起区域仓库节点q的库存变化。因此，区域仓库的库存成本为

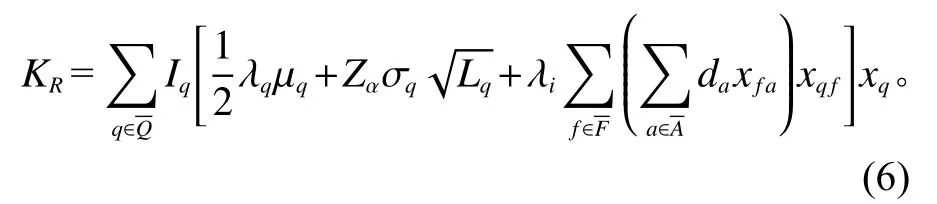
其中，Iq为区域仓库节点q的单位库存成本；λq为区域仓库节点q的库存周期；Lq为区域仓库节点q的提前期；λi为仓库库存对于市场需求的敏感系数。

服务仓库中节点f的总需求服从正态分布N(µf,σf2)。根据Sun等[13]以及Chen等[14]的研究，在仓库部分库存共享的情况下，库存为共享部分的转运量为其中，为未共享库存时的安全库存；而为共享时的安全库存；β为库存共享率。这表示由于库存共享而减少了库存量。客户产品需求变化将引起服务仓库节点f的库存变化。因此，服务仓库的库存成本为

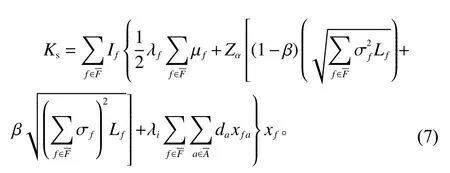
其中，If为服务仓库节点f的单位库存成本；λf为服务仓库节点f的库存周期；Lf为服务仓库节点f的提前期。

库存总成本为服务仓库库存成本和区域仓库库存成本的总和为

4) 转运成本。库存在服务仓库节点之间共享，因此产生一定的转运成本，即每单位产品的转运成本乘以转运数量。每单位产品的转运成本为t。根据上述公式转运成本为

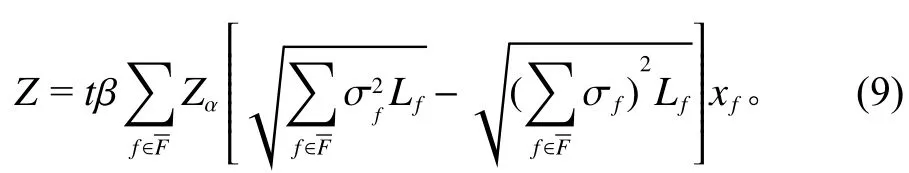
5) 配送成本。包括从产品供应商到区域仓库，从区域仓库到服务仓库的货物运输总成本。每个节点的配送成本可以用单位配送成本乘以配送数量来表示。Axsater[15]提出，可以使用需求平均值代替随机需求。因此，每个区域仓库和服务仓库的配送成本等于单位配送成本乘以相应的仓库补货数量。每个节点的产品需求等于服务影响下产生的新需求和原有需求之和。因此，总配送成本可以通过将每个区域仓库和服务仓库的配送成本相加进行计算。

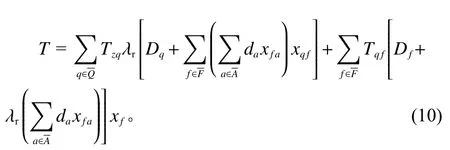
其中，Tzq为单位产品从产品供应商节点z到区域仓库节点q的配送成本；Tqf为单位产品从区域仓库节点q到服务仓库节点f的配送成本；Tfa为单位产品从服务仓库节点f到客户节点a的配送成本；xfa为二进制变量，如果服务仓库节点f服务于客户节点f为1，否则为0。

6) PSSC的收益。单位产品生产成本为c，服务集成商的服务成本系数为µ，服务集成商提供服务级别S的服务成本为。总收益为产品提供商和服务集成商收益的总和。根据上述可知，收益函数为

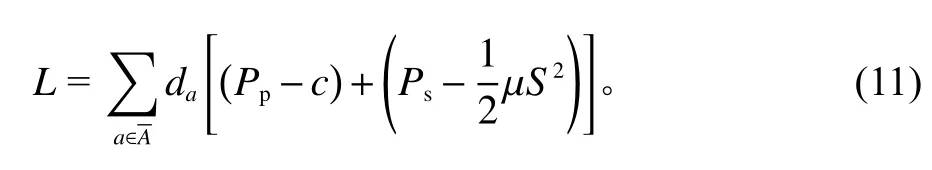
结合上述所有公式，考虑售前服务的PSSC优化模型为

式(13)约束区域仓库只能向下游节点的服务仓库提供配送服务。式(14)约束服务仓库只能向下游节点的客户提供配送服务。式(15)约束每个服务仓库只能由1个区域仓库进行配送服务。式(16)约束每个客户只能由1个服务仓库进行配送服务。式(17)约束服务仓库节点的需求应小于或等于区域仓库节点q到服务仓库f的运输能力，TCqf为区域仓库节点q与服务仓库节点f之间的运输能力。式(18)约束客户节点的需求应小于或等于服务仓库节点f到客户a的运输能力，TCfa为服务仓库节点f与客户节点a之间的运输能力。式(19)约束决策变量S相对应的成本小于决策变量Ps且大于Ps的1/3，以满足为客户提供优质服务的最小服务成本。式(20)约束该模型中的决策变量xq、xf、xqf、xfa为二进制变量。

4 基于具有约束推理的双层嵌套遗传算法的模型求解

考虑售前服务的PSSC优化模型是一个混合整数规划模型。由于现实生活中的多级供应链通常包含数百或数千个节点，因此这是一个大规模优化问题。联合优化服务和PSSC的协调配置是双层模型之间的迭代决策过程。双层优化解决方案往往比单级优化问题更复杂[16]。通常，即使双层优化模型是线性的，它也是一个NP-hard问题[17]。传统的解决方法包括线性情况的极点值法[18]、基于Karushe-Kuhne-Tucker(KKT)条件的分支定界法[19]、遗传算法等等。本文提出一种具有约束推理的双层嵌套遗传算法来解决联合优化模型。算法主要流程如图2所示。

图2 算法流程Figure 2 Algorithm flowchart

其中的关键步骤如下。

1) 编码。GA实施的关键是通过被称为染色体的有限长度字符串表示要解决的问题。考虑服务水平、服务集成商的服务价格以及后续节点的选择。本文定义了两种染色体：上级染色体(UC)和下级染色体(LC)。如图3所示，1个UC由代表服务价格和服务水平的基因以及多个LC组成，代表一种PSSC方案。其中LC的数量等于候选仓库节点的数量。如果1个LC中的所有基因均为0，即不选择该候选区域仓库节点。LC为相邻基因组成的一个基因组，代表一个候选区域仓库节点及其下属服务仓库节点的选择方案。LC的长度为候选服务仓库节点的数量。就LC1而言，LC1中的基因代表相应节点是否选择(已选择为1，否则为0)。

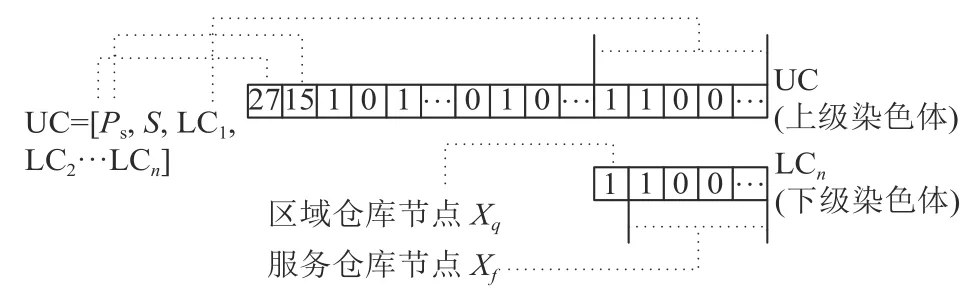
图3 PSSC的GA编码Figure 3 GA encoding for PSSC

2) 适应度评估。第3节中描述的目标函数用于染色体适应度评估。目标函数值越高，个体适应度越高。记录适应度最高的染色体及其相应的数值。与先前的记录数值进行比较，如果该值大于之前记录值，则更新记录。否则，将当前种群中适应度最小的染色体替换为记录中的染色体。

3) 交叉。GA中的交叉是指选择两条亲本染色体以概率交换其部分基因。本文交叉处理分为上级染色体交叉与下级染色体交叉。上级染色体交叉：(1) 随机选择父本染色体上的LC染色体或选择对应服务价格、水平的染色体；(2) 2个亲本之间交换2个亚染色体。下级染色体交叉：(1) 随机选择LC染色体上的两个位置；(2) 2个亲本之间交换2个亚染色体；(3) 确定两个片段之间的映射关系。

4) 变异。变异在交叉后应用于每个后代，发生突变的可能性很小。从后代染色体中随机选择1至3个基因进行变异。如果所选基因是代表价格或服务水平的基因，则改变其数值。 如果所选基因位于后代染色体的LC中，则改变基因对应二进制变量数值，为1则变为0，为0则变为1。

5) 约束处理。检查新生成的染色体并根据参数之间的约束关系对其进行修正。如果表示服务水平的基因值高于服务价格的基因值，调整代表服务水平的基因以满足模型约束。并且，检查染色体中的每个LC。如果LC中代表区域仓库的基因的值为0，检查LC中代表服务仓库的基因是否为0。如果为1，则将其修正为0。

6) 终止。繁殖、交叉和变异的过程反复进行，直到种群收敛或达到一定数量的世代为止。

本文利用约束推理作为预处理或处理步骤，通过分析参数之间的约束来减轻计算负担。如前所示，PSSC中存在服务配置约束和设施约束。使用约束条件推理技术(如约束补偿)，通过域修剪和约束条件传播来减少PSSC的搜索空间。例如，处理服务水平和服务价格的编码时，使与服务级别相对应的成本小于服务价格且大于服务价格的1/3(即满足最小服务成本)。

5 数值算例

为了验证所提出算法在考虑售前服务影响的PSSC优化问题中的实用性和有效性，本文使用一个具体的案例进行计算，并与经典双层嵌套遗传算法进行分析对比。该案例的数据参数来自某生产船舶细水雾喷淋系统的建材公司。该公司的多级PSSC网络具有1个产品供应商、1个服务集成商，3个区域仓库节点(从5个候选区域仓库节点中选出)和6个服务仓库节点(从14个候选服务仓库节点中选出)。售前服务的定价范围是9 ～ 30，服务水平等级范围是3～ 8，其他参数如表2 ～ 4所示。通过计算，考虑售前服务影响的PSSC优化结果如下所示。图4表示该算法的收敛过程，横坐标为迭代次数，纵坐标为与最优解相对应的PSSC利润，算法在310代收敛到最优。图5为最优服务价格和服务水平搜索过程，从中可以看出，最优服务价格为14，最优服务水平为4。

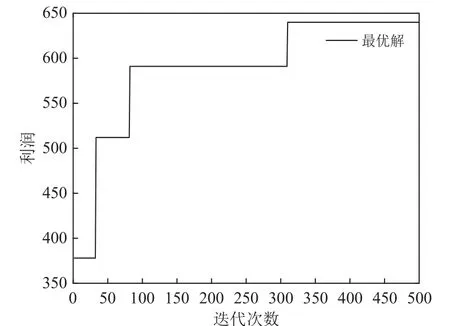
图4 具有约束推理的双层嵌套遗传算法最优解搜索过程Figure 4 Searching process of optimal solution by genetic algorithm

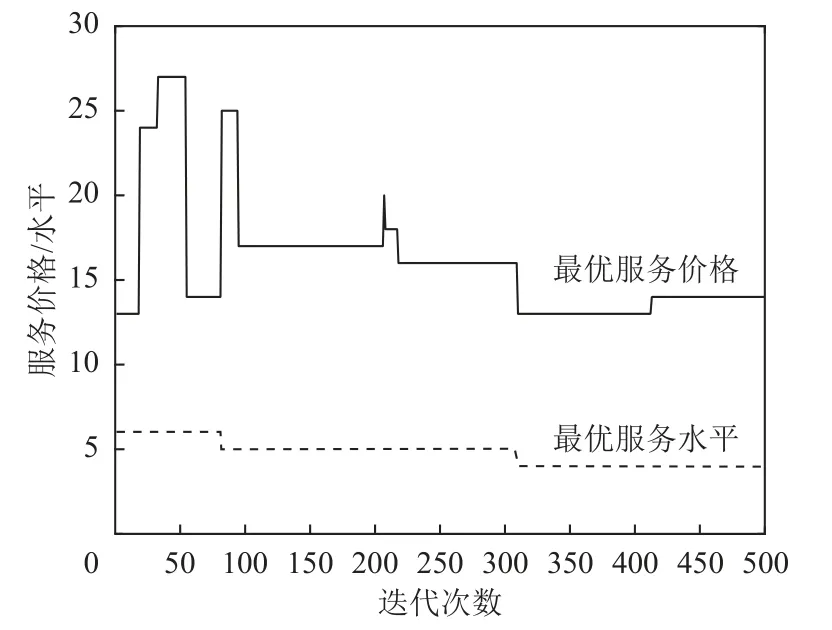
图5 最优服务价格和服务水平搜索过程Figure 5 Searching process of optimal service price and level of genetic algorithm

表2 区域仓库节点参数Table 2 Regional warehouse node parameter table

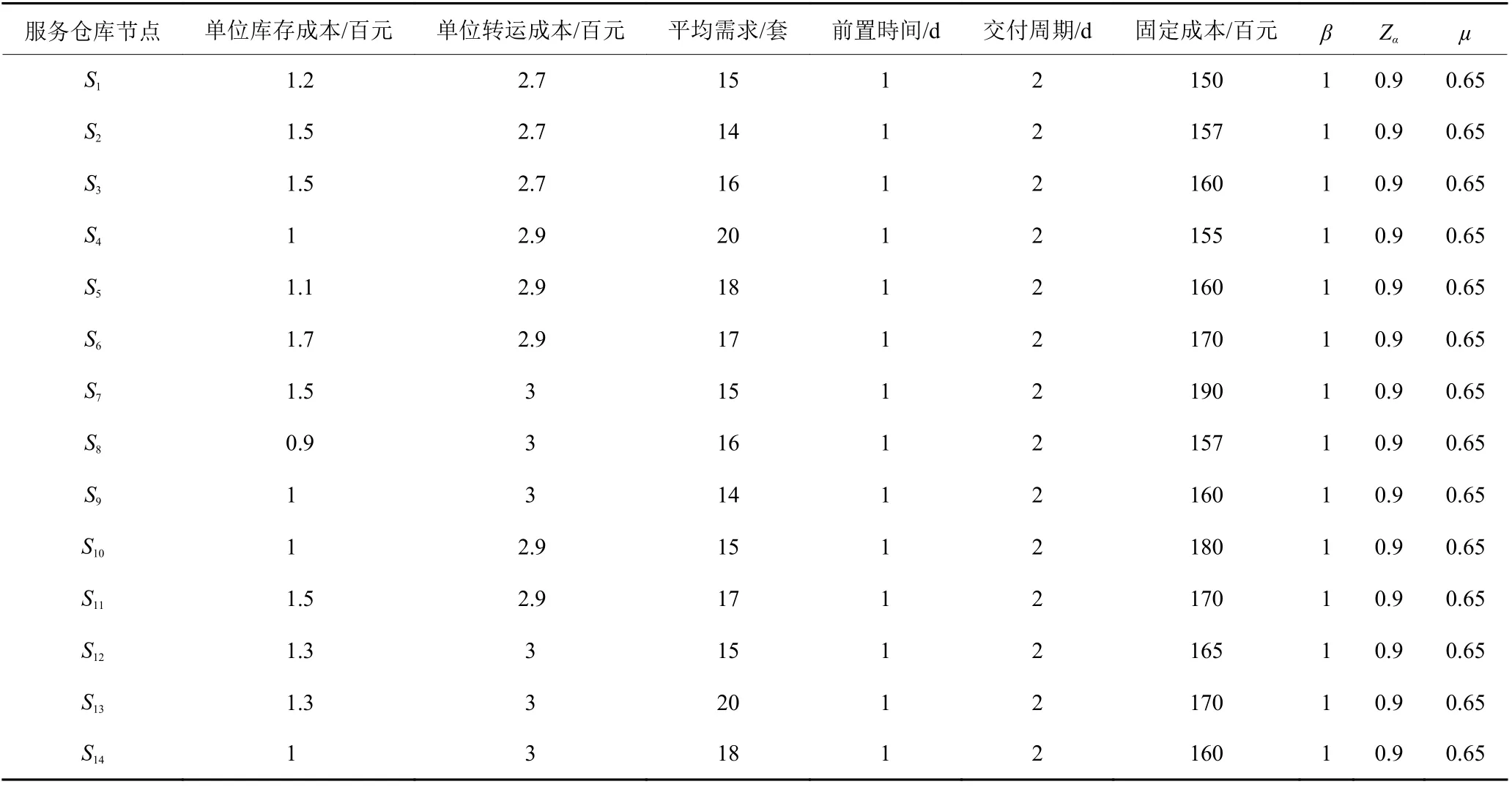
表3 服务仓库节点S1-S14参数表Table 3 Service warehouse node S1-S14 parameter table

表4 区域仓库节点至服务仓库节点的单位配送成本Table 4 Unit delivery cost from regional warehouse node to service warehouse node

基于此结果对应的染色体信息，可以知道PSSC的最优利润为647。从5个候选区域仓库中，选择了R1、R3、R5。在14个候选服务仓库中，选定了S1、S2、S7、S9、S13、S14，其PSSC网络结构图如图6所示。

图6 该案例的最优PSSCFigure 6 Brief PSSC network diagram

5.1 算法有效性分析

为验证提出算法的实用性及有效性，首先采用经典嵌套遗传算法进行对比，该算法计算结果如图7所示。算法在340代收敛，且最优解为593。因此，本文所提出的算法在收敛速度以及求解最优值方面均优于经典嵌套遗传算法.

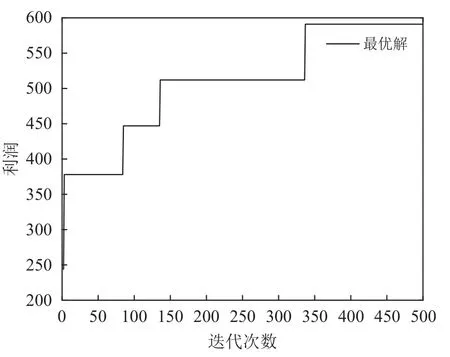
图7 双层嵌套遗传算法最优解搜索过程Figure 7 Search process of the classical double nested genetic algorithm

其次，为进一步检测本文算法的搜索效率和有效性，本文通过设定不同的种群规模及遗传代数，并随机选择初始种群，多次进行计算。具体结果如表5所示。结果表明，对于恰当的种群规模或遗传代数，本文算法均能得到最优值，且运算效率较高。可以看出，随着种群规模扩大，计算时间趋于减少，最优值首次出现的时间也趋于提前，这说明扩大种群规模有利于降低算法的时间复杂性。需要额外说明的是，由于初始种群的生成和遗传操作具有随机性，最优值首次出现的代数并没有明显的规律性。即使种群规模和遗传代数完全相同，2次计算最优值首次出现的代数也未必相同。

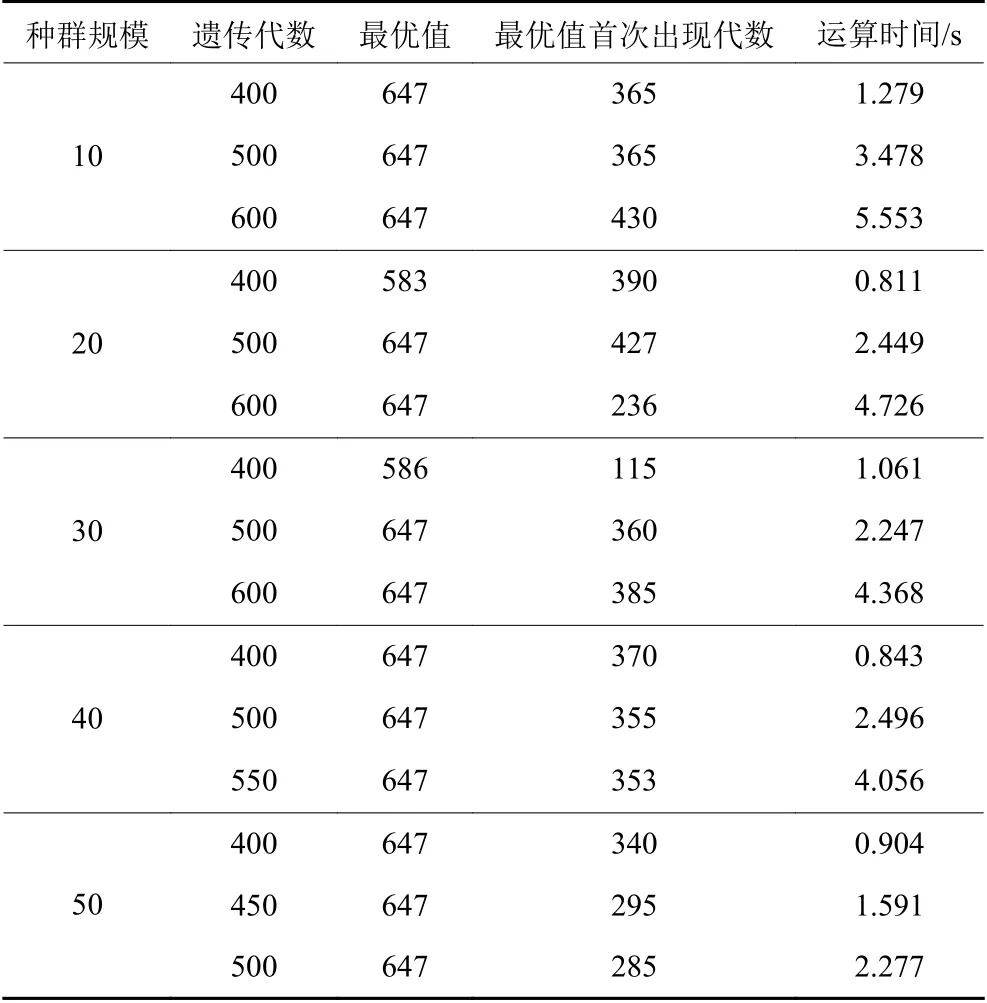
表5 算法结果Table 5 Algorithm result

6 结束语

本文研究了售前服务影响下的PSSC优化问题。从全局分析售前服务影响下PSSC变化，建立考虑售前服务水平及价格的PSSC网络优化模型，以服务集成商和产品供应商的全局利润最优解为目标得出最佳服务水平、服务价格以及PSSC网络结构，提出一种具有约束推理的双层嵌套遗传算法。本文通过计算某生产船舶细水雾喷淋系统建材公司的PSSC案例，并与经典嵌套遗传算法相比较，证明算法具有实用性，并进一步在不同种群规模和不同遗传代数设置条件下反复运行该算法以检测算法的搜索效率和有效性。结果表明，本文设计的遗传算法有效，且具有较好的搜索效率。本研究可作为企业相关PSSC决策的参考，有助于企业决策者在PSSC设计阶段进行服务水平、服务价格以及PSSC选址问题的决策，具有现实指导意义。目前本文的研究具有一定的局限性。比如假设产品价格是固定的，也没有考虑与其他企业的竞争问题。这些问题将在以后的研究中加以考虑。