时变路网下电动冷藏车配送路径优化研究

王玖河，安聪琢，郭田宇

(1.燕山大学 经济管理学院，河北 秦皇岛 066004；2.燕山大学 京津冀协同发展管理创新研究中心，河北 秦皇岛 066004；3.辽宁工程技术大学 工商管理学院，辽宁 葫芦岛 125105)

随着城市化进程不断加快，我国的交通日趋便利，但与此同时城市的交通拥堵问题也日益严重。在物流配送过程中，车辆的行驶速度和行驶时间受当前路况的影响较大，而基于车辆匀速行驶的静态路网假设的理想状态下所求解的最优路径问题与实际情况偏差较大，考虑时变路网下的车辆配送路径更加符合现实情况。面对当前环境污染严重、石油资源短缺等问题，传统燃油车的弊端日益显露，电动冷藏车凭借着环保、节能等优势在实现“最后一公里”的物流配送终端得到了广泛的利用。因此，研究时变路网下电动冷藏车的配送路径问题更加符合现实运输环境的需要，具有重要的理论意义和现实价值。

对于电动车辆的路径问题，国内外学者展开了广泛的研究。揭婉晨等[1]建立电动汽车车辆路径问题的混合整数规划模型，并采用改进的分支定界算法进行求解。Gerhard等[2]研究带时间窗和充电站的混合车辆路径问题，建立考虑车辆充电时间和充电地点的路径优化模型。Verma[3]提出一种带有时间窗和充电站的电动汽车路径问题，允许可用的充电站同时作为充电站和电池交换站。Keskin等[4]针对充电站容量有限这一实际情况，建立考虑车辆排队时间的带时间窗的电动汽车路径优化模型，并结合自适应大邻域搜索算法和混合整数线性规划解的数学算法进行求解。葛显龙等[5]针对电动汽车配送过程中的问题，建立考虑部分充电策略的EVRPTW模型，并利用混合模拟退火算法进行求解。

在考虑时变路网下的车辆路径问题的研究上，Kok等[6]考虑交通拥堵状况以及驾驶时间规则等因素，引入时变网络理论，建立以驾驶时间最短为目标函数的路径优化模型。Tas等[7]研究具有软时间窗和随机出行时间的车辆路径问题，建立以运输成本和服务成本最小化为目标函数的数学模型，并利用分支定界算法对模型进行求解。吴瑶等[8]考虑交通的时变性，针对易腐食品，建立时变路网下的生产−配送优化模型，并设计了改进的遗传算法对模型进行求解。张济风等[9]研究冷链物流配送的路径优化问题，并利用模拟退火算法计算出在时变交通下的满足总配送成本最低的最优路径。Zheng[10]以配送成本最小化和平均不满意度最低为目标函数，建立基于时变交通流的多模糊时间窗车辆路径问题模型。付朝晖等[11]以生鲜配送为研究对象，设计时变路网下的车辆行驶时间计算方法以及考虑生鲜鲜活度的开放式时变车辆路径优化模型，并设计改进的蚁群算法进行求解。

综上，大多数学者都是将电动车辆的路径优化问题与时变路网下的车辆路径问题独立开来进行研究。对于电动车辆路径问题的研究中，多数都是基于恒定速度的静态路网假设下进行研究，忽视了交通路网的时变特性对电动车辆实际配送过程中的影响，导致求解结果可能与实际情况有较大误差。因此，本文将电动车辆的路径优化问题与时变路网下的车辆路径问题相结合，同时引入多模糊时间窗约束，建立考虑时变路网的电动冷藏车配送模型，运用AP聚类算法对配送区域进行划分，提高配送效率，并设计改进遗传算法对模型进行求解，最后通过设置算例将静态网络与时变网络下的配送成本进行对比，验证模型及算法的有效性。

1 问题描述与假设

1.1 问题描述

在现实生活中，交通路网具有时变特性，车辆的行驶速度受当前所处时段的影响。本文研究时变路网下的车辆配送路径，将配送过程看作若干个时段，根据各个时段交通拥堵状况的不同，每个时段的车速也可能不同，如图1所示。时段划分越细，求解结果越准确。本研究中采用电动车辆进行生鲜配送，且在配送过程中车辆电量不足以行驶至下一需求点时，需到就近的充电桩进行充电。同时，相较于传统VRPTW模型中的单时间窗约束，本文引入多模糊时间窗约束，旨在满足车辆载重约束、电量约束、时间窗约束等条件下，求解使得总配送成本最小的最优路径。

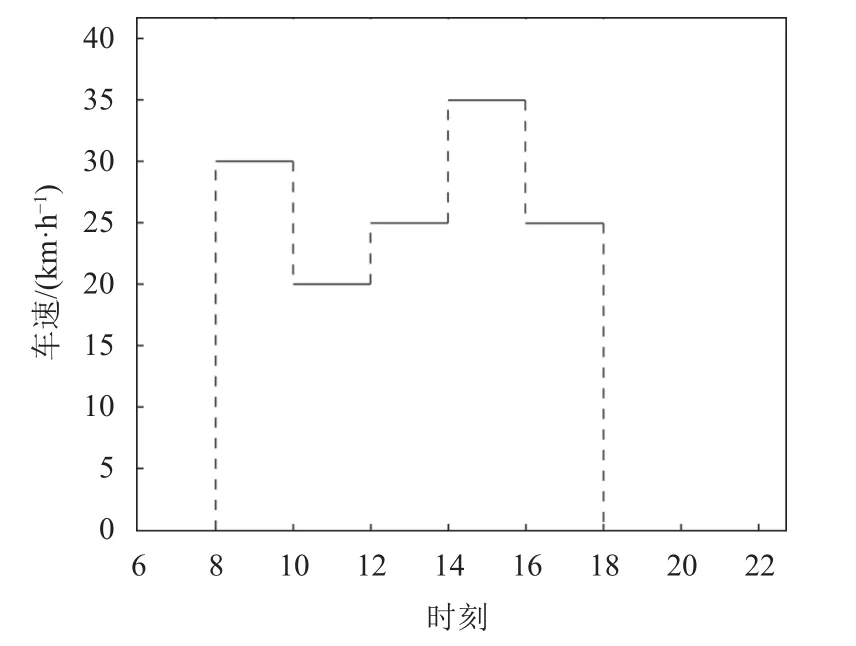
图1 各时段速度对应示意图Figure 1 Schematic diagram of the corresponding speed in each period

1.2 模型假设

1) 只有一个配送中心，所有车辆均从配送中心出发，且配送完成后返回配送中心；

2) 每个需求点只能有一辆车进行配送；

3) 不同配送区域间车辆不可跨区域配送；

4) 充电桩的电量足够车辆需要；

5) 任一客户点的需求量均小于车辆最大载重量；

6) 同一需求点的不同时间窗不会重合；

7) 交通路网时变区间为20 min。

2 符号设定及模型构建

2.1 主要符号设定

K为车辆编号集合，K={1,2,···,p}，k∈K；

I为节点编号集合，I={0,1,2,···,i}，其中，0表示物资分配中心;

H为客户的时间窗编号集合，H={1,2,···,h};R为充电桩编号集合，R={1,2,···,r}；

N为客户点编号集合，N={4,5,···,n}；

为时段的集合，Tn′={T0,T1,T2,···,Tn}，其中[Tn−1,Tn]表 示第n个 时段；

dij为 任意节点i到 节点j的距离(i≠j)；

a为单位车辆单位时间的早到惩罚成本；

b为单位车辆单位时间的延迟惩罚成本；

L为车辆的最大载重量；

Qi为 客户i的需求量；

t0为发车时刻；

ti为到达节点i的时刻；为客户i的 第 ∂个时间窗要求，其中，为客户i所能接受的最早服务时间，为客户i所期待的最早服务时间，为客户i所期待的最晚服务时间，为客户i所能接受的最晚服务时间。

决策变量如下。

2.2 模型构建

2.2.1 时变路网模型

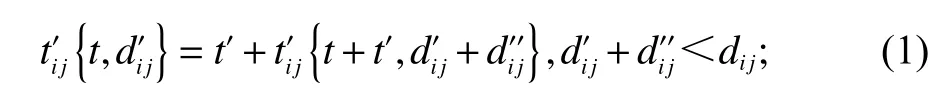
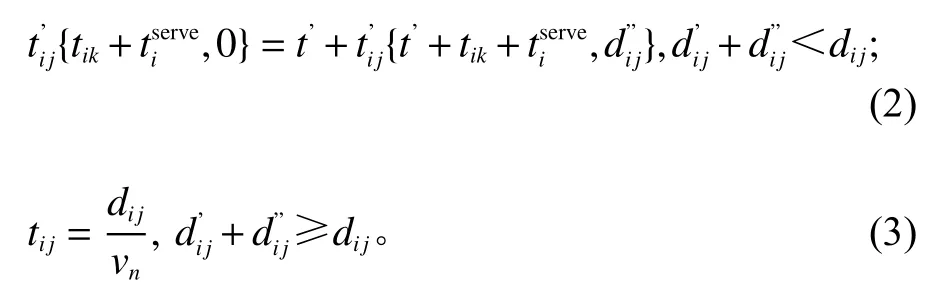
其中，tij表 示行驶完i、j段 所需时间；tiserve表示客户i的 服务时间；tik表 示车辆k到客户i的 时间；t表示此时所处的时刻；Tn表 示时刻t所 对应的时段；t’表示Tn时 段的剩余时间，即Tn−t，其中t∈[Tn−1,Tn]；di j表 示i与j之 间 的 距 离；di’

j表示车辆已经行驶的距离；vn表示Tn时 段所对应的速度；表示在t时刻车辆已经行驶了di’

j距 离，继续行驶完dij所需要的时间；di’’j表

示t时刻已行驶了di’j距离，继续以速度vn行驶完Tn中的剩余时间，所行驶的距离。

式(1)、(2)表示物流节点i与j之间的行驶时间横跨多个时段的情况。其中，式(1)表示在配送完客户i后去往客户j的途中，已经行驶了di’j距离，继续行驶到客户j所需时间；式(2)表示在客户i处服务完毕后(还未出发)继续行驶到下一客户j处所需时间；式(3)表示在一个时段之内即可完成i与j之间的配送时所需要的时间。

2.2.2 充电耗电模型

同种类型的电车在行驶过程中，耗电量与货物重量和行驶速度有关。本文引用目前广泛应用的功率及功耗计算方法[12]，则功率计算公式为

其中，Pkv(Q)为 车辆k载重为Q且以速度v行驶时的功率；M为车辆自重；g为重力加速度，本研究取 9.8 m/s2；f为汽车滚动阻力系数；Cd为空气阻力系数；S′为 汽车迎风面积； η为传动系统机械效率。

功耗计算公式为

若车辆k配送完客户i后电量不足以行驶到下一客户j，则需要到距离最近的充电站充电，充电时间为

2.2.3 配送成本模型

式(7)表示完成配送任务所需的固定成本，其中P1为单位车辆固定成本(元/辆)；式(8)表示完成配送任务所需的车辆行驶成本，P2为单位车辆单位距离行驶成本(元·km−1·辆−1)；式(9)表示完成配送任务所需的耗电成本，P3为单位车辆耗电成本(元/kWh)；式(10)表示完成配送任务所需的制冷成本，P4为单位车辆制冷成本(元/kcal)，R′为 热转换系数，S为车厢表面积，φ为车厢内外温差，λ为车厢劣化程度；式(11)表示完成配送任务所需的充电成本，P5为单位充电成本(元/kWh)，Em为电池最大容量(kWh)，为车辆k到 充电桩时所剩电量(kWh)，uik为0或1的决策变量；式(12)表示惩罚成本，tik为 车辆k到达客户i的时间；式(13)为模型的目标函数，即求最低总配送成本。

2.2.4 约束条件

式(14)表示车辆不能超载；式(15)表示一个客户只能被一辆车服务，且所有客户配送完毕，车辆必须返回配送中心；式(16)表示同一客户的不同时间窗区间不能重合；式(17)表示车辆到达客户点的时间应处于任意一个时间窗范围内；式(18)表示车辆经过充电桩i时的电量变化，表示车辆到达充电桩i时的电量，表示离开节点i的电量；式(19)表示车辆经过节点i后的时间变化，表示车辆k离开节点i时的时间，tik表示车辆k到达充电桩i时的时间；式(20)表示车辆k从离开节点i至到达节点j过程中的电量变化，表 示车辆k离开节点i时的剩余电量，Ejk表示车辆k到达节点j时的剩余电量，B为一个数值很大的常数；式(21)表示车辆k到达节点i与离开节点i的时间变化；式(22)表示车辆所剩电量必须大于最低行驶变量。式(23) ～ (27)为相关决策变量，分别表示车辆k从i行 驶到j，则xijk为1，否则为0；客户i由 车辆k配送，则yik为1，否则为0；车辆k从配送中心发车，则x0ik为 1，否则为0；车辆到达客户i处于第 ∂个时间窗内，则为1，否则为0；车辆k在充电桩i充 电，则uik为1，否则为0。

3 算法设计

目前对于常规VRP问题的研究较为成熟，常用的求解算法有遗传算法[13]、蚁群算法[14]、模拟退火算法[15-16]等。相比于常规的VRPTW问题，本文的模型中引入了电车充电模型及多时间窗的情况，采用AP算法对客户点进行聚类后，对各个区域分别使用遗传算法进行求解。

3.1 AP聚类算法

仿 射 传 播 聚 类 算 法(affinity propagation)简 称AP聚类算法，是基于数据点间的“信息传递”的一种聚类算法。算法的基本思想：将全部样本看作网络节点，通过网络中各条边的消息传递计算出各样本的聚类中心。聚类过程中，共有两种消息在各节点间传递，分别是吸引度(responsibility)和归属度(availability)。通过在点之间传递信息，通过不断地传递信息，最终选出代表元以完成聚类[17]。AP算法通过迭代过程不断更新每一个点的吸引度和归属度值，直到产生m个高质量的exemplar(类似于质心)，同时将其余的数据点分配到相应的聚类中。

其中有两个重要参数，分别为吸引度矩阵R=[r(i,k)]，归属度矩阵Ψ =[ψ(i,k)]，均为N阶矩阵，矩阵更新公式为

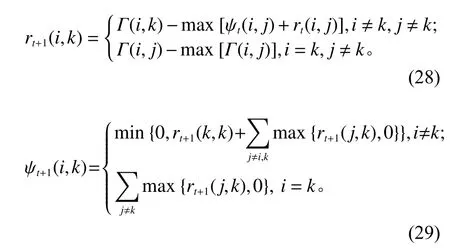
式(28)为吸引度矩阵更新公式，表示数据点k适合作为数据点i的聚类中心的程度；式(29)归属度矩阵更新公式，表示数据点i选择数据点k作为其聚类中心的合适程度。本文为了避免迭代更新的过程中出现不可控震荡，也为了加快计算速度，在上述操作后引入衰减系数λ ，λ为(0,1)之间的某实数，一般取0.5。衰减公式为

式(30)为吸引度矩阵的衰减公式；式(31)为归属度矩阵的衰减公式。

在迭代的过程中，要先对吸引度矩阵进行迭代，再使用迭代后的吸引度矩阵去计算归属度矩阵，最后对其进行衰减，完成一次迭代。重复迭代的过程，直至达到设置的最大迭代次数或聚类结果。经多次迭代不再改变后，跳出循环，结束算法。

3.2 改进遗传算法

3.2.1 染色体编码及形成初始种群

本文选用实数编码，染色体中的基因代表各个物流节点(配送中心、充电桩、客户点)，其中0代表配送中心，1、2、3代表充电桩，其余代表客户点。在染色体中实数的顺序代表了配送车辆的路径。例如，有一个配送中心、3个充电桩和10个客户点，则染色体至少需要有25个基因位。若算法运行结果为0-7-4-6-9-8-2-5-10-0，则表示车辆从配送中心出发，依次配送客户点4、客户点6、客户点9和客户点8，并在配送完客户点8之后返回充电桩2进行充电，之后继续配送客户点5和客户点10，配送完毕后返回配送中心。初始种群的形成，首先随机生成一个NP×CN的矩阵，NP代表种群规模，CN代表染色体长度，这里的染色体中不包含配送中心及充电桩的基因位，仅代表各个客户点，例如，某染色体为4-7-9-6-5，意为配送顺序为客户点4、7、9、6、5，但并未计算在配送途中何时需返回充电桩进行充电以及返回哪个充电桩，确定充电桩的工作在计算适应度的操作中完成。

3.2.2 计算适应度

在初始种群初步形成之后，需要根据各条染色体适应度的大小决定进入遗传操作的优秀父代染色体，由于本研究的优化目标是成本最小，故适应度函数取成本函数的倒数，即

计算适应度之前，需要确定车辆配送过程中返回充电桩的时刻。在初始种群形成后，得到了一个VRP问题的初始解，对应染色体中并不包含代表充电桩的基因。由于车辆本身的电量有限，所以形成的初始解可能为不可行解，因此需要在合适的位置插入充电桩，使其变为可行解。在充电桩的插入策略中，若车辆通过节点i后，其电量不足以行驶至下一个节点j，则称节点i为整条路径中的中断点，在算法识别到中断点时，需要在中断点后插入充电桩。

考虑到极限情况的存在，车辆在配送完任意一个客户点之后都有可能进行充电，所以在编程的过程中，任意两个代表客户点或者配送中心的基因位之间，都必须存在一个空基因位用来储存可能存在的代表充电桩的基因，在染色体的两端还需要加入两个基因位来储存代表配送中心的基因。在上述条件下，用于计算适应度的染色体长度需为2+客户点数量+(2+客户点数量−1)，即2×客户点数量+3。在车辆按照初始种群染色体中的基因顺序行驶完任意一个节点后，若满足式(20)，则不需加入充电桩。若不满足，则需在该节点与下一节点之间的空基因位加入代表充电桩的基因，判断该点与所有待选充电桩的距离，并选择代表最近的充电桩的基因，充电后将电量补满继续行驶，直至遍历完所有节点，完成新染色体的构建。使用式(32)计算新染色体的适应度，并选择适应度最大的个体进行后续进化操作。

3.2.3 选择、交叉和变异

为了确保最优个体可以进入子代，本文选用保留最佳个体与轮盘赌选择法相结合的方式选择染色体[18]。具体操作过程如下。

步骤 1以适应值函数的值为序，使染色体由好到坏进行重排，fh越 大，则染色体h越好，其序号越小。设参数a∈(0,1)给定，定义基于序的评价函数为

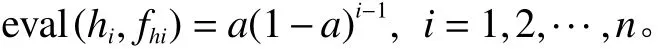
其中，i=1时 染色体最好，i=n时染色体最差。选择序号为1的染色体复制到下一代，其余染色体按以下步骤操作。

步骤 2对每个染色体hi计 算累计概率pi。

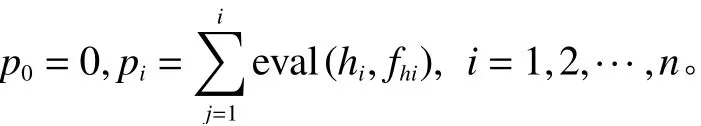
步骤 3产生随机实数r∈(0,pn).

步骤 4若pi−1＜r＜pi，则选择第i个 染色体hi。

步骤 5重复步骤 3和步骤 4，n−1次 ，得到n−1个染色体。

选择两点交叉，并对常规变异算子进行改进，将其分为交换变异、逆转变异和插入变异。具体操作过程如下。

步骤 1交换变异，即常规的变异算子，在染色体内随机取两个不稳定基因进行互换。

步骤 2逆转变异，即随机选取逆转区间，对逆转区间的基因取倒序后重新计算该染色体的适应度，并与原适应度比较，若适应度得到提升则保留新染色体，否则保留原染色体。逆转操作有助于提高种群的多样性，防止陷入近亲繁殖。

步骤 3插入变异，考虑到轮盘赌选择法容易漏掉小概率个体，故在逆转变异后进行插入操作，将按适应度降序排列染色体的前n条(n为父代与子代种群规模的差值)选中，与上述步骤形成的子代种群结合，形成新的种群。示例如下。

插入前：

父代种群

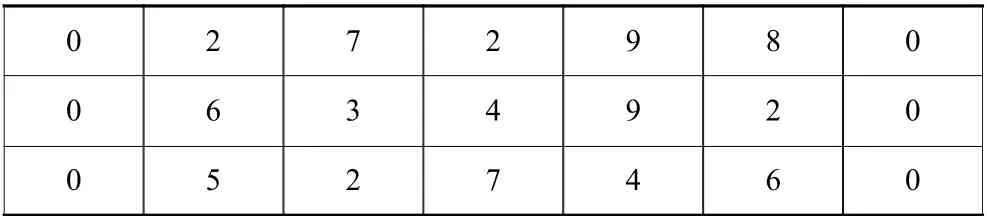
0 2 7 2 9 8 0 0 6 3 4 9 2 0 0 5 2 7 4 6 0

子代种群

0 9 8 5 6 3 0 0 7 4 2 8 6 0

假设父代种群3条染色体对应适应度分别为9、12、8，进行降序排列后为12、9、8，分别代表第2、1、3条染色体。

插入后

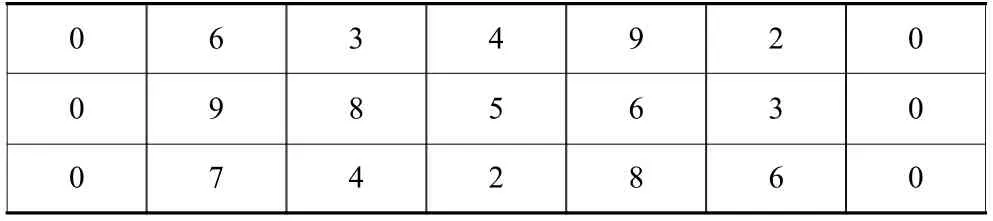
0 6 3 4 9 2 0 0 9 8 5 6 3 0 0 7 4 2 8 6 0

4 算例分析

4.1 参数设置

本文假设某企业为X市生鲜零售点配送生鲜产品，共有1个配送中心、3个充电桩和20个客户点。其中，0代表配送中心；1 ～ 3代表充电桩，4 ～ 23代表客户点。同时，为了更加贴合实际，各节点之间采用直线距离乘迂回系数代表实际距离，交通路网更新时段设置为20 min，发车时间为早8:00，出发时默认满电。各参数设置如表1所示。

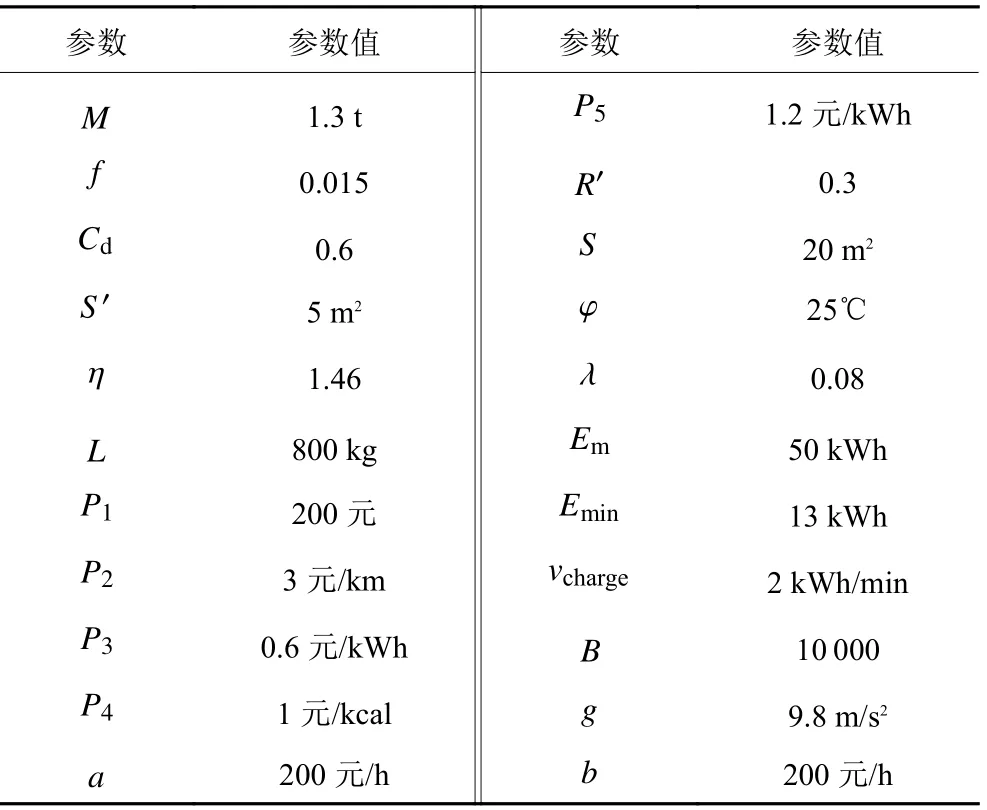
表1 参数设置Table 1 Parameter settings

各个时段对应的平均车速如表2所示。

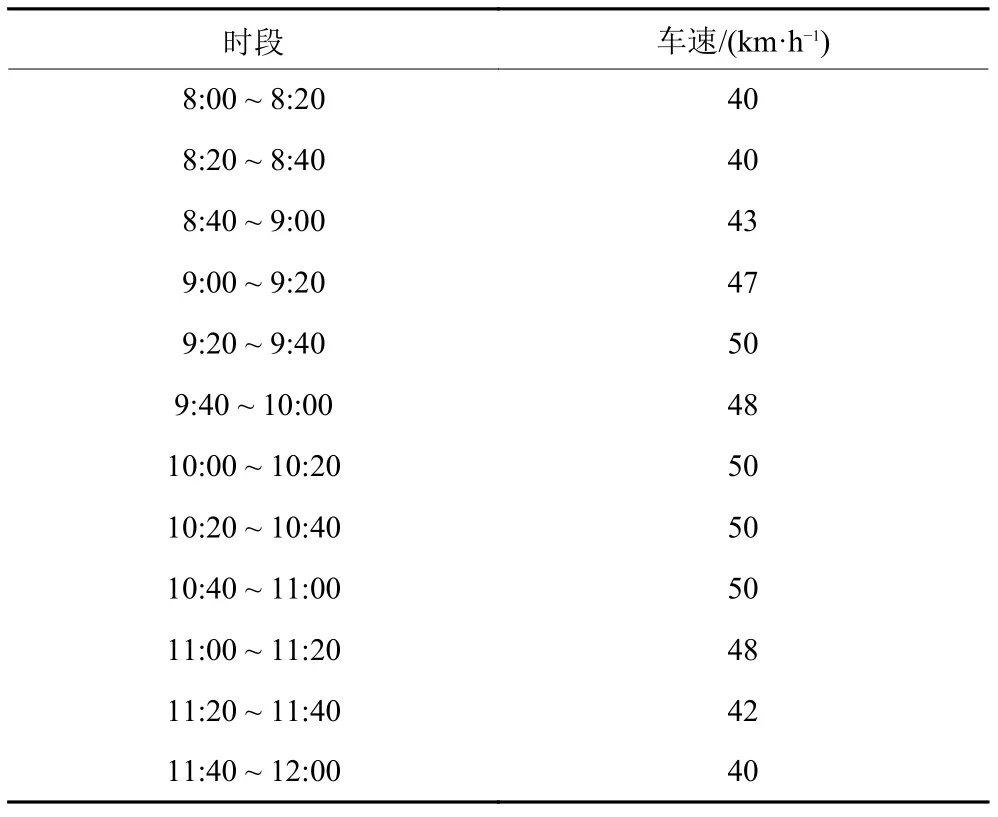
表2 各时段车速对应表Table 2 Corresponding table of vehicle speed in each period

配送中心、充电桩和客户点坐标数据如表3所示。

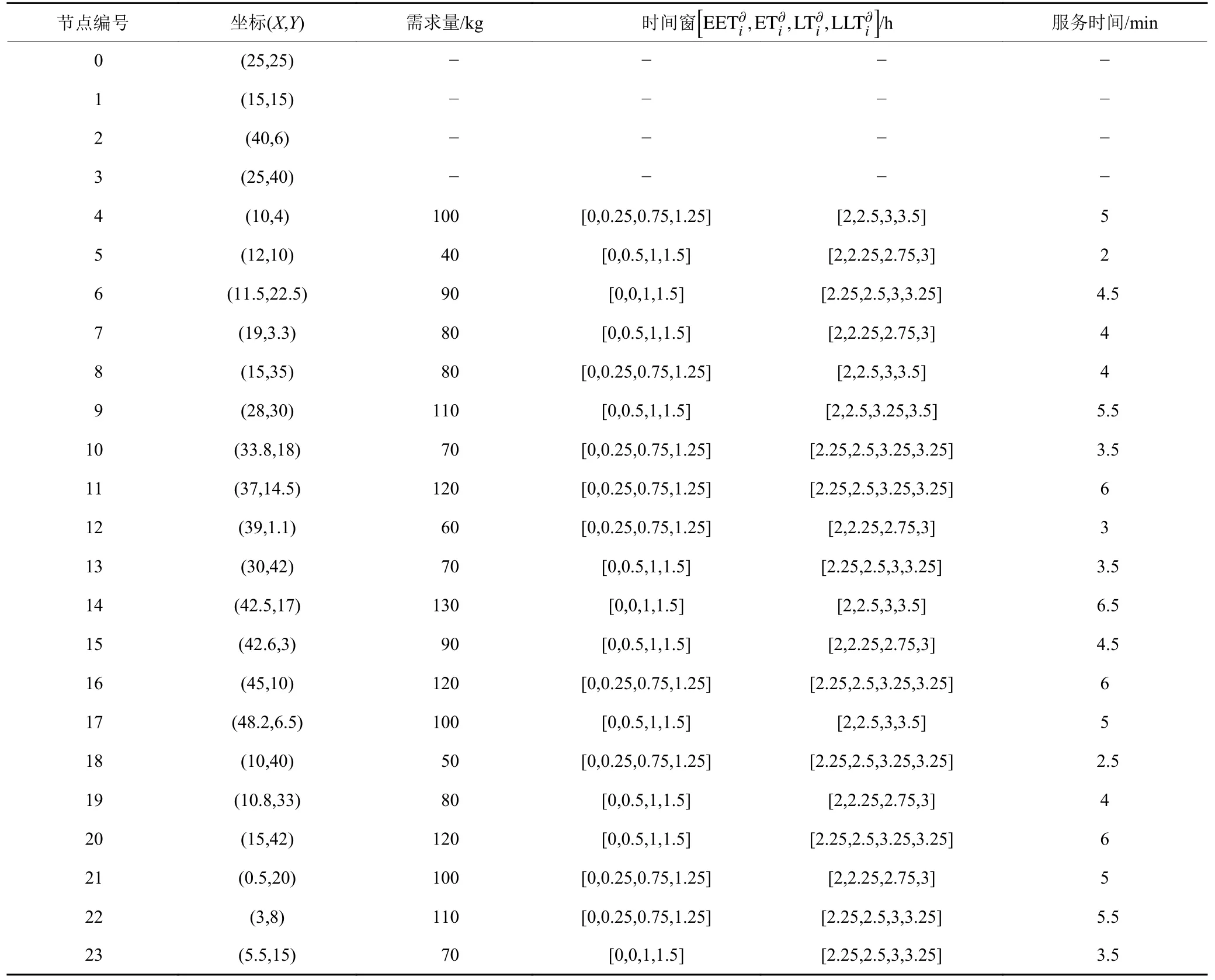
表3 配送信息Table 3 Distribution Information

4.2 聚类结果分析

将20个客户点坐标代入式(28) ～ (31)，设置最大迭代次数为500，当不变迭代次数为50时，输出聚类结果。运用Matlab编程计算可知，共聚类为3簇，聚类的合适度(tmpnetsim)为 −4.183 6e+03，相似度(net similarity)为 −4 183.64。第1簇客户点编号(区域1)为8、9、13、18、19、20；第2簇客户点编号(区域2)为4、5、6、7、21、22、23；第3簇客户点编号(区域3)为10、11、12、14、15、16、17。聚类图像如图2所示。

图2 聚类效果图Figure 2 Clustering effect diagram

4.3 路径优化结果分析

遗传算法参数设置如下。种群数量100，最大迭代次数200，交叉概率0.9，变异概率0.05。车辆行驶成本如表4所示，车辆行驶路径及时间点如表5所示。所有车辆固定成本均为200元。

表5 配送路径Table 5 Distribution path

配送路径图如图3。

图3 配送路径图Figure 3 Distribution path diagram

由表4可知，本次配送共派出3辆车，每辆车负责一个配送区域，负责区域1、2、3的车辆配送成本 分 别 为768.185 0元、1 176.721 1元 和845.177 5元，则配送总成本为2 790.083 6元。

表4 配送结果及路程Table 4 Path optimization results

4.4 对比研究

4.4.1 动态−静态对比

为了检验模型的有效性，本文将时变路网下的求解方案与固定速度的静态路网下的求解方案进行对比。计算表2中各时段车速的平均速度作为车辆行驶的固定速度，并重新进行配送成本计算。通过计算可知各时段的平均速度为45.67 km/h。分别在固定速度下以及引入时变路网理论下对模型求解5次，其计算出的总配送成本对比如表6所示。

由表6可以看出时变模型的配送成本普遍要低于固定速度模型的配送成本。为了更加方便区分，将表6中数据绘制成折线图如图4所示。

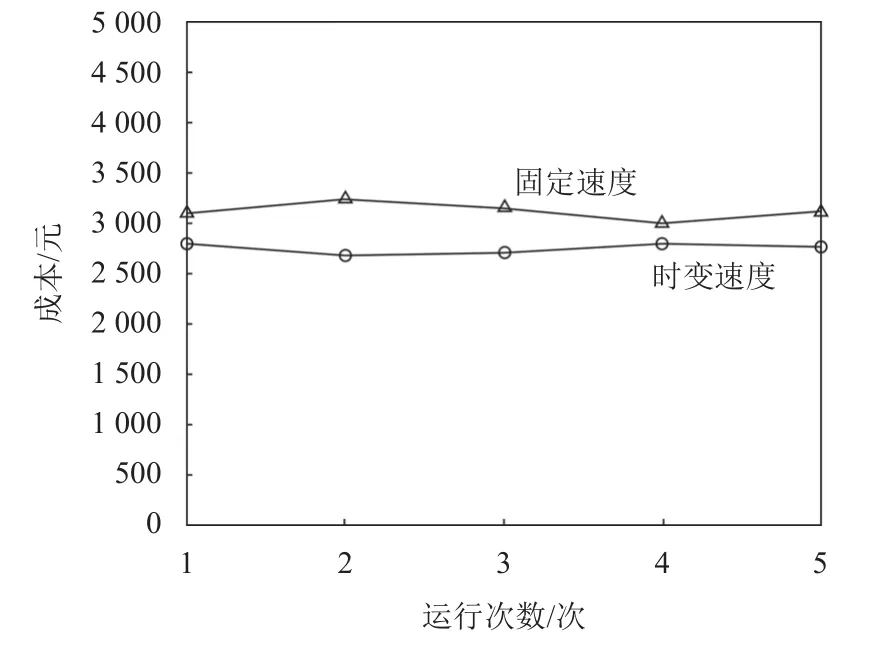
图4 配送成本对比图Figure 4 Comparison of distribution costs

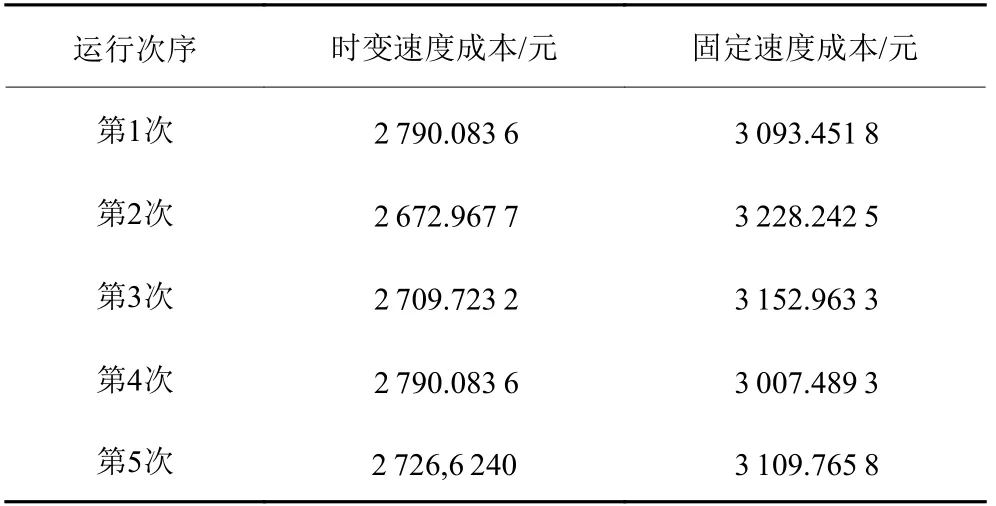
表6 不同速度配送总成本对比Table 6 Comparison of total delivery costs at different speeds

由图4及表6可知，在5次计算中，固定速度模型的配送总成本均在3 000元以上，平均值为3 118.382 5元；时变速度模型的配送成本均低于3 000元，平均值为2 737.896 4元。与固定速度相比，时变速度模型计算得到的平均配送成本降低12.201%，且更加符合实际情况，为企业压低预算，验证了模型的有效性。

计算结果在一定范围内波动是由于遗传算法进化过程的随机性引起的，且随着种群规模的扩大和迭代次数的增加，曲线的波动会越来越小，但计算时间也会相应地增加。由于本文种群规模设置为100，最大迭代次数设置为200，且通过图4可以看出两条曲线的波动范围不大，故本算法参数设置合理，计算结果可以接受。

4.4.2 不同规模对比

为了进一步验证模型的普适性，本文以配送中心为圆心，在半径40 km内随机生成不同规模的需求点分别运行模型，各时段车速依然选择表2中数据，除需求点的配送信息外其他参数均保持不变，计算结果如表7。

由表7可知，生成的10组对照数据中，在时变路网下的配送成本均低于传统静态路网下的配送成本。配送成本与需求点最终的聚类簇数有关，聚类簇数越多，则配送成本相对越高，这是由于聚类簇数反映了需求点的分布情况，簇数越多说明需求点分布较广，增加了车辆的行驶距离，也相应地增加了成本。通过这10组数据可以看出，在聚类簇数差别不大的情况下，需求点规模越大，基于时变路网规划出的配送路径所节约的配送成本越多。

表7 不同规模成本对比Table 7 Comparison of different scale costs

5 结论

本文研究时变路网下的电动冷藏车辆路径优化问题。首先，在传统的VRPTW模型的基础上，引入时变路网理论，设计与行驶时段相关的车速计算公式，并针对电动冷藏车电池容量小、充电频繁等短板，建立时变路网下考虑充电站的多时间窗约束的电动车辆路径优化模型；其次，运用AP聚类算法对配送区域进行划分以提高配送效率，并针对遗传算法的缺陷，设计改进的遗传算法对模型进行求解，以增强其寻优能力；最后，通过对比实验对模型的可行性进行验证。对固定速度下与时变速度下的配送成本进行对比分析，结果表明，与固定速度相比，时变速度下的配送方案可以使配送成本减少12.201%，为进一步验证模型的普适性，选取10组不同规模的案例进行验证，计算结果表明时变路网下的配送成本均低于静态路网下的配送成本。因此，本文基于交通的时变特性所建立的路径优化模型可以科学地规划配送路径，有效降低配送成本，对于企业配送方案的制定提供了决策支持，具有一定的现实意义。