随机需求下批发价格与支付时间相关的零售商最优库存策略研究

周永务，陈 怡，何 欢，陈传营

(1.华南理工大学 工商管理学院，广东 广州，510640；2.东莞理工学院 经济与管理学院，广东 东莞，523106)

在传统的经济订货批量模型中，供应商要求零售商在收到货物后立即支付货款。但在实际商业活动中，供应商为了激励下游零售商多订货，会给零售商提供价格折扣或者允许零售商延迟付款。在延迟付款期间内，零售商不需要支付资金占用成本和向供应商支付利息，并且可以通过销售产品来赚取利息。价格折扣策略使下游零售商支付较少的购买成本，增大订货量。延迟支付策略和价格折扣策略对企业库存策略的影响在供应链管理领域引起很多学者的关注与热烈讨论。

很多研究考虑供应商给零售商提供延迟支付策略，分析企业的库存决策。Jaggi等[1]考虑延期付款条件下易变质产品的EOQ模型。康凯等[2]考虑二级供应链下，分析碳限额对零售商和供应商库存策略的影响。此外，一些研究如Vandana等[3]、Feng等[4]考虑两级延期支付系统，即供应商允许零售商延期支付货款，零售商允许顾客延期支付货款，分析零售商的库存策略。Chen等[5]和张义刚等[6]考虑采用延迟支付策略来实现供应链协调。还有一些文献考虑市场需求是随机的情况，如Robb等[7]考虑需求和供应不确定下的贸易信贷模型；Gupta等[8]提出随机需求下的零售商的离散时间库存模型，证明零售商的最优策略结构不受贸易信贷的影响。

价格折扣作为供应商促销手段之一，虽然在一定程度上损害供应商的利润，但有助于增大零售商的订货量。部分研究考虑价格折扣策略下零售商的最优库存策略。Alan[9]发现当供应商提供临时价格折扣时，零售商可以考虑增加一个特殊订单来获得更多的效益。Sarker等[10]研究5种情况下零售商的最优订货策略，这5种情况分别是销售周期与补货周期一致、销售周期与补货周期不一致、销售周期比补货周期长、折扣价格是特殊订购数量的函数、增量折扣。Chang等[11]、Zhou等[12]考虑供应商给零售商提供一次性价格折扣时，提出针对易变质产品的零售商库存模型。成诚等[13]考虑供应商给零售商提供短期价格折扣，且允许零售商两次补货的库存模型，提出全局优化算法。

一些学者考虑供应商不仅给零售商提供贸易信贷策略，还提供价格折扣策略，来分析零售商的订货策略。李佐平等[14]考虑固定需求下供应商给零售商提供不同的延期支付期限和对应的价格折扣，分析零售商的订货策略。Feng等[15]考虑确定需求下，零售商为信用良好的客户提供贸易信贷，并要求信用不良的客户在收到商品后立即付款，供应商给零售商提供价格折扣和贸易信贷策略，零售商在约定时间内付款且提供价格折扣，研究零售商的最优订货周期和付款时间。Shah等[16]考虑当零售商的订货数量大于约定订货数量时，供应商为零售商提供现金折扣或贸易信用期的情形，分析零售商的订货策略和信用政策。一些库存策略研究文献考虑采用贸易信贷和价格折扣策略来实现供应链协调。Ho等[17]考虑供应商给零售商提供贸易信贷或者提前付款下的价格折扣，建立集成的供应商−零售商库存模型。Giri等[18]考虑价格敏感需求和两级贸易信贷政策下的单制造商−单零售商生产模型，其中制造商给零售商提供现金折扣和延迟付款策略，目标是集成系统的利润最大化。

综上，已有文献大都考虑需求确定场景下，供应商给零售商提供延迟支付策略或价格折扣策略，探讨零售商的库存决策。目前尚缺乏随机需求场景下，考虑与支付时间相关的批发价格下零售商的库存策略研究。而在商业场景中，为了吸引零售商尽早支付货款，供应商给零售商提供的批发价格可能是与零售商支付时间相关。并且随着市场竞争日益激烈，市场需求更容易受到需求随机波动的影响，零售商可能出现库存积压或库存短缺的现象，使零售商的成本增大。因此，本文假设供应商给零售商提供支付时间相关的价格折扣策略，并在模型中考虑随机需求这一因素，分析零售商的最优支付时间和目标库存决策，使零售商获得最大收益。本文假设当下游零售商延迟付款的时间越长，供应商提供的批发价格越高。通过分析零售商补货周期、支付时间和库存水平降为0的时间点的关系，确定零售商存在3种库存情形，并刻画每种情形下零售商的成本及收益，分析零售商的单位周期期望利润、最优目标库存以及支付时间。

1 符号说明和假设

本文考虑随机市场需求情形，供应商向零售商销售单一产品，零售商向市场销售这一产品。假设零售商的订货周期为常数，零售商在订货点向供应商订货，使零售商的库存水平达到目标库存。供应商允许零售商延迟支付全部货款，零售商的延迟支付时间不同，供应商给零售商制定不同的批发价格，但零售商的延迟支付时间不大于订货周期。零售商在延迟支付期内可以通过销售货物赚取利息，并且不需要支付资金占用成本。此外，本文假设零售商在支付时间点有足够的资金向供应商支付货款，提前支付不能获得折扣。在延迟支付期内，零售商利用销售收入赚取收益，并且不需要向供应商支付利息。与文献[6]一致，假设补货提前期为常数，本文不失一般化设为0。本文假定允许缺货，零售商采取缺货不补策略，不考虑缺货成本。为了方便说明，设*表示最优值，金额都以“元”为单位。

本文的符号说明如下：

D为月市场需求，随机变量；

p为单位产品的销售价格；

T为零售商的补货周期(月)，常数；

Y为零售商补货的目标库存，决策变量；

Q为零售商的订货量；

tp为零售商的延迟支付时间(月)，决策变量；

ω(tp)为供应商给零售商提供的批发价格，其中，ω(tp)=ω0+αtp，ω0为 基础批发价格，α为变化参数，ω0和 α 都为常数；

Ie为单位资金的月利息收入；

Ic为单位资金的月利息支出；

h为单位产品的月库存成本，不包含利息支出；tz为零售商库存水平降为0的时间(月)；

I(t)为零售商在t时刻的库存水平；

R(E)为零售商的期望单位周期收益。

CP为购买成本；

RS为销售收入；

CH为库存成本(不包含利息支出)；IC为利息支出成本；

IE为利息收入；

RE为零售商的单位周期收益。

2 模型构建

本文假设市场需求D是随机的，则dI(t)/dt=−D。 考虑边界条件I(0)=Y，I(tz)=0 ，得I(t)=Y−Dt，且Y=Dtz，因此零售商的订货量为Q=Y−I(T)。在随机市场需求条件下，零售商库存水平降为0的时间点tz也是随机的[19]。考虑零售商的支付时间tp、补货点T以及库存水平降为0的时间点tz，存在3种库存情形，分别是tz≤tp≤T，tp≤tz≤T，tp≤T≤tz。

2.1 情形1：tz≤tp≤T

如图1，在情形1下，零售商的库存水平在向供应商支付货款前降为0，则零售商的订货量与目标库存相等，即Y=Q，且利息支出成本为0。零售商可以在时间0到支付时间点tp期间赚取利息收入，需要在时间0到库存水平降为0期间支付库存成本(不包含利息支出)。零售商单位周期的收益和成本如下。

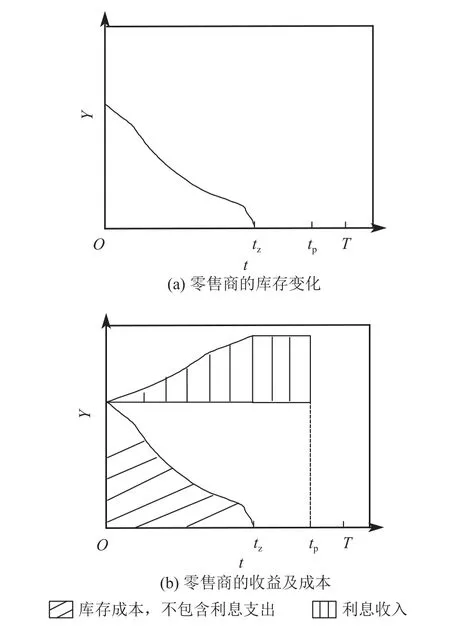
图1 情形1：零售商的库存变化、收益及成本Figure 1 Scenario 1: Inventory change, benefits, and costs of the retailer

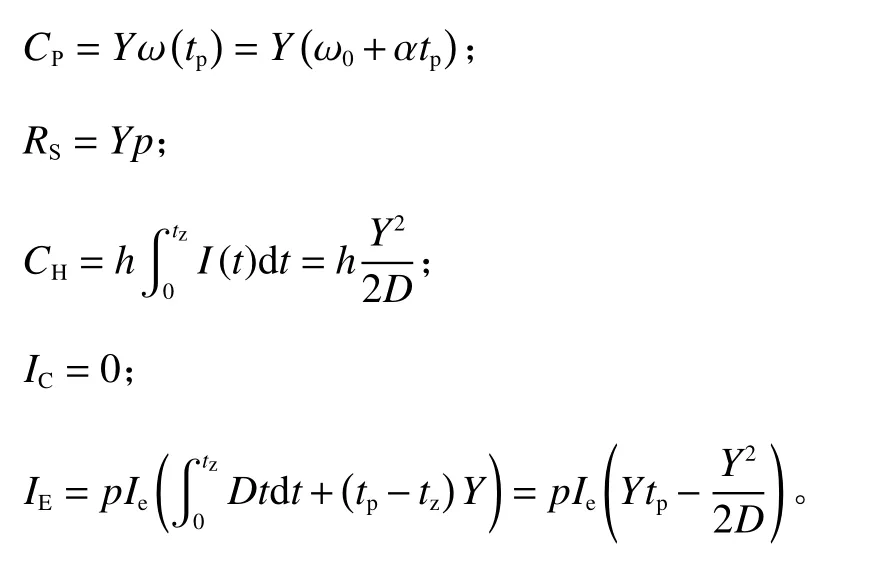
情形1下，零售商的单位周期收益为

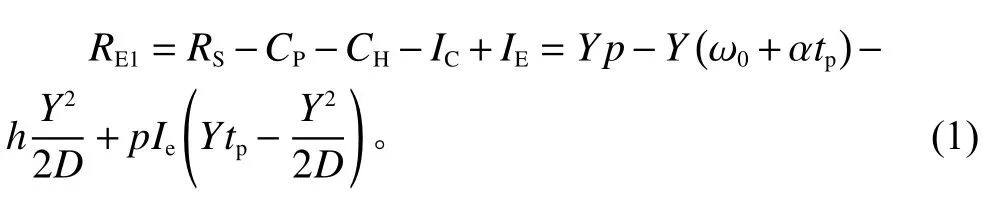
2.2 情形2：tp≤tz≤T

如图2，在情形2下，零售商的库存水平在向供应商支付货款后降为0，则在支付时间点tp到库存水平降为0的时间点tz期间，零售商需要支付利息支出成本。零售商在时间0到支付时间点tp期间可以通过销售产品赚取利息收入，需要在时间0到库存水平降为0期间支付库存成本(不包含利息支出)。因为零售商的库存水平在订货点T前降为0，零售商的订货量为Q=Y。零售商单位周期的收益和成本如下。

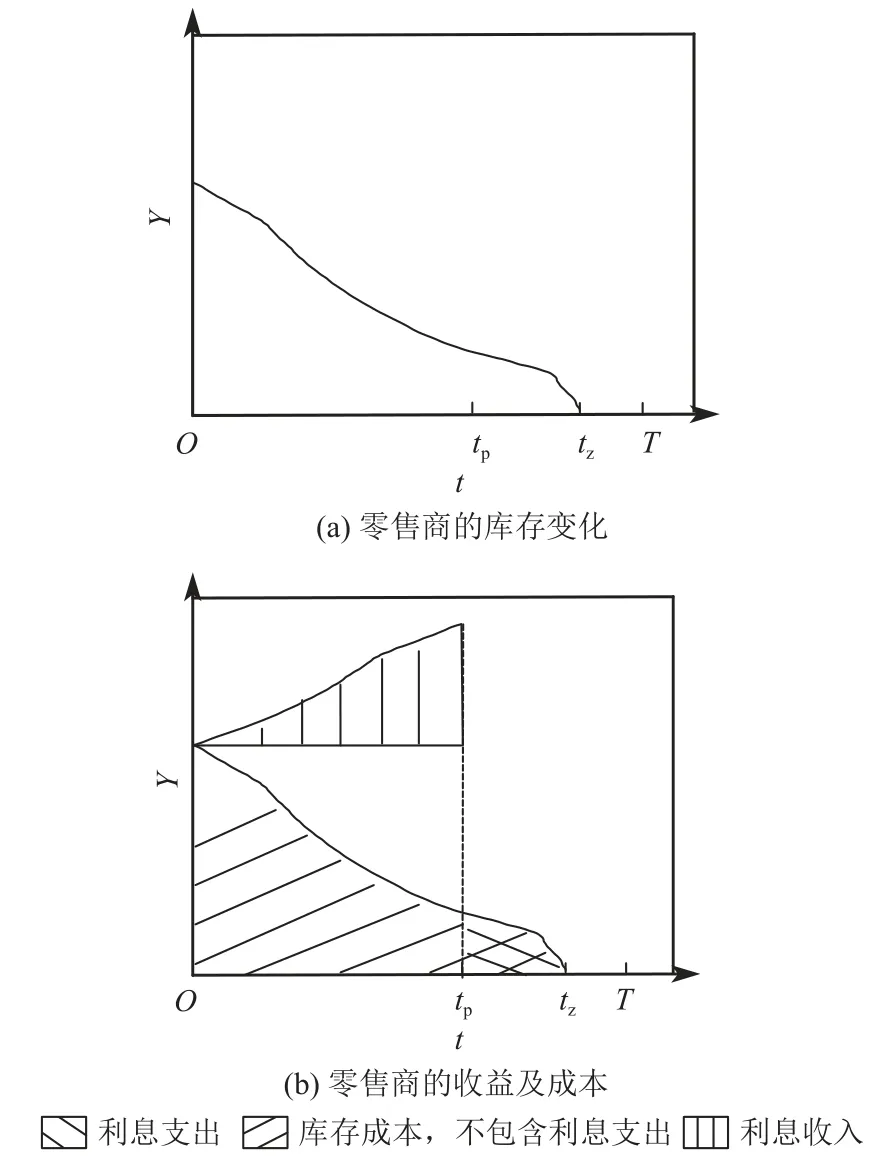
图2 情形2：零售商的库存变化、收益及成本Figure 2 Scenario 2: Inventory change, benefits, and costs of the retailer

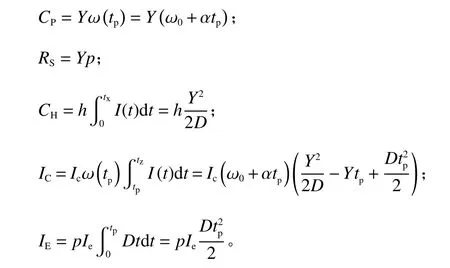
在情形2下，零售商的单位周期收益为

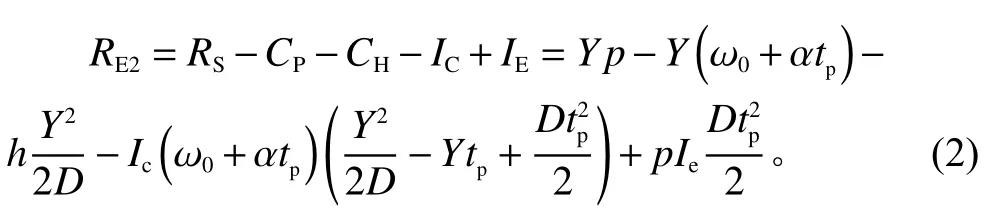
2.3 情形3: tp≤T≤tz

如图3，情形3下，销售周期结束时，零售商还存在库存，订货量和销售周期销售量为Q=Y−I(T)=DT。在零售商向供应商支付货款后，库存水平未降为0，需要在支付时间点tp到 订货点T期间支付利息支出。零售商可以在未支付货款的期间通过销售货物赚取利息收入，但需要在时间0到库存水平降为0期间支付库存成本(不包含利息支出)。零售商单位周期的收益和成本如下。

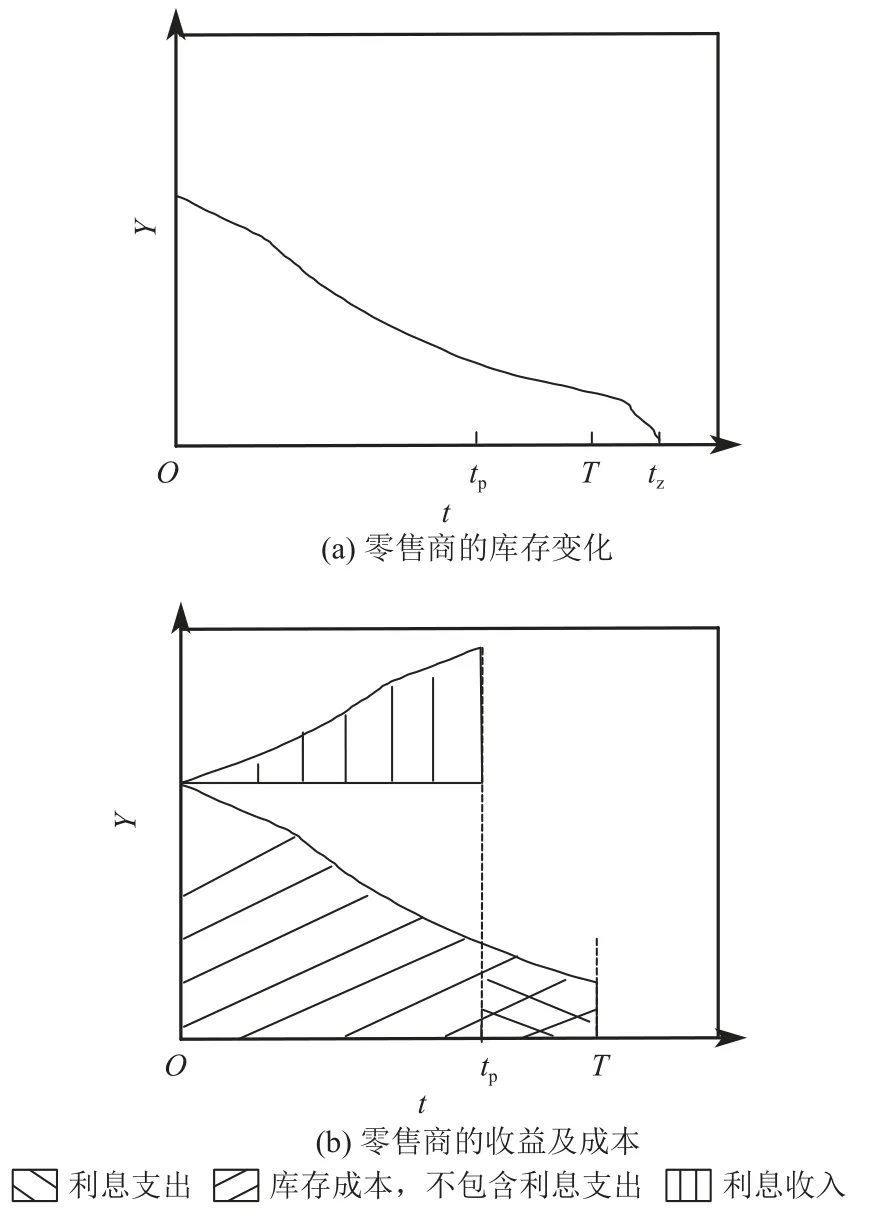
图3 情形3：零售商的库存变化、收益及成本Figure 3 Scenario 3: Inventory change, benefits, and costs of the retailer

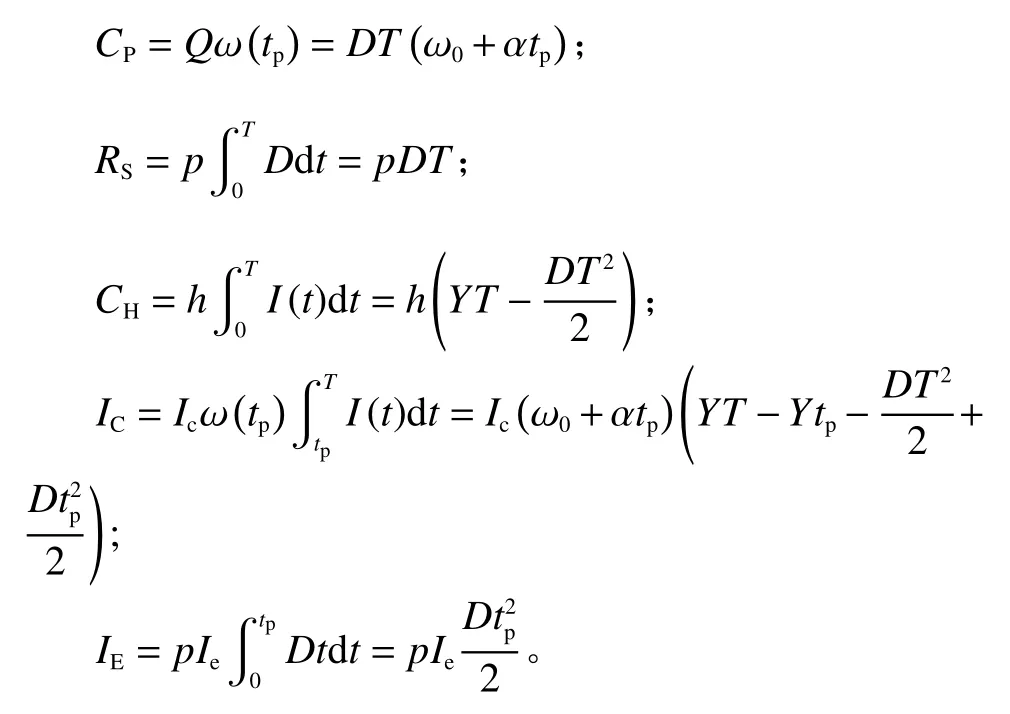
情形3下，零售商的单位周期收益为

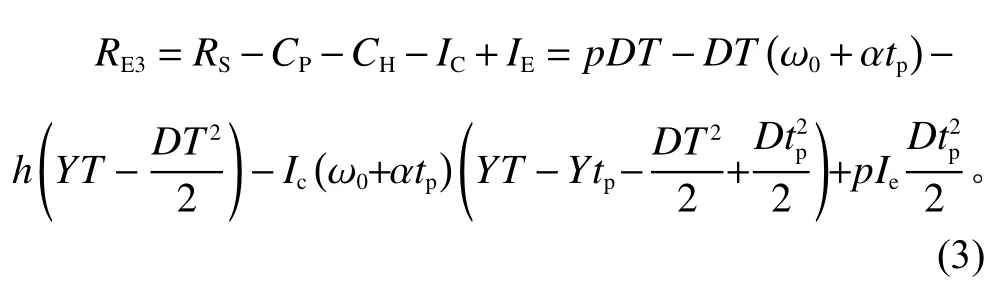
3 收益分析

考虑3种情形，零售商的期望单位周期收益为

求RE关于Ie和p的一阶导数，可得性质1。

性质1RE随着Ie、p的增大而增大。

当零售商单位资金的月利息收入Ie增大时，零售商可以从销售的货物中获得更多的利息收入，因此零售商的期望单位周期收益更大。当零售商的销售价格p增大时，零售商可以获得更多的销售收入和利息收入，零售商的期望单位周期收益增加。

求RE关于h、α 、ω0和Ic的 一阶导数，可得性质2。

性质2RE随h、α、ω0、Ic的 增大而减小。

当零售商的单位产品的月库存成本增加时，零售商需要付出更多的库存成本。当供应商提供的基础批发价格增大时，零售商需要付出更多的购买成本、库存成本和利息支出成本，导致零售商的期望单位周期收益减小。当批发价格的变化参数增大时，延迟支付时间的增大会使批发价格增大的幅度更大，零售商的期望单位周期收益减小。当零售商的单位资金的月利息支出增大时，零售商需要付出更多的利息支出成本，使期望单位周期收益减小。

3.1 考虑延迟支付时间外生

考虑零售商延迟支付时间tp外生的情形，对零售商的期望单位周期收益RE求 关于目标库存Y的一阶、二阶导数，有

式(6)中，RE是关于Y的凹函数。令∂RE/∂Y=0，得到

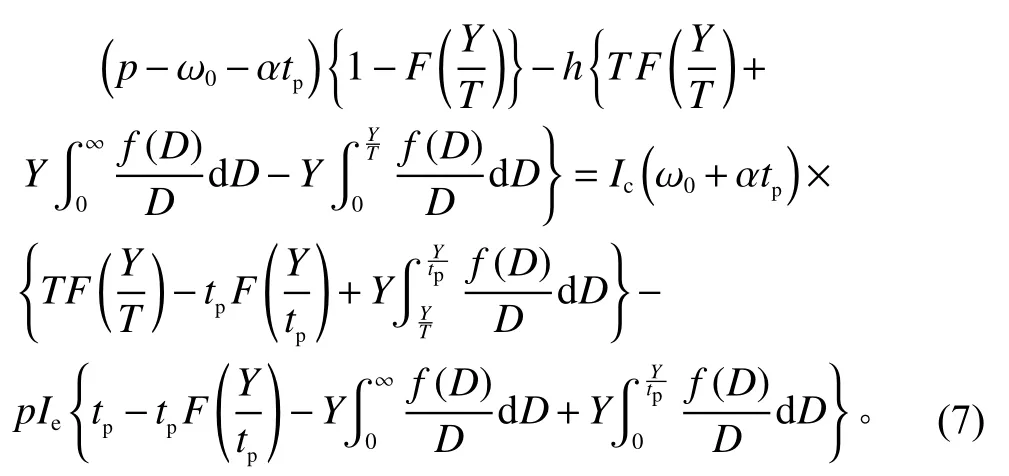
式(7)两边分别对Y求一阶导数，有

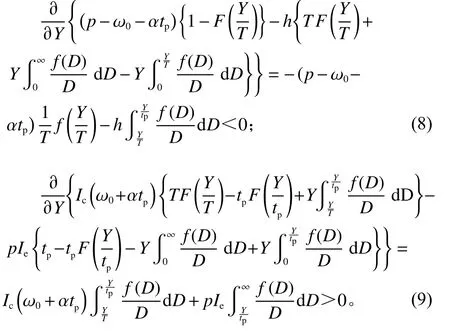
由式(8)、(9)可得，RE存 在唯一的最优解Y*，可得到性质3。

性质3RE是 关于Y的凹函数，且RE存在唯一的最优值Y*，最优值满足∂RE/∂Y=0。

3.2 考虑延迟支付时间内生

考虑零售商延迟支付时间tp内生的情形，存在

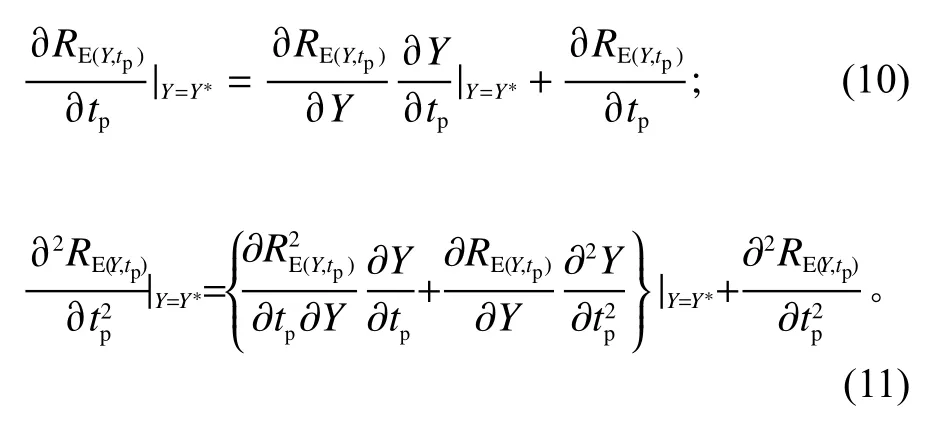
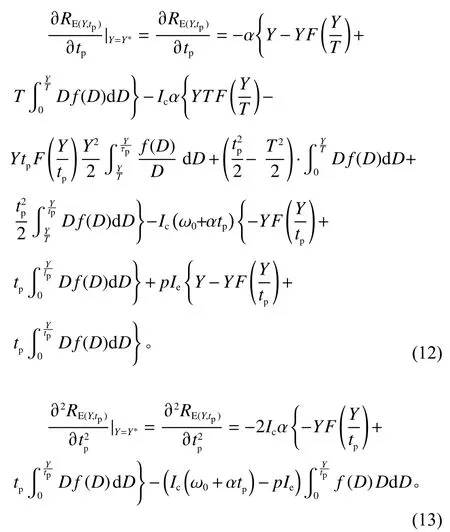
性质4若，则RE是 关于tp的凹函数，且tp最 优值满足∂RE/∂tp=0。

性质4表明，若上游供应商提供给下游零售商的批发价格变化范围较小，即变化参数α 较小，条件能得到满足，零售商可以确定最优的延迟支付时间来获得最大期望单位周期收益，最优延迟支付时间满足∂RE/∂tp=0。

3.3 特殊例子：考虑 I e=0，Ic=0

假设零售商的资金成本(包含利息收入和利息支出)是可以忽略的，即Ie=0，Ic=0，这时零售商的期望单位周期收益为

求R′E 关于tp的 一阶导数，有∂R′E/∂tp＜0，则零售商的期望单位周期收益RE′随零售商延迟支付时间tp的 增大而减小，有。当Ie=0，Ic=0，由式(6)，可得。 因此，RE′是关于Y的凹函数，最优值满足，则可得性质5。

性质5当忽略零售商的单位资金的月利息收入和月利息支出，零售商选择在订货点支付货款；零售商的最优目标库存Y*满 足∂RE′/∂Y=0。

当下游零售商的单位资金的月利息收入和月利息支出很小时，零售商延迟支付货款带来的利息收入对总收益影响很小，但延迟支付货款使零售商付出较大的购买成本，因此零售商会选择在订货点支付货款来获得最大的期望单位周期收益。

4 数值例子和敏感性分析

假设市场需求D服从正态分布，记为D∼N(µ,σ2)。其中，µ为市场需求均值； σ为市场需求标准差。参照Shah等[16]的数值例子，本文的数值例子为：Ic=3%，Ie=1%，h=2，p=60，ω0=40，α=1，µ =800，σ =100，T=8。 在该例子中，零售商的最优目标库存为Y*=4 851.96 ，最优支付时间tp*=2.02 月，期望单位周期收入为49 621.9元。

图4刻画各参数变化对Y*、t*p、R*E的影响。由图4(a)，当市场需求的标准差增大时，零售商的最优延迟支付时间和最优目标库存会减小，并且期望单位周期收益也减小。这是当市场需求波动增加时，零售商趋向于缩小延迟支付时间来获得较小的批发价格，并减小目标库存来降低可能由市场需求减小带来的库存成本(不包含利息支出)和利息支出，即零售商是倾向于避免市场需求波动带来更大的损失。因此，考虑采取适当的措施控制市场需求的波动能有效保障零售商的收益。在高晓敏等[20]的数值例子中，市场需求波动的增加使零售商增大订货量，而在本文中，市场需求波动的增加使零售商减小目标库存，这表明延迟支付政策和价格折扣政策会改变零售商的订货偏好(见图5)。另外，零售商的最优延迟支付时间、最优目标库存和期望单位周期收益关于单位产品的月库存成本(不包含利息支出)、批发价格的变化参数的变化趋势与关于市场需求标准差的变化趋势类似。这是因为单位产品的月库存成本(不包含利息支出)或批发价格的变化参数增加时，零售商需要支出更大的成本(库存成本、购买成本)，零售商倾向于减小目标库存和缩短延迟支付时间来控制成本。

图4 参数变化对 Y* 、t p*、R*E的影响Fig ure 4 The effect of parameters change on Y* 、、

图5 与其他文献的对比实验：考虑市场需求标准差变化Figure 5 Comparative experiment with other paper: consider the change of market demand standard deviation

由图4(b)，当市场需求均值增加时，零售商会选择增大目标库存和延迟支付时间，并且能获得更大的期望单位周期收益。市场需求均值增加会使销售周期总需求增加，零售商需要更多的库存来应对市场的需求，此时增大延迟支付时间能较大控制利息支出，并且获得更多的利息收益，继而增大期望单位周期收益。在Shah等[16]的数值例子中，零售商收益变化的比例与市场需求变化的比例几乎一致，而在本文考虑随机需求的情况下，零售商通过调整目标库存和支付时间获得的收益增大比例更大。这说明本文提出的模型不仅考虑实际中需求波动的风险，还能够为零售商在需求增大时带来更大的收益提升(见图6)。另外，零售商的最优延迟支付时间、最优目标库存和期望单位周期收益关于销售价格、单位资金的月利息收入的变化趋势与关于市场需求均值的变化趋势类似。这是因为销售价格或单位资金的月利息收入增加时，零售商增大目标库存和延迟支付时间可以获得更大的收入(销售收入、利息收入)，继而获得更多的期望单位周期收益。

图6 与其他文献的对比实验：考虑市场需求均值变化Figure 6 Comparative experiment with other paper: consider the change of average market demand

由图4(c)可知，当供应商提供的基础批发价格逐渐增大时，零售商的最优延迟支付时间先增大后减小，这是因为当基础批发价格增大一定幅度时，零售商增大延迟支付时间能有效控制资金占用成本，而当基础批发价格增大幅度较大会导致零售商的购买成本增加较大，利润空间压缩，零售商选择减小延迟支付时间控制购买成本。另外，基础批发价格增大会使零售商降低目标库存以控制资金占用成本。最后，基础批发价格增大使零售商的期望单位周期收益减小。因此，零售商应与供应商协商获得较低的基础批发价格来保障收益。

由图4(d)可见，当单位资金的月利息支出增加时，零售商会选择增加延迟支付时间、减小目标库存。这是因为零售商延迟支付时间增加时，能有效控制单位资金的月利息支出增加带来的单位产品利息支出增加；为了控制总的利息支出，减小目标库存也是零售商的有效措施。很显然，单位资金的月利息支出增加会使零售商的期望单位周期收益减小。因此，零售商应该关注自身单位资金的月利息支出，采取合适的融资措施降低资金成本。

5 结论

本文考虑随机市场需求下，供应商给零售商提供支付时间相关的批发价格，研究零售商库存和支付时间模型，探讨随机需求、延迟支付策略和价格折扣策略对零售商目标库存和支付时间的影响。结果表明，零售商的期望单位周期收益是关于目标库存的凹函数，且存在唯一的最优目标库存。当供应商向零售商提供的批发价格变化参数较小时，零售商的期望单位周期收益是关于支付时间的凹函数。当零售商的单位资金的月利息收入、月利息支出可以忽略时，零售商选择在订货点支付货款。此外，市场需求波动增大时，零售商的最优支付时间和目标库存减小，以控制需求波动对期望单位周期收益的影响；市场需求均值增大时，零售商的最优支付时间和目标库存增大，并获得更大的期望单位周期收益。