基于最小偏向角法的高精度液体折射率测量装置的优化设计与测量研究

付兴丽，冯 杰，范晓辉，潘梦芸，韦秋叶

（1. 广西工业职业技术学院, 广西 南宁 530001；2. 广西壮族自治区计量检测研究院, 广西 南宁 530200）

1 引 言

折射率是物质的一种基本物理属性，它反映了物质中微观粒子的性质和数量，对物质性质的研究具有重要的指导意义。例如，在对于光学材料的研究中，折射率是光学薄膜[1]、光学玻璃[2]、光学棱镜[3]等材料的关键指标；在纳米材料研究中，纳米样品的折射率是激光粒度测量[4]、表面缺陷研究[5]的重要影响因素。由此可见，折射率的准确测量对物质性质表征至关重要。在折射率测量中，液体介质由于易受到流体性质、温度、溶液组分等因素的影响，要实现高精度测量并不容易。而液体折射率的测量被广泛应用于食品、石化、医药、化工等诸多领域，特别是涉及糖、酒精、食品添加剂含量的测定时，往往需要精准测定液体产品的折射率以进行表征[6]。所以，高精度的液体折射率测量方法和仪器受到了大家的关注。

液体折射率测量按原理可分为几何光学和波动光学两类。其中，波动光学方法可达到较高的测量精度[6]，日本国家计量院[7]采用激光干涉法测量液体折射率，能实现10-6级别的测量不确定度，Wu 等[8]采用光学频梳法测量空气折射率获得10-8级别的测量不确定度，Meng 等[9]利用迈克尔逊干涉仪，采用激光锁模方法测量水的折射率，不确定度达到10-5。但上述高精度的液体折射率测量存在装置结构复杂、设备成本高、实验条件苛刻等缺点，不适用于常规研究的折射率测量。

目前应用最广泛的液体折射率测量是几何光学原理的方法，以全反射临界角法的阿贝折射仪最为普遍。阿贝折射仪结构简单、易于操作，但测量精度一般只能达到10-4，不能满足高精度测量要求。另一种采用最小偏向角法的折射率测定仪，具有更高的测量精度[10-11]，并且能直接溯源至角度基准，不需要依赖折射率标准参考物，是国际计量委员会认可的基准测量方法。但该方法对测试样品有特殊角度要求，测量无固定角的流体介质时会遇到困难。孙一书等[12]采用金属框架配合等厚玻璃窗口制成三角棱体液体盛装器皿，应用于最小偏向角法测角仪测量液体折射率，获得了10-6测量不确定度，但该器皿只对光程和角度进行了精准加工和误差计算，并没有精确控温，也未定量评价温度对液体折射率的影响。而温度是液体折射率的最大影响因素，因此限制了其在高精度液体折射率测量中的应用。

本文设计了一种全新的恒温空心三棱镜装置，通过恒温管路设计实现了待测液体精准控温，具备优异的角度精度和良好的光学透过率，使待测液体可在低波动、均匀温场条件下实现最小偏向角法的折射率测量，为高精度液体折射率测量提供了新的解决方案。

2 测量原理

最小偏向角法测量折射率原理如图1 所示，光束从折射率为n0的介质入射到折射率为nx的三棱镜的一侧，经折射后从棱镜另一侧出射。当图中α1=α2，β1=β2时，偏向角D为最小。

图1 最小偏向角法原理图Fig. 1 Principle of minimum deviation angle method

此时，各角度关系如下：α1=α2=(A+D)/2,β1=β2=A/2。根据折射定律，待测棱镜的折射率nx为：

由式（1）可知，待测折射率是顶角A和最小偏向角D的函数，只要测量最小偏向角D即可求得待测物的折射率nx。

3 恒温空心三棱镜装置的设计

最小偏向角法是目前国际上应用最成熟的高准确度液体折射率测量方法，它可溯源到角度基准，但通常只能应用于三棱柱形状固体材料的折射率测量。为将最小偏向角法应用于液体折射率测量，需要研制精确且已知顶角的空心三棱镜，通过精确控温，测量特定温度下的液体折射率。研制了一种新型的带水浴控温的空心三棱镜装置，包括测量池、恒温夹套、温度传感器和控制器等部件（如图2 所示）。

图2 恒温夹套和空心三棱镜实物图Fig. 2 Physical pictures of thermostatic jacket and hollow prism

恒温空心三棱镜装置的立体示意图如图3 所示。测量池和恒温夹套均为空心等腰三棱柱体，等腰三棱柱的顶角设计为55°。测量池嵌套在恒温夹套内，用于盛装待测液体样品。恒温夹套的至少两个侧面上设置有观测窗，使光线通过一个观测窗照射进测量池内的待测液体样品，从另一个观测窗折射出去，控制器根据光线在观测窗的入射角度和出射角度通过测角法获得待测液体样本的折射率，恒温夹套外壁和内壁之间铺设有空心管路，用于连接循环水浴，温度传感器用于测量恒温夹套和测量池的温度，控制器通过温度传感器测量的温度控制循环水浴中的水在空心管路中的循环，从而控制测量池的温度恒定。

图3 恒温空心三棱镜装置立体示意图Fig. 3 The stereoscopic model of thermostatic hollow prism

为了提高装置的温度交换性能，降低各个区域的温场差异，恒温夹套和测量池均设置成包括顶盖和筒体的可拆接形式。在测量池和恒温夹套的顶盖上均设置多个通孔，用于插入不同的测温探头，以测量不同区域的温度。此外，恒温夹套内设置有逆流式布置的空心管路，空心管路距离夹套内、外壁的间距相等，并且不同管路也呈间距相等的均匀迂回分布（如图4 所示）。测量池采用熔融石英材质制成，恒温夹套采用高导热性金属材料制成。夹套采用金属材料既可以更快、更均匀地进行热交换，金属也更容易进行精确加工，以达到完全贴合测量池的角度与平整度。最后，测量池和恒温夹套之间还填充有导热硅脂。通过恒温夹套空心管路的水路设计，进一步减小因循环水浴的温度波动而带来的被测液体温度波动，同时通过改善液体不同区域的温场均匀性，以提高折射率测量精度。

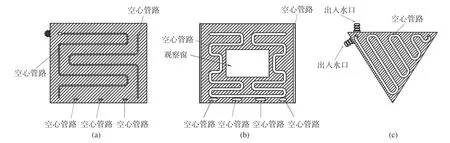
图4 恒温夹套平面示意图。（a）无测量窗的侧面；（b）有测量窗的侧面；（c）顶面和底面Fig. 4 The planar graph of thermostatic inner layer. (a) Side without measuring window; (b) side with measuring window;(c) top and bottom

为了保证测量光线能完全通过恒温空心三棱镜装置，做了如下优化设计：（1）恒温夹套的顶角与测量池的顶角相等，均为55°，角度误差不超过±0.1°。（2）夹套观测窗采用由外向内形成45°角的梯台开孔形式，可以在入射和出射光线与观测窗之间夹角不大于45°时，仍能保证光线不被遮挡。（3）测量池采用在200～1 000 nm光谱透过率高于80% 且无明显特征吸收的熔融石英材质。（4）测量池经过精密加工，保证其光学平面具有优异的垂直度、内外平行度、光洁度，测量池光学平面检测结果如图5 所示。

图5 测量池三棱镜器皿加工测试数据Fig. 5 Processing test data of prism vessels in measuring cell

4 液体折射率测量实验与结果

4.1 实验步骤

最小偏向角法测量液体折射率实验采用的是德国Trioptics SpectroMaster®高精度手动折射率测量仪。图6 为测量装置图。此仪器由中国计量科学研究院计量校准做比对测试，测角误差为0.5″，测试数据准确可信。测量波长为钠光特征波长589.3 nm，波长准确性小于0.1 nm，光源采用具有相应光谱的光谱灯通过窄带滤光片进行筛选。

图6 高精度手动折射率测量仪Fig. 6 High precision manual refractive index measuring instrument

待测样品为水、异辛烷、四氯乙烯3 种纯液体，按照以下步骤对样品进行折射率测量：

（1）测试实验室为恒温实验室，环境温度控制在目标温度±1 °C 以内，样品测试前至少恒温12 h。

（2）恒温空心三棱镜装置被置于样品承载台上，将待测液体样品注入测量池，将测量池、恒温夹套、外部循环水浴按图3 所示连接好。

（3）打开循环水浴，将测温探头插入测量池，通过监测测温探头反馈的实际温度值，调整恒温循环水浴的设置温度，待样品的温度达到目标温度（±0.03 °C）且稳定时可进行液体折射率测量。

（4）打开高精度手动折射率测量仪进行预热，选择顶角测量程序，按照仪器操作程序测量三棱体的顶角A。

（5）调节目镜位置，找到由三棱镜折射的光谱线，按照仪器操作程序测出最小偏向角D。

（6）测量角度的同时实时监测样品温度，保证在测量时待测样品温度在目标温度±0.03 °C 范围内；同时记录测量时的环境温度、湿度、大气压强等数据，由Edlen 公式[13]计算空气折射率。

（7）由仪器自动根据测量程序计算出折射率测量值。重复上述步骤测量6 次，得到多组折射率重复测量数据。

4.2 仪器与试剂

实验中使用的其它主要仪器、装置的型号及生产厂家列于表1。

表1 实验仪器Tab.1 Experimental instruments

实验中使用的主要试剂及生产厂家列于表2。

表2 实验试剂Tab.2 Experimental reagent

4.3 测量结果

4.3.1 不同温度下的液体折射率测量

分别设定目标测量温度为15，20，25 °C，环境温度控制在目标温度±1 °C 内，待测样品温度控制在目标温度±0.03 °C 范围内。在不同温度下所测得的液体折射率量值如表3 所示。

表3 液体折射率的实验数据与统计学分析Tab.3 Experimental data and statistical analysis of liquid refractive index

从表3 可知，在15～25 °C 范围内，对于3 种待测液体，最小偏向角法的测量折射率能达到10-7的精度。由于使用了恒温装置控温，使测量在非常恒定的条件下进行，因此测量重复性也达到10-6至10-7水平。

4.3.2 两种不同原理的的液体折射率测量

为了验证最小偏向角法测量液体折射率的准确性，使用全反射角法原理的高精度台式液体折射仪在20 °C 下对待测液体进行复测，每种液体测量6 次，每种液体测量前均用德国联邦物理技术研究院Physikalisch-Technische Bundesanstalt（PTB）研制的液体折射率标准物质（证书号：2380PTB 19、1659 PTB 14、1890 PTB 16）对仪器进行校准修正，使其测量值具有溯源性。两种不同原理的比较测量结果列于表4。

从表4 可知，在20 °C 下，两种不同原理的液体折射率测量偏差小于2×10-6。由于阿贝折射仪测量值溯源到PTB 标准物质，由此验证了最小偏向角法测量值也具有很高的准确性。

表4 两种不同原理的测量结果Tab.4 Comparative results of two different principles

4.3.3 环境温度下的液体折射率测量

为了验证精确控温对液体折射率测量的重要性，在环境温度为20 °C 时，将恒温循环水浴关闭，此时空心三棱镜装置未处于水浴控温状态，待测液体温度随环境温度波动而变化，即：(20±1) °C。在此条件下测得液体折射率如表5所示。

表5 环境温度下的液体折射率Tab.5 Refractive indices of liquid at ambient temperature

将3 种待测液体在(20±1) °C 的环境温度下的折射率进行线性拟合，计算的折射率变化系数达到-6×10-4/°C，远远达不到高精度测量的要求。由此，说明了通过恒温三棱镜进行精确控温的重要性。

5 测量不确定度分析

由公式（1）得知，待测液体的折射率nx主要受到空气折射率n0，顶角A和最小偏向角D的影响，此外还受到温度测量的影响。根据各项实验参数和测角数据，分别计算了3 种待测液体的折射率不确定度。

5.1 空气折射率的影响

空气折射率与环境温度、湿度、压强有关，计算公式为Edlen 公式[13]，试验过程中，压强波动范围为：1 007.61～1 022.72 hPa，温度波动范围为：19～25.6 °C，湿度变化范围为：34%～73%RH，经过计算，试验过程中空气折射率变化范围为：1.000 268 029～1.000 273 377。取均匀分布，空气折射率的不确定度为：u(n0)=(1.000 273 377-1.000 268 029)/=3.46×10-6。由此计算空气折射率对待测液体折射率引入的不确定度u1如表6 所示。

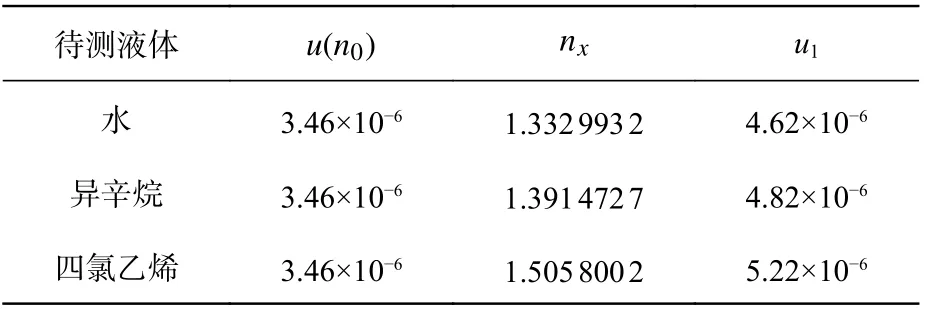
表6 空气折射率引入的标准不确定度分量Tab.6 Standard uncertainty introduced by air refractive index

5.2 温度的影响

由PTB 发布的折射率标准物质证书[14]得知，液体折射率与温度之间存在以下关系：nx=n(20)+a×(t-20)+b×(t-20)2。则影响折射率的温度系数ct为：ct==a+b×(t-20)。温度波动 Δt取均匀分布，则温度引入的不确定度为：u2=ct×Δt/。实验中，通过手持式参考测温仪持续监测空心三棱镜内液体的温度波动（温度设定在20.00 °C），最大的温度波动 Δt=0.03 °C。在（20±1） °C 范围内对每一种液体做了nx-t工作曲线，计算得到各液体的测温常数a,b值，最后计算测温误差引入的不确定度u2列于表7。

表7 测温误差引入的标准不确定度Tab.7 Standard uncertainty introduced by temperature measurement error

5.3 测角误差的影响

由仪器证书可知，高精度手动折射率测量仪角度测量精度为±0.5”，取均匀分布，则角度测量的标准不确定度为：

3 种待测液体折射率测量的角度数据列于表8。

表8 顶角及最小偏向角实验数据Tab.8 Experimental data of vertex angle and minimum deviation angle

测角误差引入的不确定度：

由公式（1）分别计算得3 种液体的顶角A和最小偏向角D的灵敏系数，最后得到测角误差引入的不确定度u3如表9 所示。

表9 角度测量误差引入的标准不确定度分量Tab.9 Standard uncertainty introduced by angle measurement error

5.4 合成不确定度

由重复性、空气折射率、温度、测角误差引入的4 个不确定度分量分别合成3 种液体折射率测量不确定度，计算公式为：

其中重复性引入的不确定度分量为us=s/。各不确定度分量及合成不确定度列于表10。

表10 不确定度分量及合成不确定度Tab.10 Uncertainty component and combined uncertainty

6 结 论

本文设计的恒温空心三棱镜装置，应用于最小偏向角法测量液体折射率，实现了液体控温，精度达到(20±0.03) °C，测量折射率范围在1.333 0～1.505 8 的3 种液体，测量精度和重复性均达到10-7水平，测量不确定度最大为1.3×10-5。通过实验发现，对于有机液体而言，温度是液体折射率最重要的影响因素，0.03 °C 的温度波动对20 °C 下折射率的测量不确定度贡献达70%。因此，使用优化设计的恒温空心三棱镜装置，能为最小偏向角法的液体折射率测量提供精准的控温和角度测量条件，解决了高精度液体折射率测试问题。