基于视觉显著性加权与梯度奇异值最大的红外与可见光图像融合
程博阳,李 婷,王喻林
(中国空间技术研究院遥感卫星总体部, 北京 100094)
1 引 言
红外与可见光图像融合是目前应用最为广泛、也是最具有研究价值的图像融合方式。可见光图像是反射类图像,高频成分多,在一定照度下能反映场景的细节[1]。红外图像则是热辐射图像,灰度值由目标与背景的温差决定,但不能反映真实的场景[2]。将上述两种图像相融合,可将其光谱信息保留并结合到一起,有利于增强图像系统对场景的表达能力,在视觉感知、军事应用、电子产品检测、遥感资源探测等众多领域中都有广泛的实用价值[3]。
近年来,由于多尺度分解(Multi-Scale Transform,MST)[4]方法具备良好的视觉感知效果,因此被逐渐应用到红外与可见光图像融合方法中。MST 融合方法并不直接处理图像的像素元,而是以图像滤波器作为辅助手段,通过多级别的滤波处理获取不同分辨率、不同尺度的子带分量图像[5]。其中,近似层分量表现了图像的主体与能量特征,而细节层分量则凸显图像的边缘细节与梯度特征[6]。通过寻求符合两类分量本质的融合规则,则可获取具有较好视觉效果的融合图像[7]。目前常用的MST 工具主要有离散小波变换(Discrete Wavelet Transform, DWT)[8],曲波变换(Curvelet Transform,CT)[9],非下采样轮廓波变换(Nonsubsampled Contourlet Transform, NSCT)[10],非下采样剪切波变换(Non-subsampled Shearlet Transform, NSST)[11]等。其中DWT 的基函数通常被限制在正方形区域内,导致其对图像边缘的捕捉和还原能力不强,融合后的图像非常容易出现块状效应。虽然CT 的基函数在捕获图像边缘与直线奇异性等方面比DWT 的基函数更快,但无法消除伪吉布斯现象。NSCT 与NSST 均采用非下采样塔式滤波器(Non-Subsampled Pyramid,NSP)作为尺度分解工具,在增加平移不变性的同时还消除了伪吉布斯现象。但相比于NSCT,NSST 其特有的“剪切波梯形基函数”可对图像的边缘曲线进行更为贴近的拟合,因此它具备稀疏特性、多方向性,非常适合于高维图像信息的多方向处理[12]。然而NSST 仍存在遗漏图像边缘细节信息的缺陷,主要是由于NSP 对细节的捕捉能力较差,在图像进行多尺度分解后,其高频分量会丢失纹理梯度特征。因此为了获得更为精细的多尺度分解效果,还需寻找更为先进的多尺度滤波器来代替NSP,将其组成为全新的塔式多尺度分解工具。
边缘保持滤波算法成功地应用于图像的多尺度表示中,在时域内采用边缘保持滤波器对图像进行迭代滤波,得到近似图像,将源图像与滤波输出图像进行差分运算得到细节图像,利用方向滤波器组对细节图像进行方向分析,实现图像的多尺度、多方向分解[13]。在众多边缘保留滤波器中,滚动引导滤波器(Rolling Guidance Filter,RGF)[14]不仅可以平滑图像纹理信息,同时在实现过程中利用迭代来保留图像的边缘信息,因此可以有效地应用到多尺度图像处理中。基于上述描述,可采用RGF 构成全新的多尺度滚动引导滤波器(Multi-scale Rolling Guidance Filter, MS-RGF)作为多尺度分解滤波器,它不仅具有平移不变性与优良的边缘保留特性,且计算效率相对较高,其获取的多尺度子带图像则具有显著的主体特征与丰富的边缘细节。除此外,将MS-RGF与上一节提到的剪切波滤波器相结合,构建滚动引导剪切波变换(Rolling Guidance Shearlet Transform, RGST)[15],它在继承这两种滤波器优点的同时,可实现图像在尺度与方向等两个维度上的最优分解,因此为后续的融合处理奠定了基础。
图像在经过多尺度变换后,通常会对分解后的近似层子带分量图像采用加权平均[16]的融合规则。而对于红外与可见光图像融合,由于两者的光谱特性差异较大,该融合规则均会使融合图像的对比度降低,并且引入一定的伪影噪声。为此本文提出一种“视觉显著性加权”的融合方法,它利用显著特征图作为加权系数,自适应地分配融合权重值。最终在消除两种源图像之间光谱差异性的同时,提高了融合图像的主体观感,有效地避免图像亮度和对比度下降[17]。
“绝对值最大规则[18]”是一种常用的细节层分量融合处理方法,但是很容易引入原始图像的噪声信息。细节层分量主要表征了图像的边缘梯度信息,为此本文提出一种基于“梯度奇异值最大”的融合规则,它通过比较各高频分量的梯度奇异值来输出最终的细节层融合系数,使融合图像更符合人眼的视觉感知习惯。
2 滚动引导剪切波变换
2.1 多尺度滚动引导滤波器
滚动引导滤波器(RGF)作为一种全新的边缘保留滤波器,它可以有效地平滑小结构并恢复边缘,以保留图像最佳主体信息[19-20],表达式如下所示:
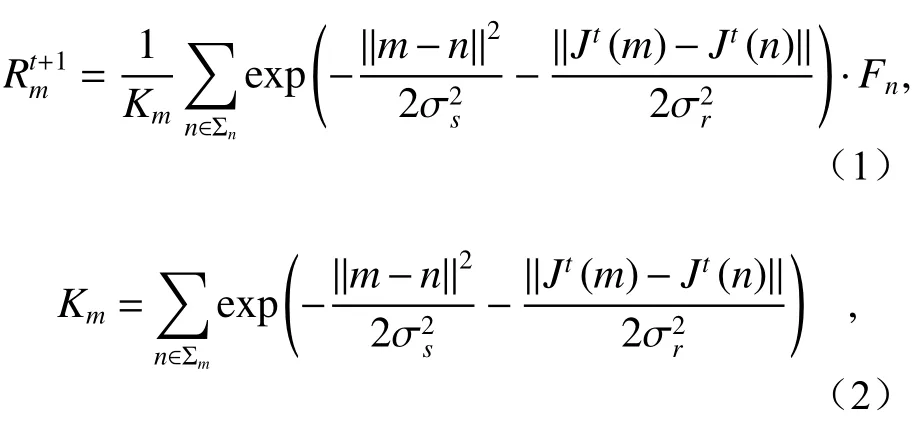
其中输入图像为F,输出图像为Rt,t为迭代次数,σr和σs分别为灰度域和空间域的空间标准差,m与n是图像中的索引坐标,Km为归一化因子,是m的相邻像素的集合。RGF 存在特殊的迭代机制,可将RGF 的滤波过程总结为如下表达式:
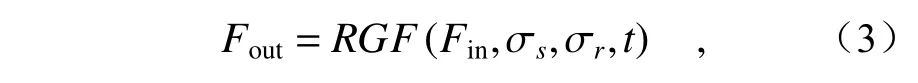
其中Fin与Fout分别表示输入与输出图像,RGF(·)表示RGF 滤波函数。通过改变参数σr和σs,以实现不同尺度层次的图像边缘滤波。
由于RGF 具有灵敏的尺度感知特性与快速的计算速度,将RGF 构建为全新的多尺度滚动引导滤波器(Multi-scale Rolling Guidance Filter, MSRGF),从而有效定位图像的空间多尺度特征,实现图像更为精细的多尺度分解,本文将其定义如下:
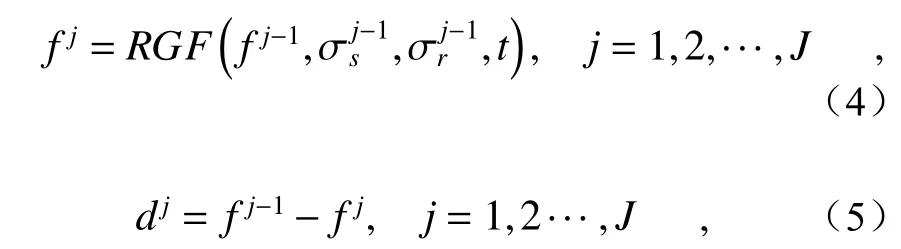
其中fj为第j级滤波后的图像,即近似图像;dj为第j级的细节图像;初始图像为f0,即输入的源图像f;RGF(·) 表示为上一节提到的RGF 滤波函数。一幅图像f经过J层的MS-RGF 分解后可获取一个近似层分量图像与J个细节图像,并且通过简单的线性叠加可获取重构图像f′:
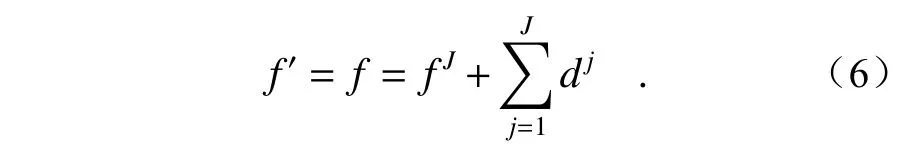
通过式(4)~式(6)可以清晰发现,全新的多尺度滚动引导滤波器在图像分解与重构时不存在上采样与下采样操作,因此可保证该分解框架具有平移不变性。
MS-RGF 的分解效果主要受RGF 滤波函数内部的σs、σr、t等3 个参数影响。对于参数t,它负责控制滤波器内部的迭代次数。如果在图像收敛后继续增大t值,RGF 的迭代次数会随之增加,但输出结果并不能产生较大改变,这显然会影响计算效率,综合考虑,本文选取t=3。除此外,参数σs和σr均为表征RGF 滤波性能的权重指标,两个值的选取往往决定了图像最终的滤波效果。针对参数σs,它主要用于滤波的尺度参数,本文对其设置如下:
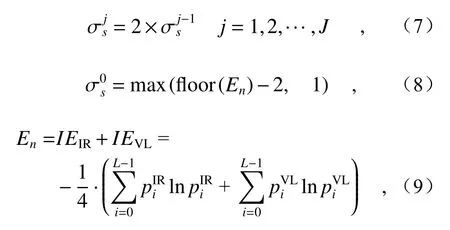
其中L代表图像的总灰度级数,而pi是灰度值为i的像素点在所有像素点中出现的概率,IEIR与IEVL分别代表红外图像与可见光图像的信息熵[21],En代表本文设定的图像联合加权信息熵之和,floor (·)代表向下取整的函数。是最初始的滤波权重,为了能让不同尺度的高频分量包含不同粗细的纹理信息,还需令σs在每一次新的迭代中都逐渐加倍,此时图像的纹理平滑会随之增多,差值计算后的细节纹理也会发生由细到粗的变化。
除此以外,参数σr用于滤波的边缘恢复与保留,其表达式如下:
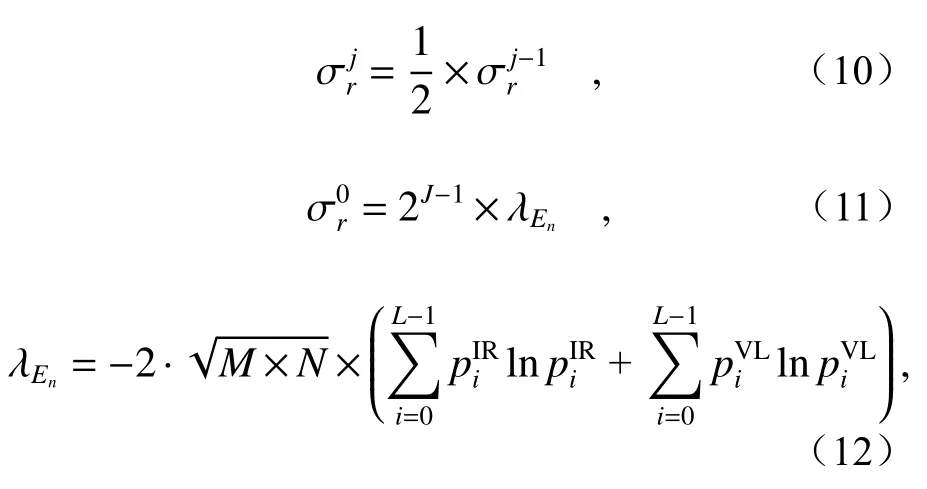
其中L、pi与上述定义相同,M与N为一幅图像的尺寸大小,J为最终的分解尺度, λEn表示本文设定的归一化加权信息熵之和。 σ0r依旧表示最初始的范围权重,它受参数J的影响。为了能在σs逐渐增大的同时,依旧使滤波后的图像保留边缘细节,σr会在每一次新的迭代中都逐渐减半。
图1 详细显示了MS-RGF 的分解子带图。原始图像经过5 次多尺度分解后,获得了最终的1 个近似层子带图像和5 个不同尺度的细节层子带图像。从图1(c)~1(g)中可以清晰发现,随着尺度级别逐渐增加,细节层分量的纹理由细变粗。


图1 基于MS-RGF 分解后的多尺度图像Fig. 1 Multi-scale images decomposed based on MS-RGF
2.2 多方向剪切波滤波器
剪切波具有优良的局部化特性、抛物线尺度化特性、高度方向敏感特性、空间域局部化特性、最佳稀疏特性,它能对图像的边缘曲线进行更为贴近的拟合[22-23]。因此,在其基础上,对MSRGF 分解后的多尺度细节层分量进行多方向剪切波变换,从而有效地提取包含其在内的多方向边缘信息,具体流程如下:
(1)采用Meyer 小波函数w(x) 生成Meyer 窗口函数M(σ),其中两种函数的定义如下:
Meyer 小波函数:
其中对于参数σ,结合局部化窗口的尺寸L×L,将其设置为如下离散形式:
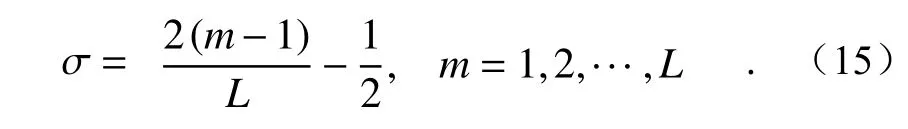
本文设定L=8,此时通过式(13)~式(15),可得到全新的Meyer 小波窗口函数。
(2)利用L=8 的局部化窗口生成伪极化坐标网络,此时网络中每条边的采样点为L+1,即9 个,这里在图2 给出了伪极化坐标网络的示意图。
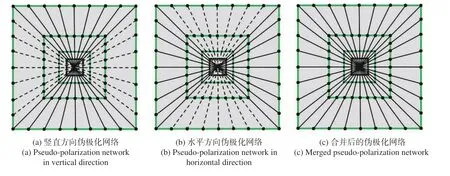
图2 L=8 的伪极化坐标网络Fig. 2 Pseudo-polar coordinate network with L= 8
(3)将步骤(1)获取的Meyer 小波窗口函数放入到步骤(2)中的伪极化坐标网格进行离散重采样,然后把获取的结果再转换到笛卡尔坐标系中,最终生成频域支撑的自适应多方向剪切波滤波器。
(4)对Meyer 小波窗口函数进行平移操作,随后重复步骤(3)的过程。当获取所有方向的自适应剪切波滤波器后,停止之前的操作,最终得到频域支撑的自适应多方向剪切滤波器组ωl,k(x,y),其中l为方向分解尺度,k为分解后的方向数,k=[-2l,···,2l-1],如图3 所示。
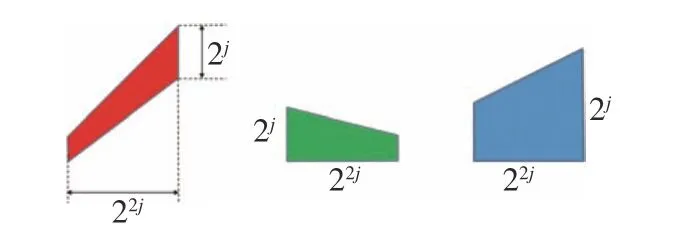
图3 剪切波在频域的滤波器组Fig. 3 The filter bank of shearlet in frequency domain
(5)对频域支撑的滤波器组ωl,k(x,y)进行傅立叶变换,获取时域支撑的自适应多方向剪切波滤波器组Wl,k(x,y)。利用该时域支撑的滤波器组与尺度为j的细节层分量图像dj(x,y) 进行卷积操作,得到最终的多方向细节子带图像(x,y),表达式如下:
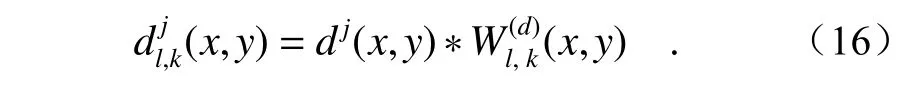
这里将图1 中的第3 级高频分量图像进行多方向剪切波变换以作示例,从而获取其不同方向细节的子带图像,如图4 所示。本文设定其方向分解尺度为l=3,因此会得到8 个方向的细节子带。通过全新构造的剪切滤波器,图像的细节层分量又分为包含不同方向的信息,这样就会在后续的融合图像中得到更为精细的边缘纹理信息。
2.3 滚动引导剪切波变换
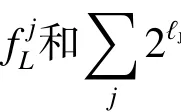
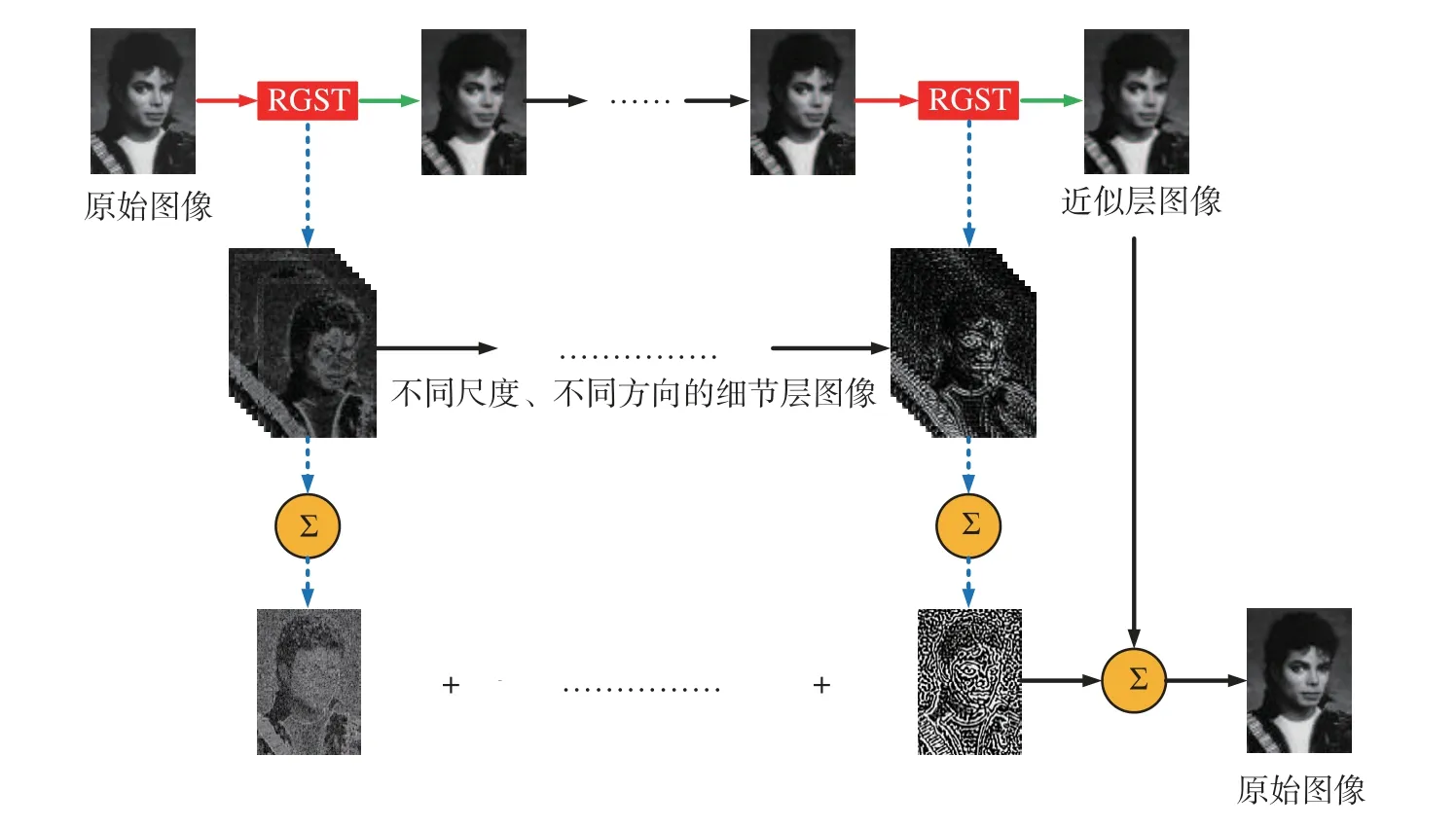
图5 RGST 的分解与重构示意图Fig. 5 Schematic diagram of decomposition and reconstruction of RGST
RGST 的构造借鉴了非下采样剪切波变换(NSST)的思想,相比于NSST,RGST 具有如下优势:
(1)RGST 内部采用了MS-RGF 作为多尺度分解滤波器,它能根据图像的边缘尺度信息进行相应的分解,并且其内部参数也是基于图像特征值而设定的,因此具有很强的自适应性。
(2)RGST 在分解与重构的过程中不存在上采样与下采样操作,并且也不需要满足任何约束关系,只是通过简单的线性差值与叠加计算即可,因此具有平移不变性,计算效率较高。
3 基于视觉显著性加权和梯度奇异值最大的图像融合规则
“图像融合规则”是融合算法的核心,其选取的正确与否则决定了融合图像最终的视觉效果。为此,本文算法首先采用全新的RGST 作为多尺度与多方向分解工具,分别获得可见光与红外图像的近似层分量系数和多方向细节层系数。由于两种图像分量存在本质不同,在融合过程中需要采用相应的融合规则对它们分别进行处理。其中针对近似层分量,提出一种全新的“视觉显著性加权”指导其融合,而“梯度奇异值最大”则作为细节层分量的融合规则,算法示意图如图6 所示。
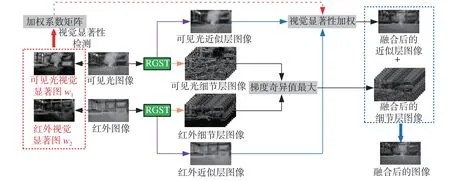
图6 本文融合算法示意图Fig. 6 Schematic diagram of the fusion algorithm in this paper
3.1 近似层图像的融合规则
图像的近似层分量代表了图像的主要能量特征,因此近似层分量的融合规则决定了融合图像的主体视觉效果。人眼在观察一幅图像时,有些区域会引起人眼极大地关注,有些区域则会被忽略。而图像中的目标、高亮区域通常为人眼视觉敏感的显著性区域,以人类视觉机制为基础,构建图像显著性模型[24],将人眼对图像各区域感兴趣的程度使用灰度信息进行量化,即可获得图像的显著图。利用显著图作为加权系数矩阵来指导近似层图像的融合处理,能够有效指导图像内的光谱信息加权融合,在有效地避免图像的亮度和对比度下降的同时,提高了融合图像的主体观感。本文利用改进的FT 算法[25]来获取源图像的视觉显著图,表达式如下:
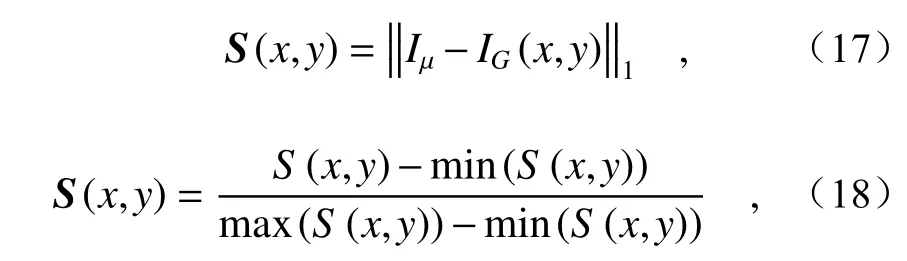
其中||·||1代表向量的ℓ1-范数算符,Iμ为图像中所有像素点的灰度值平均值,而IG(x,y) 为像素点(x,y)经过高斯滤波后的灰度值,其中高斯滤波器的尺寸为3×3,标准差参数σ为π/2.75。对获取的显著性图进行下列操作,可以得到近似层图像的加权系数矩阵[25]:
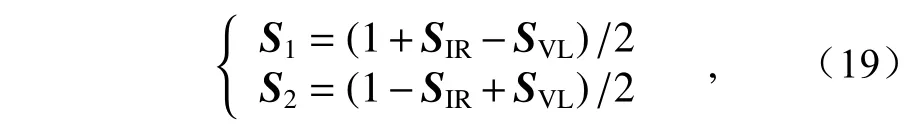
其中SIR与SVL分别代表红外与可见光图像的视觉显著图,S1与S2分别代表红外与可见光图像的权重系数矩阵,只有当两幅源图像的对比度明显不同,一幅接近0,另一幅接近1 时,其权重矩阵才接近于“最大选择法”。但是在大多数情况下,加权法比较适用于对权重矩阵的构造,因此近似层的最终融合规则为:
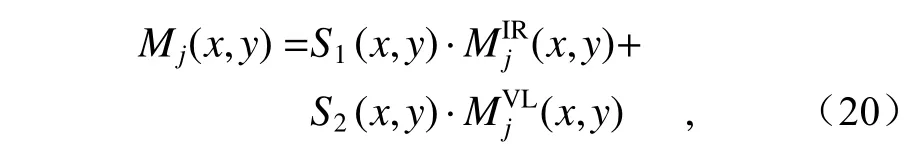
其中M j(x,y)为近似层分量融合后的系数,(x,y)与(x,y)分别为可见光与红外图像近似层分解系数,j是分解层数。
3.2 细节层图像的融合规则
图像的多方向细节层分量反映了图像边缘特征和纹理细节,其融合规则决定了最终的细节层次。红外图像与可见光图像的特征差异较大,红外图像中目标信息表现为高亮度和高强度,“系数绝对值取大”规则容易融入过多的红外信息,从而丢失可见光图像中的细节信息,同时容易误将噪声作为显著特征融入到图像中,因此,本文通过计算细节层分量的“梯度奇异值(Gradient Singular Value,GSV)来指导细节层融合系数的输出,如下所示:
(一)方向梯度和算子(the Sum of Directional Gradient,SDG)[26]一定程度上可以反映图像的边缘细节变化,是反映图像清晰度的关键指标之一,其表达式如下:
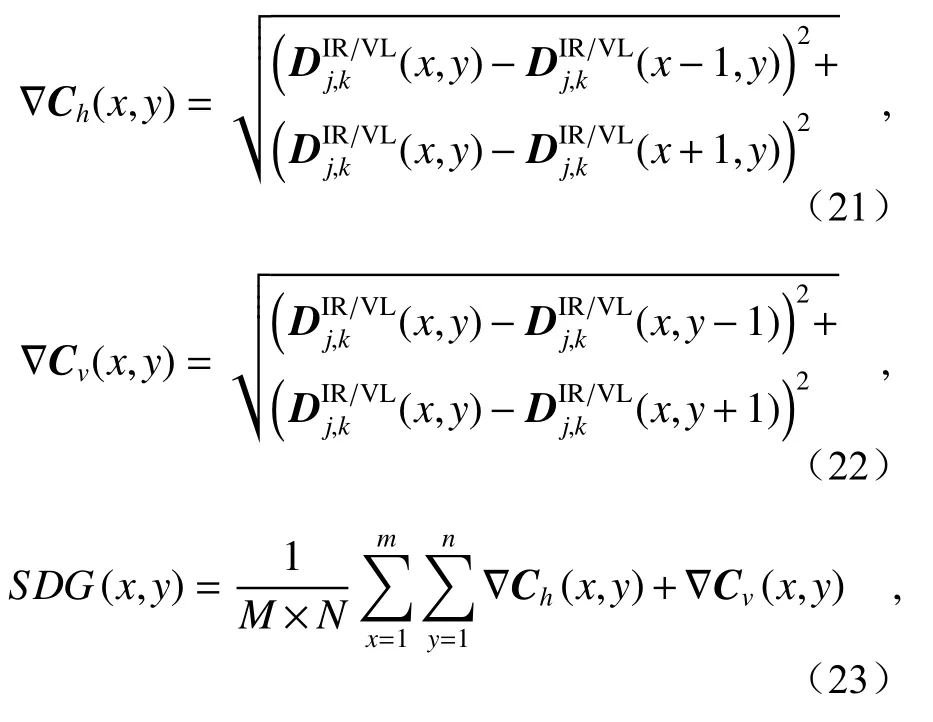
(二)图像的奇异值包含了图像的结构信息,集中了图像的能量特性,能够反映图像的区域特征[27]。受此启发,本文对“方向梯度和算子”进行矩阵奇异值分解,获取梯度奇异值算子,来表征细节层图像的边缘能量特征变化:
(1)对SDG(x,y)进行滑动窗口平移分块,每块矩阵的大小为3×3,中心点为(x,y)。然后对每一子块矩阵进行奇异值分解,其表达式如下:
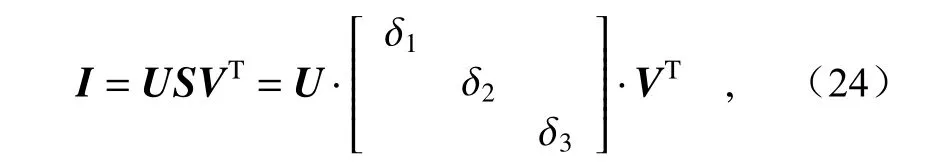
其中I代表分块后的矩阵,δi代表分块矩阵奇异值。
(2)利用其局部区域梯度奇异值构造GSV 算子,其中梯度奇异值越大,局部区域的边缘特征越显著,表达式如下:
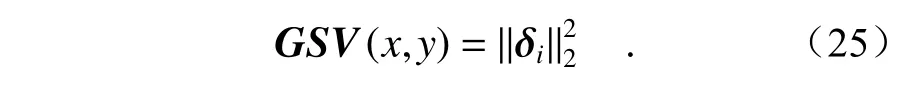
(3)通过“梯度奇异值最大”原则,来确定融合图像细节层系数的输出,能够降低不相干的红外信息与噪声的影响,融入更多的可见光图像细节信息,使图像更适合视觉观察:

其中Dj,k(x,y)为融合后的细节层融合系数。
4 实验结果及分析
为了验证本文算法的有效性,采用CVT[28]、NSCT[29]、ADF[30]、WLS[31]、MSVD[32]、TSF[33]等5 种不同的多尺度分解方法作为对比。为了测试算法的广泛性,选取了5 种不同环境的红外与可见光图像,如图7 所示。其中各组红外与可见光图像已严格配准,而且可以进行下载[34]。

图7 融合实验采用的红外与可见光图像Fig. 7 Infrared and visible light images used in the fusion experiment
对于上述各组对比算法,其多尺度分解工具的实验参数设定如下:
(1)CVT 方法采用“实值曲波基函数”,分解层数为4,分解角度数为16;
(2)NSCT 方法分别采用“vk”和“pyrexc”作为多尺度金字塔滤波器和多方向分解滤波器,分解层数为4,从粗到细的分解方向尺度分别设置为[0, 2, 3, 4]。
(3)ADF 方法利用“各向异性扩散滤波器”获取原始图像的近似层与细节层分量,其内部设置为:t= 10,λ= 0.15,k= 30。
(4)WLS 方法利用“滚动引导滤波器与高斯滤波器相结合的方式” 获取原始图像的近似层与细节层分量,其内部设置为:分解层数为4,σ0s= 2,σr= 0.05。
(5)MSVD 方法采用“2 维矩阵奇异值分解”获得具有不同尺度信息的图像分量系数,其中分解层数为4;
(6)TSF 方法采用“中值滤波器”获取原始图像的近似层与细节层分量,其中分解层数为2,wμ= 30,wg= 3。
对于本文算法,影响其融合效果主要是RGST 工具的分解层数j。为了有效探寻j的最佳取值,本文分别利用第一组与第二组源图像进行融合实验,并依次将j的取值设置为2,3,4,5,6。最终通过计算融合图像的平均梯度(Average Gradient, AVG)[35]与信息熵(Information Entropy,IE)[36]这两个评价参数,从而确定最佳的分解层数,其计算如图8~图9(彩图见期刊电子版)所示。
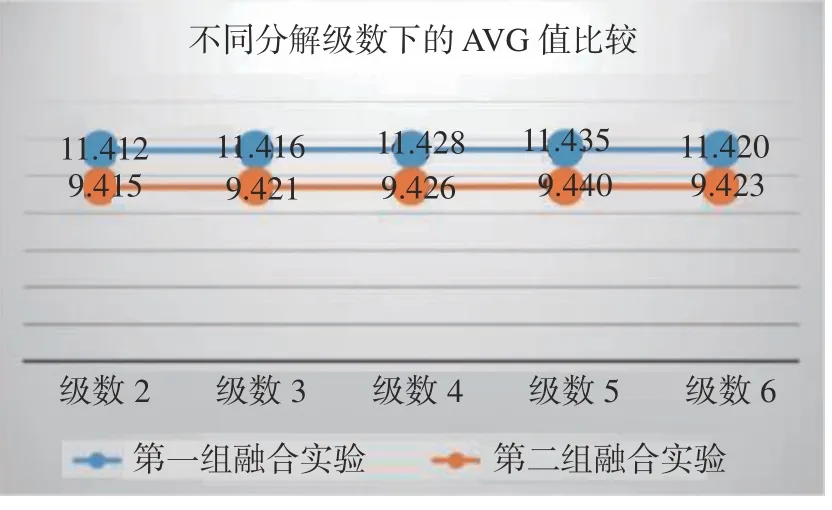
图8 不同分解级数下的AVG 值比较Fig. 8 Comparison of AVG values under different decomposition levels
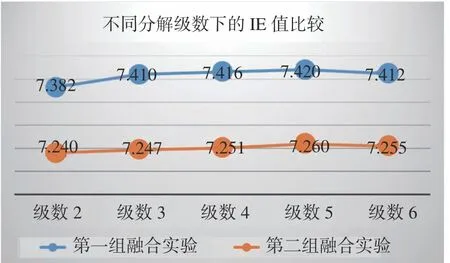
图9 不同分解级数下的IE 值比较Fig. 9 Comparison of IE values under different decomposition levels
通过以上对比可以清晰发现,当j=5 的时候,融合图像的AVG 与IE 值均具有最大值,因此本文RGST 的分解层数j设置为5。对于每个尺度下的剪切波多方向分解向量,为了均衡分解效率与分解效果,设置其为l= [2, 2, 3, 3, 3],剪切波滤波器尺寸向量设置为L= [8, 8, 8, 8, 8]。
4.1 主观视觉评价
图10~图14 分别代表第1 组到第5 组的融合实验,每组图中的(a)~(i) 分别代表红外图像、可见光图像、CVT、NSCT、ADF、WLS、MSVD、TSF 和本文算法的融合图像。在第一组实验中,CVT、ADF、MSVD 等算法的融合图像整体对比度较低,无法清晰分辨出掩体的位置所在。NSCT 的融合图像存在很多伪影噪点,影响视觉观感。WLS 算法的融合图像虽然掩体信息比较突出,但是背景的纹理细节丢失较多。TSF 算法的融合图像与本文方法有着相似的茂密背景信息,但是相比之下,本文方法融合图像的掩体亮度更高,更加清晰,因此相比较之下,本文算法获取的融合视觉性能最强。
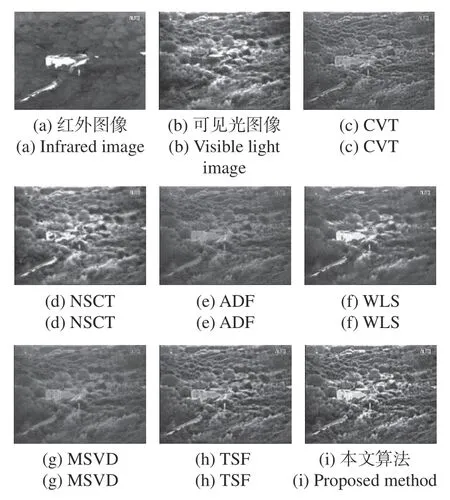
图10 第一组图像融合实验结果Fig. 10 The first group of image fusion experiment

图11 第二组图像融合实验结果Fig. 11 The second group of image fusion experiment

图12 第三组图像融合实验Fig. 12 The third group of image fusion experiment
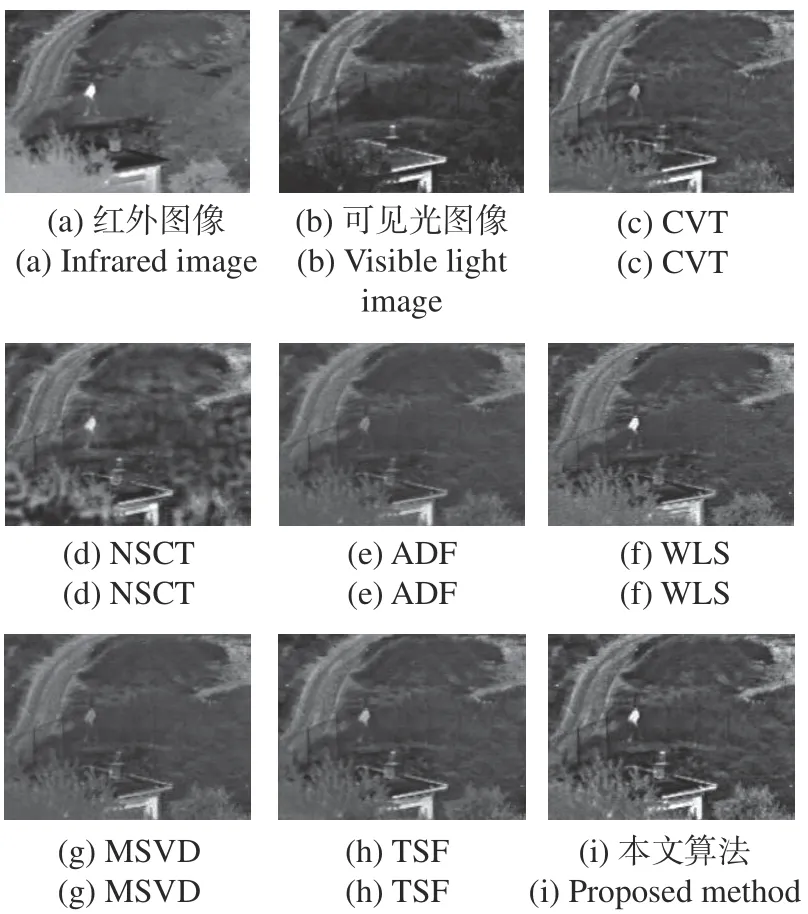
图13 第四组图像融合实验Fig. 13 The fourth group of image fusion experiment

图14 第五组图像融合实验Fig. 14 The fifth group of image fusion experiment
在第2 组实验中,NSCT 融合图像已经无法看清烟雾后的人,WLS 与MSVD 融合算法获取的图像纹理细节丢失较多,其地面的纹理细节已经无法分辨。CVT 与TSF 算法的融合图像在所有对比算法中,融合效果相对较佳,但是和本文算法相比,对比度远不如本文的高,并且细节信息也丢失较多。
在第3 组实验中, CVT、ADF、MSVD、TSF的融合图像仍然存在对比度较低的问题,图像内的人物较暗,NSCT 算法的噪点问题依旧存在,相比于本文算法, WLS 融合图像中汽车的蛇纹涂鸦不清晰,只有本文算法在兼顾两种原始视觉显著性信息的同时,最大程度地还原了原始图像的细节纹理特征。
在第4 组实验中,CVT、ADF、MSVD、TSF等融合算法内的人物亮度都较低,相较原始的红外图像,都存在一定程度的衰减,不利于后续的目标识别处理。NSCT 的人物亮度虽然不低,但是依旧存在的伪影噪声,还是影响了整幅图像的主体观感。WLS 融合图像的树丛没有本文算法的茂密,因此相比之下,本文算法融合图像视觉效果仍然是最佳的。
在第5 组实验中,CVT、ADF、WLS、MSVD、TSF 等算法的融合图像相比于NSCT 和本文算法,其图像对比度都较低,而且图像亮度也不高。而NSCT 算法依旧存在伪影噪点,本文算法的视觉性能是最优的。
综上所述,以上对比算法都能较好地处理融合问题,并且都取得了一定的学术造诣。但是相比之下,本文算法的融合视觉效果更加符合人眼观感。在近似层分量采取的“视觉显著性加权”能最大程度地综合两类源图像的显著性信息;同时“梯度奇异值最大”可以较为全面地将源图像内部的梯度特征添加到融合图像中。因此, 最终的融合图像亮度适中,并且具有较为精细的纹理细节信息、其图像亮度适中、对比度较高、主观观感最佳。
4.2 客观参数评价
一般地,图像融合结果的性能可以通过主观和客观的方式进行评价。在大多数情况下,融合结果之间的差异不大,就难以用主观方式正确地评价融合结果。因此,在客观质量评价的基础上对融合效果进行评价也是非常必要的,本文选取了6 个客观质量指标作为评判标准:(1) 平均梯度(Average Gradient, AVG);(2) 信息熵(Information Entropy, IE);(3) 边缘信息量(Quality of edge, QE)[37];(4) 空间评率(Spatial Frequency, SF)[38];(5) 标准差(Standard Deviation, SD)[39];(6) 差异相关性之和(The Sum of the Correlations of Differences, SCD)[40];(7) 算法运行时间t(单位s)。对于这 7 个指标,除了运行时间,数值越大代表融合算法的性能越好,越大的数值表示融合图像包含的源图像信息越多,但是当图像的局部过曝或者存在噪点时,这些参数也也会虚高,变得不真实,因此客观参数也需要结合主观观感来一起评价。
对于以上指标评价,都是在 PC 主机上采用11th Gen Intel(R) Core(TM) i7-1165G7 2.80 GHz,RAM 16 GB,Windows 10 家庭中文版,MATLAB 2016 的环境下运行的。对于这5 组融合图像,详细的定量评价见表1~表5,其中粗体值表示在上述方法中使用相同索引的最佳结果。
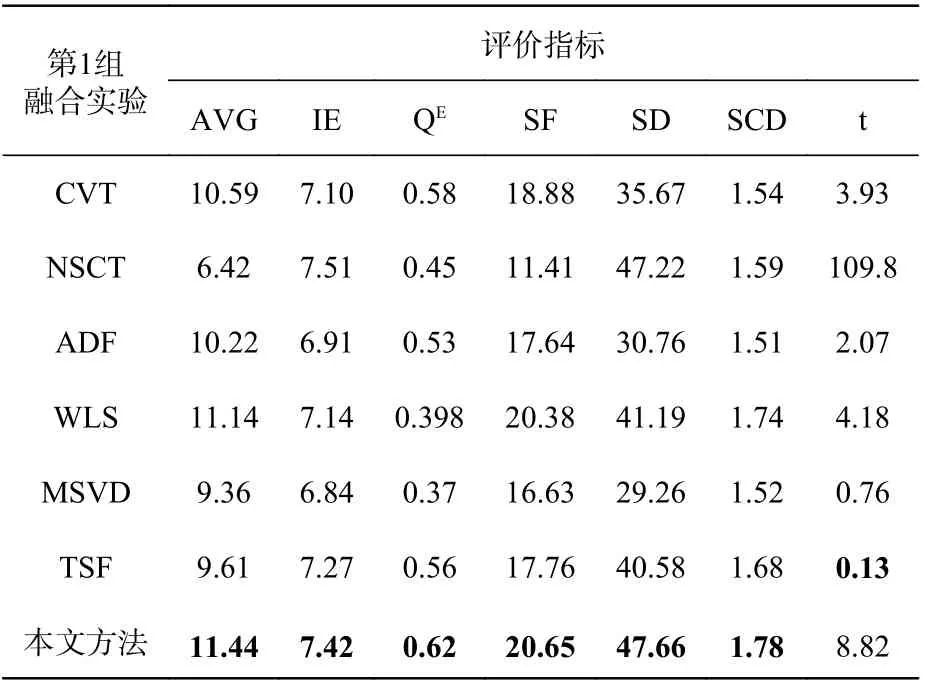
表1 第1 组图像融合实验的客观评价指标Tab.1 Objective evaluation indicators for the first group of image fusion experiments
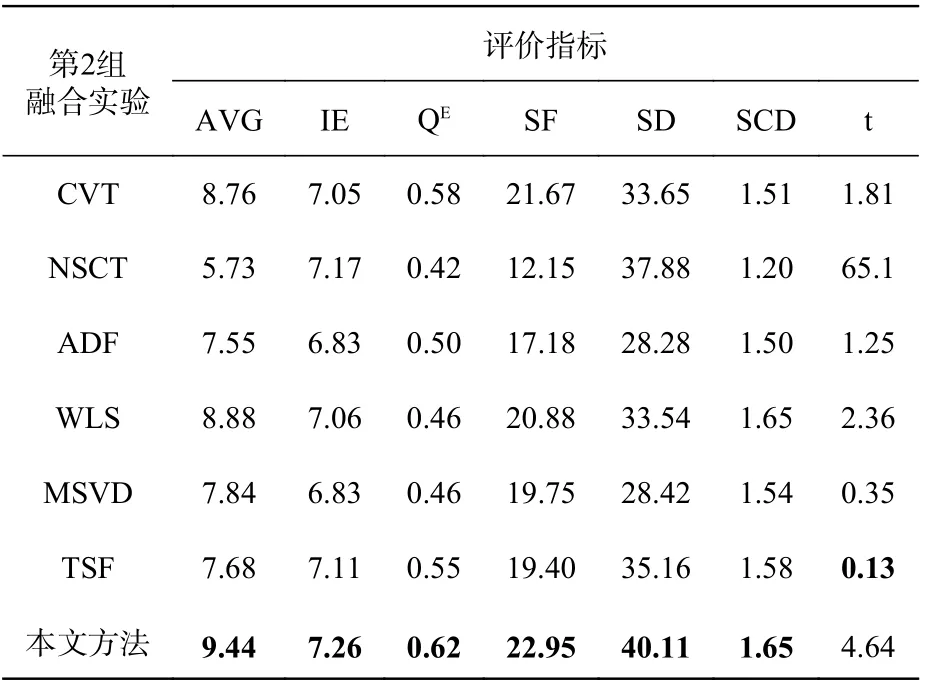
表2 第2 组图像融合实验的客观评价指标Tab.2 Objective evaluation indicators for the second group of image fusion experiments
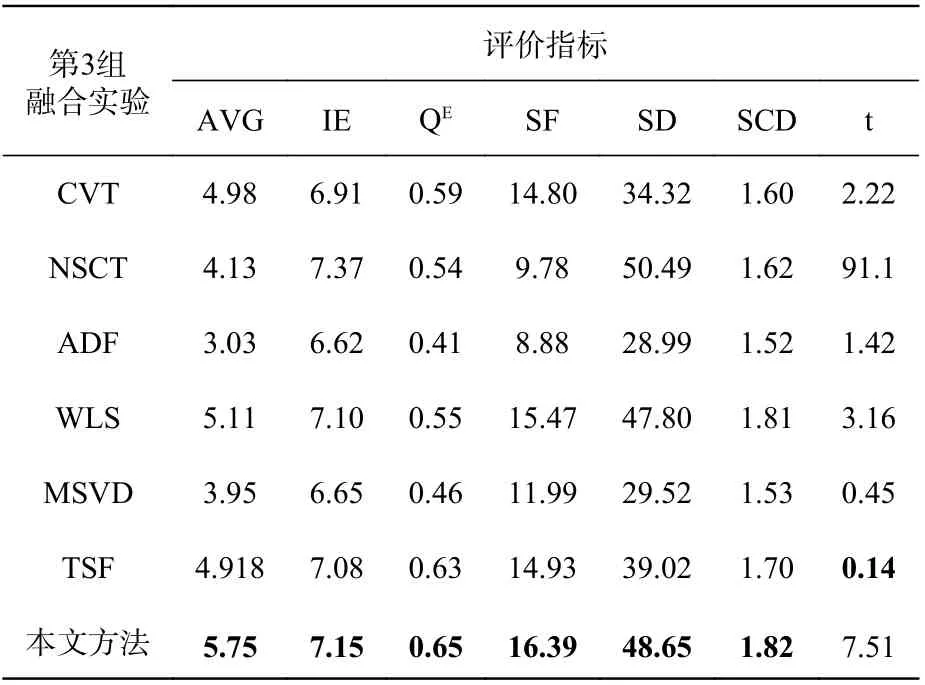
表3 第3 组图像融合实验的客观评价指标Tab.3 Objective evaluation indicators for the third group of image fusion experiments
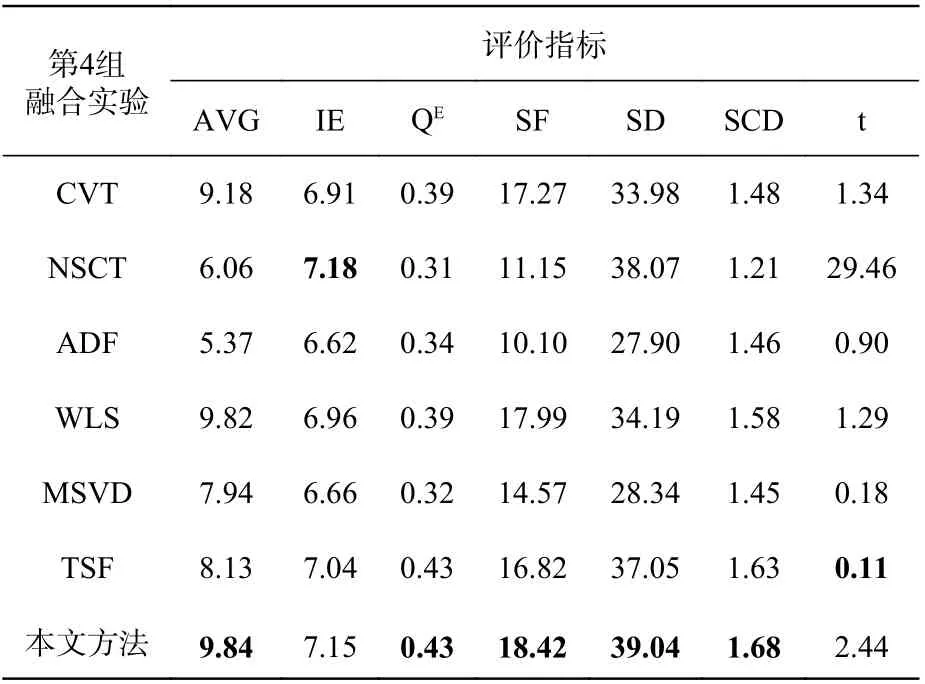
表4 第4 组图像融合实验的客观评价指标Tab.4 Objective evaluation indicators for the fourth group of image fusion experiments
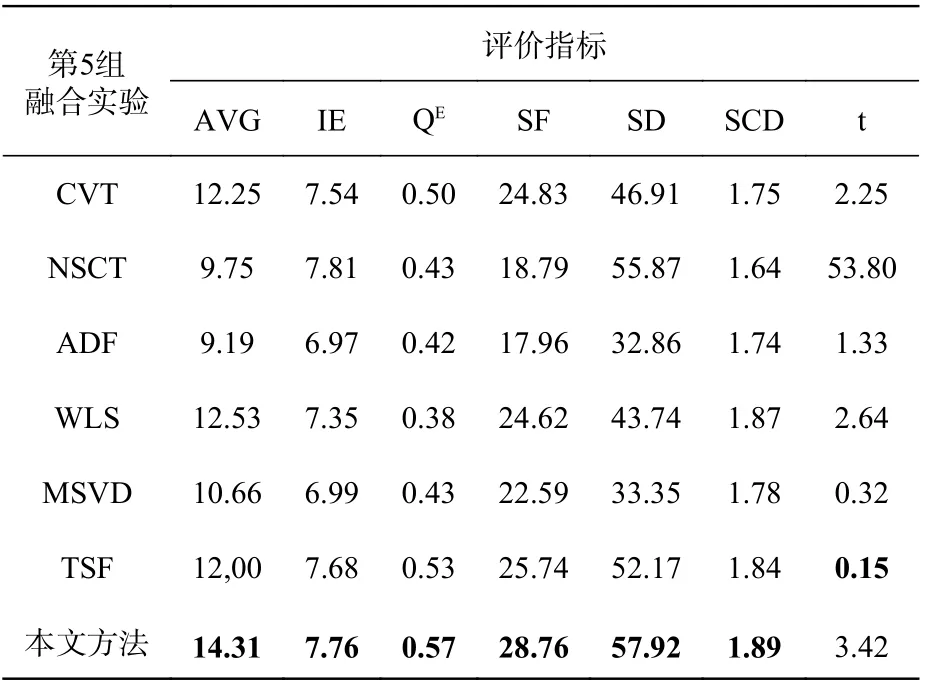
表5 第5 组图像融合实验的客观评价指标Tab.5 Objective evaluation indicators for the fifth group of image fusion experiments
在第1 组、第2 组、第4 组、第5 组实验中,本文方法的各项评价指标均是最优的,这与主观视觉观感是符合的。第3 组实验中,本文算法的IE 值略低于NSCT 算法,但是其它指标仍处于领先。本文还把各算法的运行时间进行了仿真,通过对比来比较算法的时效性。通过实验发现,TSF 算法的时效性是最好的,十分值得肯定。剩下算法的运行时间相差不大,其中本文算法的运行时间排在中间,仅略强于NSCT 方法。由于RGST 同时存在尺度与方向等两个维度的分解变换,同时其内部的参数值也是利用图像的特征值而定义的,因此其整体的运行时间将会有所增加。如果为了追求融合算法的时效性,则可将RGST 内部的参数进行固定的经验值设定,同时减少分解的尺度数和细节方向数,然而这必将会牺牲融合算法优良的视觉性能,因此所提算法的运行时间仍然是可以接受的。
综上所述,所得的客观评价结果与主观视觉效果基本符合。虽然在个别实验中,有些评价值不是最高的,但融合后的图像亮度较高,灰度值过渡自然,拥有较佳的观感。因此在针对红外与可见光融合问题,本文算法似乎更具有一定的针对性,其融合性能略胜一筹。
5 结 论
本文提出一种基于红外与可见光融合的新算法,该算法首先通过滚动引导剪切波变换将源图像进行多尺度、多方向分解。针对近似层分量,采用基于视觉显著性加权的方式进行融合处理;针对细节层分量,采用梯度奇异值最大的规则输出相应的融合系数。为了验证融合性能,采用5 种不同场景进行融合实验。结果表明,该算法一定程度上可以解决红外与可见光图像因光谱差异较大而导致融合图像对比度较低的问题,同时较完整地保留了丰富的纹理信息和细节信息,而且图像过渡自然。该方法在视觉质量和定量评价方面都优于现有的其他融合算法,AVG、IE、QE、SF、SD、SCD 等客观参数指标分别提高16.4%、3.9%、11.8%、17.1%、21.4%、10.1%。

