径节制变位直齿圆柱齿轮的测绘和计算
黄冬英
(江苏省江阴中等专业学校,江苏 江阴,214400)
1 引言
某蝶阀项目要求更换一批齿轮,因蝶阀上的齿轮不是一般的涡轮蜗杆或扇形齿轮,而是由大、中、小三个齿轮啮合传递动力,其中小齿轮是主动轮,小齿轮和中齿轮啮合,中齿轮和大齿轮啮合。为方便描述,小齿轮齿数用Z1表示,中齿轮齿数用Z2表示,大齿轮齿数用Z3表示。拆开齿轮盒后,小齿轮和中齿轮啮合间隙很大,在开关阀的过程中产生了噪音、打齿的现象;并且齿面磨损严重,而大齿轮和中齿轮啮合情况良好,齿廓保持良好。针对该情况,展开数据测量和计算等相关工作。
2 原始数据测量
2.1 齿数
Z1=12,Z2=25,Z3=88,在数齿数时,齿轮齿数少是没什么问题的;不过齿数过多,可以在第一个齿上做好标记,依次往下数,每隔十个齿做一个标记,这种方法可以避免齿数过多而产生混乱,也可以减少检查时间,避免在齿轮计算时把齿数搞错。
2.2 中心矩
小齿轮和中齿轮中心距A实1表示,中齿轮和大齿轮中心距A实2表示。测量时,首先应观察和齿轮相配的轴和轴孔是否有变形、损坏的现象。如果直接拿齿轮测量,由于齿轮轴长短不一,测量时测量点未必能在同一水平面上,再加上齿轮轴与轴孔之间有间隙,受到游标卡尺的作用力,很容易使齿轮位置变动,因此,这样测到的数据未必准确。如果轴孔没有损坏,间接测量孔之间的距离而得到的中心距是比较准确的方法,见图1所示,通过上述测量方法所得到的数据是A实1=48.84,A实2=143.56。
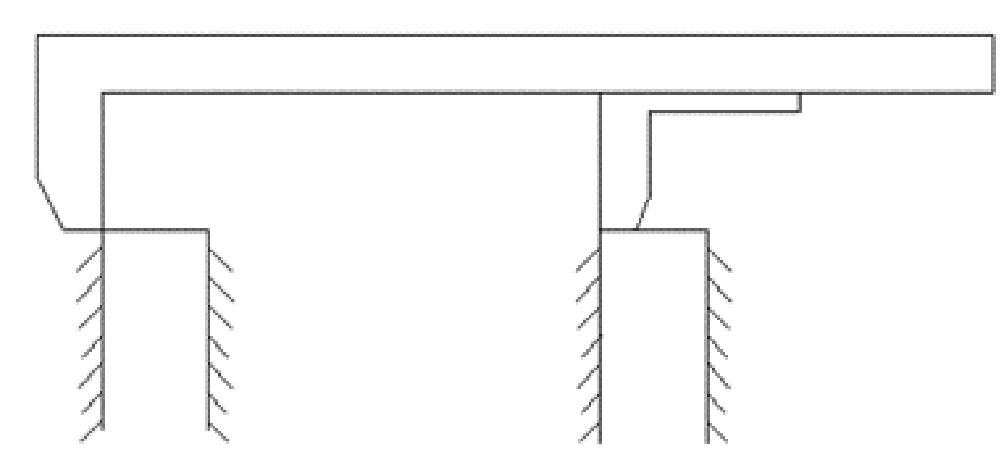
图1 间接测量示意
2.3 齿顶圆
用Da1、Da2、Da3分别表示小、中、大三个齿轮的齿顶圆直径,测量齿顶圆直径时必须注意,只有当齿数是偶数时,才能直接测量;如果齿数是奇数,直接测量的尺寸不是齿顶圆直径,而是一个齿的齿顶到对面的齿槽两齿面与齿顶圆交点的距离(如图2)。显然这个距离比齿顶圆直径小。根据经验,通常将量出的这个距离乘以校正系数K(表1),来求得齿顶圆直径D。
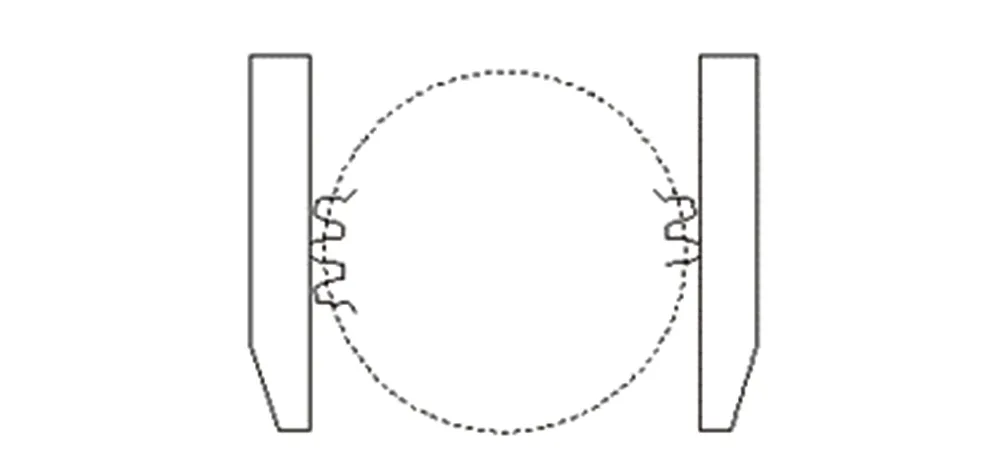
图2 测量齿顶圆
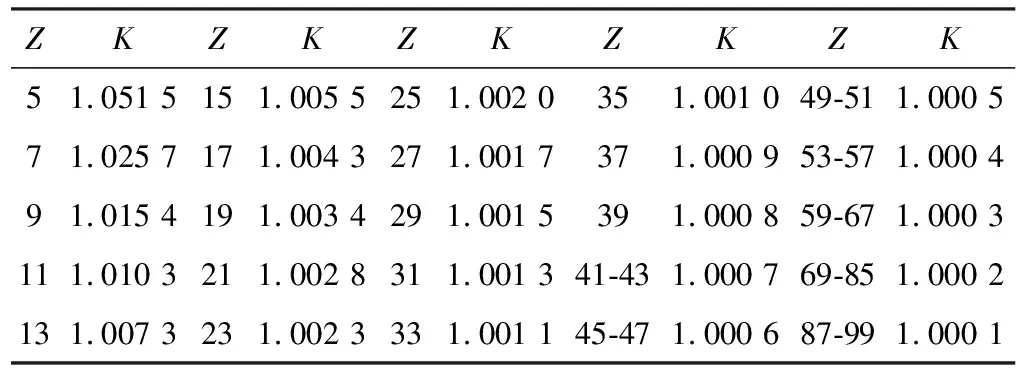
表1 系数表
小齿轮和大齿轮分别为偶数齿,直接测得Da1测=38.24,Da3测=228.48,Da2测=68.4,K=68.53(Z=25,K=1.002 0)根据表1选取[1-2]。
2.4 基节
用t1、t2、t3分别表示小齿轮、中齿轮、大齿轮的基节。这三个啮合的齿轮,如不知道模数、压力角是否为变位齿轮。只能根据齿轮上测量的数据来判定,而为什么要测量基节,因为从渐开线齿轮原理可知道,基节只与模数和压力角有关,而与其他一切参数无关,所以,通过测量基节来推算模数和压力角是非常直观的。
基节的测量可以用基节仪直接测量,基节仪使用不便,使用条件受限。如果齿轮的粗糙度达不到要求,很难准确测量,由于并不配备此设备,所以只能寻找其他方法。
通过渐开线齿廓齿轮原理可知,发生线上的线段的长度等于基圆上被滚过的弧长,(渐开线的形成及其特性在这里不再赘述,可以参照齿轮原理)。基于这个特点,可以通过测量公法线长度来间接求得基节的长度,公法线长度公式为:
LN=(N-1)t+8
(1)
式中,LN—跨N个齿的公法线长度;N—跨齿数;t—基圆长度;S—基圆齿厚。
公法线长度公式的由来,可以参考图3所示。
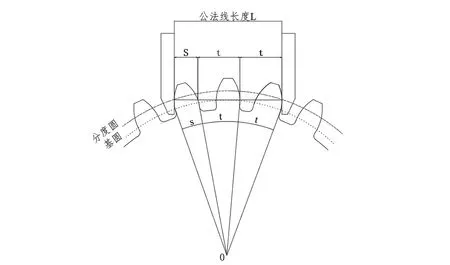
图3 公法线长度
注意:变位齿轮的公法线长度计算公式有别于直齿圆柱齿轮的公法线长度计算公式(图4所示),在这里为更清晰地阐述利用公法线长度差的方法来测量基节,特给出变位齿轮(包括高度变位齿轮和角度变位齿轮)的公法线长度计算公式:
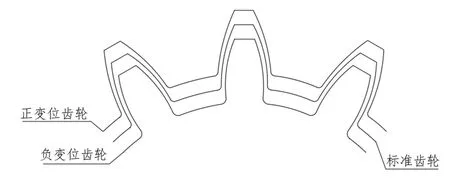
图4 齿轮示意图
L实=LN+2Xmsinα
(2)
式中:L实—变位后的实际公法线长度;LN—未变位的跨N齿的公法线长度;N—跨齿数;X—变位系数(代入公式时,需加正负号);m—模数;α—齿形角(分度圆压力角)。
由图4可明显看出L+>L>L-。由式2可得出:
t=LN-LN-1
(3)
进一步证明了基节与变位系数无关。
当测量跨齿数时会发现这样的现象,如果齿数跨多了,卡尺就会与齿轮牙齿上部分接触;如果跨齿数少了,就会在齿轮根部接触,都不会是准确的测量值。测量时只有把卡尺卡在大约牙齿中部的位置,才能得出准确值。因此,测量时跨齿数的选择尤为重要,公式(4)可供参考。
(4)
式中,α在压力角为未知数,可依次用14.5°、15°、20°、22.5°代入验算。
由上式得出的值不是正整数,可四舍五入来最终确定值。由于基节关乎压力角和模数这两个重要的齿轮数据,虽然测量时难免会有误差,为保证测量值尽量准确,可采用多次测量取平均值的方法。对于小齿轮、中齿轮、大齿轮则分别测量五组数据,(选用20°代入式4)数据如表2~表4所示。
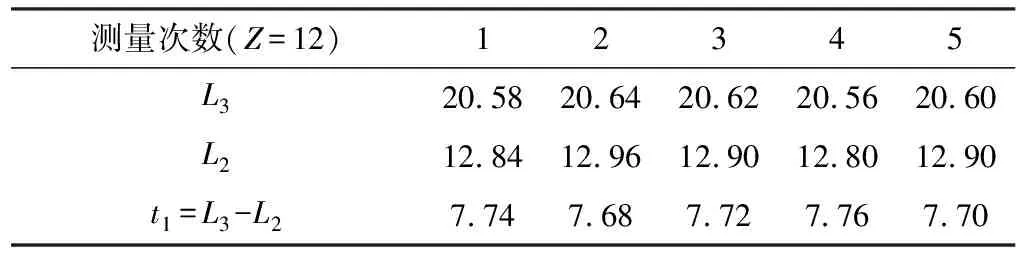
表2 小齿轮数据
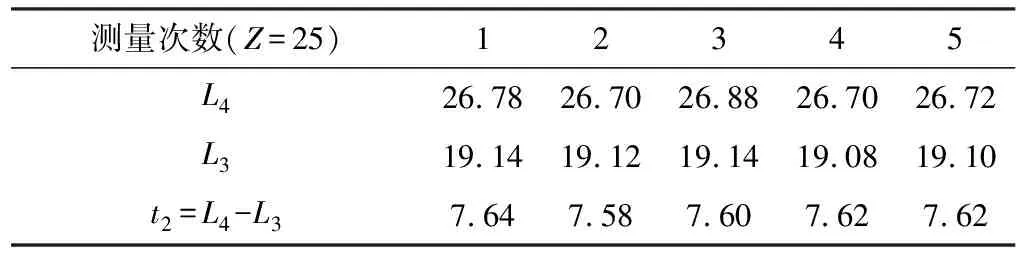
表3 中齿轮数据
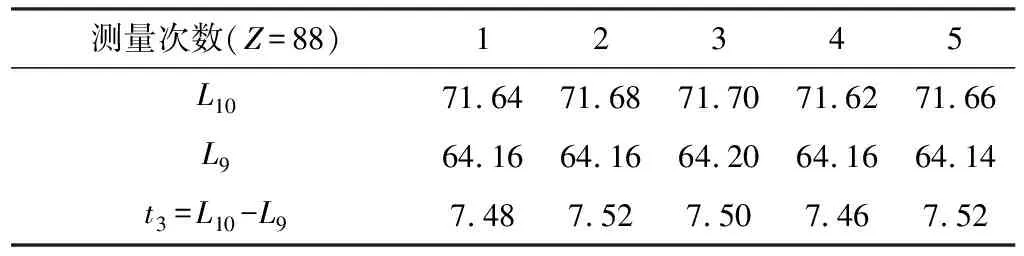
表4 大齿轮数据
整理上述数据可得出t1=7.72,t2=7.612,t3=7.496。对比这三组数据,发现基节依次变小,数据测量是否有误,如果正确,该采用哪组数据,为何会出现这种情况?
先分析数据,第一:为何三组数据的平均值会出现如此大的差距?第二:小齿轮和中间齿轮同样测量跨齿数是3;为何数据会有将近1.5 mm的差别?很明显,一对渐开线齿轮的正确啮合条件是它们的基节必须相等。再观察小齿轮,当测量跨两个齿时,卡尺很接近齿根了,而测量3齿时,接近于齿中部,所以所得的差值必然会大,小齿轮的齿数只有12齿,为保证加工时不发生根切现象(不发生根切现象的最小齿数为17齿),这个齿轮必须采用正变位齿轮,增加它的齿强度。小齿轮端部尖而细,进一步证明了它应该是变位齿轮。同样,中齿轮齿数也因为齿数少,在测量跨齿数3的公法线长度时,卡尺也无法卡在齿中部位,所以所得值会有偏差;第三组数据,齿数足够多,卡尺在测量9齿的公法线长度和10齿的公法线长度都在齿中部位,所以接近准确值,因此采用第三组数据,即t=7.496,基节的计算公式为:
t=πmcosα
(5)
通过查基节函数表(模数、压力角的乘积值表,因为压力角数量有限)可知当m=2.54,α=20°时,t=7.498,与所测得的值相近。模数已经标准化了,一般国际标准化组织,如中国、德国、日本、法国、瑞士等采用模数制,而美国和英国一般采用径节制。
在标准化模数中,没有2.54这个模数,该案例是按照美标的,因此,这个齿轮设定为径节制,暂定m=2.54(P=10),α=20°,通过其他数据来印证假设[3-5]。
2.5 全齿高
三个齿轮的全齿高分别用h1、h2、h3来表示,测量全齿高可以利用游标卡尺的测深度尾针测出。由于尾针的自身厚度,卡尺尺身的宽度不够,测量的数据不够准确,测量出来的值没有价值,只能供参考,h1=4.62,h2=5.60,h3=5.68[4]。
3 数据计算[6-7]
首先用标准直齿轮代入公式计算,既然知道了齿数,暂定了模数,利用这两个数据来确定标准中心距,然后再与实际中心距比较,由标准齿轮中心距公式可知:
已知齿顶圆直径,利用标准齿轮齿顶圆计算公式,齿顶高系数暂定为ha*=1(在德标中有0.8,美标的短齿系列为0.875,多用于汽车离合器中,这些都不太常见,所以暂定为1),由齿顶圆公式可知:
Da1=(Z1+2)mDa1=35.56
Da2=(Z2+2)mDa2=68.58
Da3=(Z3+2)mDa3=228.60
由前期的数据测量就已经可以判断小齿轮为变位齿轮,从得出的数据进一步验证了判断,小齿轮为正变位齿轮;而对于中齿轮和大齿轮为标准直齿圆柱齿轮。(高度变位齿轮的中心距与标准中心距相等,只测出中心距而得出齿轮为标准齿轮的结论是不准确的),由于三个齿轮相互啮合,所以齿形角、模数、齿顶高系数、顶系系数全部相同,通过中齿轮和大齿轮先确定一些参数。
理论全齿高可知:
h=(2ha*+c*)m,得到h=5.715
三个齿轮全齿高的测量值中,大齿轮的数值接近。当齿顶高系数ha*=0.8时,c*=0.1~0.3,代入公式中可得h=4.318~4.826。
如果是美标短齿系列,即ha*=0.875,c*=0.125,代入公式中可得:h=4.762 5。
上述两个计算值说明这套齿轮副的齿顶高系数ha*=1,顶系系数c*=0.25。
对于小齿轮,计算稍微会复杂些。首先,已经确定小齿轮为正变位齿轮,当齿轮齿数小于17齿时,齿轮加工就会产生根切现象(根切现象的产生,可参考齿轮加工),为保证零件结构的紧凑性,设计者往往会尽可能地减少齿数,但如何解决根切问题,齿轮变位往往是很好的选择。
加工齿轮时,为了避免根切,齿数越少,需要刀具做更大的位移,即齿轮的变位系数越大;但避免根切的最小变位系数是多少呢?公式(6)就是最小变位系数公式:
(6)
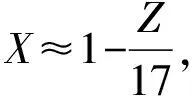
(7)
由于变位齿轮的中心距变化,所以齿面的受力方向与运动方向的夹角就有了变化,即啮合角不再等于分度圆压力角:α啮≠α;啮合角的大小直接影响变位系数,给出啮合角公式:
A实cosα啮=Acosα
(7)
式中,A实—实际中心距,A—标准中心距,α啮—啮合角。
由已算出的数据可知:cosα啮=0.904,α啮=25°17′52″。
已知啮合角,可以求出总的变位系数,给出总变位系数公式(8):
(8)
式中,X—总变位系数,由已知数据可知:X≈0.8。X1—小齿轮变位系数,X2—大齿轮变位系数,Z1—小齿轮齿数,Z2—大齿轮齿数。invα=tanα-α,可以查渐开线函数表。由于上文中,已确定中齿轮为标准齿轮,即X=X1=0.82,X2=0;又已知,变位系数与中心距变动系数和齿高变动系数三者之间的关系为:
X=y+△y
(9)
式中,△y—齿高变动系数(齿顶降低系数),y—中心距变动系数(分离系数),可求得y。
(10)
从而计算得到y=0.728,△y=0.092。
进而可求得齿顶高ha和齿根高hf:
ha=(ha*+X-Δy)m
(11)
hf=(ha*+C-X)m
(12)
经计算可得齿顶高ha和齿根高hf:ha≈4.39,hf≈1.09。
由此可根据以下公式,计算得到h和Da。
h=ha+hf
(13)
Da=d+2ha
(14)
得到,h=5.48,Da=39.26。
公法线长度LN:
LN=L+mXsinα=
mcosα[(N-0.5)π+Zinvα]+2mXsinα
(15)
LN——变位齿轮公法线长度,L——标准齿轮公法线长度,N——跨齿数
在上文中已经测量了小齿轮跨3齿的公法线长度L3,通过所给公式,求得跨3齿的公法线长度L3≈20.60。
4 数据分析
测量的数据中,小齿轮的齿顶圆直径Da实=38.24,而求得的齿顶圆直径Da求=39.26,齿轮在工作时,齿顶圆不会有磨损,为什么会出现将近1 mm的差距呢?首先检查所求的数据,通过查图表,可以简单判断变位系数选择是否正确。从《机械设计手册》查变位系数与总齿数和齿高变位系数之间的关系图表可知,通过图表可以大致判断,当总齿数为37,变位系数为0.82时,齿高变动系数在0.09~0.10之间,通过图表,计算出来的数据是正确的。当齿数较少时,如果变位系数过大,就可能发生齿顶过薄[8]。
齿顶厚公式为:
(16)
(17)
(18)
(19)
式中红,Sa—齿顶厚,αa—齿顶圆压力角,rb—基圆半径,ra—齿顶圆半径,d—分度圆直径。
通过上述可求得:αa=43.15°,求得齿顶厚Sa≈0.438 8。
从图5可发现,小齿轮的后齿顶非常尖,而所求得的齿顶厚也证明了这一点,那么唯一的可能就是:由于齿形过于尖,原设计在机加工阶段,车掉了一部分齿顶圆,如图6所示。
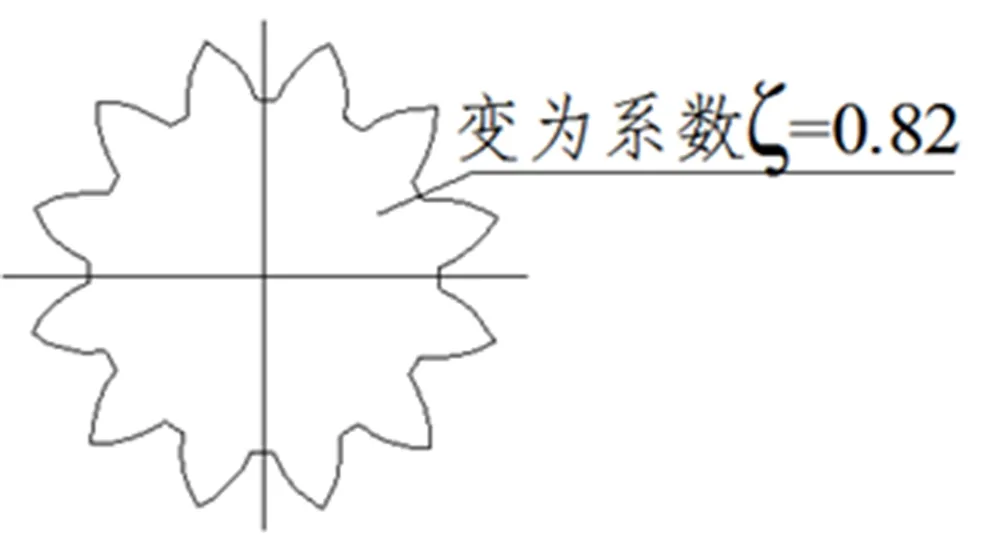
图5 齿顶圆示意

图6 齿顶圆加工示意
接下来再来校核小齿轮的重合度ε:
(20)
由公式16~公式20可求得重合度:ε≈1.26>1.2。

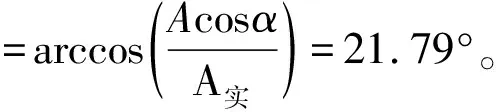
中心距变动系数△y=0.01,分度圆直径d=33.02,齿顶圆直径da=35.476,全齿高h=5.69,公法线长度L3=19.62,跨齿数:N=3(根据变位齿轮跨齿数公式),重合度ε≈0.98<1.2。
增加一个齿后,重合度小于许用重合度,所以,齿数不变。两齿轮的啮合情况如图7所示:
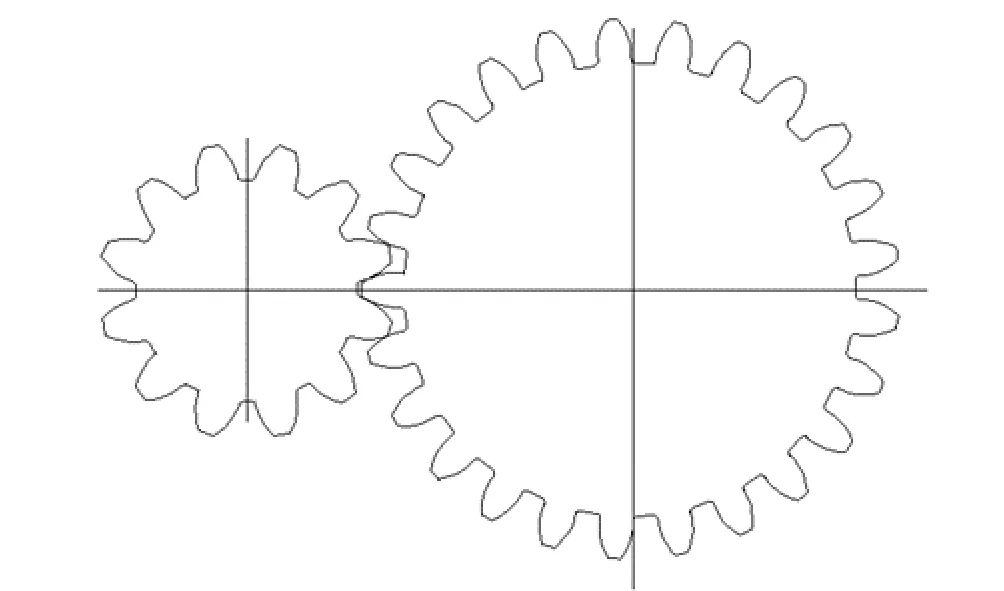
图7 啮合图
5 检验
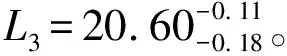
虽然齿轮主要参数有了,但是齿轮的传动精度和公差如何确定?该给出哪些参数呢?根据齿轮的使用要求对齿轮制造精度主要有四个方面的要求:
(a)运动精度
主动轮每转过一定的角度,从动轮应按照传动比准确地转过相应的角度,但是由于齿轮本身的制造误差,不可避免地会出现实际转角与理论转角之间的差异。
(b)工作平稳性
当齿轮在高速运转时,由于齿轮的瞬时传动比变化,就会引起震动和噪声,进而降低齿轮的使用寿命。
(c)接触精度
齿轮在传递扭矩时,一对啮合的齿轮不可能达到全部齿面接触,接触面积越大,受力越大,则接触精度越高。
(d)齿侧间隙
相互啮合的一对牙齿在不接触的一面通常会留有间隙,称之为齿侧间隙,为防止卡齿,并在齿面上形成油膜润滑,两齿之间通常会有间隙,如果间隙过大,齿轮传动噪音就大,降低齿轮使用寿命。所以为了保证有较好的使用性能,对运动精度、工作平稳性、接触精度和齿侧间隙有一定要求。
选择齿轮的精度等级必须要根据齿轮传动用途、工作条件和加工条件三个方面综合考虑选择精度等级。一般来说,由于齿轮传动的具体工作条件不同,对上面所述的精度要求也不一样;一是高速传动齿轮,对工作平稳性的要求是最主要的;二是对低速重载齿轮而言,接触精度是最重要的;三是仪器上读数的齿轮,运动精度是最重要的[8]。
本齿轮使用在蝶阀上,为手动开启,所以转速不高,对平稳性和运动精度要求不高,因此,选择精度等级为:8-9-9-Dc。第一位数“8”代表运动精度等级为8,第二位数字“9”代表工作平稳性等级为9,第三位数字“9”代表表示接触精度等级为9,最后一位字母“Dc”表示齿侧间隙为标准保证侧隙。
齿轮的精度等级选定后,加工时应该选定以下尺寸公差才能确保齿轮达到精度要求:
5.1 运动精度检验项目
5.1.1 齿圈径向跳动公差Fr
从齿轮的牙齿或齿间的固定弦至回转轴心的距离的最大允许变动量。
5.1.2 公法线长度变动公差Fw
在同一齿轮上,相同跨齿数,公法线的最大长度和最小长度的差值。
5.2 工作平稳性检验项目
5.2.1 齿形公差ff
在牙齿工作部分内,容纳实际齿形的两理论齿形间的最大允许的法向距离;在垂直于齿轮回转中心线的剖面内相对于轴心线来测定。
5.2.2 齿距离、偏差fpt
齿轮上相邻两个同名齿侧的两条互相平行的切线间的实际距离与公称基节的最大允差和最小允差。
5.3 接触精度检验项目——齿向公差fβ
在通过齿高中部的圆柱上,在齿全长内实际齿向对理论齿向的最大允许误差。如何同时检验齿圈径向跳动公差和公法线长度变动公差才能确保运动精度?
滚齿的加工是靠分齿运动,即滚刀与齿坯之间按一定速度比均匀旋转运动来保证分齿均匀的要求,因此机床工作台回转不均匀是造成滚齿后齿轮牙齿分布不均匀的重要因素。在测量公法线长度时,就会出现最大值和最小值,而控制这个差值,就可保证运动精度。但是,控制公法线长度的差值,只能保证牙齿相对于工作台回转中心的运动精度,可是齿轮是要使用在零件上的,所以齿轮在使用时,必须使牙齿相对于与其相配合的轴或轴孔的回转中心是均匀的。因此控制齿圈的几何中心与内孔中心的偏心量,通过测量齿圈径向跳动来反映这个偏心量。公法线长度变动和齿圈径向跳动分别反映了滚齿时两种不同性质的误差:即工作台回转误差和齿坯安装误差,只有同时限制了公法线长度变动和齿圈径向跳动才能保证齿轮的运动精度。
如何同时检验齿形公差和齿距偏差才能确保工作台的平稳性呢?齿轮的齿形面不可能与理论的渐开线完全吻合,必须限制齿形面的误差来保证牙齿从开始啮合到脱开的过程中速度比的变化;另外,如果保证了齿形面与渐开线吻合,可又不控制相邻两齿之间的距离(即齿距),无法保证传动时,一对牙齿过渡到另一对牙齿啮合过程中速比的变化而引起冲击和噪音。因此,齿距的偏差也是影响齿轮工作平稳性的主要因素。
如何检验齿向误差才能保证接触精度?在齿面上沿齿宽和齿高两个方向的接触面积百分比来反映齿轮接触精度,齿向误差是直接影响着齿宽方向的接触面积百分比,由于影响齿高方向接触好坏的因素是齿形公差和齿距偏差。这两个项目已经在工作平稳性上规定了,没必要再次规定限制,所以只限制齿向误差即可。但是,如果单独分析提高齿轮接触精度时,就不能只考虑齿向误差,也要考虑齿高方面的影响因素[9-10]。
6 结束语
通过以上阐述,了解了各项精度要求,可通过查表来确定各等级下的公差是多少。通过选取整理,各项数值分别为:Fr=0.05,Fw=0.03,ff=0.03,fpt=±0.05,fβ=0.03。由于此齿轮转速不高,载荷不大,所以就用加工齿轮最常用的材料45钢,调质处理,表面硬度为HB=220~250。

