基于SSA-ELM的动力电池健康状况预测研究

王亦乐 黄宏成 杨健 徐世琦 尹明轩

(1上海交通大学，上海 200240;2上汽大众汽车有限公司，上海 201805)

0 引言

近年来，为了应对能源与环境危机的双重威胁，用更加清洁的电动汽车取代传统燃油车成为一种潮流。而动力电池作为电动汽车的核心模块之一，也随之迅速发展。然而，在电池产量和性能不断提升的同时，电池的安全性却时常引发人们的担忧。随着电池使用时间的增长，电池内部的活性物质会不断损耗造成电池性能的退化，这不仅会导致电池储存和输出能量的效率降低，更会导致因电池内部短路引发自燃甚至爆炸等严重事故的风险提升。因此电池健康状况(state of health，SOH)和剩余使用寿命(Remaining Useful Life，RUL)预测是确保电池使用安全重要手段之一。SOH一般定义为在某一条件下电池可放出容量与新电池额定容量之比，而RUL则定义为电池SOH从当前状态下降至某一阈值(一般为80%)所需的时间。

研究者们已经提出了众多的SOH预测方法，根据原理可主要分为3类：基于模型的方法、数据驱动的方法和混合方法[1]。由于基于模型的方法往往存在描述不准确和泛用性较差等问题，近年来数据驱动方法和混合方法成为研究热点。徐佳宁等利用改良蚁狮优化的支持向量回归进行预测，改良蚁狮优化提升了惩罚因子和核参数的搜索效率和收敛精度[2]。赵沁峰等利用遗传算法优化的极限学习机进行预测，通过遗传算法优化网络隐含层参数避免了随机赋值导致的结果波动问题[3]。王义等通过BiLSTM模型对数据进行双向分析，在传统LSTM的基础上进一步提升了预测精度和稳定性[4]。Zheng等通过RVM生成未来观测数据，解决了经验模型中更新参数所使用的滤波方法只能提供短期估计的问题，提升了衰退后期的预测精度[5]。赵沁峰等则利用经验模态分解将衰退过程分解为波动分量和趋势分量，并利用不同的数据驱动方法进行分析(Arima&GRNN)，取得相比单一模型预测更高的精度[6]。

但是，目前提出的这些预测方法一般都以可控条件下的充放电实验数据作为支撑。而实际运行中的车辆电池数据变化情况更加复杂，且受到噪声干扰更大，使用这些方法难以取得理想的效果。因此，本文提出了一种基于麻雀搜索算法优化的极限学习机的两步式电池SOH预测算法，用于实车电池数据的分析和预测。

1 SSA-ELM模型搭建

1.1 ELM基本原理

极限学习机(Extreme Learning Machine，ELM)是一种在BP神经网络的基础上改良的新型单隐藏层的前馈神经网络[7]，其网络结构如图1所示。该算法相比传统神经网络，特点在于隐藏层的权值和偏置是在模型的初始化阶段随机赋予或人为给定的，在训练过程中不进行更新。训练过程实际仅求取输出层权值，仅仅通过矩阵的求逆计算就能够获取其唯一最优解。因此该方法具有学习速率和泛化能力方面的优势，并且支持在线学习和动态更新。

图1 极限学习机结构

ELM的数学描述如下：对于一个给定的L维输入向量x，令预期输出为M维的输出向量y，通过一个隐藏层结点数为z的网络进行计算的公式为：

(1)

式中：wi为L维的隐藏层权重向量；bi为隐藏层的偏置；βi为M维的输出层权重向量；g(*)为激活函数。

利用矩阵形式对式(1)进行简化得：

Hβ=T

(2)

式中：H为K×z维的隐含层输出矩阵；β为z×M维的输出层权值向量；

(3)

因此，该网络训练目标是使式(2)中的误差函数最小：

min‖Hβ-T‖

(4)

该问题被证明具有唯一最优解：

β=H+T

(5)

式中H+为H的Moore-Penrose广义逆矩阵。

1.2 SSA参数优化

由于ELM的隐含层权值是随机赋予的，导致其预测结果存在较大的波动性，对预测精度与可靠性造成了影响。因此采用麻雀搜索算法(Sparrow Search Algorithm，SSA)对这些参数进行优化[8]。

首先建立包含n个麻雀的种群：

(6)

式中：矩阵的每一行代表一只麻雀，即一组候选网络参数；d为待优化的参数维度，即网络中隐含层权重与偏置数量之和。

接着计算每只麻雀的适应度f，并根据适应度对种群排序。

初中生需要解决的动点问题不仅是初中数学中某一章节的内容，也是初中学习期间所有数学知识的集成与结合，并在考试中占有较大的分数比重。也正是在其综合特性影响下致使学生在解答“动点问题”期间经常感到无从下手，在实际教学期间也缺少针对性教学方法与模式的教学内容。所以，在对“动点问题”教学期间，应对学生解答问题时具有的难点与其形成原因进行深入分析，结合学习需求制定完善的教学方法。在提高数学教师教学效率的同时，也可促进学生成绩的提高，在一定程度上对提高学生问题解决与分析能力也有着极为重要的作用。

之后，适应度最高的一部分个体将成为生产者(Producer)，它们负责为整个种群寻找食物，并具有获取食物的优先权。生产者在每次迭代的过程中按下式进行位置更新：

(7)

式中：t为当前迭代次数，tmax为最大迭代次数；α为(0，1]之间的随机数；Q为一个服从正态分布的随机数；L为1×d维的单位矩阵；R∈[0,1]和ST∈[0.5,1]分别表示预警值和安全值。

种群中的其余个体被称为乞讨者(Scroungers)。当它们发现生产者寻找到新的食物时，将迅速飞往该位置并抢夺生产者的食物。其位置更新描述如下：

(8)

式中：Xp是目前发现者所占据的最优位置；Xworst则表示当前全局最差的位置；A表示一个1×d的矩阵，其中每个元素随机赋值为1或-1，并且有：

A+=AT(AAT)-1

(9)

i>n/2表示抢夺失败，不能获取到食物，此时该个体将随机飞往其他位置觅食；

同时种群中会有10%到20%的麻雀意识到有捕食者靠近的危险。哪些个体会意识到危险是一个随机过程：

(10)

SSA-ELM的总体流程如图2所示。

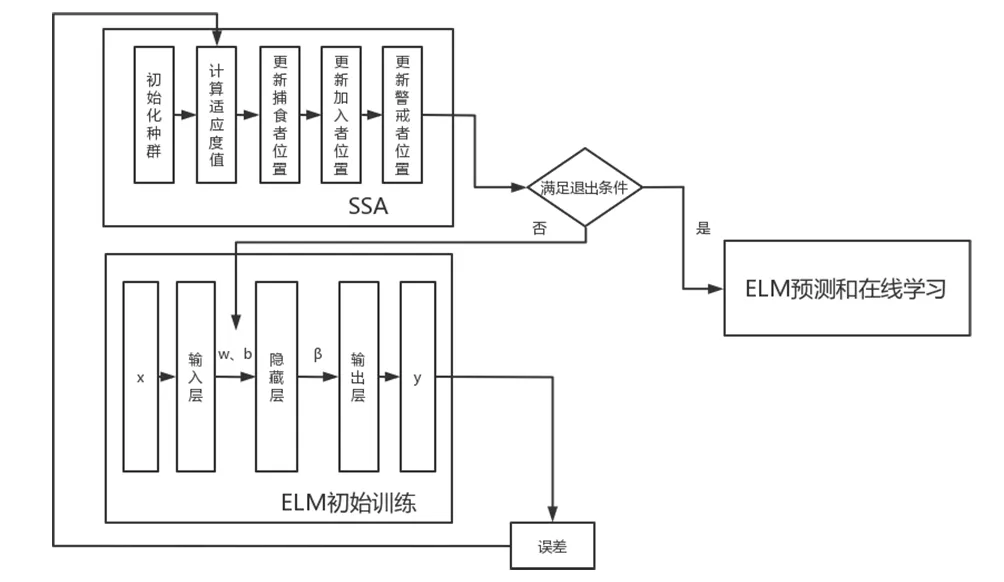
图2 SSA-ELM流程

2 MIT数据集上的模型验证

MIT数据集为Severson等[9]于2019年公开发表的锂电池循环充放电实验数据集。本文中选取数据集中2017-5-12批次数据中充电策略为3.6C(80%)～3.6C，采集通道编号1的实验数据，共包含1 189个循环、1 295 874条数据，其原始数据与经过突变点去除和低通滤波后的结果如图3所示。该数据中SOH变化趋势稳定，可直接进行时序预测。

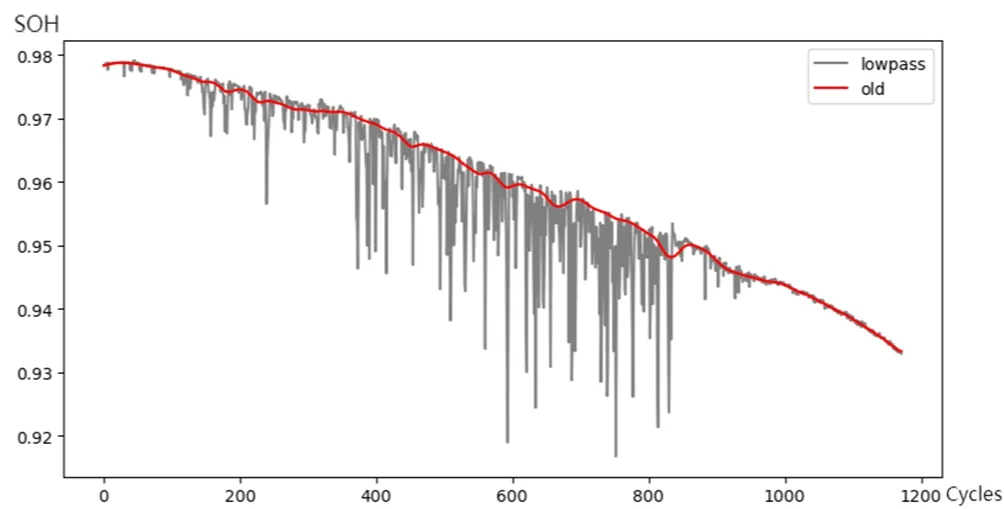
图3 MIT数据集SOH原始数据(灰色)及处理后结果(红色)

删去前60个SOH上升的循环后，将前400个循环作为训练集，其余作为测试集。模型用第a-6至a-1次充放电循环的电池SOH作为输入，第a次循环的电池SOH作为输出。在训练阶段，输入和输出中的SOH均采用真值。在预测阶段，采用相邻前5个循环的SOH预测值作为输入进行迭代式预测，同时使用在线学习更新模型提升在长期预测预测中的精度。预测结果如图4所示，均方误差为0.000 168，最大预测误差小于0.8%，具有很高的预测精度。接着在没有真值输入进行在线学习修正的情况下，继续向后预测未来100次循环的SOH容量变化情况(即第1 130次至1 230次循环)，结果基本准确地延续了之前的变化趋势。

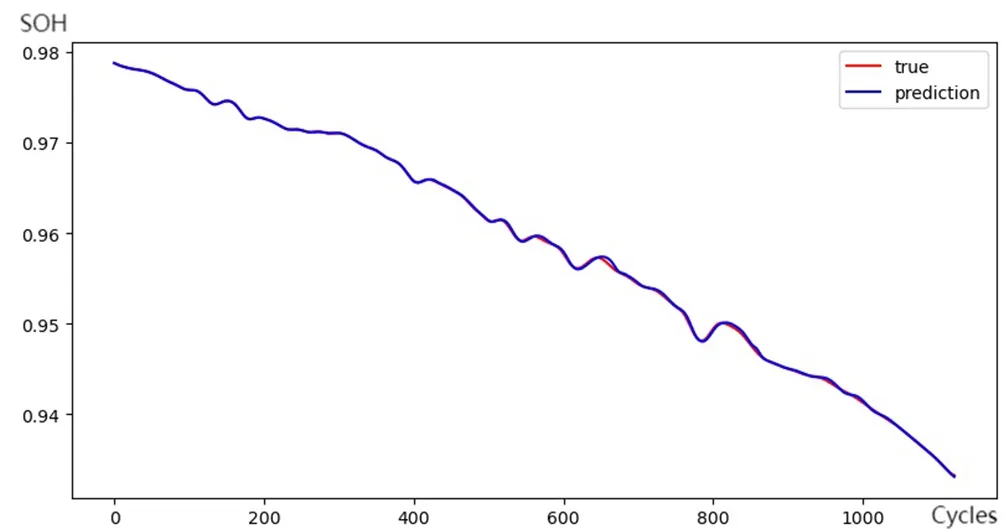
图4 MIT数据集SOH时序预测结果

之后，通过训练时间ttrain、多次训练平均均方误差RMSEMean、多次训练均方误差间的方差σRMSE三个指标对比了SSA-ELM和纯ELM性能，分别表征模型训练效率、预测精度和预测结果稳定性。结果如表1所示，SSA-ELM的精度和稳定性均明显优于纯ELM，训练时间增加但相比传统神经网络仍有较大优势。

表1 纯ELM模型与SSA-ELM模型性能对比

3 实车数据集上的模型验证

实车数据来源于新能源汽车溯源平台，车型为大众朗逸纯电动汽车。该数据集可提取542个有效循环的SOH，如图5所示，其噪声大，变化趋势不明显。

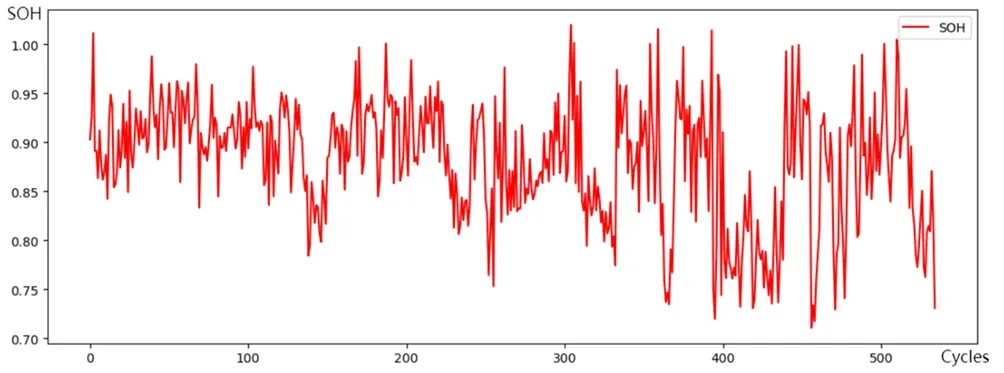
图5 实车数据集SOH

因此，采用两步式预测方法。第一步，用电池包总电压370 V升至400 V充电时间、历史累计平均充电电流和历史累计平均充电温度三个间接健康因子作为第一个模型的输入，对SOH进行建模。以前100个循环为训练集，其余为测试集，得到结果如图6所示。

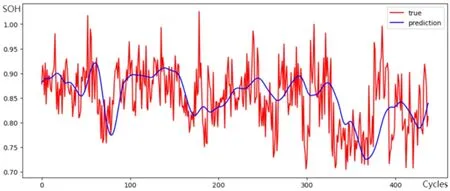
图6 实车数据集SOH建模结果

之后，将建模后的结果进行均值滤波以进一步减小波动，并输入到第二个时序预测模型中预测未来SOH变化趋势，结果如图7所示，预测的均方误差为0.002 58，最大误差为1.029e-2，相对误差小于1.25%，具有较高精度。

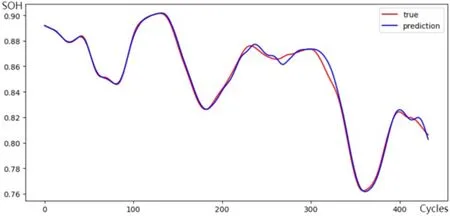
图7 实车数据集SOH时序预测结果

最后，将训练好的网络用于另一辆车的电池SOH预测以测试其泛化性能，结果如图8所示，均方误差为3.55e-3。预测效果在前半部分仍然较好，但后半部分精度下降，这主要是这部分样本变化趋势与训练集差别过大。总体上，仍可认为模型具有一定程度的泛化能力。

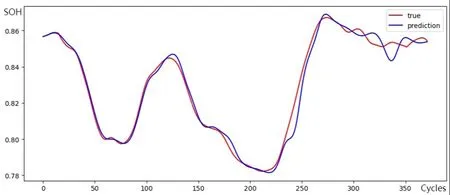
图8 泛化性能测试结果

4 结论

本文采用SSA算法优化的ELM预测电池SOH，解决了ELM隐含层参数随机赋值导致的预测结果不稳定问题，提升了最终的预测精度和稳定性。针对实车数据噪声大、变化趋势不明显的问题，采用两步式预测方法，先以特定电压区间充电时间、历史累计平均充电电流、历史累计平均充电温度三个间接健康因子对SOH进行建模，再进行时序预测，取得了较高的预测精度和一定的泛化能力。但研究工作中仍存在一些不足：如没有考虑行驶过程中数据的影响、缺少电池全寿命周期中的数据无法进行RUL预测等，可以在未来的研究中进一步补充。