小功率燃料电池动力系统设计及能量管理策略研究

于秋扬 庾昂

(上汽大众汽车有限公司，上海 201805)

0 引言

本文工作基于上汽大众的一个燃料电池开发项目。该研究仅处于起步阶段，公司主要关注小型燃料电池的复合电源系统的性能，因此选择了自行车这一低功率的用电装置为应用对象，最终设计出一款适用于自行车的燃料电池复合电源动力系统。

本文的研究意义在于：(1)完整地匹配了一套自行车用的燃料电池复合电源系统；(2)设计了合适的模型进行快速开发；(3)讨论了各能量控制策略的优缺点；(4)实物验证了功能和结构上的可行性；(5)为上汽大众后续的燃料电池样车开发项目提供了借鉴意义。

1 采用复合电源的燃料电池自行车动力系统集成设计

在工业领域，燃料电池复合电源在自行车领域鲜有研究。本文仿照现代汽车设计模块化、平台化的理念，将动力系统作为一独立的子模块进行研究，后将基础平台集成在整车中[1]。

如图1，总结下来，对于动力系统的集成主要可分为以下四个阶段的工作：

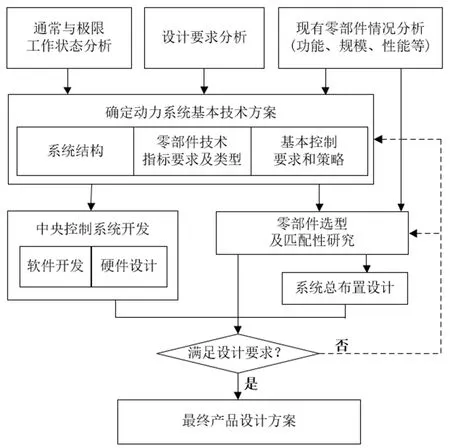
图1 燃料电池自行车动力系统集成设计流程示意图

(1)确定系统基本技术方案；

(2)分析、确定各零部件的性能指标要求及零部件类型；

(3)确定系统结构布置；

(4)分析系统需实现的基本控制功能并制定相应的控制策略。

1.1 整车受力分析图

首先，整车的受力分析如图2所示。根据经典动力学方程，在行驶过程中要克服坡度阻力[2]，空气阻力，滚动阻力和惯性阻力来驱动车辆，即为公式所示：

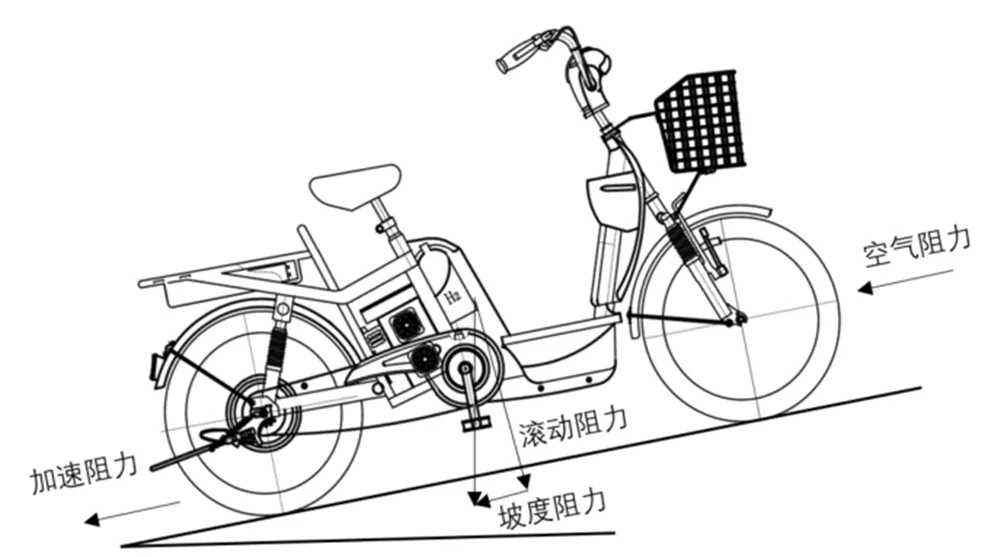
图2 整车受力示意图

Ft=Ff+Fi+Fw+Fj

(1)

随后展开为功率平衡公式，其中电机的输出功率等于各种阻力功率之和，如式(2)所示。

(2)

表1集中展示了该燃料电池自行车的整车参数，该参数根据国家标准制定[3]。

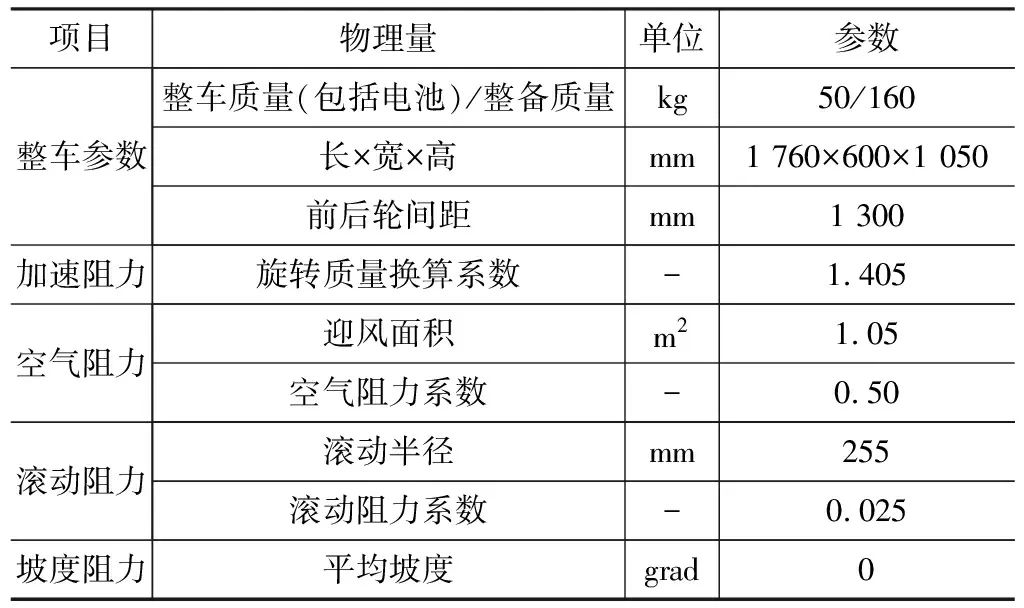
表1 整车参数一览表

1.2 燃料电池混动自行车路谱工况

目前针对电动自行车行业内并没有一个标准的测试路谱，仿照汽车行业路谱，对速度进行等比例地缩小至25 km/h之内, 并通过对整车的受力分析得出相应路谱的功率情况。

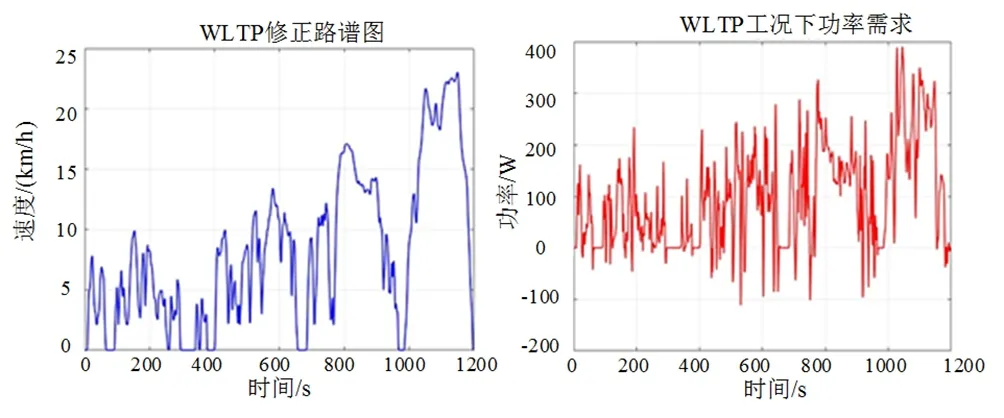
图4 WLTP修正路谱图

若功率不满足国标中对于电机功率的要求(电动机额定连续输出功率≤400 W), 则修改整车参数，如减少整车质量，优化迎风面积等，至满足国标对电机功率的要求为止。

本文将采用两种目前在汽车领域应用广泛行驶工况，分别为低速循环工况NEDC以及复杂变化路况WLTP，如图3与4所示。最终，两种工况的参数总结如表2所示。

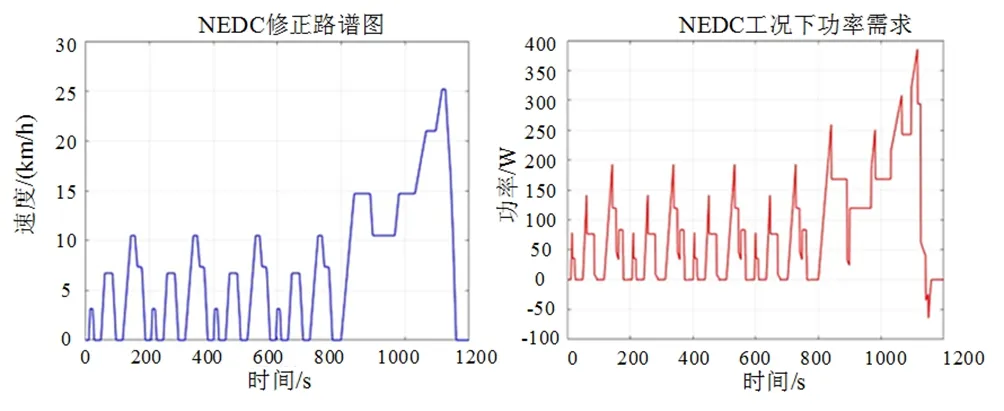
图3 NEDC修正路谱图

表2 两种工况参数总结

1.3 动力系统结构方案

由于燃料电池系统的输出电压会随输出功率波动，因此输出侧与一个单向DC/DC相连，从而将一个高内阻软特性电源转化为低内阻硬特性电源，输出电压得以稳定。本文在此基础上加入一能量分配单元，拓扑如图5所示。其中，该能量分配控制器可通过编程实现对充电电压，电流以及输入电流等进行数字化的精确控制。

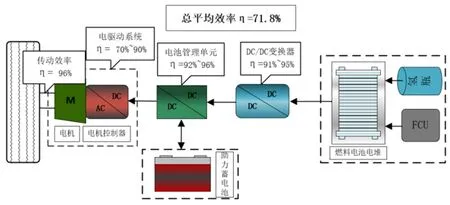
图5 动力系统的拓扑结构及系统效率

1.4 燃料电池功率范围选择

燃料电池和锂电池的选型和配比主要参考两项重要参数：

(1)表2中两种工况的平均功率；

(2)图3和4中动力系统的平均效率。

本文中燃料电池功率并不覆盖全部功率范围，只使其最佳工作点与循环工况下的平均功率保持一致。根据燃料电池以其最大功率的35%～50%为最佳输出功率的特性，故选取200 W的燃料电池，最佳工作点在100 W左右。

与此同时，因燃料电池可提供的最大功率大于在设定工况下电源应输出的平均功率，储能元件的容量也必然会得到平衡。且储能元件也没有必要选取过大的容量，其容量满极限情况下的放电需求即可。

1.5 零部件选型结果

本文所设计的电动自行车整体性能要求如表3所示：

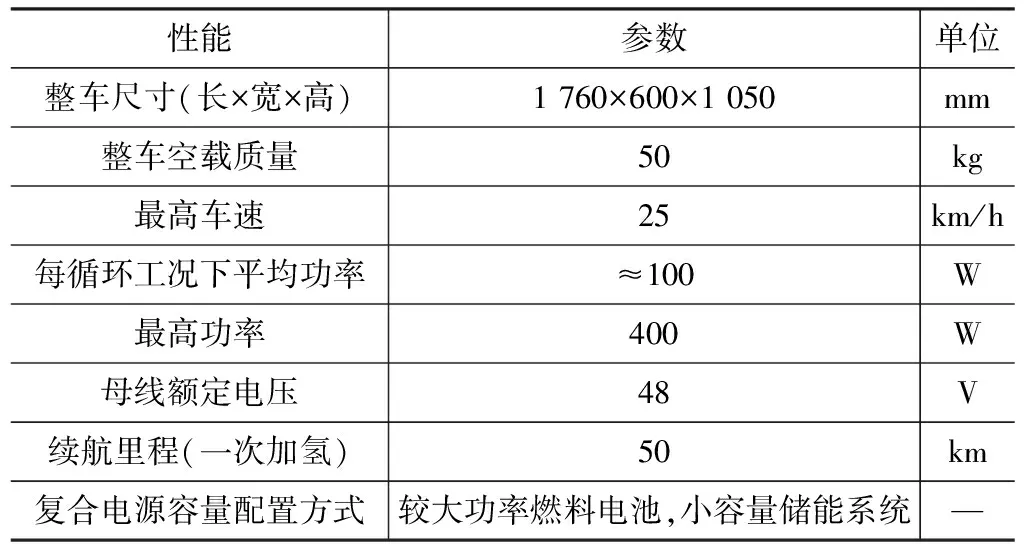
表3 电动自行车整体参数

根据表3中的该自行车需满足的性能参数以及本小结的选型理论，最终确定如表4所示的各零部件性能指标要求和具体类型。

表4 各零部件性能指标要求和具体类型

1.6 整车构造

在选定组成动力系统的零部件后，根据各零部件的外形尺寸、安装结构以及安装尺寸等与系统布置有关的信息和数据，借助于一定的CAD设计软件，可以很方便地完成动力系统的布置设计，如图6所示。

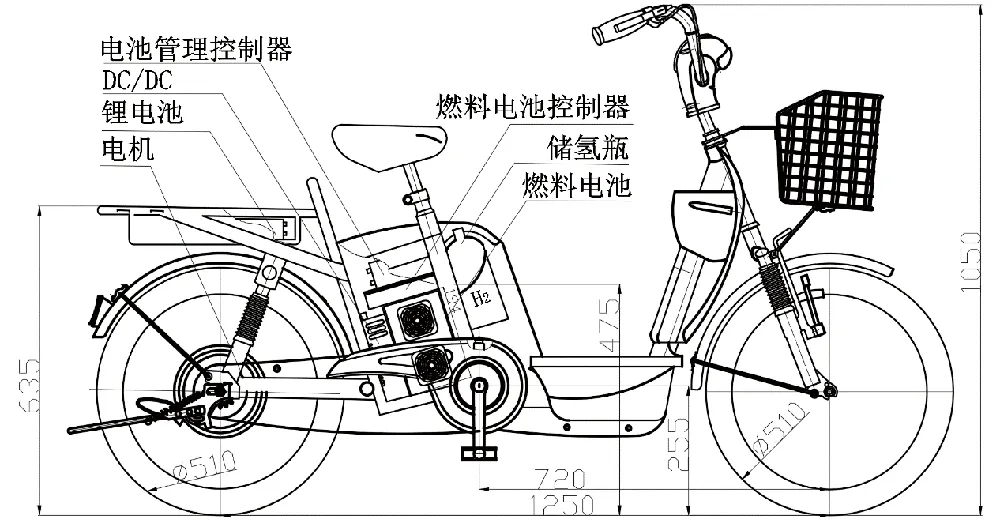
图6 燃料电池自行车整车与动力系统布局示意图

2 燃料电池复合电源动力系统建模

2.1 燃料电池

2.1.1 燃料电池模型

燃料电池可以被视为一个可控的电压源。由于存在三部分的损耗，其端电压会随输出电流的不同而发生变化。电堆输出电压可表示为公式3：

Vout=Vcell×Ncell=Enerst-Vact-Vohm-Vconc

(3)

其中，Ncell表示为电堆中电池片的数量。

(1)开路电压：没有外接负载情况下，存在理想的电压输出Enerst，也可称为开路电压。

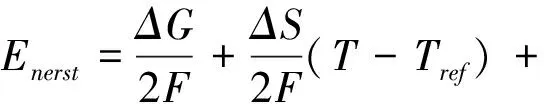
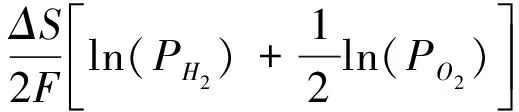
(4)

(2)活化极化电压损失：活化极化是由发生在电极表面、反应缓慢的动力学作用引起[4]。该电压损失的作用是在化学反应中驱使电子到达或者离开电极：

Vact=I×Ract=

β1+β2T+β3Tln(CO2)+β4Tln(I)

(5)

(3)欧姆极化电压损失：这部分损失是主要由质子膜的电阻，膜和电极之间的电阻以及电极本身的电阻所造成[5]。可表示为：

(6)

(4)浓度极化电压损失：浓度极化主要由于两个原因，造成化学反应不完全：(a)无法足够快地提供反应物；(b)无法足够快地清除产物[6]，可表示为：

(7)

2.1.2 燃料电池SIMULINK模型及仿真结果

SIMULINK模型如图7所示。根据H-200的数据表[7]与图8所示的实际数据进行比较，很显然，除了激活极化区域中的初始电压比实际情况略大以外，其余部分几乎相同。

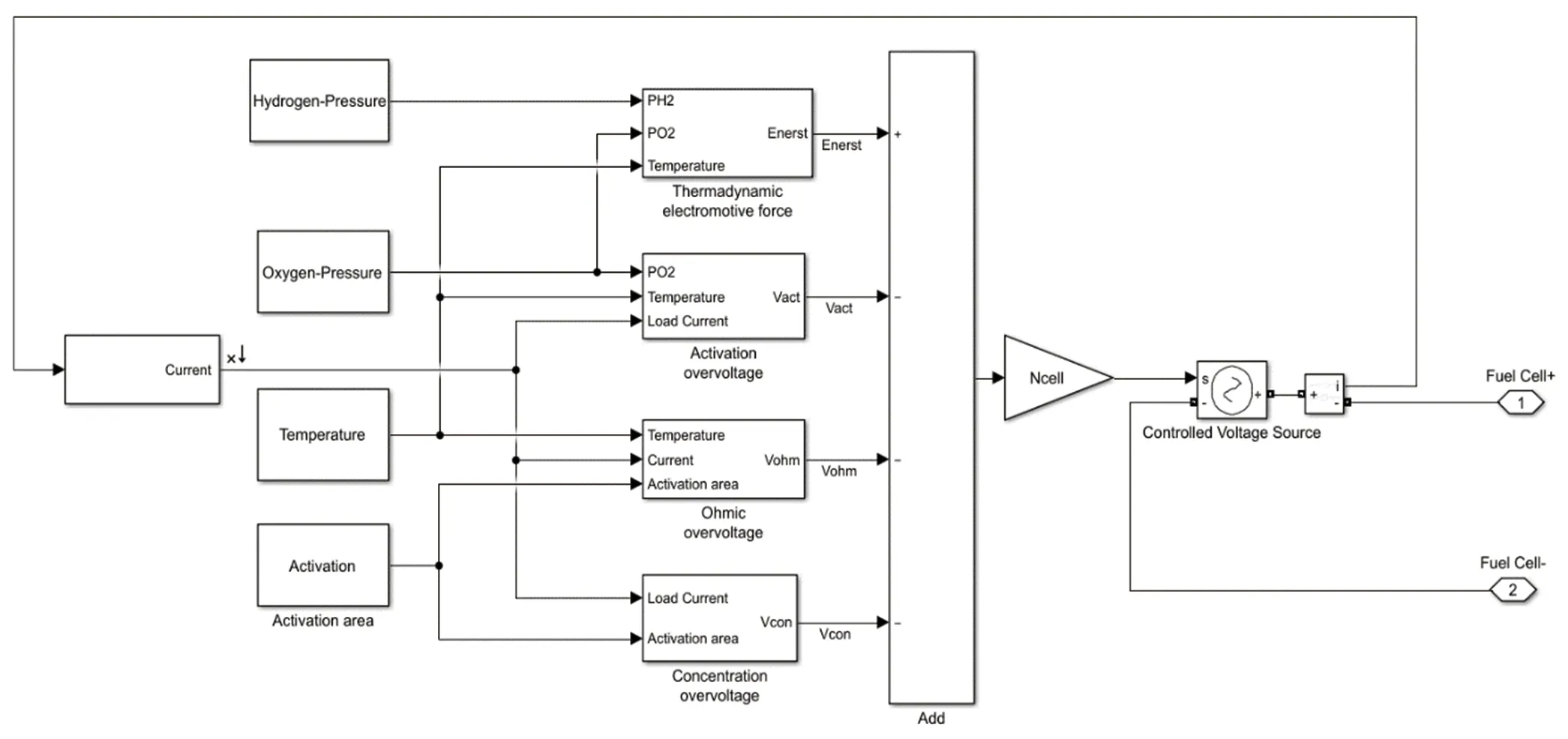
图7 燃料电池的Simulink模型

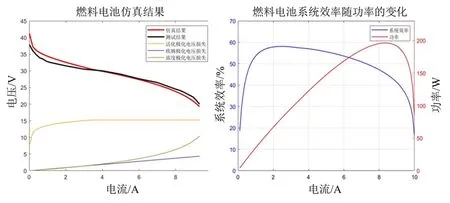
图8 燃料电池模型仿真结果与效率随功率变化曲线

2.2 蓄电池模型

本文采用rint模型进行蓄电池建模，电路原理如图9所示，其中Ebat为开路端电压，Ibat为蓄电池内部的电流，Rbat为蓄电池内部的等效电阻，Vbat为对外输出电压，关系如下式所示。

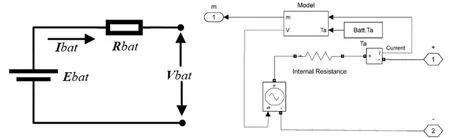
图9 蓄电池Rint与Simulink模型

Vbat=Ebat-Rbat·Ibat

(8)

其中，Ebat分为充电空载电压Ebatcha和放电空载电压Ebatdis，方程式如下：

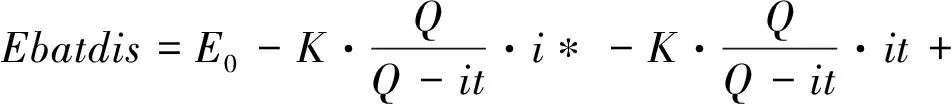
A·exp(-B·it)

(9)

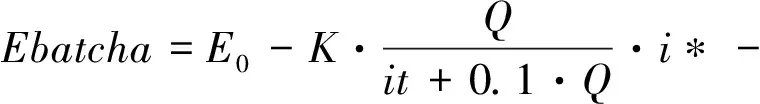
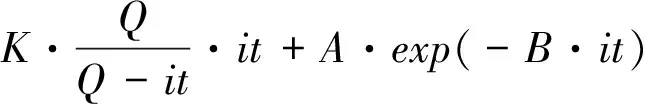
(10)

其中，Q是最大电池容量，it为电池的实际耗电容量，K为极化系数，A为指数放电区电压值，B为指数区时间常数倒数，i*为低通后的动态电流，i为实际电流。

锂电池的仿真结果和实际的测量结果对比如图10所示。

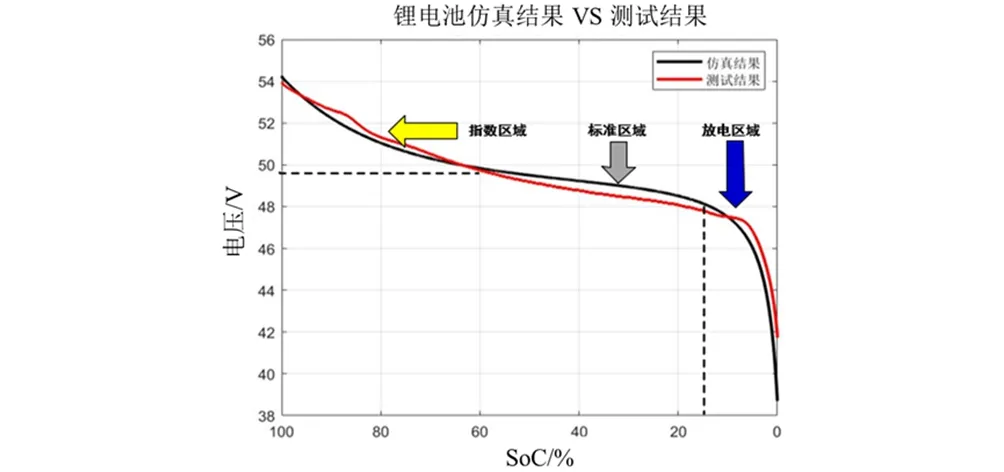
图10 锂电池仿真与测试结果对比图

2.3 DC/DC模型

2.3.1 变换器的模型分析

本文采用了基于状态空间平均法建立的DC/DC平均值模型。该方法利用电路的等效变换，将开关器件隔离，构成一二端口子网络，然后分别对端口电流、电压在开关通断的两种状态下进行计算。最后将电路等效为受控电流源与受控电压源[8]。等效电路图如11所示。

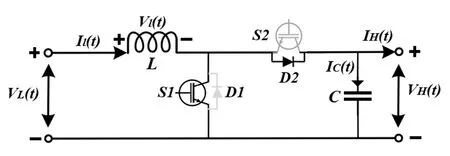
图11 Boost变换器等效电路

在Boost模式下，开关S1将周期性地打开和关闭，开关S2则始终打开。当开关S1导通时，系统的状态方程为[9]：

(11)

当变换器满足低频假设与小纹波假设时，可以认为一个开关周期内状态变量的瞬时值近似等于它的周期平均值[10]，即VH(t)≈〈VH(t)〉,Il(t)≈〈Il(t)〉。以d(t)代替D，则合并之后可得升压模式下的平均值模型。

(12)

需要注意的是，在该模式下，能量为单向流动，电流极性不能发生变化[11]。结合平均状态方程，升压模式下的平均值电路模型对应的受控源等效电路如图12所示。

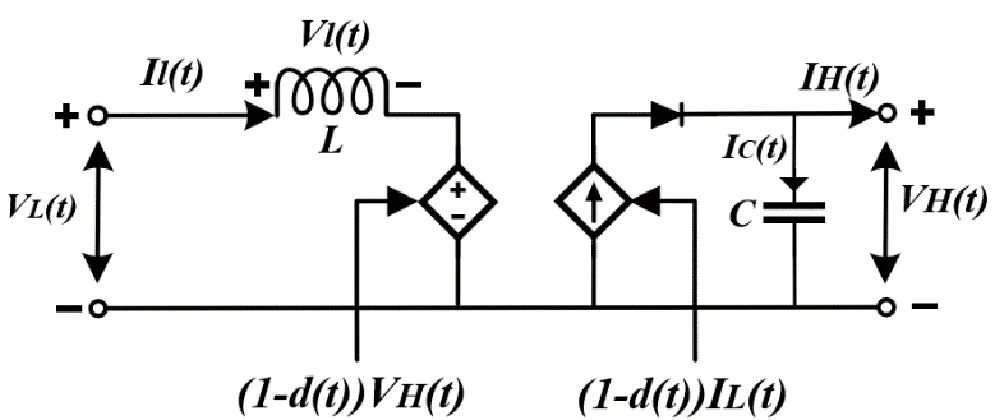
图12 平均电路模型等效电路

2.3.2 Boost变换器控制器设计

在Boost变换器控制器的设计过程当中，为了加快系统的响应速度，控制器采用内环控制为电感电流闭环、外环为电压闭环控制的双闭环控制结构，且电流环与电压环均采用PI控制器，控制器的控制信号流程图如图13所示。

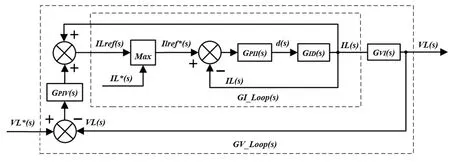
图13 Boost控制器的控制信号流程图

其中，GID(s)为电流环被控对象的传递函数，GVI(s)为电压环被控对象的传递函数，GPII(s)与GPIV(s)分别为电流环和电压环的PI控制器传递函数。

图14则为DC/DC变换器的平均模型。绿色部分为信号的当前值，即输入和输出端的电压电流；最后的红色部分即为经过调整后该时刻下的电压值和电流值。

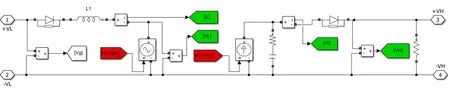
图14 DC/DC变换器Simulink模型

在建模层面即把电池管理单元忽略不计。但是其效率损耗仍然是需要考虑的，图15中所示的则是DC/DC和电池管理单元的效率随功率的曲线。本文在效率上将两者的损耗合二为一，最终的结果如右侧图所示，建模时也将该损耗计算在内。

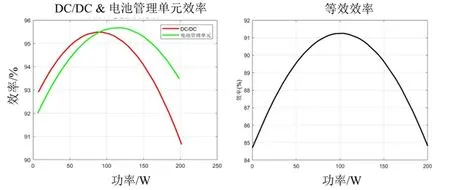
图15 DC/DC与电池管理控制器效率曲线图

2.4 电机与驱动控制系统模型

本文将电机控制器+电机+传动部分等效为一个黑箱结构，如图16所示。其中，在已知电机转速以及转矩的需求下，通过电机map图可求出电机效率，再考虑到电机到车轮的传递效率，可以计算出电机与驱动控制系统最终的功率需求。

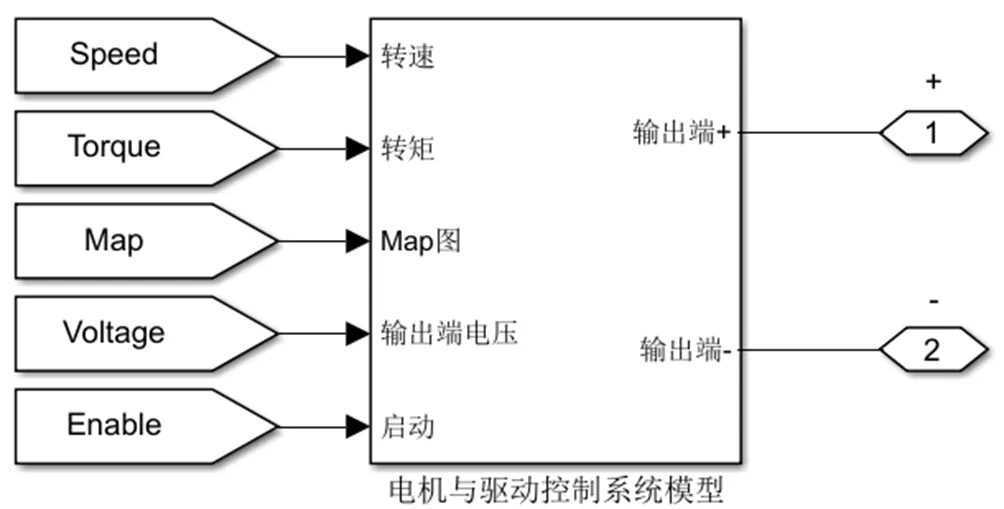
图16 电机与驱动控制系统模型

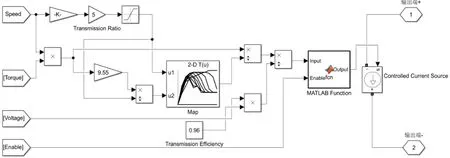
图17 电源系统实际消耗功率计算流程图

为了简化模型和加快仿真速度，可用一个可控的电流源作为负载实现建模目的。可控电流源的当前电流由电机与驱动控制系统的整体功率需求和当前母线的电压值决定。其中Enable为电机的使能信号，该信号由能量管理系统(EMS)给出。

如图18所示，该图为额定功率350 W，最大效率转速为1 350 r/min的轮毂电机的Map图。由该图可以在已知电机转速和电机输出功率的前提下，通过对应的转速和转矩(这里将输入转矩近似为输出转矩)反推得到电机的输入功率。

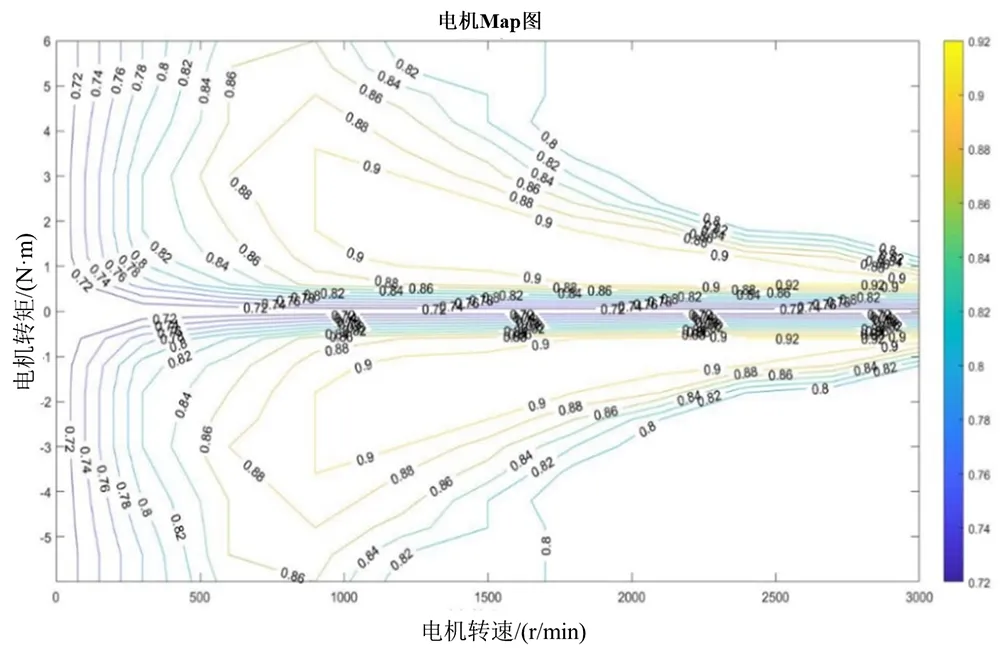
图18 电机Map图

2.5 SIMULINK总体模型

将燃料电池，锂电池，DC/DC以及负载的独立模型设计完毕之后，则将它们按照实际的拓扑结构进行连接，如图19所示。同时，在该离线仿真模型中加入对各模块的电流电压传感器，将信号传输给计算模块进行统一的功率、氢气消耗、效率、SOC等变量的计算；能量管理模块将对DC/DC的输入电流进行控制，控制策略将在下一章节进行讨论。

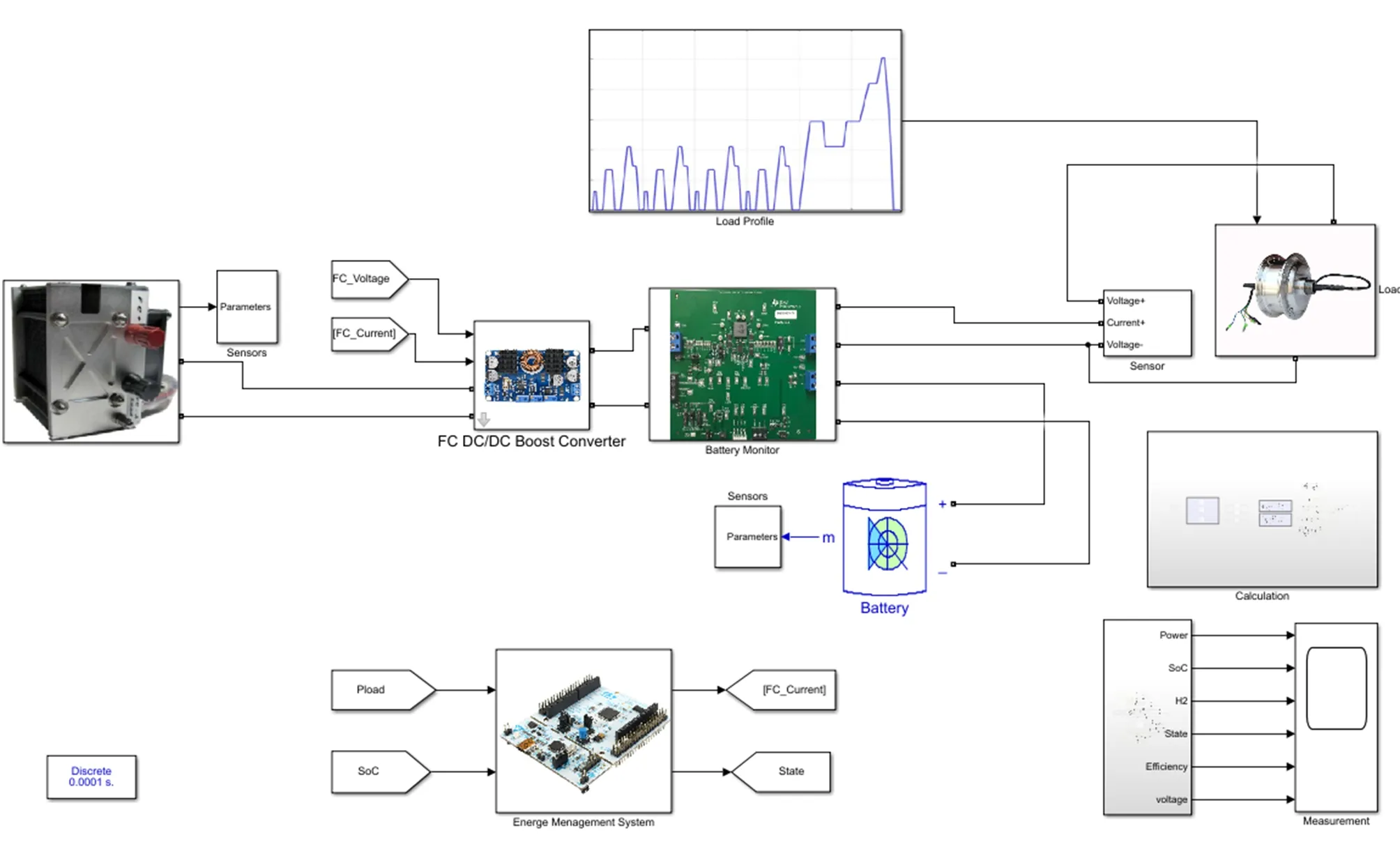
图19 系统总Simulink模型

<下一期待续>