超宽幅遥感转扫成像分析

谢虹波，费 强，谢新旺，孙景旭

（季华实验室，广东 佛山 528200）

1 引 言

近年来，随着光电成像技术的进步，国防、林木业等领域对遥感图像的高空间分辨率、低成本以及高时效性等需求逐步提升，发展轻量化、大幅宽、高性能成像卫星及其星座等逐渐成为主流趋势［1-2］。国外遥感相机的发展已逐步完成从时间延时积分（TDI）CCD［3］到CMOS图像传感器的转变，采用CMOS图像传感器既可以实现推扫成像，也可以实现面阵成像，而且大幅度地降低了研制成本和研制周期，且采用CMOS工艺可以很容易和后端的一些数字电路实现单芯片集成，使得航天遥感相机更智能。目前基于CMOS工艺的遥感相机主要分为线阵TDICMOS探测器和面阵CMOS探测器。面阵CMOS探测器可以实现视频成像，且具有更高的动态范围，但是需要配合像移补偿等运用机构；而TDI型的探测器配合运用机构可以实现更大幅宽的成像，更多地被运用在大幅宽推扫成像，通过多片拼接可以实现更宽的幅宽。遥感相机发展的主要方向之一是在保证分辨率的情况下尽可能地扩大幅宽。已有的TDI推扫成像线阵方向都是垂直于飞行方向，在垂轨方向的幅宽依靠探测器的像元数决定，可通过在垂轨方向的多片拼接实现更大的垂轨幅宽，沿轨方向通过卫星飞行速度与行频匹配实现理论上的连续推扫。已有的沿轨推扫方案是目前运用最多的利用卫星的姿轨控以及卫星飞行实现沿轨的大幅宽推扫成像，在垂轨方向采用多片拼接增大幅宽，从而实现对地大面积推扫成像。吉林一号卫星通过垂轨6片探测器拼接实现了136 km、0.75 m的幅宽［4］。沿轨推扫方案利用卫星本身的姿轨控机构和卫星固有飞行属性实现了推扫，不需要额外的运动机构，大幅简化了相机载荷的整体设计，但是垂轨方向上多片拼接方案会增加系统的成本及装调难度。多片拼接需要更大的焦面，大焦面需要进一步增大光机结构的F数，这导致光机结构整体尺寸偏大，光路设计难度更高，这违背了商业航天低成本、小型化、轻量化的初衷。采用垂轨环扫式的光学遥感卫星通过沿轨拼接、垂轨环扫成像方式兼顾了超大幅宽和高分辨率特点，但是已有的垂轨环扫式成像是利用卫星的机动特性实现的，对卫星的敏捷性和机动能力提出了新的挑战［5］。

为了满足商业航天的小型化、低成本需求，本文提出了采用反射镜在垂轨方向转扫扫描的方案，可以实现垂轨方向大幅宽成像。相比于以往多片拼接方案，该方案减小了焦面，可以采用小F光机设计，有效减小相机整体尺寸和重量，大幅降低成本。本文中阐述的转扫方案实现了在垂轨方向幅宽达到千公里量级，在沿轨方向上通过卫星飞行实现连续成像，最终形成千公里级宽度的连续转扫成像。

2 成像模型

本系统为垂轨转扫成像系统，转扫方向垂直于卫星飞行方向。转扫机构采用旋转反射镜，通过两面镀膜达到两面均可反射的效果，这里简称两面镜。

广域相机成像光路示意图如图1所示，成像区域对应大小为E的物体发出的光到达反射镜，经反射后的光到达离轴三反透镜［6-7］，再经过后光路最终到达焦面上。这里把离轴三反透镜及后光路部分统称为聚焦镜组。假定成像区域为E的物体，对应焦面上的光斑大小为δE，遥感相机物距可以近似等效为轨道高度H，可以得出成像公式如式（1）所示：

图1 成像光学装置示意图Fig.1 Diagram of imaging optical system

式中，f为成像系统等效焦距。当δE探测器的最小像元尺寸为d时，此时对应的E即为地面分辨率（D）。

2.1 行频匹配

转扫成像系统中一个重要的方面是行频匹配［8-10］，即下一行像元曝光时与上一行像元曝光对应地面相同的成像区域，通过控制转镜转速和探测器曝光时间使两者刚好匹配。行频匹配的精度在一定程度上影响了成像的质量。图1中两面镜匀速转动，转轴垂直于纸面，与飞行方向平行，即两面镜扫摆方向与飞行方向垂直，通过两面镜的转动，可以实现垂轨的宽幅成像。在沿轨方向通过控制扫摆周期使得前后两次扫摆图重合可以实现沿轨连续成像。

考虑沿轨方向相邻两次转扫的图像重叠，设重叠比例为p，两面镜转动成像的单面可成像摆角为θ（由于两面镜转动对应入射光法线转动，因此光学视场成像角度为2θ）。两面镜属于两面反射，因此每180°（π）为一个成像周期。轨道高度为H，根据万有引力公式可以计算出卫星对应的飞行速度v：

其中r=R+H，R为地球半径，ME为地球质量，万有引力常量G为6.67×10-11N·m2/kg2。

单幅沿轨方向的幅宽与设计指标相关，最终与选用的探测器相关。这里假定L为沿轨方向成像区域的幅宽，探测器在沿轨方向的总像素为N，则L=D×N，D为地面分辨率。

考虑前后图像重叠比例p，则可以计算出单幅图像所占的最大时间T为

2.2 分辨率及幅宽

由于地球是一个球体，当转镜转到不同的角度时，物距S其实是变化的，角度越大则物距变化越明显，这也就对应地球上的分辨率变化。图2为扫描成像模型。

图2 扫描成像模型Fig.2 Model of scanning image

这里假定对应星下点时，转镜角度对应绝对零点。当光轴转到α角时，此时对应地球上的P点，P点与地心连线与相机与地心连线之间夹角为β，根据几何关系可以计算出β：

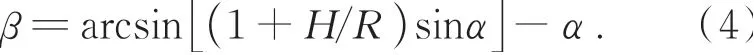
由于探测器最小像元为d，光学系统的角度分辨率为

因此α角的最小改变量为δ，此时对应的地面分辨率Δx为

因此角度α处对应的分辨率为其中R为地球半径，H为轨道高度，f为光学系统等效焦距，α为光轴的角度。

垂轨方向的转扫幅宽W为

总的幅宽为L×W，对应的像素数为N×M。

在实际运用过程中，由于地球自转的影响，实际地面物体像移速度是多个速度的合成，存在一个偏流角［11-12］，如图3所示，vs为卫星相对地心的飞行速度；vm为沿飞行方向的地移速度，vm=为地球自转速度；θ为卫星轨道平面的倾角；vp为合成速度，φ为偏流角，通过几何计算可以得到合成速度以及偏流角。为了实现更好效果的成像效果，最好保证转扫方向与合成速度方向正交。

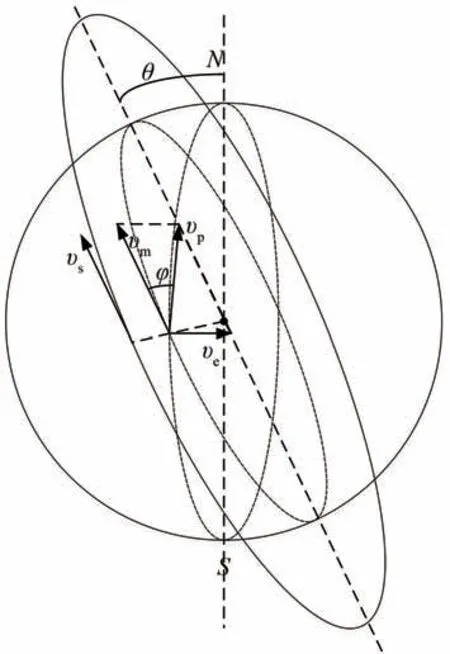
图3 偏流角Fig.3 Drifting angle

3 成像系统参数分析

以成熟的太阳同步轨道来分析，系统中的一些参数如表1所示。对应轨道高度为600 km时，对应的卫星飞行速度vs为7.56 km/s，对应的地移速度vm为6.91 km/s，星下点分辨率D为4.8 m，沿轨幅宽L为118 km，转镜转动180°对应时间T为14.023 s，有效成像时间t为3.355 s，转镜角速度ω为12.82°/s，像元对应的角分辨率δ为8 urad，成像范围2α为±43°，垂轨方向总行数M为187.623 K，垂轨方向幅宽为1 171 km，行频为55.93 kHz。当像素深度为10 bit时，对应的峰值数据率为12.8 Gbps。

表1 成像系统中的参数值Tab.1 Parameters of imaging system

前面定义，当光轴对着星下点时，对应地面分辨率最高。当转镜转动到最大摆角时，此时对应地面的分辨率最低，分辨率从4.8 m变到10 m。图4是分辨率随着转镜摆角的变化关系。

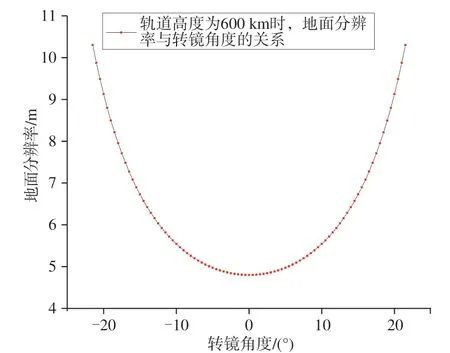
图4 分辨率与转角的关系Fig.4 Relationship between the resolution and rotating degree

卫星在轨运行时由于多方面原因，轨道高度会发生变化。轨道高度的变化会影响成像系统的多个指标。这里假定光学系统参数不变，焦距f、重叠部分比例因子p、像元尺寸d、摆角范围α、沿轨总的像素数N不变。

轨道高度H从600 km变 到440 km时，分辨率与轨道高度的关系如图5所示。对应星下点，当轨道高度从600 km变到440 km时，分辨率从4.8 m变到3.52 m，分辨率与轨道高度是反相关关系。

图5 不同轨道高度下的分辨率与转角的关系Fig.5 Relationship between the resolution and rotating degree with different heights

图6是轨道变化时成像幅宽与轨道高度的变化关系。可以看到高度为600 km时，转扫幅宽可以达到1 170 km。当轨道高度变为440 km时，转扫幅宽为848 km。

图6 转扫幅宽与轨道高度的关系Fig.6 Relationship between the scanning width and orbital height

为了保证相邻两次转扫图片存在10%重叠，转镜转扫180°的周期会随着轨道变化，图7是转镜转扫180°的周期与轨道高度的关系。为了满足重叠比例因子p不变，当轨道变高时，转镜的转扫周期变大，高度为600 km时，转扫周期T为14.04 s，有效成像时间t为3.35 s。

图7 重叠比例因子p为10%时，转镜转扫180°周期与轨道高度的关系。Fig.7 Relationship between the time of rotating 180° and orbital height with 10% overlap

图8表明重叠比例因子p不变时，转扫行频与轨道高度成反相关关系。高度越低，行频越大，总的数据率越大。

图8 重叠比例因子p为10%时，转扫行频与轨道高度的关系。Fig.8 Relationship between the scanning line frequency and orbital height with 10% overlap

4 结 论

文中针对超宽幅转扫成像系统进行了分析，重点讨论了轨道变化对成像的影响。在实际工程化过程中有几个方面需要进一步考虑和优化。首先，由于偏流角的存在导致最终的转扫图像是一个平行四边形，在实际工程运用中为了更好地实现TDI成像，可以适当调节卫星的姿态，减小偏流角的影响。另外在轨道高度不变情况下，成像分辨率随转镜角度改变而变化，角度越大，分辨率越低，星下点对应的分辨率最高，这会导致最终的图像在转扫方向存在图像比例不一致，越靠近图像边沿，图像畸变的越明显，这个现象可以通过后期图像处理来优化。

本文针对采用二面镜进行转扫光学成像的遥感相机进行了一些系统分析，从航天运用的角度分析各个指标对成像系统的影响，重点分析讨论了变轨对成像系统的影响，从分辨率、成像幅宽、转扫周期及行频等角度分析轨道高度的影响。轨道越高，分辨率越低，成像幅宽越大，在保证相邻转扫图像重叠比例因子不变情况下，渡越时间越大，行频越低，对后端读出系统设计要求越低；轨道越低，分辨率越高，成像幅宽越小，在保证相邻转扫图像重叠比例因子不变情况下，渡越时间越小，行频越高，对后端读出系统设计要求越高。本文中涉及的光学系统可实现垂轨方向千公里级的遥感成像，沿轨方向可连续成像，在遥感成像方面具有很大的实用价值，在实际工程运用中，应该综合考虑，依据本文中的模型和分析结果，结合具体的使用环境，优化系统设计，使其具有一定的鲁棒性。