三基色显示中白点坐标对立体色域的影响及其准确计算

王 贯，顾 春*，许立新

（1.中国科学技术大学 核探测与核电子学国家重点实验室，安徽 合肥 230026；2.中国科学技术大学 安徽省光电子科学与技术重点实验室，安徽 合肥 230026；3.中国科学技术大学 安徽省先进激光技术实验室，安徽 合肥 230026）

1 引 言

高清、全色、三维是显示系统目前的发展方向。各种新型光源如量子点［1］、OLED［2］、激光［3-4］等光源成为了新一代显示光源的领跑者。色域是显示系统的一个重要指标，它表示了显示系统显示颜色的能力，在新一代的显示标准如Rec.2020［5］、DCI-P3［6］中，都明确包含了其中的色域标准。不同的光源拥有不同的中心波长和光谱宽度，研究这些参数对色域的影响很有意义。描述色域的方案主要有两种：基于CIEXYZ色空间的平面色品图和基于CIELAB色空间的立体色品图。前者不够均匀，并且不能表示显示系统亮度对色域的影响［7-9］，因此研究者主要采用立体色品图描述色域，即立体色域。Masaoka等人研究了大色域三基色电视的波长选择［10］。Song等人从色域覆盖率出发，研究了多基色激光显示的波长选择［8］。基于Macadam理论，我们研究了三基色激光显示中心波长和光谱宽度对立体色域的影响［11-12］。然而在不同的标准中，白平衡点的选取通常是不同的，如在Rec.709和Rec.2020的标准 中，白 平 衡 点 通 常 选 取 为D65［5，13］；而DCI-P3标准的白平衡点则为（0.314，0.351）［6］；在IEC 62977-2-1：2021这一标准中，白平衡点则选取了D50［14］。

白点色坐标是显示系统的重要参数，通过改变显示系统基色强度配比，可以改变白点色坐标。白点色坐标不同，观察者的观看感受也不同。在显示设备的实际使用中，由于光源、光学器件、照明条件等个体差异，每种光源的光学参数都会有微小的不同，为了达到符合标准的白点色坐标，常见的配平方案有两种：

（1）按照相同的强度配比进行配平，结果是光学参数的差异会导致白点的移动。

（2）保证白平衡点坐标不变进行配平，这样会增加实际操作中的工作量。

两种方案在实际生产中都可能存在，因此，十分有必要研究两种方案下各种光学参数对显示系统色域的影响。这样，必须综合考虑显示系统参数、白点坐标以及立体色域等问题。

本文在考虑白点色坐标变化的前提下，研究三基色显示系统中心波长和光谱宽度对显示系统立体色域的影响，并将立体色域影响分为两个部分：参数影响带来的直接部分和白点坐标影响带来的间接部分。利用这一算法可以计算出两种方案下显示系统参数对立体色域的影响。指导两种方案中显示系统的参数选择。

2 白点色坐标影响的理论模型

2.1 显示系统各参数之间的关系求解

设三基色显示系统3个基色强度为ER、EG、EB，对 应 的 三 刺 激 值 分 别 为(XR，YR，ZR)、(XG，YG，ZG)、(XB，YB，ZB)，白点色坐标为(x0，y0)，它们应该满足关系：

其中，R、G、B分别表示红光、绿光和蓝光，S表示比例系数。

计算基色的三刺激值可以通过式（2）～（4）导出，以计算红光的三刺激值为例：

设λR为红光的中心波长，ΔλR为红光的光谱宽度，一般的光源光谱强度分布满足高斯分布，即

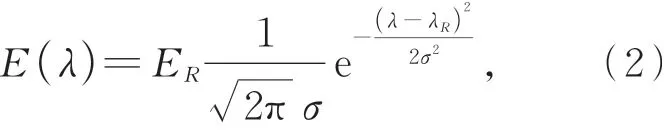
其中，

那么可以得到红光的三刺激值分别为

绿光和蓝光的三刺激值计算同红光类似。

结合式（1）～（4）可以看出，当三基色的中心波长和光谱宽度被给定时，作为齐次方程的式（1）可以解出三基色的比值。在三基色显示系统中，白点色坐标和三基色强度比值不是独立的。它们中的一个可以通过另一个解出。

2.2 三基色显示系统立体色域的影响参数

根据参考文献［8］中结论可知，光源基色波长和基色亮度可以影响显示系统的立体色域，而参考文献［10，12］中的结论告诉我们，光源的光谱宽度也影响显示系统的立体色域，而这些参数又根据白平衡点坐标通过公式（1）来配平。我们将以上影响三基色显示系统立体色域的参数总结为：

（1）三基色的中心波长λR、λG、λB；

（2）三基色的光谱宽度ΔλR、ΔλG、ΔλB；

（3）三基色的基色强度ER、EG、EB；

（4）白点色坐标(x0，y0)。

根据2.1的结论，当式（1）和式（2）已知时，式（3）和式（4）的其中一个可以被另一个解出来。因此，三基色显示系统立体色域的体积可以被三基色的中心波长、光谱宽度和白点色坐标决定下来。设V为三基色立体色域的体积，有

在显示系统中，每个基色的中心波长和光谱宽度和光源光学性质有关，它们彼此是独立的，当讨论基色的立体色域同某一参数的关系时，假设在三基色光谱宽度相同（ΔλR=ΔλG=ΔλB=Δλ）的情况下，光谱宽度对立体色域的影响的表达式为

讨论谱宽的影响时，显示系统的波长不会发生变化，式（6）可以被简化为

3 光谱宽度对立体色域的影响

以计算波长符合Rec.2020标准的光源光谱宽度随色域影响为例，首先计算Δx0和Δy0，光源的三基色波长为

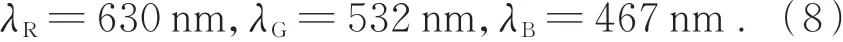
当三基色光谱宽度为1 nm，白点坐标为D65（x0=0.312 7，y0=0.329 0）时，根据式（1）～（4），其三基色强度比值为

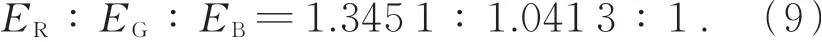
可以计算白点色坐标的偏移量Δx0和Δy0的公式分别为

其中：

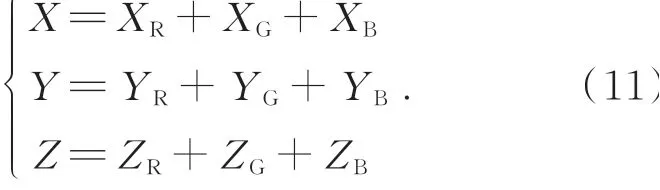
将光谱宽度从1 nm逐渐展宽到60 nm，计算其白平衡点的偏移如图1所示。

图1 白点坐标随着三基色光谱宽度的变化Fig.1 Relationship between the white point coordinates and the spectral width of the three primary colors

接下来使用公式（1）～（4），改变白点色坐标并计算色域体积，图2表示了当三基色波长为630，532，467 nm时，色域体积随着白点色坐标变化的关系。

图2 色域体积随着白点色坐标的变化（a）及白光在CIEXYZ色品图中的位置（b）Fig.2 Color gamut volume changed with white point color coordinates（a）and the position of white point in the CIEXYZ chromaticity diagram（b）

在前面的研究中，我们分别计算了不同光谱宽度下三基色显示系统的色域体积。在求解的过程中，我们忽略了光谱宽度改变对白点色坐标的影响［11-12］，按照式（6），白点坐标修正前后的立体色域和光谱宽度对应关系如表1所示。在计算过程中设 定 为 式（13）中 的常数。

计算其他光谱宽度时，三基色强度配比保持式（9）不变，这样会使得白点色坐标和D65之间产生一定的差距，如果此时想要得到白点色坐标在D65的立体色域，就要根据式（7）进行修正。结果显示，两种算法计算出来的结果非常吻合，可以认为这种算法能够模拟白点色坐标对立体色域的影响。

图3 色域体积对白点横坐标的偏导数（a）和纵坐标的偏导数（b）Fig.3 Partial derivative of the gamut volume with respect to the abscissa of the white point（a）and the ordinate（b）

表1中的结果显示，在光谱宽度展宽为20 nm时，白点色坐标的偏移小于0.01。所以，在之前讨论光谱宽度对立体色域的影响时，我们往往会忽略白点坐标偏移对整体色域的变化。通过上面的计算结果，能够得到考虑到白点偏移情况下的立体色域随光谱宽度的变化趋势。根据公式（7），可以把立体色域的变化分为两个部分：

表1 白点坐标修正前后的立体色域和光谱宽度对应关系Tab.1 Relationship between stereoscopic color gamut and spectral width before and after white point coordinate correction

4 其他参数对立体色域的影响

4.1 单一基色谱宽对立体色域的影响

保持三基色波长选取为λR=630 nm，λG=532 nm，λB=467 nm，分别将红、绿、蓝三基色光谱宽度从1 nm逐渐展宽到60 nm，在两种情况下，计算它们的立体色域随谱宽增加的变化，结果如图4所示。

图4 两种假设下光谱宽度和立体色域之间的关系Fig.4 Relationship between spectral width and color gamut under the two assumptions

根据文献［12］，三基色光谱宽度对立体色域的影响为绿色≫红色＞蓝色，这符合白点固定方案的结果。然而，在考虑显示系统强度配比一致这个假设时，3个基色光谱宽度对色域的影响相当，这种现象的主要原因可以用图1来解释。增加绿光光谱宽度时，白点色坐标的x值增加而y值减少，尽管直接部分是负值，根据式（6）和式（10）得到的间接部分却是正值，两个部分互相抵消从而减弱了绿光谱宽增加对立体色域的影响。对于另两个基色而言，在光谱宽度增加的过程中，间接部分都是负数，这使光谱宽度对色域的影响得到了增强。

4.2 波长选择对立体色域的影响

与光谱宽度一样，光源波长也是显示系统的重要参数。根据4.1节以及参考文献［12］，显示系统中绿光对显示系统的影响最大。在色域方面，评价一种波长对色域的影响主要从两个方面进行：（1）立体色域的最大值；（2）立体色域随着光谱宽度的增加减少的幅度。

在显示系统中，绿光的主要波长有520，525，532，550 nm等。选择绿光波长时，我们保持λR=630 nm和λB=467 nm不变。

计算过程和第3节类似，首先计算白点色坐标的偏移Δx0和Δy0，结果如图5所示。

需要注意的是，尽管色域体积对白点坐标的偏导看起来非常大，甚至超过了立体色域本身（2×106左右），但是根据图5，白点坐标的偏差仅为10-2量级，导致色域体积差距大约仅为104～105这个量级。不同绿光波长下的色域体积对白点坐标的偏导如表2所示。

图5 不同绿光波长下白点坐标与光谱宽度的关系Fig.5 Relationship between the change of white point coordinates and the spectral width of the green primary

表2 不同绿光波长下的色域体积对白点坐标的偏导Tab.2 Deviation of the color gamut volume to the coordinates of the white point under different wavelengths of green light

获得这两个参数后，根据公式（7），计算不同中心波长绿光在两种配平方案下的立体色域变化，结果如图6所示。结果显示，在两种方案下，绿光中心波长和光谱宽度对色域体积影响的趋势是一致的：波长520 nm的绿光在窄光谱下色域体积最大，并且随着谱宽增加色域体积衰减也最明显，与参考文献［12］的结果相符。我们认为，两种方案结果相近的原因为随着光谱宽度的增加，不同波长的绿光引起的白点坐标移动较小。

图6 两种方案下绿光中心波长和光谱宽度对色域体积的影响Fig.6 Influence of the center wavelength and spectral width of green light on the color gamut volume under the two schemes

通过以上的研究，我们认为，当选用白点色坐标不变的假设时，绿光谱宽对立体色域影响最大，应该最注意绿光谱宽；当选用强度不变的假设时，3种基色对立体色域的影响相当，考虑到红光对白点色坐标影响最小，这时候可以适当牺牲红光的光谱宽度以平衡立体色域和光谱宽度的问题。

4.3 白平衡点色坐标和色域体积变化

使用上述算法，还可以得出显示系统白平衡点色坐标的合理取值范围，这个取值范围应受制于白点和标准点的色差以及白点对立体色域的影响。

白点和标准点的色差为

式中：

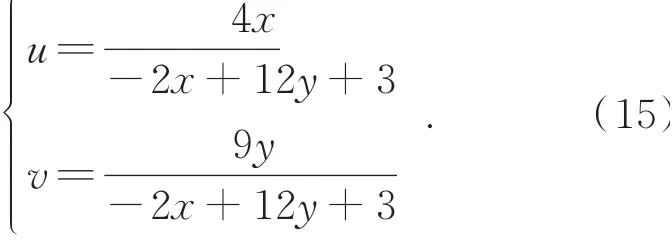
立体色域的影响为

以计算满足三基色波长满足Rec.2020标准，光谱宽度均为1 nm的光源为例，根据式（16）和表1，可以算出

如果我们按照

白点色坐标的取值范围在CIEXYZ色品图中的位置如图7所示。

图7 以D65为参考白光，色域偏移量为3%的白点色坐标取值范围（a）及在CIEXYZ色品图中的位置（b）。Fig.7 Taking D65 as the reference white light，the color coordinate range of the white point with a color gamut offset of 3%（a）and its position in the CIEXYZ chromaticity diagram（b）.

5 结 论

利用全微分公式，在考虑显示系统光源参数影响白平衡点的前提下，研究了中心波长和光谱宽度对立体色域的影响。在固定白平衡点色坐标的前提下，光谱宽度对立体色域的影响同之前一致，为绿光＞红光＞蓝光；在固定基色强度的前提下；3种基色谱宽对立体色域的影响相差不大。其原因在于，对于蓝光，光谱宽度引起的白点坐标变化减少了色域；而对于绿光，光谱宽度引起的白点坐标变化增加了色域。在基色波长选择方面，两种配平因素得到的结论是一致的，波长为520 nm的绿光对立体色域的影响最大，它的光谱宽度增加导致的色域衰减也最大。根据白点坐标和立体色域的关系，我们得出了满足Rec.2020标准，三基色中心波长为630，532，467 nm，光谱宽度为1 nm的光源，每0.01x坐标对立体色域影响为0.80%，而每0.01y坐标对立体色域影响为-2.15%的结果，并据此得出以色域保持3%误差的前提下白平衡点的坐标取值范围。