基于经验小波变换的高墩大跨铁路连续梁桥模态参数识别

王秋萍 唐 剑 霍学晋 秦世强

(武汉理工大学土木工程与建筑学院1) 武汉 430070) (中铁大桥勘测设计院集团有限公司2) 武汉 430074)

0 引 言

高墩大跨连续梁桥是山区铁路建设中常采用的一种桥型[1-2]，其高墩、大跨的结构特点使桥跨结构自振频率低、横向振动效应明显.此外，铁路桥梁运营荷载大，列车运行及制动导致的冲击效应显著.因此，有必要开展试验以了解结构的动力特性.模态参数是结构最基本的动力参数，是进行结构动力分析的基础，准确完备地的识别模态参数有着重要的意义[3-4].

模态参数识别方法可以分为频域法、时域法和时频分析法三类[5].频域法是以傅里叶变换为代表，将时域信号转换到频域进行峰值拾取.傅里叶变换能有效处理线性平稳信号，但在处理非平稳、非线性信号时，由于傅里叶变换是一种时域到频域的全局转换，导致其缺乏时频分辨率.由于快速傅里叶算法中补零和截零的措施往往会导致信号的失真，使识别出的参数不够精确.时域法是从时域信号出发，构建系统状态矩阵然后识别模态参数.时域法避免了时频转换带来的误差，且理论基础完备，因而得到广泛应用.然而，时域法存在系统定阶、虚假模态[6]等问题.时频分析法是以非平稳信号处理工具如经验模态分解(empirical mode decomposition, EMD)[7]、经验小波变换(empirical wavelet transform, EWT)为基础，将非平稳动力信号分解为一系列单频率成分的信号分量，结合随机减量技术和Hilbert变换进行模态参数识别.相比EMD，EWT的理论基础更为完备，在模态混叠、端点效应方面表现更为良好，已经在机械、航空航天、土木工程等领域得到广泛应用.万熹等[8]利用自功率谱替代傅里叶谱进行频谱分割，确定EWT的频带边界，并将其运用于一座斜拉桥模态参数识别，结果表明:采用自功率谱的EWT具有很高的识别精度.向玲等[9]利用EWT解决机械故障诊断问题，结果表明：EWT分解得到的故障频率成分多于EMD，识别精度更高.赵妙颖等[10]将EWT和聚类分析用于变压器振动信号特征提取，结果表明：EWT能准确提取变压器振动信号特征.夏雄等[11]将EWT应用于桥梁模态参数识别，通过数值信号和斜拉桥模型验证了EWT在处理非平稳信号方面的有效性.尽管上述研究验证了EWT在结构模态参数识别方面的有效性，但是仍缺少关于EWT、EMD以及时域随机子空间识别的定量对比和案例分析.

文中结合松头江特大桥动力特性评估和环境振动试验，分别利用EWT、EMD和随机子空间识别三种方法识别桥梁模态参数，对比各种方法识别精度并分析存在的问题.通过工程实例及环境振动试验，基于EWT、EMD结合Hilbert变换进行模态参数识别，进行三种方法识别效果的比对和结果分析.

1 桥梁概况

赣龙铁路松头江特大桥主桥为60 m+2×100 m+60 m连续梁桥，是典型的山区铁路连续梁桥.主桥5#墩墩身高达99 m，桥墩采用圆形空心截面，截面内坡75∶1，外坡40∶1.桥墩最小壁厚0.53 m.主梁截面采用直腹板单箱单室截面，中支点截面梁高7.4 m，边跨直线段及跨中截面梁高3.6 m.主桥立面及测点布置见图1.

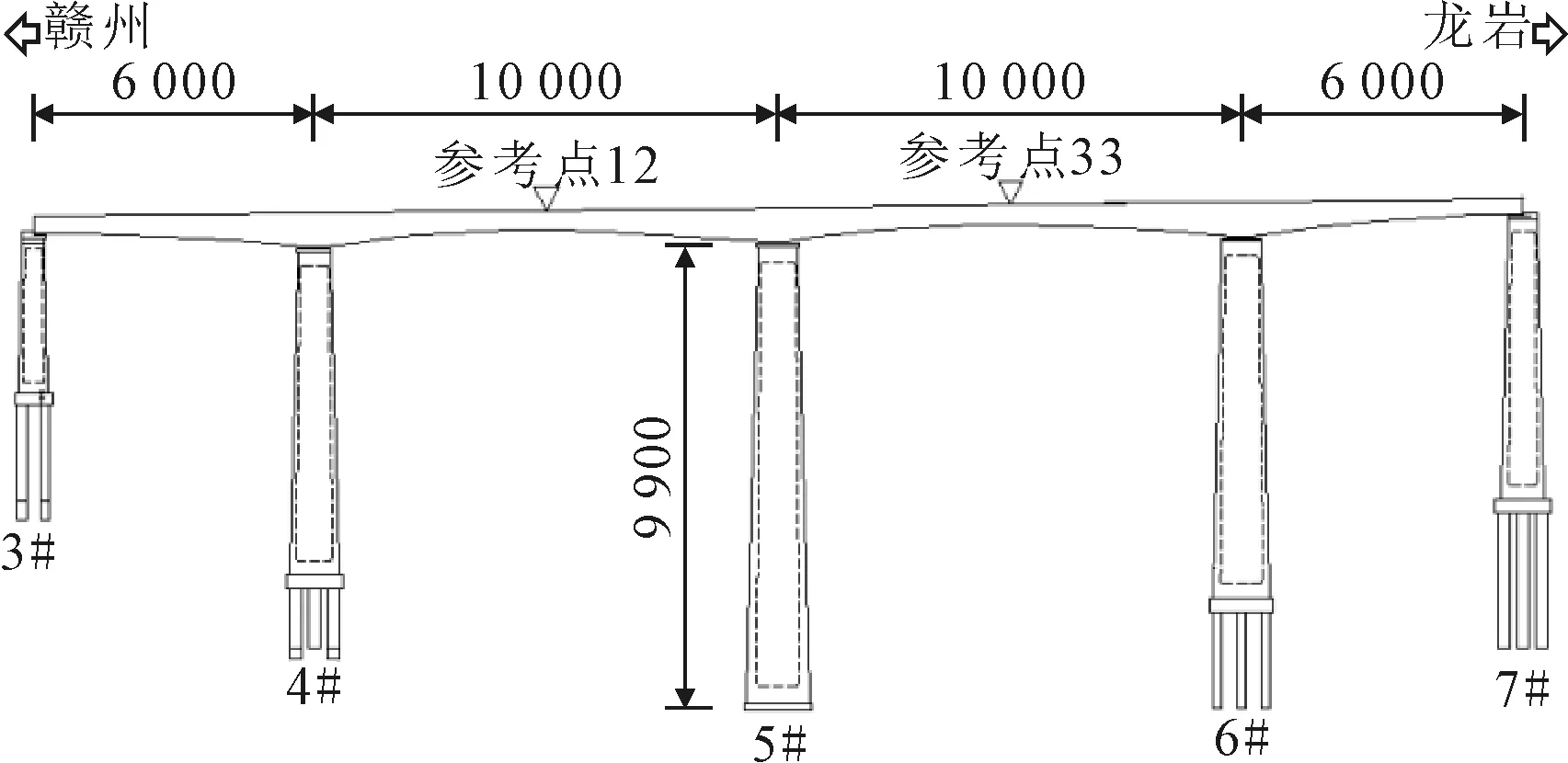
图1 主桥立面及测点布置(单位：cm)

2 环境振动试验

环境振动试验主要测试桥跨结构在风、水流、地脉动等环境荷载作用下的加速度响应，识别桥梁自振频率、阻尼比和振型.环境振动加速度测点布置上，在两个60 m边跨处，测点布置于桥跨八分点处.在两个100 m主跨处，测点布置于桥跨16分点处.测点从赣州侧至龙岩侧按顺序编号，共计布置了49个加速度测点.其中，编号为12和33的测点为参考点，分别位移两个主跨的3L/16、L/2点处(L为主跨跨径).在各个测试组，参考点的加速度传感器连续采样.利用941B型加速度传感器分组测试完成，其中测点12和测点33为参考点.采样频率为80 Hz，每组测试时间为5～8 min.

3 模态参数识别方法

3.1 经验小波变换

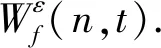
(1)

近似系数通过尺度函数与信号内积产生：

(2)

(3)

经验模态fk(t)定义为

(4)

3.2 EMD方法

EMD通过一种称为“筛”的算法实现，假设x(t)为待处理的原始信号；找出x(t)的所有极大值和极小值，利用三次样条曲线分别拟合极大值点和极小值点，得到原始信号的上下包络线，取上下包络线的平均值为m1(t)，从原始信号中减去m1(t)，得到一个新的数据序列h1(t)=x(t)-m1(t)；判断h1(t)是否满足IMF的两个条件：①整个时程内，极值点和过零点数目相等或至多相差1；②任意一点处，由局部极大值点和极小值点构成的上下包络线的均值为零.

一般情况下，h1(t)不是一个IMF，此时将h1(t)看成x(t)，h11(t)=h1(t)-m11(t)，重复以上过程m次直至h1m(t)满足IMF条件，此时h1m(t)为第一个IMF，称为C1(t)；其次用x(t)减去C1(t)，得到r1(t)=x(t)-C1(t)，并将r1(t)视为新的数据序列重复上述过程，可以得到一系列的Ci(t)和最后一个余量rn(t)，余量rn(t)一般为原始信号的趋势项，为常数或者单值函数.至此，原始信号可以表示为一系列的IMF分量和一个余量之和.

(5)

3.3 Hilbert变换

对每个IMF分量应用Hilbert变换.

(6)

以Ci(t)为实部，yi(t)为虚部构成原始信号的解析信号.

Zi(t)=Ci(t)+jyi(t)=ai(t)ejθi(t)

(7)

式中：幅值ai(t)和相位θi(t)分别为

arctan(yi(t)/Ci(t))

(8)

在此基础上定义瞬时频率为

ωi(t)=dθi(t)/dt

(9)

于是原始信号可以表示成下面的形式.

(10)

与傅里叶变换相比，其幅值和频率为时间的函数，可以说HHT是一种广义的傅里叶变换.将幅度表示在显示在时间-频率平面上，即得到了Hilbert幅值谱，幅值谱精确地描述了幅值在整个频段上随时间和频率分布的规律；对Hilbert幅值谱在时间跨度内积分即得到了Hilbert边际谱，边际谱表征的是含有某个频率的波动在整个时间跨度内出现的可能性.

加速度信号经过EWT、EMD获得单分量信号后，可以结合随机减量技术获取对应的自由振动响应，再按照单自由度系统参数识别方法即可识别结构模态参数.一般情况下，幅值对数及相位不是理想的直线，此时需利用最小二乘法进行线性拟合.

4 试验结果分析

图2为测点4处主桥横向和竖向加速度时程曲线.可以看出，桥跨在环境激励下加速度幅值较小，属于微幅振动响应，横向加速度幅值范围大致在±5×10-3m/s2范围内，竖向加速度响应幅值在±3×10-3m/s2，即横向加速度略大于竖向加速度.对测试得到的加速频谱进行经验小波变换，对加速度信号进行傅里叶变换，结合局部极大值法进行频谱分割，获取单分量信号.图3为横向频谱和竖向频谱分割结果，可以看到，利用局部极大值的包络线，可以很好地对横向频谱和竖向频谱进行分割，各频率成分被较好的区分开，能有效避免频率成分的重叠.

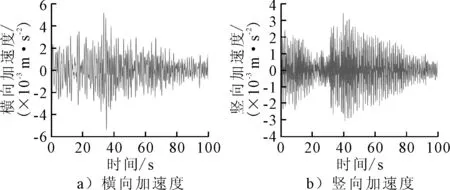
图2 测点4处主桥横向和竖向加速度时程

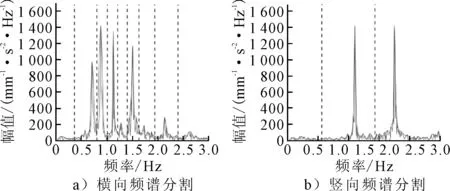
图3 经验小波变换傅里叶谱分割

以测点4的横向加速度响应为例，展示各种方法模态识别的过程.通过EMD得到其各阶IMF(见图4)，每一个IMF均代表结构的模态响应分量，前六阶的IMF分量见图5.利用Hilbert变换可以得到各阶IMF的幅度和相位随时间的变化，即瞬时幅度和瞬时频率，可以表征信号的局部特征.C1是从原始信号中分解出来的最高频率成分，依次往下，频率逐渐降低，而且幅值也在逐渐减小.通常，前几阶IMF占据原始信号的主要成分.

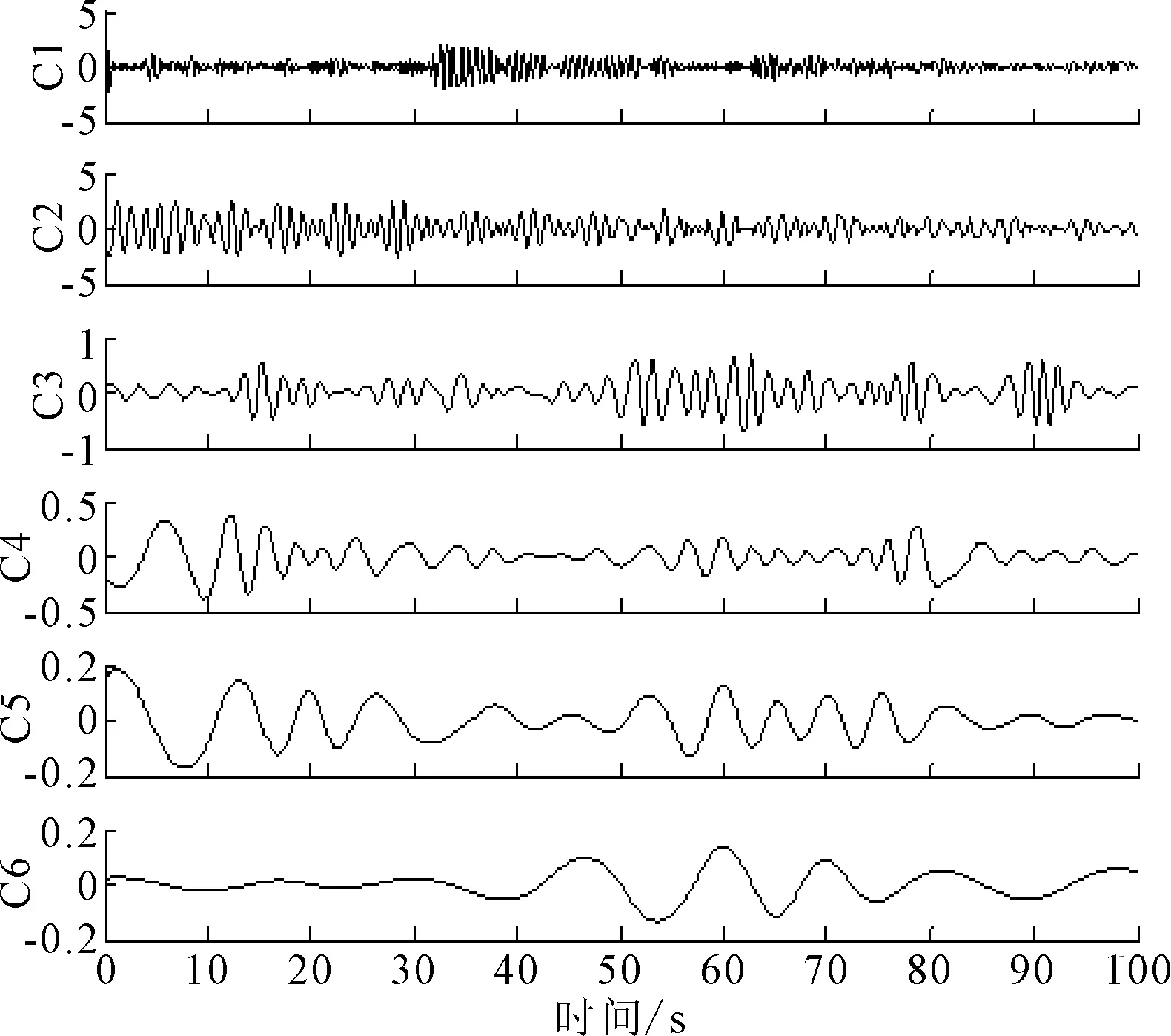
图4 EMD获得的横向加速度前6阶IMF分量

利用EWT和EMD获得信号单分量响应后，结合随机减量技术可以获取单分量响应的自由衰减响应.仍然以测点4横向加速度信号为例，对EWT获得的横向三阶单分量信号进行随机减量，截取的阈值取为原始信号标准差的1.2倍，衰减长度取为20 s，得到图5的自由衰减响应.在得到原始信号的自由衰减曲线后，分别对其幅值曲线和相位曲线进行线性拟合，联立即可求解出频率和阻尼比.图6为对应图5的自由衰减响应的幅值对数拟合、相位拟合图.

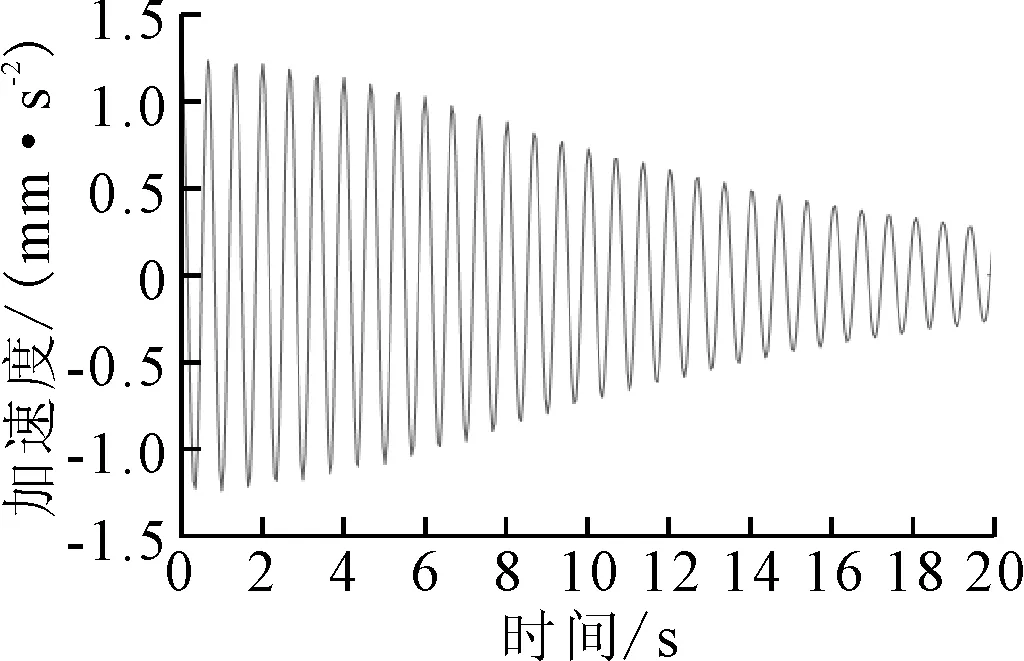
图5 自由衰减响应

图6 幅值对数及相位最小二乘拟合

为了对EWT和EMD方法识别的模态参数进行校核，选择较为成熟的时域随机子空间识别算法作为校核算法.随机子空间识别(SSI)作为一种成熟的时域识别方法，识别过程基于随机状态空间模型，引入了奇异值分解、QR分解、卡尔曼滤波等数学工具，较为适合程序实现，SSI方法的有效性已经过多种工程验证.图7为利用SSI获得频率稳定图，由图7可知：在系统阶次选择为50时，各阶频率形成稳定轴，其余虚假模态则以零星散点形式出现在稳定图中，在1.5 Hz左右，有两条较为明显的稳定轴，需要结合有限元计算进行虚假模态区分.

图7 随机子空间识别得到的稳定图

按照同样的方法，对于其余测点进行模态参数识别，将各测点识别结果求均值并列入表1.表1中SSI、EMD、EWT分别为三种方法的识别结果，EWT-SET表示利用同步提取变换对EWT单分量信号处理后的识别结果.分析表1数据可知：

1) 除竖向二阶外，SSI、EMD和EWT识别结果均小于有限元计算结果，可能的原因包括有限元模型中材料弹性模量偏大、未考虑结构二期恒载的质量效应等原因，表明有限元模型需要按照试验结果进行模型修正.

2) 各种方法识别结果中，SSI与EWT结果更为接近，且与有限元吻合更好；EMD因模态混叠，导致横向三阶频率未识别出来，产生模态遗漏.

3) 各种方法识别的阻尼比数值均较小，符合该类桥型低阻尼特征；但阻尼比识别结果离散性较大，这主要是由于结构阻尼机理尚不明确.

4) 相比随机子空间识别，EWT方法已获得单频率成分信号，不需要结合稳定图进行系统定阶，避免了虚假模态对识别结果的影响.

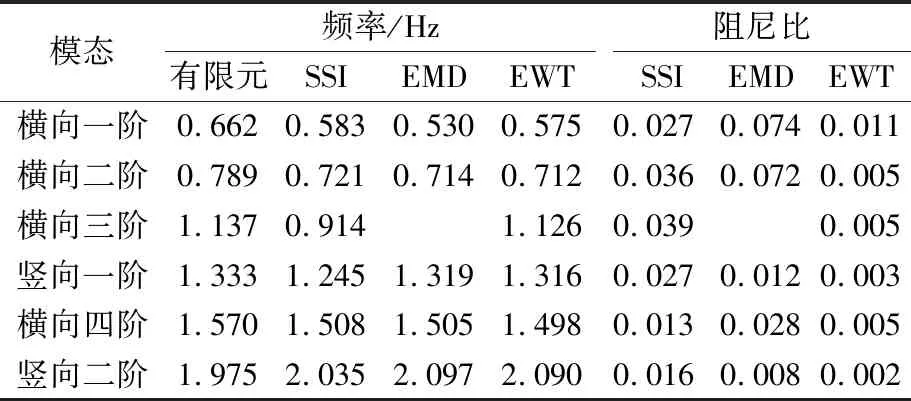
表1 结构模态参数识别结果

5 结 论

1) 该高墩大跨铁路桥梁前10阶自振频率位于0.3～2.5 Hz，自振频率较低；前五阶自振模态中有三阶是横向振动；横向加速度幅值略大于竖向加速度幅值，表明结构横向刚度较低，横向效应明显，符合高墩大跨结构特点.

2) EMD、EWT和SSI三种方法均能识别桥梁结果模态参数参数，且具备一定的精度.除竖向二阶模态外，三种方法识别结果均小于有限元模型计算值，表明有限元模型中刚度模拟偏大、质量模拟偏小，需要结合实测结果对有限元模型进行修正.

3) 相比经验模态分解，经验小波变换能更好地对加速度响应进行频谱分割，避免经验模态分解的模态混叠和模态遗漏，从而更完整的识别结构模态参数；相比随机子空间识别，经验小波变换能更好的适应非平稳信号，避免识别结果受虚假模态影响.