非连续弯曲孔道摩阻预应力损失研究

张开银 王 湃 张 斌

(武汉理工大学船海与能源动力工程 武汉 430063)

0 引 言

对于大跨径预应力混凝土桥梁，主跨跨中下挠过大是其主要病害，致病因素较多且作用机理也相对复杂.近些年学术界认为混凝土的收缩徐变、预应力损失过大和施工质量不达标是造成病害的主要因素[1].因此，预应力钢束的有效预应力是否达到设计标准关乎到桥梁结构的安全运营和正常使用寿命.在现行公路桥涵设计规范中，桥梁结构预应力损失主要原因概括为六项，即管道弯曲摩阻、管道偏差摩阻、张拉锚具变形、混凝土材料弹性压缩、预应力钢筋松弛与混凝土梁体徐变，其中大多数已通过理论分析或试验研究得到了较好的解决[2-3].然而，对总预应力损失占比较大的管道弯曲摩阻预应力损失计算方法一直没有定论，部分学者认为现行桥梁规范中对于管道摩擦系数μ和管道偏差系数k的取值偏小[4].但在实际工程中，仅仅通过选取较大的系数值依旧无法有效的控制预应力损失，往往需要现场实测数据作为参考，费工费时[5].因此，有学者对现行桥规中关于摩擦阻力中接触应力的分布方式提出质疑，文献[6-7]运用CT扫描技术和ANSYS有限元建模得出弯曲孔道的接触应力分布与桥规中假设的均匀分布大相径庭，实际分布规律为弯曲管道中间处应力大，边缘应力小，与弹性接触理论应力分布趋势相同.一系列研究成果表明：现行桥规公式中对弯曲孔道的预应力损失计算方法并不合理，在实际工程应用中也有较大偏差，导致预应力设计的准确度不高，进而引发桥梁的病害问题，需要进行更加深入的研究.

针对上述问题，本文以非连续弯曲孔道为主要研究对象，分析现行桥规公式中对于非连续弯曲孔道的摩阻损失的线性叠加性，发现其与实际验证结果并不相符，以此对桥规公式提出质疑.采用弹性接触理论，对摩擦阻力的接触应力分布状况提出新的假设，弯曲管道中间处应力最大，边缘应力为0，并采用二次曲线进行模拟，推导出修正后的摩阻计算公式.通过模拟计算，验证了修正后公式对非连续弯曲孔道摩阻计算的适用性.在实桥预应力张拉实验中，修正后公式的计算结果也优于现行桥规结果，表明修正后公式的准确性.

1 非连续弯曲孔道摩擦阻力损失

预应力钢筋与管道壁之间摩擦引起的预应力损失可以分为钢筋偏差预应力损失和孔道弯曲预应力损失两部分.钢筋偏差预应力损失是钢筋相对孔道产生的局部偏差导致在张拉时与孔道之间有相对滑动形成的摩擦力造成的，孔道弯曲预应力损失是由于预应力筋穿过弯曲孔道时对孔道内壁产生的径向压力带来的摩擦力造成的.

现行桥梁规范中预应力钢筋与管道壁之间的摩擦预应力损失为

σ=σcon[1-e(μθ+kx)]

式中：σcon为预应力钢筋铀下的张拉控制应力值，MPa；μ为预应力钢筋与管道壁的摩擦系数；θ为从张拉端至计算截面曲线管道部分切线的夹角之和，rad；k为管道每米局部偏差对摩擦的影响系数；x为从张拉端至计算截面的管道长度，可近似地取该段管道在构件纵轴上的投影长度，m.

需要注意的是，现行公式成立需要满足以下假设：①混凝土被视为刚性材料，即在弯曲孔道处预应力筋对孔道内壁的挤压并不会使混凝土产生变形；②只考虑接触物体之间的静力平衡建立弯曲管道与预应力钢束间接触正应力的分布关系，导出接触应力p=T/R，呈现均匀分布.

由式(1)中有效预应力σ(θ,x)与弯曲孔道夹角θ和管道长度x为指数关系可知，对与非连续弯曲孔道的夹角θ1,θ2,…,θn，所产生的预应力损失可以线性叠加.图1的夹角为θ1,θ2,θ3的非连续弯曲孔道和夹角为θ(θ=θ1+θ2+θ3)的连续弯曲孔道为例，A端为钢筋张拉端，若仅考虑孔道弯曲造成的预应力损失，可得：

σA=σcon

σB=σAe-μθ1=σcone-μθ1

σC=σBe-μθ2=σAe-μθ1e-μθ2=σcone-μ(θ1+θ2)

σD=σcone-μ(θ1+θ2+θ3)=σcone-μθ

图1 连续弯曲孔道和非连续弯曲孔道示意图

由式(2)可知，对于同等角度的非连续弯曲孔道和连续弯曲孔道在规范公式下的有效预应力是相等的.但此理论推导的结果却与实际工况中的测试结果并不相符，文献[8]中进行了在多种夹角的工况下，夹角相同的连续弯曲孔道和非连续弯曲孔道的摩阻预应力损失研究，结果表明后者的预应力损失较小.从实验结果看，非连续弯曲孔道预应力损失并不具备式(2)中夹角的可线性叠加性，从而对规范公式的合理性提出质疑.

2 弯曲孔道接触应力分布

2.1 接触应力分布机理分析

由非连续弯曲孔道摩阻预应力损失分析，可以认为仅仅利用了受力物体间的静力平衡关系而没有考虑弯曲孔道挤压所产生的弹性变形，得出预应力筋与孔道内壁的接触应力呈均匀分布并不合理.当把预应力筋和孔道内壁之间视为弹性体接触时，发生变形为弹性变形，接触应力的大小与物体接触面曲率半径和材料弹性模量有关，接触应力为椭球分布，即接触面中心点处压力最大，接触边缘压力为0.

但实际上预应力钢束与混凝土弯曲管道的接触问题属于复杂的三维空间接触，其不完全满足赫兹弹性接触理论中的理想接触条件.并考虑到预应力钢束与弯曲孔道间刚度的差异，其径向应力的分布应介于均匀分布与椭球状分布之间.因此有理由假设预应力钢束与混凝土弯曲管道的接触压力为非均匀分布模式，其接触应力分布示意图见图2.

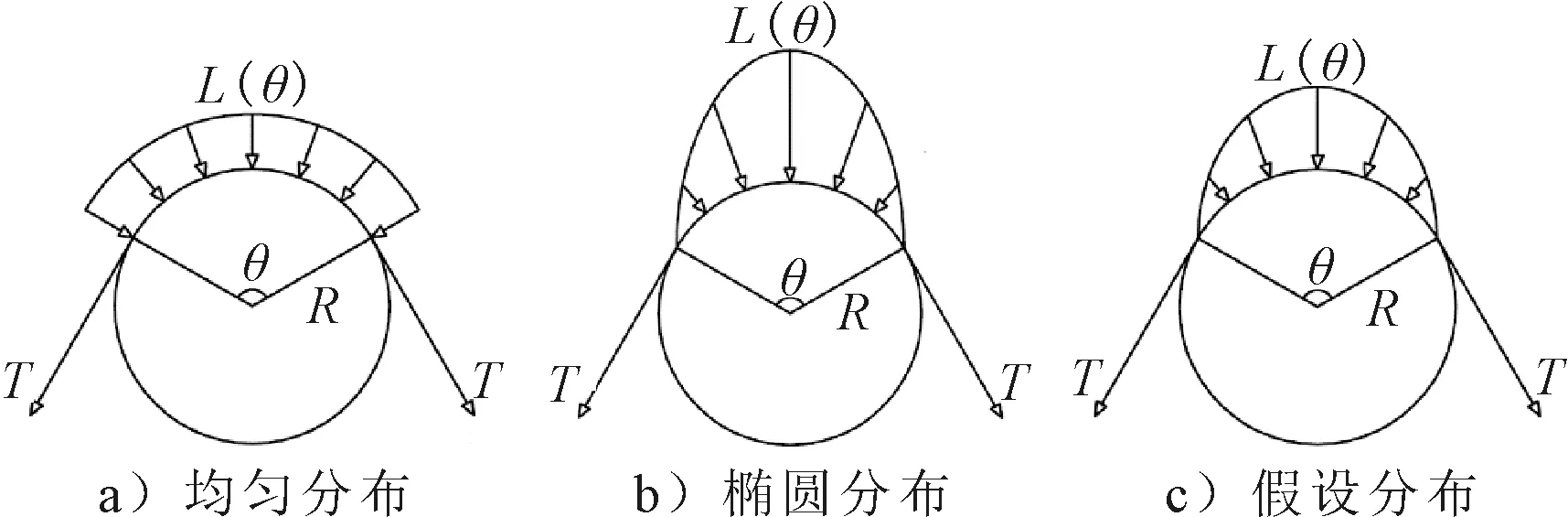
图2 接触应力分布示意图

2.2 接触应力合理重分布

由库仑摩擦定律可知，摩擦阻力与法向接触压力成正比(与接触面无关).张拉过程中由于摩擦力的存在，预应力钢束的有效张拉力将沿程逐渐减小，致使接触正应力及摩擦力也随之减少.考虑到摩擦力对弯曲管道接触正压力的影响不大，对研究问题的力学模型作了适度的简化.

对于一接触角为α、半径为R的弯曲管道，在不考虑摩擦的情况下，假定预应力钢束张拉对弯曲管道的接触正应力函数l(θ)对称分布.弯曲管道接触正应力分布见图3.采用二次曲线模拟接触应力分布，由库仑定律可推导出相应的弯曲孔道摩阻应力计算公式.

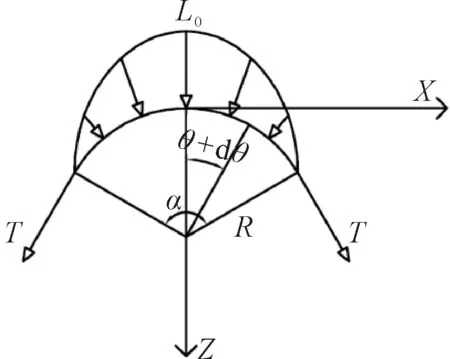
图3 接触应力计算简化模型

设接触正应力的二次曲线分布函数为

l(θ)=aθ2+b

根据应力分布图的对称性可得

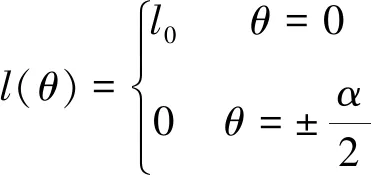
即

由Z方向静力平衡关系

于是解得

则接触应力二次曲线分布下的弯曲孔道摩阻为

2.3 重分布下非连续弯曲孔道计算方法

举例计算非连续弯曲孔道的预应力损失，设张拉端初始张拉力为T1，经过夹角θ1后，末端张拉力变为T2，再经过夹角θ2后，张拉力为T3见图4.

图4 非连续弯曲孔道预应力损失

由式(8)可知：

定义

λ(θ)为摩擦引起的预应力折减系数，则T2=T1λ(θ1)，T3=T2λ(θ2)=T1λ(θ1)λ(θ2).由于λ(θ1+θ2)≠λ(θ1)λ(θ2)，即非连续弯曲管道预应力摩擦损失与连续弯曲管道的预应力摩擦损失并不相等，这与前文所述情况是一致的，证明所假设的重分布模式符合工程实际.所以，计算非连续弯曲管道预应力摩擦损失时，应该分别计算各弯曲段预应力摩擦损失，最后再叠加之.

3 非连续弯曲孔道摩擦阻力损失模拟计算

根据上文结论，对已假设接触应力分布情况的连续弯曲孔道和非连续弯曲孔道的摩阻损失进行模拟计算.设弯曲管道接触正应力二次曲线分布下的连续弯曲孔道摩阻为

Fμ(θ)，非连续弯曲孔道摩阻为Fμ(θ1)+Fμ(θ2)(θ1=θ2=θ/2)，规范采用接触正应力均匀分布的摩阻为F0.假定预应力钢束与弯曲管道壁间的摩擦系数μ=0.18.预应力钢束在张拉力(T=1 kN)下，计算两种不同接触正应力分布下的弯曲管道预应力摩阻损失进行对比分析，其计算结果见表1和图5.

由表1和图5可知：二次曲线接触应力分布下，同等夹角的连续弯曲孔道的摩阻损失大于非连续弯曲孔道的摩阻损失.二次曲线接触应力分布下，连续弯曲孔道和非连续弯曲孔道的摩阻损失都大于规范中均匀接触应力分布下的数值，并且随着夹角的增大，两者的偏差也会增大.

表1 二次曲线分布接触应力下的摩擦阻力

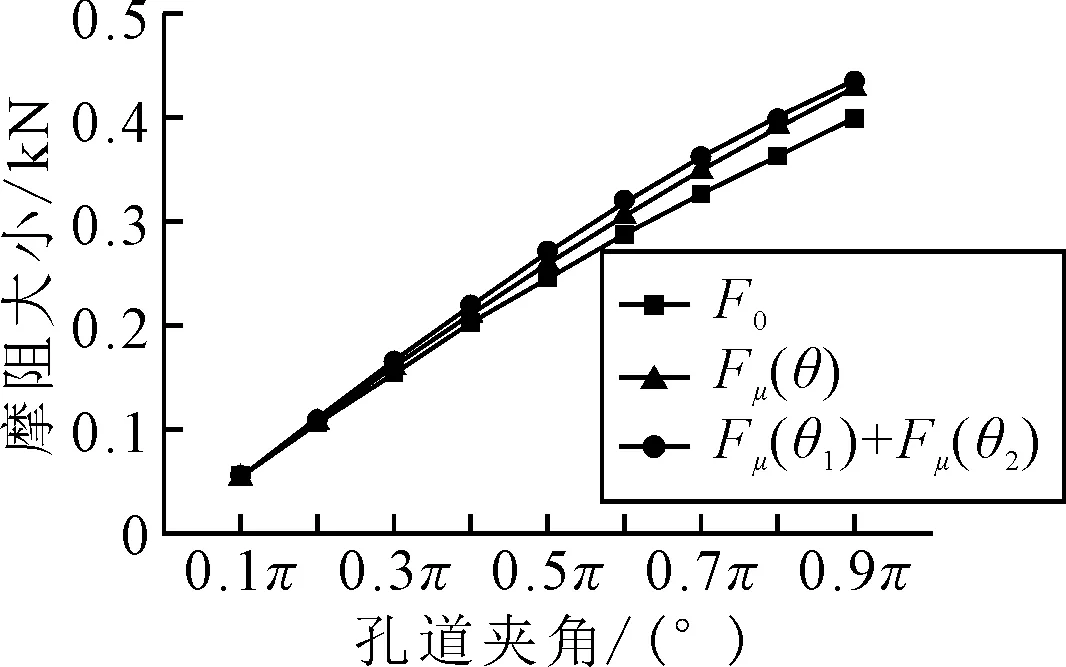
图5 模拟计算结果折线图

按上述理论对现有的桥规公式进行修正，若孔道差引起的摩阻预应力损失仍采用现行设计理论，而孔道弯曲段先分别计算各弯曲段的摩阻预应力损失，再叠加之.则修正后的弯曲孔道摩阻预应力损失表达式为

式中：σcon为张拉端控制应力，MPa；k为单位长度孔道偏差系数；α为等效孔道弯曲夹角，在实际非连续弯曲孔道计算中应该分别计算各弯曲段的摩阻预应力损失，并叠加之；x为张拉端至计算截面的孔道长度，m；μ为预应力筋和孔道壁间的摩擦系数.

4 弯曲孔道摩擦阻力损失试验

按照上述理论，在实际工程中随着预应力混凝土桥梁跨径的不断增大(管道弯曲转角增大、预应力钢束变长、张拉力变大等)，规范公式和实际预应力摩阻损失的差值也将增大，会造成预应力混凝土桥梁在正常使用阶段有效预应力不足，使得混凝土箱梁跨中出现持续下挠、梁体开裂等病害现象，对桥梁结构的运营带来了潜在的安全隐患.

因此，选取主桥结构为三跨预应力混凝土连续箱梁为实验对象，主桥结构采用悬臂浇筑施工法，预应力张拉采用后张法.通过现场检测试验判断预应力钢束的应力损失情况，验证修正后弯曲管道预应力摩阻损失计算公式的合理性与可靠性.

4.1 试验工况

选取主桥腹板预应力钢束其中一根钢绞线为检测对象，并在其对应弯曲管道的部分沿行程黏贴应变片传感元件，布置好信号线并接入应变仪中，见图6.在预应力钢束分级张拉过程中，初张拉15%σcon状态下将静态应变仪调零，然后两端对称、分级、匀速张拉至28%σcon、45%σcon、60%σcon、75%σcon，并依次记录对应工况下各电阻应变片的应变值，见表2.

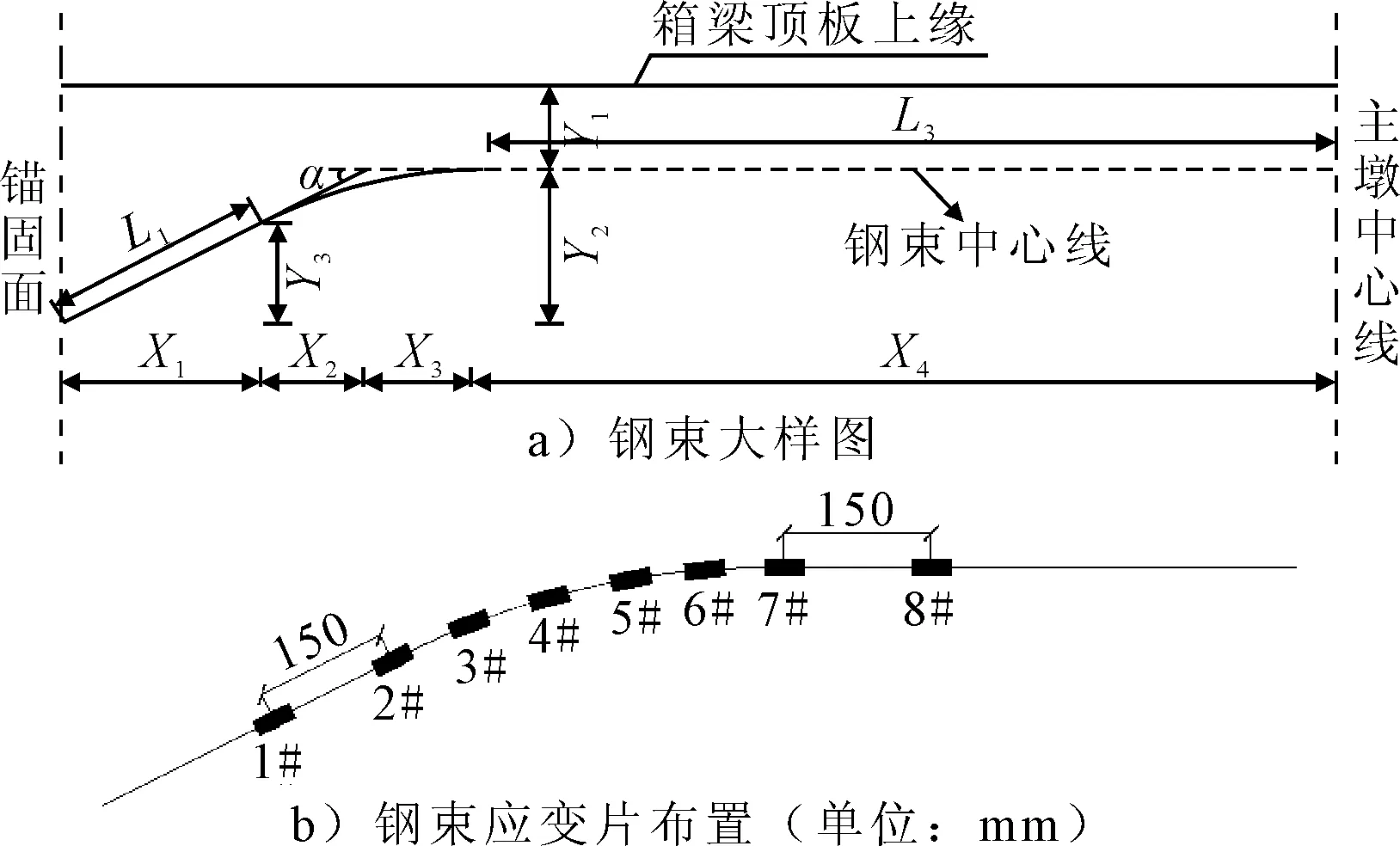
图6 腹板预应力钢束大样图和钢束应变片布置图

表2 腹板预应力钢束几何参数

4.2 试验结果分析

根据设计文件，采用高强度低松弛钢绞线，预埋塑料波纹管，真空压浆工艺.锚下控制应力σcon=1 330 MPa，管道摩阻系数μ=0.18，管道偏差系数k=0.001 51 m.预应力钢绞线参数：公称直径15.2 mm，横截面积140 mm2，弹性模量Es=1.95×105MPa，抗拉强度标准值fpk=1.86×103MPa.预应力钢束在张拉过程中，钢绞线各应变测点实测应变值见图7.

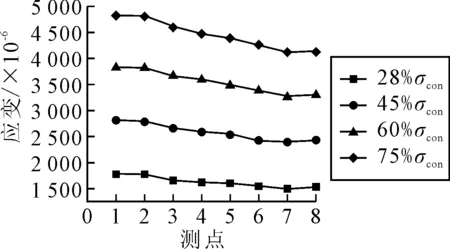
图7 分级张拉测点应变图

由于摩阻作用，预应力钢束距离张拉端越远，有效预应力越小，并注意到位于弯曲管道切点处的2#与7#测点的应变值变化较大，说明弯曲孔道在预应力损失中的影响因子较高.

根据式(1)和式(11)可以计算出分级张拉过程中各阶段的有效预应力(因张拉力较小时应变差距不明显，故只计算后两阶段的计算应变)，再由σ=Eε，可得到接触应力在规范假设和修正分布下各测点的计算应变值，具体结果见表3.

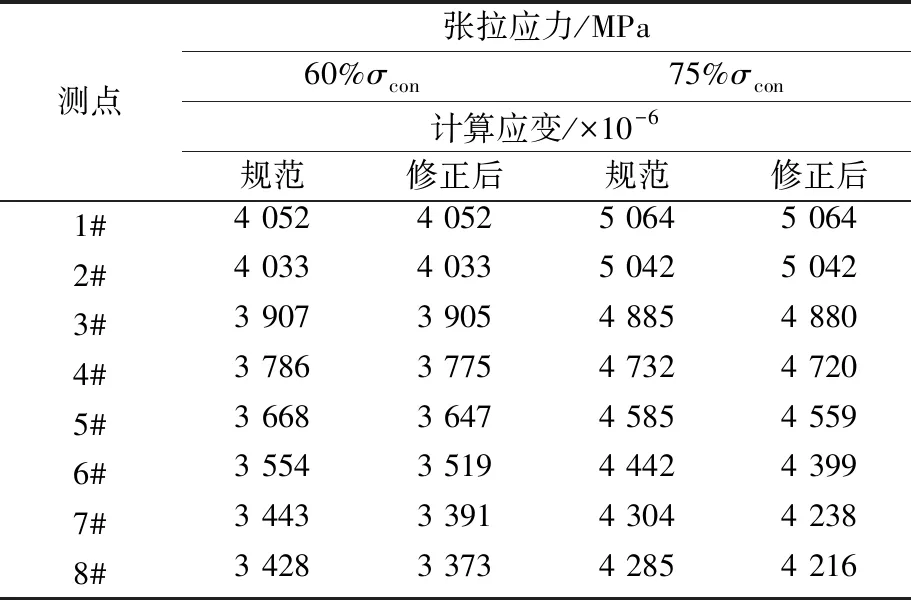
表3 预应力钢束各测点张拉阶段计算应变

图8 计算应变误差分析图

实桥试验结果表明：修正的弯曲管道有效预应力公式计算结果优于桥梁设计规范给定的弯曲管道有效预应力公式计算结果，尤其在弯曲孔道夹角较大时修正公式结果更接近实际测量值；即修正的弯曲管道预应力摩阻损失计算公式相对现有规范更加合理.

5 结 论

1) 现行桥规公式认为非连续弯曲孔道摩阻预应力损失具有角度线性叠加性，这一点与工程实际并不相符.

2) 在计算非连续弯曲孔道摩阻预应力损失时，不能利用角度线性叠加性，应分别计算各弯曲段的摩阻预应力损失，然后再求和.

3) 修正后的弯曲孔道摩阻预应力损失计算公式可应用于实际工程中，为采用后张法施加预应力索的混凝土桥梁设计提供参考依据.