轻量级密码TWINE-128 的量子密码分析*

李艳俊， 易子晗， 汪 振， 刘 健

1. 中国电子科技集团公司第十五研究所 信息产业信息安全测评中心， 北京 100083

2. 北京电子科技学院， 北京 100070

3. 桂林电子科技大学 广西密码学与信息安全重点实验室， 桂林 541004

1 引言

近几年， 量子计算模型下密码算法的安全性成为密码研究人员关注的焦点之一. 1988 年， 3 轮Feistel结构被证明[1]是伪随机置换， 但2010 年3 轮Feistel 结构被发现存在一个固定的周期， 通过使用Simon算法在O(n) 时间复杂度内恢复出周期， 这一结果比经典方法O(nn/2) 的时间复杂度有了很大的提高[2].紧接着在2012 年， 基于Simon 算法Kuwakado 等人对Even-Mansour 结构进行了量子分析， 将恢复密钥的攻击复杂度由传统分析需要的指数时间降低为量子分析需要的多项式时间[3]. 2016 年美密会上，Kaplan 等人[4]对Simon 算法进行了扩充和完善， 并对一系列密码结构工作模式进行了量子攻击， 他们的结果表明在量子计算机下实现的这些结构将不再安全. 在同一年的FSE 上， 他们也提出了量子差分和线性分析[5]. 2017 年， Leander 等人[6]用Simon 算法和Grover 算法组合来攻击FX 结构. 国内的Dong等人[7，8]对广义Feistel 结构构建了密钥恢复攻击， 并结合Simon 算法改进了经典的滑动攻击. 2018 年，Hosoyamada 等人[9]对Feistel 扩展结构进行了量子中间相遇攻击， 结果显示量子计算机能够显著增加中间相遇攻击的能力. 2020 年， Dong 等人[10]结合Simon 算法对滑动攻击进行了改进， 并对Feistel 的一些变体和GOST 进行了密钥恢复攻击. 同年， Luo 等人[11]对三轮MISTY-L 和MISTY-R 进行了区分攻击， 最后论证了在选择明文攻击下， 三轮Lai-Massey 结构能够抵抗Simon 量子算法攻击.

1989 年美密会上， Zheng 等人[12]将一些广义的Feistel 结构总结为Type-I/II/III 型GFS， CAST-256 基于Type-I 型GFS，CLEFIA 和RC6 基于Type-II 型GFS，MARS 基于Type-III 型GFS.其中较为流行版本被称为Type-II 型GFS， 它将消息划分为k个子块(k ＞2)， 并对每两个子块应用一次Feistel变换， 然后执行k个子块的循环移位. 近年来， Type-II 型GFS 因其简单性和高并行性而受到广泛关注.然而， 其缺点是具有较大的k时扩散特性较差. 2010 年， Tomoyasu 和Kazuhiko[13]通过用不同的置换替换循环移位来减少轮数， 可以改善Type-II 型GFS 的扩散特性， 使其达到足够的安全级别. 2019 年，Dong 等人[8]研究了一些广义Feistel 结构的量子区分器， 对于d分支Type-II 型GFS (类似CAST-256的结构)， 引入了具有多项式时间的(2d-1) 轮多项式时间量子区分器. 对于2d分支Type-II 型GFS (类似RC6/CLEFIA 的结构)， 给出了具有多项式时间的(2d+1) 轮量子区分器. 2020 年， Ni 等人[14]在量子选择明文攻击(qCPA)条件下和量子选择密文攻击(qCCA)条件下， 对Type-I 型GFS 进行研究， 给出了改进的多项式时间量子区分器， 并将上述区分攻击应用到CAST-256 分组密码中， 得到了12 轮qCPA多项式时间量子区分器， 以及13 轮qCCA 多项式时间量子区分器， 给出19 轮CAST-256 的量子密钥恢复攻击. 2021 年Li 等人[15]改进了Feisetl 结构密码的量子密码分析方法， 考虑了算法的内部轮函数， 并将该方法应用于Camellia 算法， 提高了量子区分器轮数.

TWINE 算法是2012 年SAC 会议上提出的具有广义Feistel 结构的轻量级分组密码， 旨在保护资源受限的终端设备的数据安全[16]， 分组长度为64 bit， 主密钥长度为80 bit 或128 bit， 分别表示为TWINE-80 版本和TWINE-128 版本. 现有的TWINE 的传统密码分析包括不可能差分故障分析、饱和分析、Biclique 分析、零相关线性分析、中间相遇分析等[17-19]. TWINE 作为广义Feistel 结构的典型密码之一， 目前国内外都没有针对该密码的量子密码分析的相关研究， 本文在改进的Type-II 型GFS 量子区分器的基础上， 将相关区分攻击应用到TWINE-128 上， 设计并实现7 轮区分器， 构造出相关的14 轮密钥恢复攻击路径， 从而降低了攻击代价， 有效地提高了攻击效率. 该方法的提出对于分析轻量级密码算法的安全性具有参考价值.

2 预备知识

2.1 符号说明

2.2 Type-II 型GFS

Type-II 型GFS 中明文输入被分为2d个分支， 用x0j(1≤j ≤2d) 表示， 每个分支为n比特，所以分组长度为2d×n，Fij(0≤j ≤d- 1) 表示第i轮轮函数. 其中每两个块应用Feistel 变换(x，y)→(x，F(x)⊕y)， 然后对子块执行循环位移， 具体如图1 所示. 然而，k值较大的Type-II 型GFS具有明显的缺点， 即它的低扩散性， 需要大约k轮才能将输入差分扩散到所有的输出子块上， 如果输入差分扩散不完全， 会出现一些攻击， 如不可能差分攻击和饱和攻击. 近年来Type-II 型GFS 密码多采用相对较小的k值来平衡规模和效率.

图1 Type-II 型GFS 的一轮加密Figure 1 Encrypt round of Type-II GFS

2.3 改进的Type-II 型GFS

2010 年， Suzaki 和Minematsu[13]找到比循环位移有更好扩散性的块移位方法， 以此提出一种改进的Type-II 型GFS (如图2). 他们用不同的置换替换循环移位， 并证明了这种Type-II 型GFS 具有更快的扩散速度， 使用较少的轮数就可以抵抗不可能差分分析、积分分析等攻击.

图2 改进的Type-II 型GFS 的一轮加密Figure 2 Encrypt round of improved Type-II GFS

2.4 TWINE 算法

TWINE 是一种支持80 位和128 位密钥的64 位轻量级密码， 根据密钥长度的不同， 算法分别记为TWINE-80 以及TWINE-128. TWINE 算法采用16 分支的广义Feistel 结构， 两种密钥长度下， 算法迭代轮数均为36 轮. 轮函数包括3 种操作， 即轮密钥加、4 bit 的S 盒变换以及P 置换， 具体过程如图3 所示， 我们使用以下符号: 第i轮的轮函数被标记为Fi1，Fi2，···，Fi16， 其中Fi1是最左边的一个， 第i轮的轮密钥被标记为RKij(j= 0，1，···，7). 由于具体S 盒置换信息与密钥恢复攻击过程无关， 所以本文不再详述S 盒变换.

图3 TWINE 算法的一轮加密图Figure 3 Encrypt round of TWINE

3 相关工作

3.1 Simon 算法

给定布尔函数f:{0，1}→{0，1}n， 满足f(x)=f(y)⇐⇒x ⊕y ∈{0，s}， 即存在周期s， 经典计算下， 解决上述问题的最优时间复杂度为O(2n/2). Simon 提出一种量子算法， 该算法可提供指数级加速， 并只需要O(n) 量子查询即可找到周期s， 即Simon 算法. 该算法具体步骤如下:

(1) 初始化两个n比特量子寄存器的状态为|0〉n|0〉n;

如果y·s=1， 则|y〉的振幅为0， 因此测量到的y的值都应该满足y·s=0;

(6) 重复前五步(n-1) 次， 可得(n-1) 个线性方程， 解方程即可得周期s.

3.2 Grover 算法

给定布尔函数f:{0，1}→{0，1}n， 存在x满足f(x)=1， 目标是找到符合这个条件的x， Grover 算法可以提供二次加速， 在使用O(n) 个量子比特和O(2n/2) 次查询的情况下解决此类数据库搜索问题， 该算法具体步骤如下:

3.3 Simon 和Grover 结合算法

Leander 和May[6]针对FX 结构， 结合Simon 算法和Grover 算法， 提出了一种密钥恢复攻击方法.FX 结构如图4 所示: Enc(x)=Ek0(x ⊕k1)⊕k2.

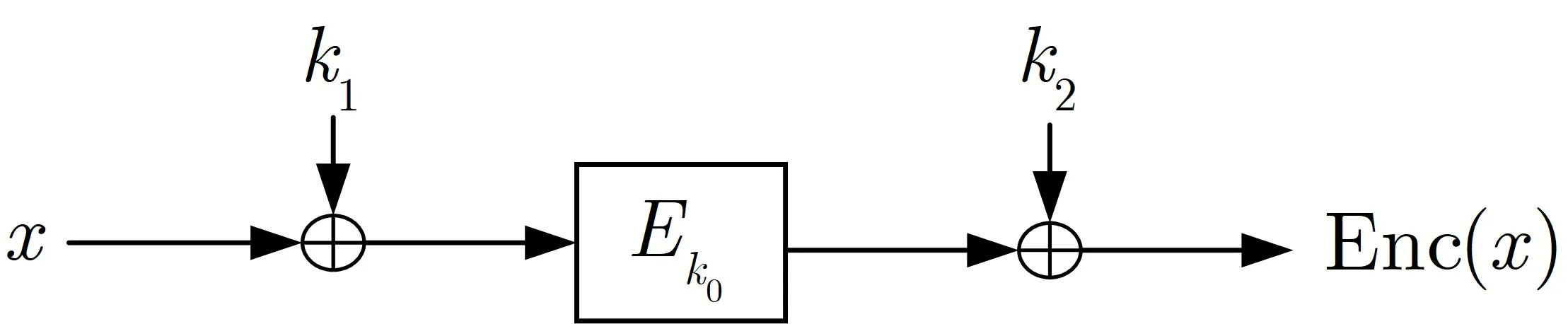
图4 FX 结构Figure 4 FX constructions

构造函数f(k，x) = Enc(x)⊕Ek(x) =Ek0(x ⊕k1)⊕k2⊕Ek(x)， 在猜测正确的密钥k=k0情况下， 对所有x均存在f(k，x) =f(k，x ⊕k1)， 即函数大概率是周期性的; 但对于k/=k0， 函数不是周期性的. 在此基础上， Dong 等人[8]应用Leander 和May 的方法攻击了广义Feistel 结构并给出了5 轮的量子密钥恢复攻击方案， 这种方法相比经典攻击和用Grover 算法穷搜， 时间复杂度都有所降低.

3.4 Feistel 结构的3 轮量子区分器

易证f(b，x)=f(b ⊕1，x ⊕F1(α0)⊕F1(α1))， 即周期s=(1，F1(α0)⊕F1(α1)). 通过Simon 算法可在多项时间内获得周期s.

3.5 Feistel 结构的5 轮量子密钥恢复攻击

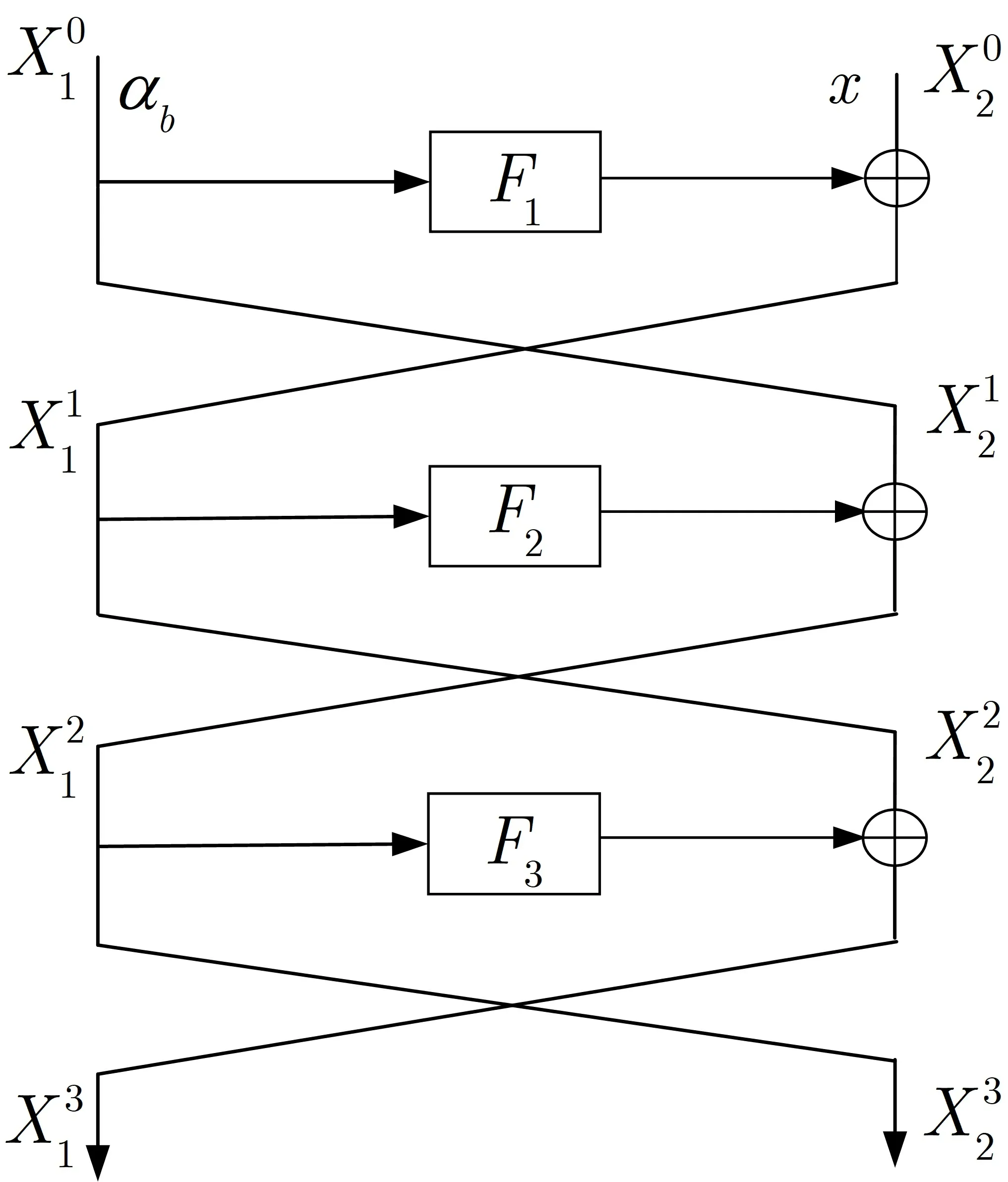
图5 3 轮量子区分器Figure 5 3-round quantum distinguisher

图6 5 轮量子密钥恢复攻击Figure 6 5-round quantum key-recovery attack

3.6 改进的Type-II 型GFS 的7 轮量子区分器

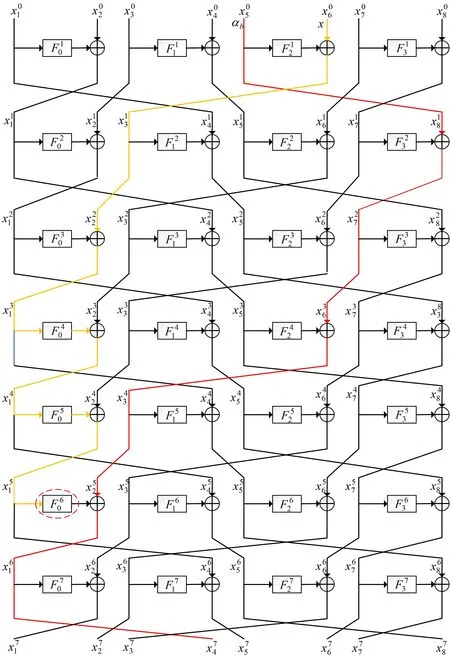
图7 改进的Type-II 型GFS 结构的7 轮量子区分器Figure 7 7-round quantum distinguisher of improved Type-II GFS

4 TWINE-128 的量子密钥恢复攻击

4.1 TWINE-128 的7 轮量子区分器

图8 TWINE-128 的7 轮量子区分器Figure8 7-round quantum distinguisher of TWINE-128

构造周期函数f如下:

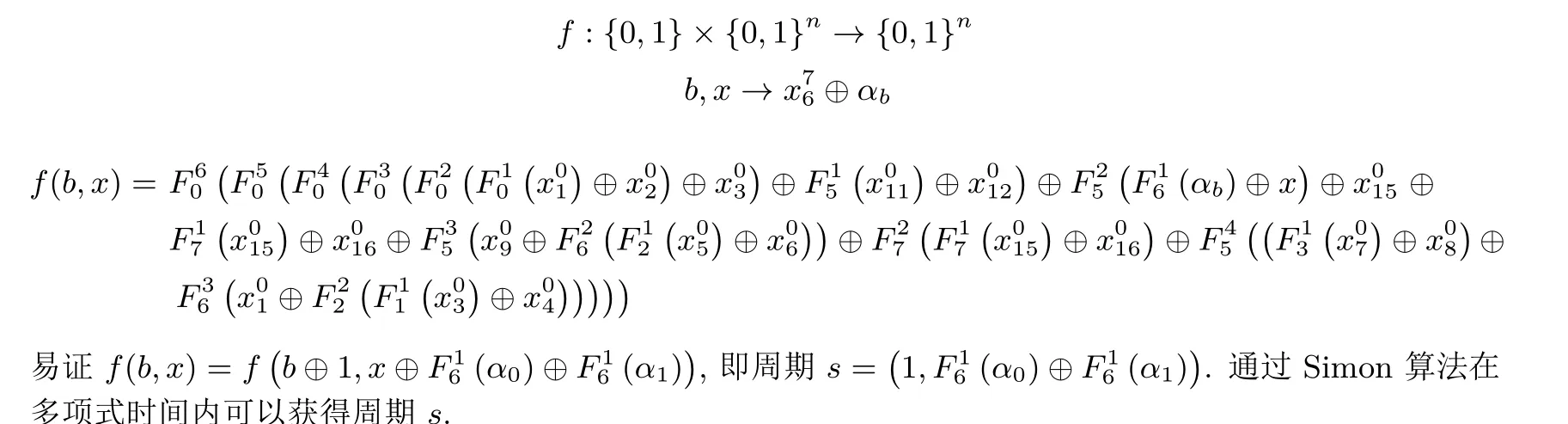
4.2 TWINE-128 的14 轮量子密钥恢复攻击

基于上述提出的7 轮量子区分器对TWINE-128 做量子密钥恢复攻击，采用Simon 和Grover 的结合算法， 在7 轮量子区分器下附加了7 轮来发动攻击. 如图9 所示， 这里有108 比特的密钥需要用到Grover算法进行猜测， 他们被用红色的椭圆线标注了出来， 所以14 轮的密钥恢复攻击需要2(27×4)/2= 254次量子查询. 如果用r表示轮数， 当我们的攻击轮数r ＞14 轮时， 我们需要猜测108+32(r-14) 比特密钥，量子查询次数为254+16(r-14). 根据文献[15]， 密钥恢复攻击所需要的量子比特数可以用以下公式来计算:

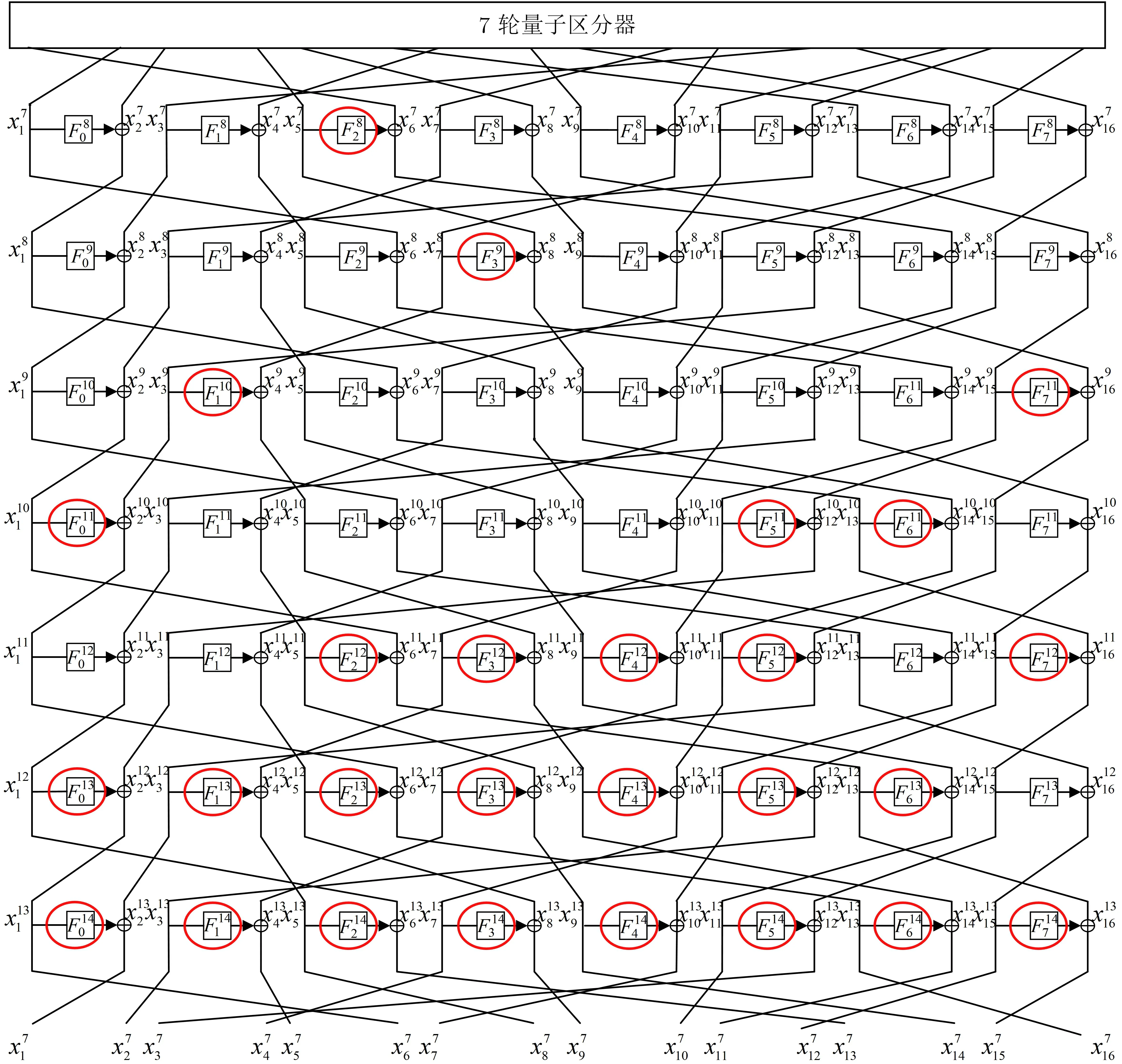
图9 TWINE-128 的14 轮量子密钥恢复攻击Figure 9 14-round quantum key-recovery attack of TWINE-128

其中nk为密钥长度，～n为周期的长度，nin为周期函数输入长度，nout为周期函数输出长度， 本文中猜测密钥的长度为108， 周期长度～n= 1+4 = 5， 周期函数输入长度nin= 1+4 = 5， 周期函数输出长度nout=4， 所以计算可得sum=108+5×15+4×15=243.

5 总结与展望

本文首次在量子计算模型的基础上， 对TWINE-128 进行了密码分析， 通过构造周期函数找到其7 轮量子区分器，然后使用Simon 算法和Grover 算法的结合算法对其进行14 轮量子密钥恢复攻击，该过程所需的量子比特数为243， 时间复杂度为254， 当轮数增加时， 时间复杂度将以每轮216进行递增， 当r ＞14时， 密钥恢复的时间复杂度为254+16(r-14).

下一步工作计划: 我们将在现有研究成果的基础上， 继续探讨可以抵抗量子攻击的分组密码算法的设计方案， 并进一步研究量子密钥恢复攻击技术以减少时间复杂度.