基于改进粒子群的柔性作业车间调度问题优化研究

吴晓雯，郑巧仙

(湖北大学计算机与信息工程学院, 湖北 武汉 430062)

0 引言

作业车间调度问题(job-shop scheduling problem,JSP)是指一个加工系统有m台机器,要求加工n项组装元件,不同的作业包含不同的操作数,假设L为任务集的总操作数.在JSP问题中，每项组装元件的操作时间已经确定，对于元件中的每项操作，其存在相应的先后顺序，每项操作需要按照对应的先后顺序进行加工。对于作业车间调度问题而言，是指将所有组装元件的所有操作进行加工排序，使之满足约束，并且达到目标最优.

柔性作业车间调度问题(flexible job-shop scheduling problem,FJSP)与传统的JSP问题相比，其主要特点是工件的操作可以选择一台或者几台机器进行加工，不存在资源唯一性约束的相关问题.与之相比，由于机器的选择不同，其问题的复杂程度也呈指数级增长.

通过已有的研究发现,研究者们对JSP问题研究透彻,但关于FJSP问题的研究却很少.近年来,因为FJSP问题的复杂性,显示出其更高的实用价值,关于FJSP问题的研究也在日益增多.1993年,Paolo Brandimarte采用分层思想,将禁忌搜索算法同分布思想进行结合,将FJSP问题中的复杂问题分解为几个复杂程度较小的子问题,在对子问题解决的基础上对完整问题进行解决[1].2000年,Maciej Hapke在其论文中,采用模拟退火算法对FJSP问题进行求解[2].

2009年,张国辉等使用改进遗传算法求解FJSP问题,通过考虑各个机器的负荷平衡，建立所有机器总负荷和最大完工时间为优化目标的数学模型,在此问题上提出一种改进遗传算法,提高该种群初始解的质量.并结合问题,设计更加合理的变异算子,提高求解效率[3].2011年,Li等采用关键路径法结合禁忌算法对FJSP进行求解[4].2016年,Li等提出一种新的染色体编码方式,将遗传算法同禁忌搜索算法相结合用于求解FJSP,以此保证种群多样性及良好的全局搜索能力[5].目前，针对FJSP问题,随着“中国制造2025”的提出,智能制造中深度强化学习为构建智能化生产调度系统提供了有效的指导.

1975年,John Holland首次提出遗传算法(genetic algorithm,GA).遗传算法是从其研究问题的解空间的一组解开始进行并行搜索.并且通过计算搜索到的解的好坏，来判定该种群是否需要进行进化.这种搜索方式使得种群以更快速率集中在较好质量个体的区域[6],使该算法的全局搜索能力增强.1995年，Eberhart和Kennedy认为鸟类在觅食过程中，个体之间可以进行信息交流，鸟类的每个个体可以记住自己所处的最好位置，也能找到群体中的最佳位置，这两个最优的位置吸引鸟类朝这两个位置靠近.综合这些特性，他们提出了粒子群算法(particle swarm optimization，PSO)[7].

1985年,Falkenauer首次将遗传算法用于求解传统JSP问题[8],2002年,Kacem首次将遗传算法应用于求解FJSP问题[9].2012年，Lin等混合遗传算法和粒子群算法，并在此基础上提出了混合演化算法[10].2015年,李俊等提出求解柔性作业车间调度的混合粒子群算法，采用基于轮盘赌的编码方式和基于邻域互换的局部搜索方法，并将此编码方式应用于粒子群算法使得柔性作业车间调度问题具有更好的求解性能[11].2017年，刘胜辉等提出了一种分布式粒子群优化算法以求解柔性作业车间调度问题，解决了传统粒子群算法在遇到突发事件时不能实时进行响应并做出合理决策的问题，在该算法中设计了两个多Agent粒子群优化模型，实验表明该算法能够有效解决柔性作业车间调度问题[12].2021年，蔡敏等针对实际工厂中不确定加工时间的柔性作业车间调度问题，提出一种混合粒子群优化算法，采用三角模糊数表示加工时间，以最小化最大模糊完工时间为优化目标进行建模，采用粒子群算法融合模拟退火算法的方法对该模型进行求解，使得改进粒子群算法跳出局部最优，同时也能兼顾搜索速度快等特性，再实例中取得较好的效果[13].

由于将粒子群算法与遗传算法融合用于求解柔性作业车间调度问题的论文较少，大多数都是将粒子群算法同模拟退火算法融合，使粒子群算法的搜索速度兼顾跳出局部最优的能力加强，但在柔性作业车间调度问题中，由于整个作业车间的工序未知，采用遗传算子增加整个粒子群算法的变异能力，在一定程度上也能使得改进后的粒子群算法具有跳出局部最优同时兼顾搜索速度快的能力.针对柔性作业车间调度问题,建立以最小化最大完工时间为目标的数学模型,利用JSP的8*8经典算例和FJSP的Brandimarte算例验证该模型及解的有效性,同时对需要进一步研究的问题和未来发展趋势作出展望.

1 问题描述与模型构建

1.1 柔性作业车间调度问题描述本研究主要针对柔性作业车间调度问题(FJSP)进行求解,柔性作业车间调度问题是在一定的约束条件之下,将各组装元件的操作合理地分配到各机器,合理地安排各操作的加工次序和操作的开始时间,在满足其优化条件的情况下,更好地优化其设定的目标.

将柔性作业车间调度问题(FJSP)描述为：

初始情况下,给定m台机器,以及n项组装元件.按照元件的工艺路线,每项组装原件由一种或者多种有顺序约束的操作组成.每种操作可以在多台机器上进行加工.操作进行加工的过程中,需要满足以下约束条件：

1)同一时刻,每种操作只能在一台机器进行加工,若操作开始加工,直至加工完成，此项操作不能被中断；

2)同一时刻,每台机器最多只能选择一种操作进行加工；

3)同一组装元件间的操作之间存在先后约束关系，不同组装元件的操作之间不存在顺序约束；

4)不同的组装原件之间具有相同的加工优先等级.

1.2 柔性作业车间调度问题模型构建基于以上假设,构建柔性作业车间问题的数学模型,表1给出模型的参数含义：

表1 模型参数含义

根据问题描述,建立以下优化目标：

(1)

dijk={0,1},i,j∈Oij

(2)

(3)

(4)

其中：式(1)表示该问题的目标为最小化最大完工时间；式(2)保证每个组装元件的每一项操作同一时间只能分配至一台机器；式(3)是其中的顺序约束,即在对同一组装元件的不同操作进行加工时,某项操作j如果需要在另一项操作j1之前完成,则该项操作应该优先被分配至机器；式(4)表示所有机器的完工时间之和不超过目标函数.

2 粒子群算法(PSO算法)

(5)

(6)

一般而言，PSO算法是一种基于自身经验和社会经验不断学习的算法，它具有较强的通用性，且群体在进行搜索时具有记忆能力，粒子间联系紧密，学习能力较强，也可以根据问题的规模自动调整学习速度，搜索速度较快，原理较为简单，但其局部搜索能力较差，搜索的精度有待提高，而且容易因为参数的设置问题而陷入局部最优解，所以针对粒子群算法的特点，将遗传算法中的遗传算子引入粒子群算法中，在粒子陷入局部最优解的过程中对粒子进行交叉变异，从而可以使得PSO算法跳出局部最优解.

3 改进粒子群算法(IPSO算法)

本研究主要采用改进粒子群算法对FJSP问题进行求解,针对粒子群算法中的惯性因子进行自适应调整，在算法运行过程中，将遗传算法中的遗传算子引入粒子群算法中，提高算法的深度寻优能力.

3.1 惯性因子调整策略首先针对惯性因子采取自适应调整策略，基本的粒子群算法的惯性因子是固定的，在PSO算法中，一个较大的惯性因子有利于全局搜索；反之，适合局部搜索，所以固定的惯性因子并不适合复杂的FJSP问题.此时，需要将惯性因子调整为自适应改变自身大小，在需要全局搜索时自动增加其大小.以式(7)对惯性因子进行更新：

(7)

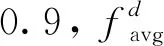
3.2 工序交叉与工序变异在PSO算法中，由于粒子只能通过速度的大小和当前的位置来寻找最优位置，由于参数设置的问题，极易陷入局部最优位置，如何跳出局部最优位置，找到全局位置成为改进算法的关键之处，本研究将遗传算法的遗传算子引入粒子群算法中，对工序采用编码、交叉、编译等方式，进一步提高粒子的搜索性能.

3.2.1 工序编码 对于已经过位置和速度更新的粒子，寻找粒子适应度值位于前30%的粒子，对该粒子所处位置进行染色体编码，染色体的长度与总操作数相等.每一个基因用组装元件号直接编码,元件号出现的顺序表示该元件操作间的先后加工顺序.此时,对染色体从左到右进行编译,对于第q次出现的元件号,表示该元件i的第q项操作,并且元件号的出现次数等于该元件的操作总数.对工序编码之后，根据柔性作业车间调度问题的特点，需要进行机器选择，选择当前工序完工时间最小的机器进行加工.

3.2.2 工序交叉 对于已经进行编码的工序，对其染色体进行交叉，以父代新的组合方式产生新的粒子，并计算新的适应度，若新的粒子的适应度的值优于原先粒子的适应度，则将其进行替换.

3.2.3 工序变异 若此时产生新的粒子的适应度与原先的相比无变化或者大于原先粒子的适应度，则将染色体进行变异，设定变异概率P_variation，且P_variation≤0.05，对交叉粒子集中每个粒子的每一位，产生一个随机数r⊂[0,1]，若r≤P_variation，则将该位取反，否则该位不变.对变异后新的粒子，进行适应度计算，若新粒子适应度优于原先粒子的适应度，则将其进行替换.

该算法求解FJSP问题的流程伪代码如下所示.

1) 初始化：设置参数，设置变量；

2) 生成种群，设置最大迭代次数；

3) 计算每个粒子的初始适应度值，并将其初始适应度值作为每个粒子的局部最优值，保存其局部最优值，从局部最优值中选取最好的值，并将该值作为初始的全局最优值；

4)While 未到迭代次数 do；

5)根据式(5)～(7)对粒子位置和速度进行更新；

6)计算当前种群粒子的适应度，更新粒子最优位置；

7)对FJSP问题中的工序进行编码；

8)针对该编码方式对工序进行交叉，计算交叉后产生新粒子的适应度；

9)若新的粒子适应度值>原粒子的适应度值；

10)粒子替换；

11)若新的粒子适应度值≤原粒子的适应度值；

12)工序变异；

13)计算变异后产生新粒子的适应度，将选出的最好适应度值的粒子所处的位置设定成为全局最优位置；

14)生成新的粒子群；

15)End while；

16)根据最终结果更新最好解.

4 实验结果与分析

为了验证该问题具有可行解及算法的性能,算法在Windows10下使用python进行求解,在11th Gen lntel(R) Core(TM) i5-1135G7@2.40 GHz CPU,16 GB内存PC上运行.对于车间作业调度问题的8*8算例和柔性作业车间调度问题的Brandimarte算例进行测试.

初始情况下,设定种群数量pop_size=30,交叉概率P_cross=0.8,变异概率P_variation=0.05,最大迭代次数max_iterations=30,8*8算例求解的最大完工时间Cmax=15,该算例的甘特(Gatt)图和收敛图如图1和2所示.

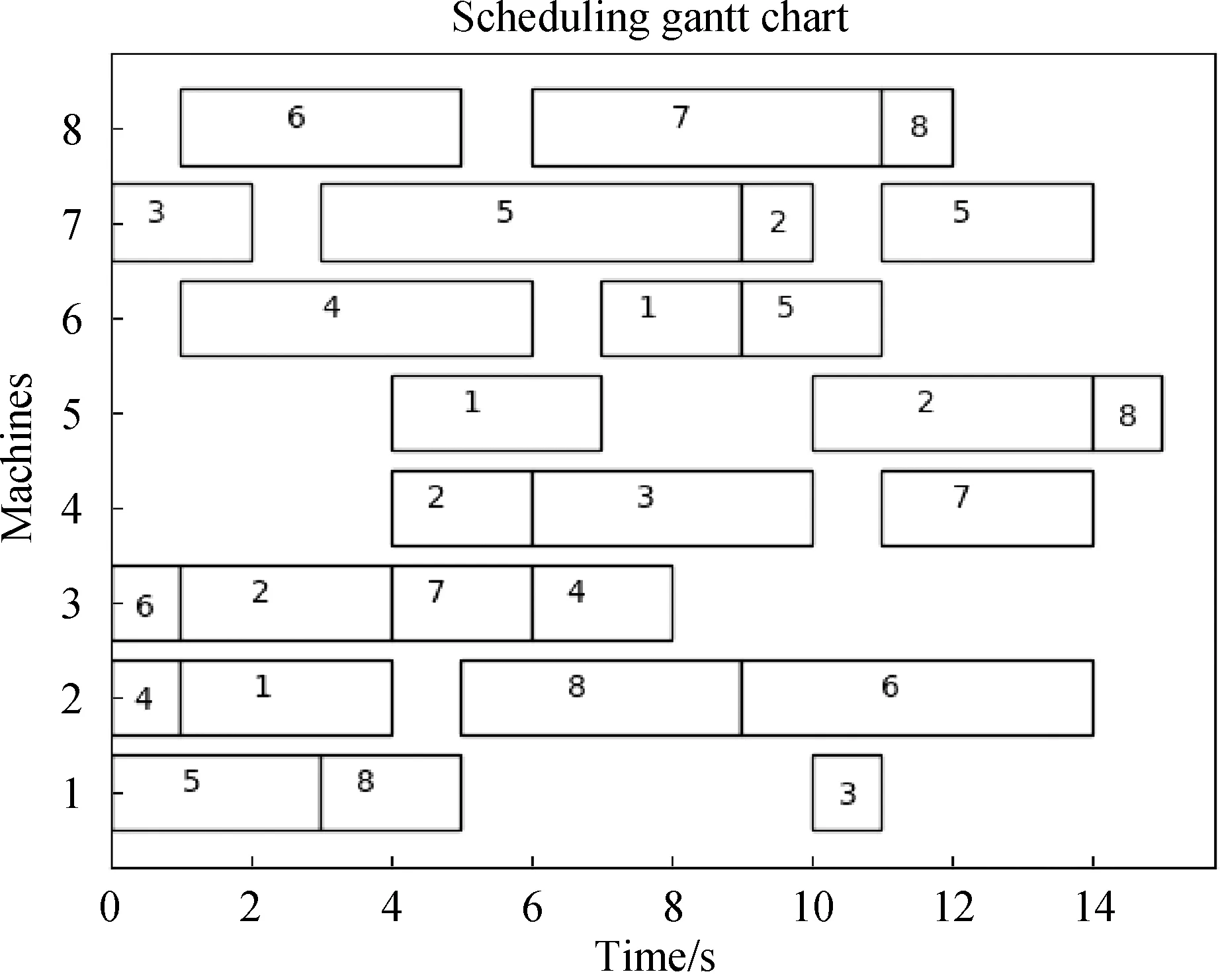
图1 8*8算例Gatt图

种群数量和迭代次数改变后,车间作业调度问题的8*8算例的结果如表2所示.

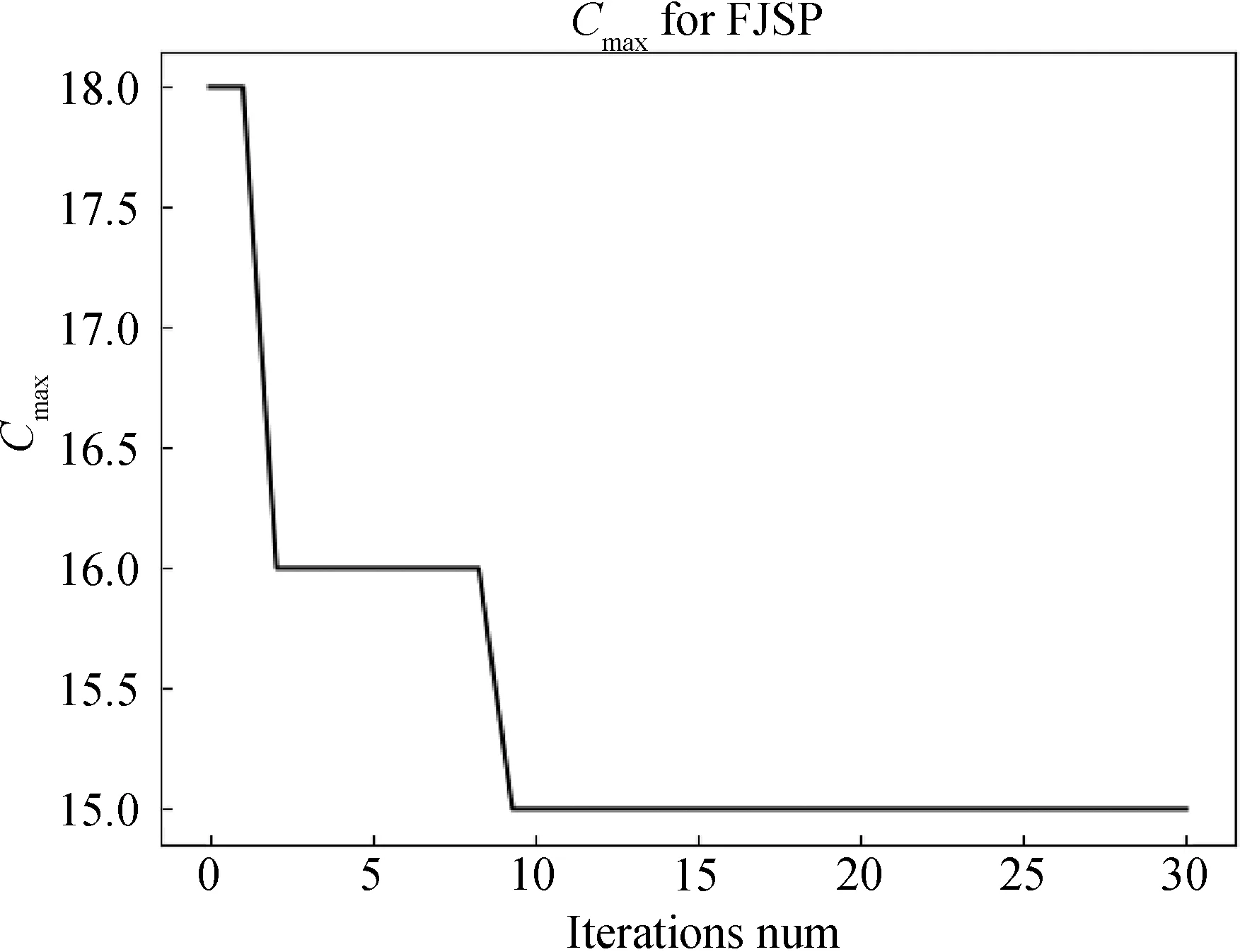
图2 8*8算例收敛情况

表2 种群数量和迭代次数改变后的8*8算例最大完成时间

由表2结果可以看出种群数量和迭代次数对最小化最大完成时间都具有一定的影响，其中种群数量为300,迭代次数为50次得到的解最好,最小化最大完工时间Cmax=14.并且初始情况下,最小化最大完工时间Cmax=17,与其他情况相比,此情况下的解较好.

为了更好地检测算法的有效性,对Brandimarte算例进行测试,Brandimarte算例中含组装元件10项,机器数6台，总操作数58项.在给定初始条件下,Brandimarte算例求解的最大完工时间Cmax=29,该算例的甘特图和收敛情况如图3和4所示.

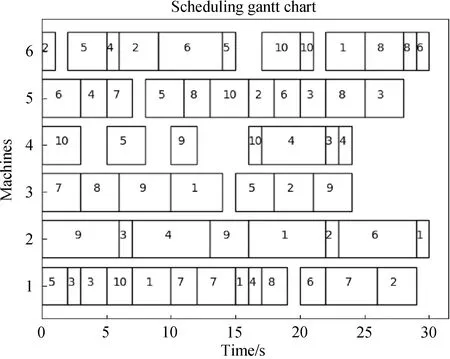
图3 Brandimarte算例Gatt图

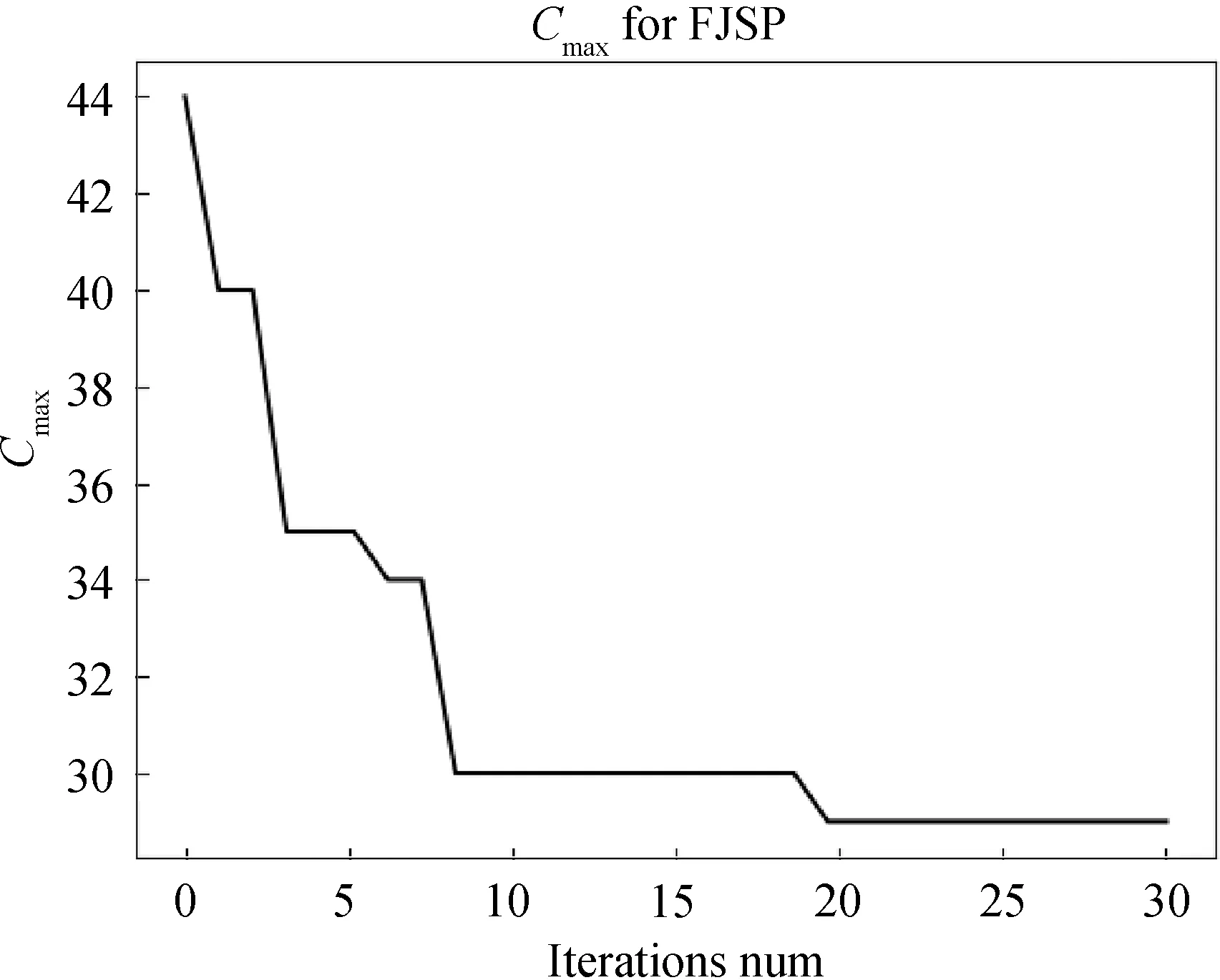
图4 Brandimarte算例收敛情况

该算例的求解结果如表3所示：

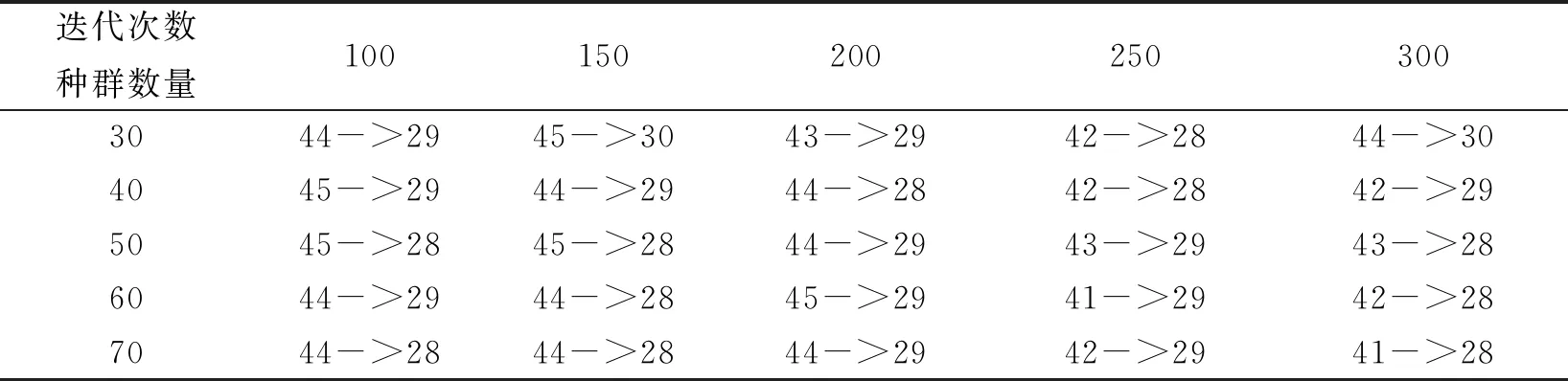
表3 种群数量和迭代次数改变后Brandimarte算例最大完成时间

由上表结果可以看出种群数量和迭代次数对最小化最大完成时间都具有一定的影响，其中种群数量为300,迭代次数为50次得到的解最好,最小化最大完工时间Cmax=28.并且初始情况下,最小化最大完工时间Cmax=41,与其他情况相比,此情况下的解较好.

5 结论

本文中采用IPSO对FJSP进行求解，在粒子群算法的基础上，将遗传算法中的遗传算子加入粒子群算法中，根据FJSP问题的特点，提出针对机器排序和操作选择的编码过程，在后续的染色体交叉和变异过程中，同样考虑机器排序和操作选择的过程.这样进一步提升了种群的多样性，避免粒子群算法陷入局部最优解，同时使得求解速度加快，求出更好的最优解.下一步将探讨使用改进粒子群算法求解在人为因素和中途中断等条件下的柔性作业车间调度问题.