MEMS微镜动力学模型修正技术研究

沈婧怡，丁晓红，张 横

(上海理工大学机械工程学院，上海20093)

0 引言

目前，结构分析方法主要分为两种，一种是通过有限元分析对结构动力学进行仿真分析，另一种是通过试验对其动力学特性进行分析。在MEMS（Micro Electromechanical System）微镜结构中，由于MEMS 微镜尺寸小、结构复杂、极易受外部载荷损坏，实际试验存在以下问题：①试验成本高；②单个结构损坏后再次试验周期长；③试验结果受实物制造工艺影响大。利用有限元模型进行仿真可以降低时间及经济成本，因此提高有限元模型计算精度、降低有限元仿真与试验间的结果误差变得尤为重要。

模型修正技术多用于航空航天、机械、古文物修复等领域，最早出现的模型修正方法是矩阵型修正方法，该方法以系统总矩阵或子结构矩阵为修正对象，代入正交性条件或者运动方程求出偏差，该方法会改变原结构矩阵并出现物理意义不明确的问题，因而逐渐被元素型模型修正方法所取代。元素型模型修正方法的修正对象是矩阵元素结构的设计参数。本文针对MEMS 微镜的动力学有限元与试验分析之间存在较大差异的问题，利用元素型模型修正的方法，通过以误差最小作为优化目标，对比试验获得的模态分析结果，对结构进行有限元模型修正，获得满足工程需要的高精度有限元模型。修正后的有限元模型可以作为后期相关分析的基础模型，如微镜谐响应分析、冲击振动分析、结构减振设计、结构轻量化设计等研究。

1 有限元模型的修正

固有频率是动力学分析中基础参数，对于关注低阶模态的情况，测量固有频率比模态向量更简单。在有限元模型修正过程中，包括以下五个部分：预试验分析、相关性分析、参数和响应选择、灵敏度分析、参数修正。

通过预试验分析，优化激励和响应传感器位置的优化布置，从而提高试验精度；通过相关性分析评估数值模型特征和实际结构之间的一致程度。试验测量频率F与有限元计算频率f之间的相关程度通常表示为：

本文主要以某企业MEMS 微镜为研究对象，首先通过试验获取微镜的前4 阶固有频率及振型，然后再建立有限元模型。由于微镜表面镀层材料参数、厚度及加工工艺都会对微镜本身的动力学特性产生影响，因此用调节微镜厚度的方式模拟镀层。通过元素型模型修正的方法，以试验测量的频率与有限元分析得到的频率差值最小为目标函数，将微镜结构各部分厚度作为设计变量，对比相同频率下振型是否一致，如果不一致则继续修改，如果一致，则提取各部分厚度的具体数值，通过细微调整尺寸参数来建立精确的有限元模型。

2 微镜的试验模态分析

试验模态分析通常由激励系统、测量系统和数据处理系统组成，通过对结构施加外部激励，当所施加的外部激励的频率与结构本身的某一固有频率相同时，结构出现共振，由此得出结构的固有频率。本文研究对象MEMS 微镜本身质量较轻，传统测振技术所使用的加速度传感器其测量误差无法忽略，因此采用无附加质量影响的多普勒激光测振技术对MEMS微镜进行试验模态分析。如图1 所示为多普勒激光测振的原理。

图1 多普勒激光测振仪原理示意图

试验时，将微镜固定在支架上，激光测振仪连接数据采集仪放置在微镜前端，调节相对位置，使用激光测振仪信号达到最佳后，将微镜通电，光学头采集微镜的速度信号，采集仪进行数据采集，由软件处理得到前4阶固有频率，如表1为其数值及振型描述。

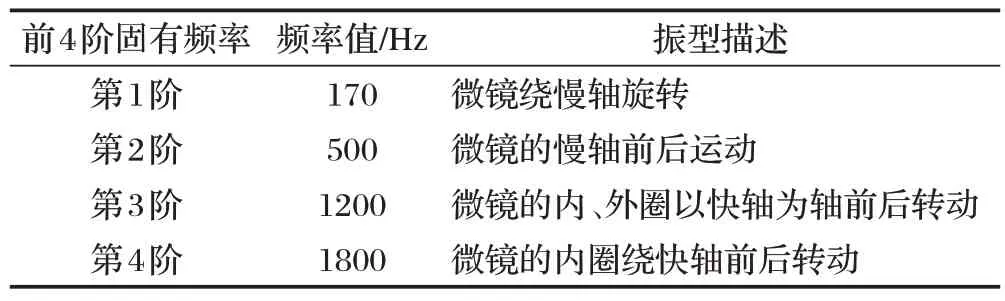
表1 微镜模态分析的前4阶频率及振型描述

3 有限元模型的建立及模型修正

如图2 所示为由微镜-封装组成的MEMS 微镜结构，微镜表面包括Zn-Al 镀层、线圈等，有限元模型中通常忽略这些结构，但是实际上微镜镀层会对结构的刚度和质量分布产生一定影响，从而影响结构的动力学特性，因此这种忽略镀层的有限元模型建立方式会导致分析结果与试验结果不符合，需要对微镜的有限元模型进行修正。本文通过将微镜与镀层视作一体，小范围调节整体厚度，模拟微镜镀层厚度的改变，从而实现对镀层厚度的修正。为了减少计算规模，对微镜结构的有限元模型进行简化，简化一些对有限元模型分析影响较小的几何特征，从而减少网格数量，提高运算效率。

图2 某企业MEMS微镜结构

如图3所示为简化后的微镜模型，其有限元模型、约束及网格划分如图4所示。微镜分为外框、内框、镜片、快轴及慢轴五个结构，镜片通过慢轴与内框连接，内框通过快轴与外框连接，外框两侧设置全约束，外框长度30mm，宽度20mm，内部镜片部分直径为6mm，快轴宽度为0.5mm，慢轴宽度为1mm，由于微镜厚度远小于其长度及宽度，且考虑到计算成本，通过将原有的三维模型抽取中面进行模型建立并划分四边形网格，结构间采用网格共节点的方向进行连接，网格单元尺寸0.5mm，单元数2084，节点数2329。初始计算材料弹性模量130GPa，泊松比为0.28。

图3 MEMS微镜结构图

图4 优化后各阶固有频率下的振型对比

图4 MEMS微镜结构有限元模型

目前，结构动力学模型修正可以分为矩阵型修正方法和元素型修正方法。元素型方法源于Fox 等人的研究工作，该方法以有限元模型的参数，如材料参数、形状参数及尺寸参数为修正对象，该方法可以视为单目标函数优化问题，目标函数为数值模型和实际结构之间的差值最小，通过对合适的参数进行修正以达到目标函数最小。在本文研究中通过设计参数型修正方法，以材料属性参数、结构尺寸参数为设计变量，前两阶模态差值最小为目标函数，从而，得到修正后的数学模型：

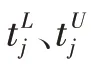
根据上述建立的数学模型，通过迭代优化过程，获得最终的设计空间参数向量，实现模型修正。本文设计空间的设置以及优化后的厚度值如表2所示。

表2 设计变量参数表/mm

4 修正后微镜结构的模态对比

按修正后微镜厚度参数对微镜结构进行模态分析，可以得到其前6 阶固有频率及振型。表3 所示为微镜结构前6 阶固有频率，如图5 所示为试验以及优化后微镜的振型图。经分析可以看出，该微镜前4 阶固有频率与试验分析得到的频率与振型一致，第1 阶固有频率的误差为2.23%，第2 阶固有频率的误差为5.6%，第3阶固有频率的误差为6.4%，第4阶固有频率的误差为8.6%，前4 阶固有频率误差基本保持在10%的范围内。

表3 微镜模态分析的前6阶频率及振型描述

5 结束语

本文针对MEMS 微镜有限元模型动力学特性分析与试验分析结果相差较大的问题，运用了元素型模型修正方法对其中影响较大的微镜厚度进行了参数优化，修正微镜的有限元模型。经过修正后的模态分析结果与试验结果，误差控制在5%以内。通过这种参数优化技术，实现了对微镜模型的动力学修正，为微镜模型修正提供了一种较为简单实用的方法。