基于社会粒子群算法的蒸发器模型参数辨识*
张 迎,赵星凯
(山东建筑大学信息与电气工程学院,山东 济南 250000)
0 引言
众所周知,蒸发器在空调末端制冷系统中扮演着非常重要的角色,所以蒸发器模型的建立就显得尤为重要。由于蒸发器内的制冷剂通过相变进行换热,两相区与过热区的换热面积随工况条件实时的变化,而两段区域的换热系数巨大的差异会引起蒸发器换热效率的巨大变化。
通常通过理论建模和数据建模对制冷系统的蒸发器进行建模。Zhang和Zhang建立了一个基于移动边界方法的通用模型来描述蒸汽压缩制冷系统中干式膨胀蒸发器的瞬态行为。两相区和过热区之间的界面温度是通过新的加权平均值来评估的,本模型可以很好地预测蒸发器在较大干扰下的瞬态行为,并在过热区出现时保持了稳健性。Xudong Ding等从基本的物理原理开始,仅捕捉几个关键的操作特性参数来预测系统性能,建立了蒸发器混合模型,该方法利用了物理和经验建模方法的优势,可以准确地预测宽范围内的性能该模型用取自测试系统的实验数据进行了验证,测试结果表明,所提出的模型可以准确地预测实时运行的蒸发器的性能,最大误差为±8%。ChenGuang Ning 等基于体积效率的概念和多变量压缩过程的假设,对质量流量进行分析,提出了一种混合稳态压缩机模型,大多数蒸发器建模都是采用离线建模。
如今科学技术快速发展,那些普通的辨识方法越来越不能满足现实需求,很多新型的智能算法涌现。粒子群算法作为智能优化算法中的一种,具有易实现、调参少、运行速度快等优点,被广泛接受并运用到各个领域。R.Cheng and Y.Jin提出了一种社会粒子群算法(Social learning PSO,SLPSO),根据随机产生的学习概率不断调整修正项,根据种群平均项修正粒子的位置。Juang等人提出模糊集合理论(Fuzzy Set Thery)应用到粒子群算法中,研究出了自适应模糊粒子群算法(Fuzzy Set Theory,AFPSO)。2012 年Li等人提出了自我学习粒子群算法(Self learning PSO,SLPSO),粒子会在迭代过程中根据当前搜索解的情况从学习策略中选择一种进行自我学习和更新。Ahmad Nickabadi提出了一种自适应性的惯性权重,Kumar 和Chaturvedi设计了一种基于模糊逻辑控制(FLC)并自适应调整的惯性权重。本文采用无需惯性权重学习因素的社会粒子群算法,特别是其不需要对繁琐的算法参数进行确定。
1 蒸发器的工作原理与模型结构
如图1为蒸发器的结构模型。上面的管道模拟制冷剂循环,其内流动的工作介质是制冷剂,描述的是制冷剂相变换热的过程;下面的管道模拟冷冻水循环(以水冷蒸发器为例),其内流动的工作介质是水,描述的是冷冻水显热换热的过程;制冷剂和冷冻水被传热介质隔开,他们之间的能量交换是通过传热介质与两种工作介质的接触面以热传导的形式实现的。在制冷剂循环内,从冷凝器出来的高压低温的液态制冷剂在膨胀阀的节流作用下变为低压低温的气液两相态,进入蒸发器参与换热。由于传热系数的不同,制冷剂在蒸发器内的换热过程通常分为两相区和过热区两部分。在两相区,气液两相态制冷剂不断地通过传热介质从冷冻水中获得能量而不断汽化,直至全部相变为气态,该区域的换热系数较大,其温度为制冷剂的饱和相变温度。从制冷剂全部相变为气态开始,直至蒸发器出口这段区域为过热区,在该段区域内,制冷剂以气态的形式通过传热介质与冷冻水进行换热,换热系数较小,其温度随着从冷冻水内吸收能量的增加而升高,表现为一种过热状态。在冷冻水循环中,冷冻水的能量不断地传递给制冷剂,其温度不断降低。
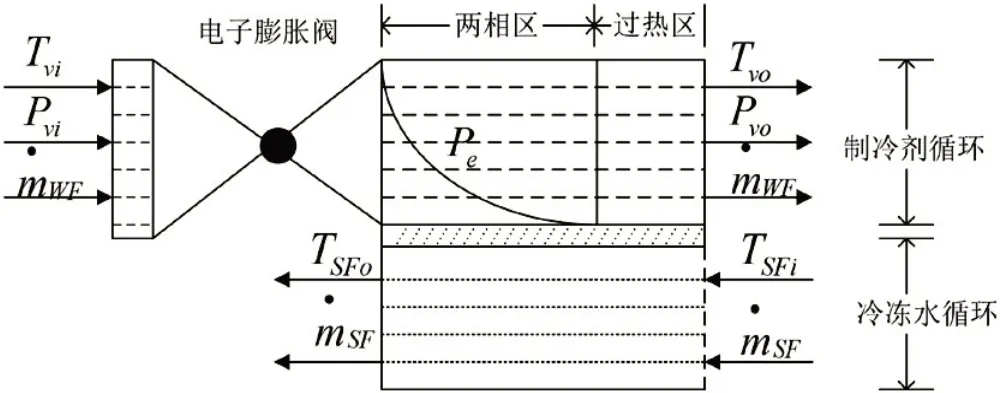
图1 蒸发器原理图
为了验证所提出的参数辨识方法的有效性,本文采用文献所建立的蒸发器热力学混合模型,比较非线性最小二乘和改进粒子群的相对误差与平均相对误差。模型如下式所示:
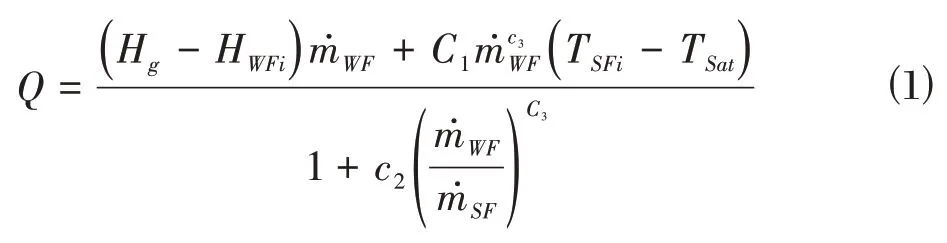

H,H分别为制冷剂的入口焓值和气态饱和焓值,由于蒸发器入口的制冷剂为气液两相态,其焓值无法利用制冷剂的流体特性获得,而蒸发器前的电子膨胀阀的膨胀过程是一个等焓变化过程,没有能量的交换,所以可以利用电子膨胀阀入口制冷剂焓值代替蒸发器入口制冷剂焓值,其值可由制冷剂流体特性拟合的多项式,根据电子膨胀阀入口的制冷剂压力H可由入口温度T和入口压力P计算得出,H可由制冷剂的饱和压力P计算得出,计算公式如下:
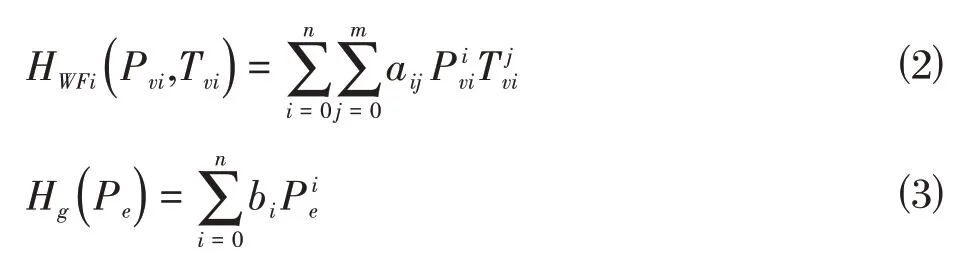
其中,a,b可以通过查表或者离线拟合得出。为蒸发器的总换热率,可通过冷冻水的出入口的温度和流量直接算出,计算公式如下。

其中,T为冷冻水的入口温度,T为冷冻水的出口温度,可以由安装在冷冻水循环出入口处的温度传感器测量获得,c为冷冻水的比热容。由于建立模型的准确与否影响着后续对蒸发器优化与控制研究,所以要运用先进的算法对模型参数进行辨识。
2 辨识方法
假设存在一个非线性模型y=(x |),其中x、y为模型的输入输出观测数据,为模型的参数。对于本文中考虑优化的问题,可以将其转换成最小化问题:
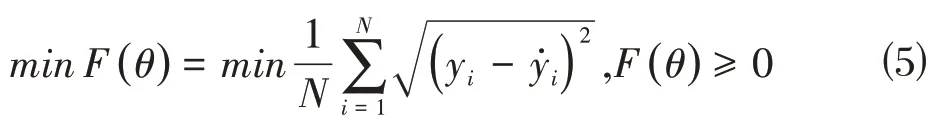
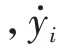
2.1 社会粒子群算法
与普通粒子群相比,社会粒子群除了适应度值的评估,又添加了蜂群的分类和行为学习作为补充。首先根据粒子的适应度值对分群进行分类、排序。然后每一个粒子将从相应的最好的粒子那里学习。任何一个粒子都可以成为不同模仿者的示范者,当然粒子适应度值最差的那个永远不可能成为示范者,粒子最好的那个也不可能成为模仿者(当前蜂群中最好的粒将不会更新)。受社会学习机制的启发,模仿者将从不同的示范者那里学习,利用实验获取数据对蒸发器模型参数辨识具体步骤如下。
与基本粒子群算法初始化一样,社会粒子群先定义一个包含个粒子的蜂群(),每个粒子在()都存在一个随机初始化位置X(),并且每个粒子都有各自的适应度函数值(),随机产生一个学习概率。
计算每个粒子的适应度值,更新粒子的最优解。将粒子的适应度值以降序进行排列,粒子位置更新公式⑹。
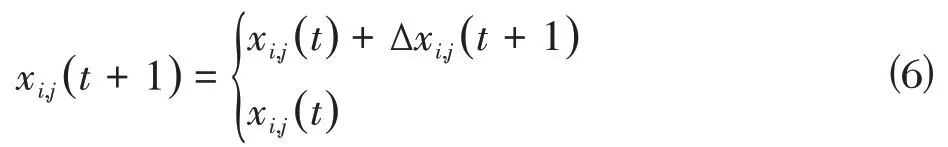
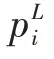

表示为社会粒子群正常工作的基本蜂群大小。
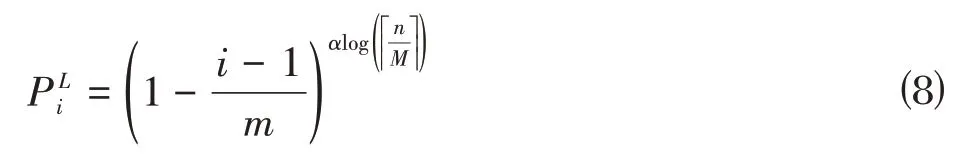
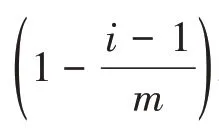

=0.01,如果这个参数值设置过大,可能会出现过早收敛到平均行为的情况。
当随机产生的学习概率低于当前粒子的的学习概率时,该粒子会修正其行为;否则保持不变,修正项为公式⑽:
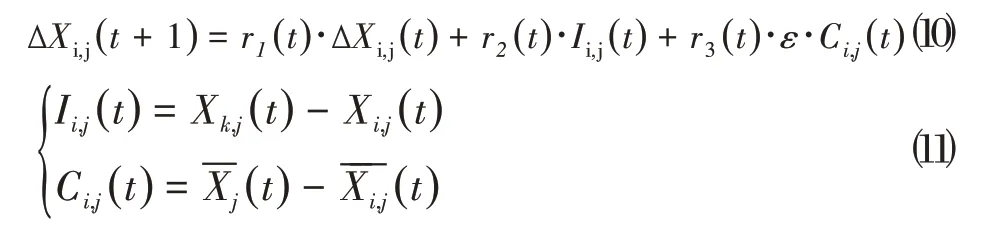
其中,表示蜂群中所有粒子的平均行为,被称为社会影响因素。修正项是由三个部分组成。第一部分()·ΔX()就是基本粒子群算法的位置更新,第二部分()·I()是粒子学习任何比自己适应度值好的粒子,第三部分()··C()从社会方面进行学习。
是否满足终止条件,最大迭代次数、最优解,满足退出循环,否则循环第二步。
上述方法通过社会粒子群对蒸发器模型参数的寻优,获得模型参数带入模型即得到蒸发器的整体模型,而且不会降低模型的精度。
3 模型验证
为了验证蒸发器模型的准确性,本实验数据采用位于山东建筑大学智能建筑实验室的蒸汽压缩制冷系统进行模型的验证。如图2所示蒸汽压缩式空调系统是由压缩机、蒸发器、冷凝器、电子膨胀阀、变频调节泵五个主要部件组成。回路中安装了大量温度压力传感器和流量计。该试验使用的制冷剂R134a。通过485总线上传至上位机Labview实时采集和观察数据。
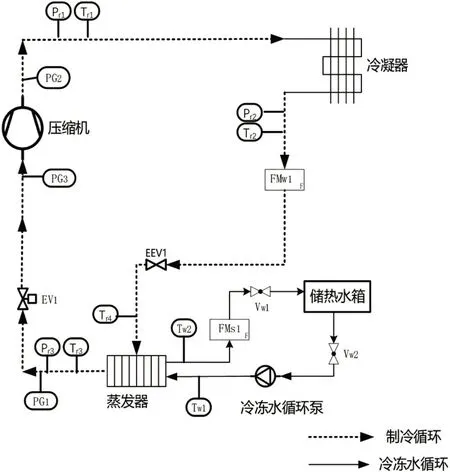
图2 压缩式制冷工艺流程图
室内环境的热负荷通过风机盘管的换热作用进入冷冻水,并在循环水泵的驱动下存储于储水箱;储水箱中的冷冻水存储的能量在循环水泵的驱动下,由冷冻水带入制冷循环的蒸发器;在蒸发器内,冷冻水的能量传递给制冷循环的制冷剂;在制冷循环中,在压缩机做功和电子膨胀阀节流的双重作用下,制冷剂所带有的能量由冷凝器排到室外环境之中,往复运行,达到制冷的目的。实验装置还安装了两个控制器用于控制蒸发器出口的过热度和系统的制冷量。通过调节电子膨胀阀的开度把蒸发器出口的过热度控制在5-10℃,来确保蒸发器的换热效率,同时防止压缩机发生液击现象;当制冷温度达到设定值时,通过调节压缩机的工作频率,改变系统的制冷量,使其与室内热负荷达到平衡,实现系统的变频控制。本文在实验的过程中,为了精确地模拟室内热负荷的各种工况条件,在储水箱中安装了加热器,利用调功器改变加热器的加热量来模拟风机盘管水循环从室内环境中所获得的能量。
3.1 辨识结果分析
本文在采集了1000组数据后,最后把数据分成两组选取187 组中的50 组稳态数据进行训练辨识,另外选取另一种稳定公况的424 组中的50 组数据,进行测试验证。
计算不同方法下的相对误差和平均相对误差:

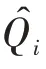
利用本文所获取的稳态数据代入目标函数,使用最小二乘法辨识得到的模型参数为[0.02,0.6,0.7],使用社会粒子群便是得到的模型参数为[0.012,0.4,0.6]。为了验证模型的准确性,把辨识的模型参数代入模型中,将模型的辨识得到的换热量与实测换热量作比较,其结果如图3、图4 所示测试集利用最小二乘、SLPSO拟合数据,为了进一步说明辨识精度,将辨识模型与实测数据分别计算训练相对误差和测试相对误差,结果显示最小二乘与社会粒子群测试集平均相对误差都在±6%,结果如图5、图6 所示最小二乘与SLPSO训练集和测试集拟合误差,训练集混合建模相对误差在±2%以内,测试集混合建模相对误差在±3%以内,说明所辨识的模型能够很好的预测蒸发器的制冷量。
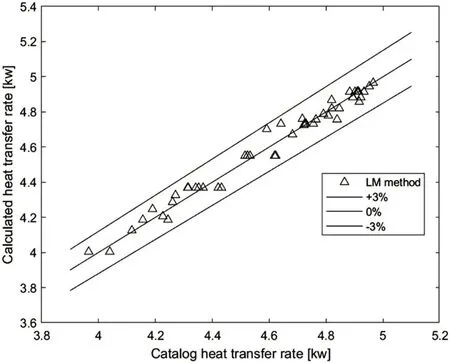
图3 最小二乘测试集预测值与实际值
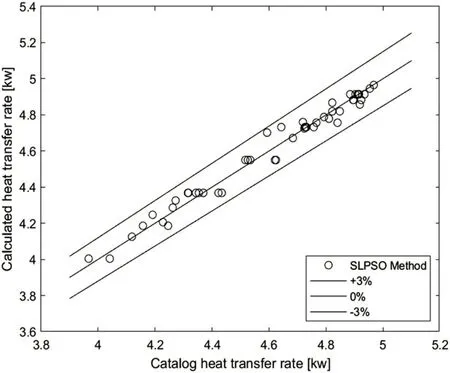
图4 社会粒子群测试集预测值与实际值
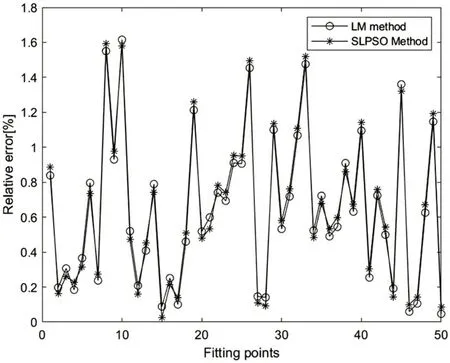
图5 最小二乘与SLPSO训练误差

图6 最小二乘与SLPSO测试误差
4 结束语
针对蒸汽压缩式系统的多变量、非线性、强耦合等特点,本文利用实测数据采用了非线性最小二乘、社会粒子群算法对混合蒸发器模型中的未知参数进行辨识,结果表明社会粒子群算法不但有很高的计算精度还有很快的收敛性,同时避免算法陷入局部最优。实验结果表明利用社会粒子群算法对蒸发器的预测模型辨识误差都在±3%以内,社会粒子群方法获得了很好的预测性能。
本文所运用的社会粒子群参数辨识方法并不仅仅适用于蒸发器的模型的辨识,也同样适用于制冷系统的冷凝器、压缩机、电子膨胀阀等部件,以及其他工业过程部件的建模,其应用前景广泛。

