教育数学指导下的一流课程教材建设——以线性代数为例

王卿文， 张 琴， 杨建生

(上海大学 数学系，上海 200444)

1 教育数学与一流课程建设

长期以来，数学课程的改革主要集中在教学方法方面，即以“自主、合作、探究”的教学理念为主轴进行改革实践，取得了很多成果，对数学教材教法的研究也有了很好的积累. 但是数学难教、数学难学而使许多人望而生畏的现象依然存在.

人们普遍认为，数学创造的活动已经集中在数学发展的前沿，大学本科所学的数学是完全成熟了的定型知识. 这种思维定式导致教学改革仅仅局限于对教材的取舍和教法的改进及测评方式的变化，而没有考虑数学知识本身的改进，这是数学教育长期以来难以破解难教与难学的症结所在. 针对这种局面，张景中院士在他的专著《从数学教育到教育数学》提出了介于数学和教育学之间以数学为主的交叉研究方向——教育数学. 教育数学与数学教育不同但有密切关系：数学教育研究教什么和怎么教，即教材和教法，不承担数学上的创造. 教育数学是以数学教育为目的，为了数学的传承研究数学，对数学的成果进行再创造，改造数学的内容、体系及表述、呈现形式使之更适于教和学及评价. 关于教育数学与数学教育，张院士曾打过形象的比喻：把学习数学比喻为吃核桃，数学教育研究改进砸核桃技巧，教育数学则研究改良核桃品种，使其味更美、营养更丰富，更易破皮吃净.

教育数学的核心思想是“因为教育的需要而研究数学”. 除了把数学变简单，讲明白之外，还研究如何培养学生以下两种能力：将知识、能力、素质有机融合，解决复杂问题的综合能力；运用所学知识研究开放问题，提升学生的研究创新能力.

经过多年的发展与实践，教育数学对解决数学难教和难学问题发挥了重要作用，在国内外产生了重大影响和辐射.

2019年10月底教育部发布了国家一流本科课程建设的基本要求. 明确提出了一流课程建设必须体现高阶性、创新性和挑战度. 从教育数学的理念可以看出，教育数学和国家一流本科课程要求的两性一度是深度融合的，并对一流课程建设具有指导和推动作用.

2 教育数学指导下的线性代数教材建设

教育数学提出了三个任务：对数学研究成果进行数学和教学法两方面的再创造，将数学的原始形态转化为教育形态，变成符合教育规律、容易传承的知识体系；对于已有数学知识在体系结构的简约性和知识传播的有效性上进行再创造，以最简洁明了、易于接受的逻辑体系向学生传授最有价值的数学知识；优化数学知识的表述方式，使得教材更加科学、更加平易，更加符合教育规律.

2020年，作者主持的线性代数课程获批首批国家级一流本科线下课程. 同时，作者也获批中国高等教育学会教育数学专业委员会重大委课题“教育数学与一流课程建设”、高等学校大学数学教学研究与发展中心教改项目“基于教育数学思想的一流课程教材建设”、上海高校本科重点教改项目“创立和发展教育数学理论，重构大学数学课程体系和课程内容”. 在一流课程线性代数建设过程中形成的教材《线性代数》也由高等教育出版社在2022年出版.

下面谈谈作者以教育数学为指导建设《线性代数》教材(以下简称教材)的几点做法和体会.

2.1 基于教育数学思想和任务调整优化线性代数课程体系和内容

基于教育数学的思想及任务，笔者确定了教材编写的指导思想：将线性代数的基本理论和方法，以严谨新颖、深入浅出的形式展现给不同层次的读者，凸显方法简捷、观点高远、趋向前沿、反映现代，力图使教师好教并且学生易学.

教材围绕矩阵的三种重要等价关系——矩阵的相抵、相似和相合展开，先从矩阵的相抵讲起，浓墨重彩矩阵的初等变换、矩阵的分块、矩阵的相抵标准形等重要工具后，直接进入线性代数的主要研究对象——线性空间，将线性方程组作为子空间和矩阵相抵标准形的直接应用，建立简捷的实用解法，之后进入线性变换，聚焦线性变换与矩阵的一一对应，最后着重讨论矩阵的化简——相似与相合.

上述内容顺序和处理方法与传统教材不同，既涵盖了国内现行线性代数课程的所有内容和教学要求，又能在课时较少的情况下，保障学生能够快速进入线性代数的主要研究对象，既好又快地学习和掌握线性代数的核心理论.

2.2 以实现教育数学任务的主要途径建设线性代数教材

提出新定义新概念，建立新方法新体系，发掘新问题新技巧，寻求新思路新趣味是实现教育数学所提任务的主要途径. 以此为指导，在一流本科课程线性代数教材建设中采取了如下卓有成效的措施.

① 着重阐述知识的来龙去脉，引领读者用已有知识和方法去“发现”后面要学习的知识. 每一章节开始，大都介绍要学习知识的由来和动机；从例子入手，概括出一般，引入新概念；从特殊情况出发，发现规律，总结出定理；从读者的角度考虑，尽力使所展现的理论和方法具有新颖性、趣味性和可读性. 譬如，传统教材中线性空间的定义是学生首次接触到的一个拥有两种代数运算、8条运算律的用公理化体系建立的概念. 不少学生不仅对线性空间概念难以理解，就是对向量的加法、数乘两种运算的本质也是一头雾水，更不能理解8条运算律中的第一条加法的交换律不独立(即可由其余7条推出)，但却不能去掉. 为避免上述问题的发生，本教材先从复数和矩阵等的加法及矩阵和多项式的数乘的特征出发，概括出加法和数乘满足的运算律，推广到一般的非空集合和数域，在给出加法和数乘运算定义的基础上简洁地定义线性空间. 具体如下：

集合V中的加法：V×V到V的一个代数运算满足：∀α，β，γ∈V，有

(i) 交换律：α+β=β+α；

(ii) 结合律：α+(β+γ)=(α+β)+γ；

(iii) 有零元素：∀α∈V，α+0=α；

(iv) 每个元素有负元素：α+(-α)=0.

集合V中的数乘：F×V到V的一个代数运算满足：∀k，l∈F，∀α∈V，有

(i) (kl)α=k(lα)；

(ii) 1α=α.

基于定义的集合中的加法和数乘运算，给出线性空间的定义：

定义对于非空集合V和数域F，若V中有加法和数乘运算，且满足分配律：∀k，l∈F，

(i) (k+l)α=kα+lα；

(ii)k(α+β)=kα+kβ，

则称V为F上的一个线性空间，F为V的基域.

上述处理可使读者既能容易理解什么是一般的加法和数乘，又能轻松把握线性空间的定义，避免了初学者很难理解线性空间传统的定义，打消了加法交换律不独立但又不能去掉的疑惑.

② 突出数学思想和方法的运用，力图以简捷方式展现线性代数的核心理论和方法.譬如，矩阵的分块思想、标准单位向量、矩阵的相抵标准形、子空间基的扩充、线性空间的同构、线性变换与矩阵的一一对应关系、对称矩阵的正交对角化等思想和方法在教材中反复运用，力图使这些核心思想和方法成为读者解决应用问题和实践创新的主要利器.

③ 兼顾知识的深度、广度和应用度，以适合不同层次的读者.教材优化了线性代数的课程体系、以简捷明了的方式处理课程内容，在保障课时较少的读者能够学习和掌握线性代数的核心理论外，还在每个章节专门为课时相对较多、学有余力的读者设计和选配了有一定挑战度的例题和习题，同时设计了有一定深度、广度和应用度的“探索与发现”，精选和设计了若干理论探究和应用探索的研究性课题.譬如，二次型是二次齐次多项式，教材在理论探索部分将其作为实对称矩阵的应用，解决了传统线性代数教材以独立章节研究非线性内容所造成的自相矛盾；理论探究的设计重点体现挑战度，比如，利用本教材研究线性方程组的简捷方法研究线性矩阵方程等.应用探索的设计重点体现趣味性和应用度，例如，可逆矩阵应用到密码、线性空间应用到幻方和数列、线性变换应用到数字信号、矩阵的化简应用到汽车租赁等.

④ 突出了线性代数与中学数学的有机衔接与融通.部分线性代数的概念引入从中学数学入口，某些线性代数的重要结论用初等方法证明.例如，类比数的除法引入矩阵的逆，用初等方法证明柯西-布涅柯夫斯基不等式，用一个数是实数的充要条件是这个数的共轭等于自身来证明实对称矩阵的特征值是实数等.教材每章都设计了利用线性代数知识简捷处理复杂初等数学问题的典型例子，比如，用行列式证明不等式、分解因式、解无理方程，用向量的线性关系解无理方程、证明几何问题，用线性方程组解决代数、三角和几何问题，用线性变换求椭圆的面积，用二次型证明不等式等.下面分别举例说明利用行列式解无理方程和利用线性方程组证明等式.

解原方程化为

根据行列式的性质得

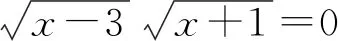
例2已知log157=a，log215=b，log353=c，求证ab+bc+ca+2abc=1.

证由已知可得

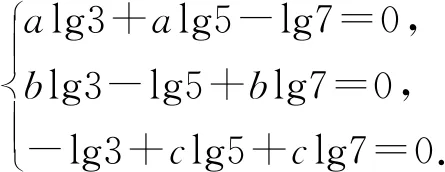
此示，(lg3，lg5，lg7)是齐次线性方程组

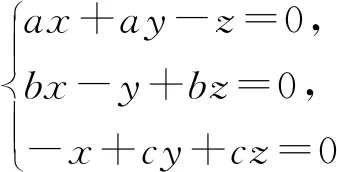
的非零解.故

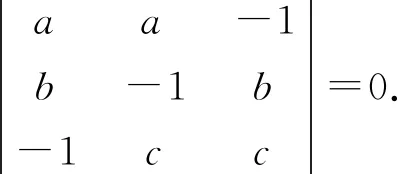
展开上面的行列式即得ab+bc+ca+2abc=1.

⑤ 注重课程思政元素和数学文化的渗透.教材把中国古代数学名著《九章算术》在矩阵、行列式、线性方程组等多个领域中的成就及中国现代数学之父华罗庚有关的内容及课程中相关数学家的贡献自然渗透到教材中，把“观察—抽象—探究—猜测—证明”的科研方法贯穿教材的始终，引导学生探索现代科技背后的数学应用原理，使学生在学习中感受科技发展的巨大魅力，激发学习热情与求知欲，培养其初步的科研意识和实践创新能力.

除上述特点外，教材还与传统教科书兼容并蓄.比如，教材用递归方法定义行列式，也引领读者探索用逆序数给出其定义；用行向量和列向量的形式表示线性方程组，也用行向量和列向量的形式定义矩阵的特征向量.

2.3 以教育数学着眼于难点和新点指导线性代数教材建设

① 教育数学着眼于数学的难点. 难点的产生是由于现有的数学知识对某些客观规律反映得不够好，不适用于教育. 线性代数教材中有诸多难点，使得教师难教、学生难学. 譬如，矩阵的秩、齐次线性方程组基础解系、一般线性方程组的求解、Sylvester惯性定律的证明等等. 针对这些难点，笔者通过优化数学概念的表述方式，寻找更有力、更好学的方法，从根本上化解难点. 譬如，矩阵的分块技巧是以华罗庚为代表的中国代数学家从事科学研究的杀手锏，本教材突显这一思想和方法的巧妙运用，发掘新技巧，创造新办法，给出了矩阵相抵标准形唯一性的简捷证明，从而用矩阵相抵标准形中数字1的个数定义矩阵的秩，不仅准确刻画了矩阵秩的含义——“给矩阵排序”，而且相关理论证明及计算也简单实用；进而用矩阵的相抵标准型，给出了齐次线性方程组解空间的基的简便求法和一般线性方程组的实用解法，并将之用于研究相应的矩阵方程；对矩阵采用不同的分块，给出了Sylvester惯性定律的几种简单证明；又如，一般数域上的方阵可对角化的实用判定定理同类教材大都仅给出此定理而未证明，其原因是传统的证明方法非常复杂，非数学专业的读者很难理解. 本教材给出了一般读者容易接受的简捷证明，保证了教材相关内容的科学性、严谨性和连贯性.

② 教育数学着眼于新点. 科技进步和新业态的出现，高阶知识进入大学数学，成为新内容. 既需要安排推陈出新的知识升级迭代，更需要对知识内容进行宜于教和学的再创造，便于学生将数学知识应用到科技新领域. 如，大数据和人工智能时代的到来，使矩阵奇异值分解在机器学习等众多领域的应用愈加凸显. 传统的线性代数教材甚至数学专业的高等代数教材都不涉及矩阵的奇异值分解. 本教材，对于一般实矩阵A，从构造对称矩阵AA′出发，利用实对称矩阵的正交相似对角化定理，引领学生轻松发现矩阵的奇异值分解定理，使非数学专业的本科生也能掌握其理论并用之解决实际问题.

3 结 论

教育数学的本质就是为教育而改造数学，让数学变简单，使得教师好教学生易学.这就要求对现有课程教材的体系、内容和方法进行卓有成效的改革，使得教学内容体现前沿性、时代性、突出创新性，课程教材设计要体现创新性、研究性和综合性，从而培养和提升学生的创新思维和解决复杂问题的综合能力.因此，教育数学的思想、任务和实现的途径与当前进行的一流课程建设的要求相辅相成.本文以具体实例，介绍了以教育数学的思想、主要任务及其实现的途径为指导，建设首批国家一流本科课程“线性代数”教材的经验做法和体会，期望能给其它学科的教材建设带来有益的启发和借鉴.

致谢作者非常感谢相关文献对本文的启发以及审稿专家提出的宝贵意见.