一种基于分块压缩感知和迂回匹配追踪算法的图像重构方法
王文科, 曹胜芳, 胡红萍
(中北大学 理学院, 山西 太原 030051)
压缩感知(Compressed Sensing, CS)是近年来出现的一种信号采样的新理论, 首先, 对信号进行稀疏表示, 然后, 对稀疏后的信号进行降维, 最后, 通过重构算法对信号进行恢复. 目前, CS已运用到矩阵信号处理、 无线信号通信、 成像、 生物医学传感、 生理信息采集等领域. 基于CS的无线传感器网络可以同时完成数据采样和数据压缩, 大大降低了网络数据的传输量和能耗. Jiang等[1]提出了一种基于CS的动态重传算法 以保证高数据重构精度、 高网络寿命和高能量利用率. 为了克服导波检测数据量大的问题, 保持缺陷识别的准确性, Wang等[2]提出了一种用于导波检测的压缩传感方法, 取得了很好的效果.
当前, 已有许多学者加入到研究CS图像重构的行列中. CS是一种快速磁共振成像(Magnetic Resonance Imaging, MRI)的有效方法. 为了提高重建精度和计算速度, Shohei等[3]提出了一种基于CS的深度学习结构. MR图像重建实验表明, 该方法显著加快了重建时间, 图像质量与传统迭代重建相当. 对于传统的高光谱成像技术, 需要获得大量的高光谱图像(Hyperspectral Image, HSI), 具有数百个光谱波段, 导致数据采集、 传输和存储成本高, W等[4]利用CS提出了一种新的基于上下文的压缩感知(Context-Aware-CS, CACS)方法, 实验结果表明, 该方法优于现有的一些高光谱压缩成像方法. Deng等[5]提出了一种基于CS的迭代贪婪重构算法, 由正交匹配追踪和子空间追踪算法估计的支持集的交集首先被设置为初始候选支持, 然后, 通过贪婪算法的回退和校正, 利用CS进行图像重构. 电阻断层扫描是一种用于过程监控和测量的传感技术, 需要快速准确的图像重构. Zhang等[6]提出了一种改进的正交匹配追踪(Orthogonal Matching Pursuit, OMP)算法, 基于经典OMP算法, 通过增加一个连续约束来防止局部最优解和自适应过程, 该算法基于测量的信息熵寻找最优迭代次数, 使其适用于电阻断层扫描逆问题. 裴廷睿[7]提出了迂回式匹配追踪(Detouring Matching Pursuit, DMP)算法, 实验结果表明, DMP算法计算复杂度较低、 重构精度高、 对传感器矩阵列相关性要求低, 在信号重构精度方面具有明显优势.
本文主要基于离散余弦变换[8](Discrete Cosine Transform, DCT), 使用DMP算法, 解决了传统的基于OMP算法、 BP算法等重构图像计算度复杂, 重构准确率低等问题. 该算法的主要思想是, 先对图像进行分块DCT变换, 然后, 对变换后图像信号再进行分块操作, 变为很多的列向量矩阵, 采用DMP算法进行重构实验. 实验结果表明, 基于分块 DMP算法的图像重构效果相比传统的基于OMP, BP算法都有较大的提升.
1 基本理论
1.1 BCS理论
CS通过有限数量的线性泛函观测感兴趣的未知信号. 这些观测值可被视为相对于给定线性变换T的信号频谱的不完整部分, 因此, 常规线性重构/合成(例如, 逆变换)通常不能重构信号. 例如, 当T是傅里叶变换时, CS考虑的情况是, 可用采样频率远小于奈奎斯特-香农采样理论所需的最高频率. 通常假设信号可以相对于不同的相关基(例如, 小波)稀疏地表示, 或者, 它属于特定的函数类(例如, 分段常数函数). 众多的实验结果表明, 在这种假设下, 未知信号的稳定重建是可能的, 并且在某些情况下重建是精确的[9 -11]. 若x为长度N的一维信号, 稀疏度为K,A为M×N的二维矩阵(M y=Φx=Φψs=Θs, (1) Θ=Φψ, (2) 式中:Θ称为传感矩阵, 求出s的逼近值s′, 则原始信号x′=ψs′. 在CS图像重构研究中, Gan等[15]最先提出了图像分块压缩感知(Block Compressed Sensing, BCS)思想. 基于BCS理论的主要操作是将原始图像分割成许多大小相同的小图像块, 并对这些小图像块使用相同的观测矩阵. 同时, 这些图像块在图像信号重建端被重建以组合整个图像. 图像x, 像素N=Ir×Ic的图像分为很多个B×B大小的图像块.用xi表示第i个图像块,i=1,2,…,n,n=N/B2, 将分块之后的图像, 采用相同的测量矩阵ΦB, 对各个子块xi进行测量, 得到测量值 yi=ΦBxi. (3) 这种分块处理方式相当于对整个图像使用等价的采样矩阵 (4) 整个图像观测值 (5) 各个恢复图像块 (6) 相对于原来的CS方法, BCS分块后测量矩阵ΦB的尺寸会变小, 这不仅使离散余弦变换后的信号更加稀疏, 还减少了存储测量矩阵所用的空间, 计算复杂度降低, 大大提高了图像的重构速度. 从观测矩阵y恢复稀疏信号的问题可以表述为一个L0问题 (7) 该问题被证明是一个NP问题, 通常将其转化为一个L1问题 (8) OMP是一种最简单有效的贪婪重构算法, 它加入与当前残差相关性最大的列向量Φi到子矩阵Φs, 并更新假定支撑集. 由于OMP没有对假定支撑集进行修正, 使得OMP可重构的稀疏信号的稀疏度范围受限. 后来提出的压缩抽样匹配追踪(Compressive Sampling Matching Pursuit, CoSaMP)[16]算法, 通过扩增缩减的方法, 修订假定支撑集, 可以使重构准确率高于OMP算法. DMP算法主要步骤如下: 步骤2: 得到一个原始的假定支撑集S (9) 步骤3: 逐个缩减支撑集元素 (10) 步骤4: 逐个扩增支撑集元素 (11) 步骤5: 循环步骤3和步骤4, 直至满足设定条件, 跳出循环, 输出正确的支撑集S*和稀疏信号x.其中全集Ω={1,2,…N}, 子集S∈Ω,i∈S表示i在集合S中的位置. 首先, 对原始图像进行DCT稀疏变换; 其次, 将变换后的稀疏图像信号均匀分块, 将每个子块图像数据转换成列矩阵, 使用相同的观测矩阵观测采样这些图像子块, 并将采样得到的信号转换成列矩阵, 再利用DMP算法循环重构每个小图像块对应的列矩阵, 将重构信号进行DCT逆变换, 得到重构图像; 最后, 采用3×3的窗口模板对重构图像进行均值滤波,实现平滑去噪. 由此, 建立了基于BCS和DMP的图像重构算法, 记为BCS-DMP. 具体算法流程如下: 步骤1: 输入原始图像信号, 对原始图像进行一次中值滤波预处理; 步骤2: 使用DCT变换稀疏信号, 对输入信号按每个8×8的分块大小处理, 进行DCT变换, 建立一个8×8的mask矩阵来保留不同数量和部位的DCT系数, 块重构得到稀疏信号及稀疏度; 步骤3: 将像素为256×256的图像均匀分块处理,设置各分块图像si的大小均为16×16, 其中i=1,2…16, 把所分大小为16×16的块矩阵s转化为si=256×1的列矩阵; 步骤4: 选取合适的M值,生成M×256维的高斯随机测量矩阵, 对si进行测量, 得到测量矩阵yi, 其中M=τ×256(M取整),τ为压缩比; 步骤5: 利用DMP算法对列矩阵进行信号重构, 并把重构信号列矩阵进行保存. 步骤6: 将重构后的列矩阵转化为块矩阵并进行DCT逆变换, 直到对所有小块图像si压缩重构完毕,进而重新按照顺序组合成整幅图像, 并对得到的图像进行均值滤波, 使得到的图像更加平滑. 本文提出的BCS-DMP算法实现图像重构的流程图如图 1 所示. 图 1 BCS-DMP图像重构 采用3种经典测试图像: Camera, Peppers, Boats(图像大小为256×256像素), 选用配置为 intel(R) Core(TM) i5-7300HQ, 2.50 GHz, 8.00 GB内存的计算机, 在Matlab R2019b环境中进行实验. 算法重构性能用峰值信噪比(Peak Signal to Noise Ratio, PSNR)衡量, PSNR公式为 (12) (13) 式中:MSE为图像x和图像y的均方误差;H,W分别为图像的高度和宽度;n为每个像素的比特数, 一般取8. 采用CS_OMP, CS_BP, CS_Bayes, CS_CoSaMP, CS_SP与本文提出的BCS-DMP算法进行对比实验, 这6种算法都是在基于离散余弦变换的基础上进行重构. 在压缩比τ分别为0.2,0.3,0.4,0.5的情况下, 这6种算法的峰值信噪比的比较由表 1 所示. 表 1 在不同压缩比τ下4种算法的峰值信噪比比较 在表 1 中, 当τ=0.3,0.4,0.5时, 本文提出的BCS-DMP算法重构信噪比均达到最高, 分别为25.48 dB, 26.90 dB, 27.53 dB(Camera), 26.35 dB, 27.82 dB, 28.25 dB(Peppers)和26.63 dB, 28.23 dB, 29.53 dB(Boats). 当τ=0.2 时, CS-BP算法得到Camera和Peppers的峰值信噪比达到最高, 但与本文提出的BCS-DMP算法Camera重构的峰值信噪比相差无几, 而CS_CoSaMP算法的Boats重构图像的峰值信噪比达到最大, 但也是较高于BCS-DMP算法. 说明了BCS-DMP算法优于CS-OMP, CS-BP, CS-Bayes, CS_CoSaMP和CS_SP算法. CS_CoSaMP算法在压缩比τ=0.2时可以达到一个较好的峰值信噪比, 随着压缩比的提高, 峰值信噪比先降低后升高. 除CS_CoSaMP算法外, 剩下几种算法的图像重构的峰值信噪比值随着压缩比的不断提高而不断增大, 提高了图像重构质量. 图 2~图 4 分别为τ=0.5时, Camera, Peppers, Boats的6种算法的重构图像. 从图 2~图 4 可见, BCS-DMP算法的重构效果最棒, 更接近于原图像. 图 2 Camera重构图像 图 3 Peppers重构图像 图 4 Boats重构图像 算法处理时间的对比, 在一定程度上反映了算法复杂度的差别, 为了进一步比较不同算法的重构效果, 进行算法运行时间比较的实验. 如表 2 所示, 当τ=0.5时, 通过6种算法, 分别对Camera, Peppers, Boats进行10次实验, 取其均值, 得到每组实验运行所需时间. 由表2中数据可知CS_OMP, CS_SP, CS_CoSaMP与BCS-DMP重构时间都较短, 其中CS_SP的重构时间最短, BCS-DMP次之, 但CS_OMP, CS_BP, CS_CoSaMP算法重构效果都不如BCS-DMP算法, CS_BP重构效果仅次于BCS-DMP, 但重构时间是BCS-DMP的5倍~6倍, 进一步说明了本文提出的BCS-DMP算法优于其他5种算法, 且BCS-DMP方法不仅降低了计算复杂度, 而且不需要传输所有的观测数据, 减少了传感器部分的存储量, 加快了重构速度, 并且该算法能准确地重构稀疏度更高的稀疏信号. 表 2 算法运行时间比较 针对图像重构计算度复杂, 重构准确率不高的问题, 本文介绍了一种BCS-DMP算法. 其中, DMP算法采用了先最优逐个缩减、 后最优逐个扩展假定支撑集的思想, 降低了重构稀疏信号的计算复杂度, 提高了重构精度. BCS可以提高离散余弦变换的稀疏效果, 减少存储测量矩阵占用的空间. 实验表明, 本文算法在保证图像重构精度的基础上, 缩减了重构所需时间, 具有一定的实用价值.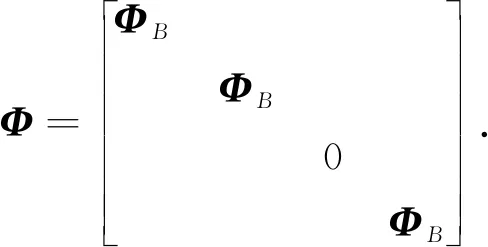
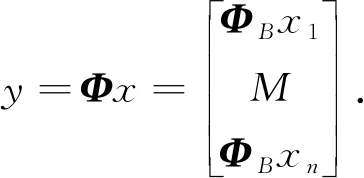

1.2 DMP理论
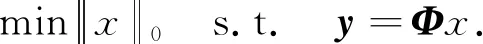
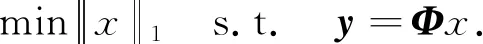
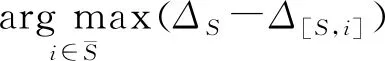
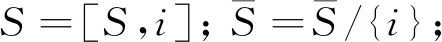
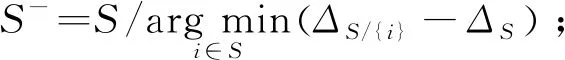

2 基于DMP和BCS的图像重构算法
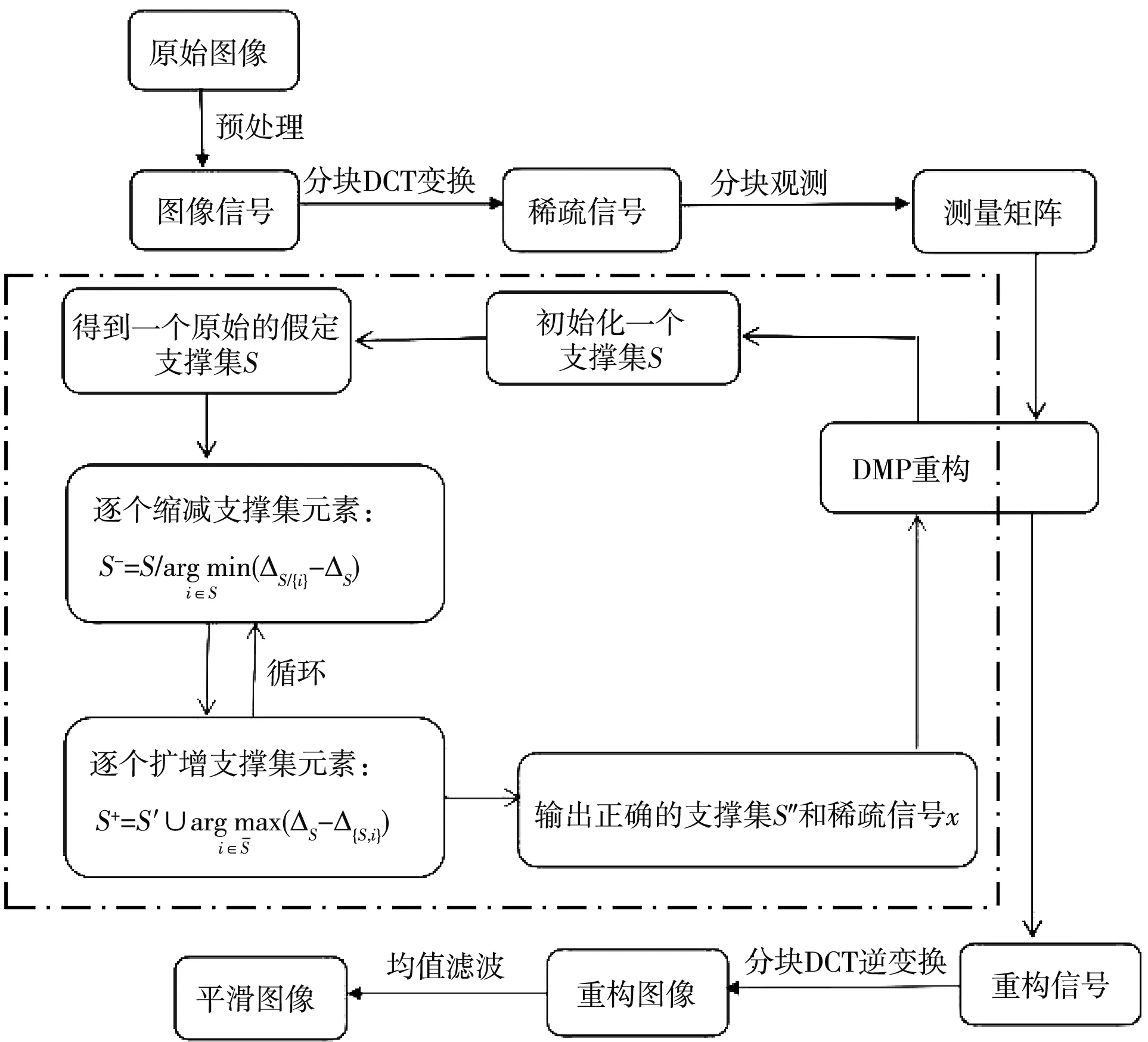
3 实 验







4 结 论

