基于迁移学习的运动想象脑电信号分类研究

冯 洋， 乔晓艳

(山西大学 物理电子工程学院， 山西 太原 030006)

0 引 言

脑-机接口(Brain Computer Interface， BCI)技术为有严重运动障碍的患者提供一种与外界交流的新途径[1]， 在康复医学、 军事、 娱乐等领域都有重要的应用价值. 运动想象BCI通过识别大脑想象动作意图， 来实现与外部设备的交互和控制. 2012年， 浙江大学将96个电极芯片植入健康猴子的大脑皮层中， 采集该猴子在做各类运动时大脑皮层的有效电信号， 进而控制了无意识的机械手动作[2]； 2021年， 埃隆·马斯克旗下的神经科学公司Neuralink， 利用脑机接口技术， 让一只猴子能够在没有游戏操纵杆的情况下， 仅用大脑意念来控制电脑屏幕上的乒乓球拍， 实现接球等动作. 虽然运动想象BCI已经取得了许多成果， 但还存在训练时间较长和泛化能力差等一些问题. 迁移学习是目前脑机接口中解决上述问题比较有效的方法， 旨在从其他被试的辅助样本中获取信息来帮助目标被试的训练， 适合解决目标域训练样本少且域间数据分布差异较大的问题. 根据迁移信息的不同， 可以分别在样本、 特征、 模型以及关系这4个方面进行迁移. 当前， 迁移学习已经成功地应用于文本、 图像和人的行为分类中， 但是对于运动想象脑电信号， 还需要进一步探索其有效性[3].

Ibrahim等[4]将主动学习与直接迁移学习相结合， 选出其他被试中信息量较大的样本添加到目标被试的训练集中， 在BCI竞赛IV多类运动想象数据集上使用， 平均减少了75%的训练数据， 可以达到运动想象两分类的基本性能. 该方法对训练数据的需求减少到了可观的数量， 有效缩短了训练时间； 共空间模式(Common Spatial Patterns， CSP)是运动想象脑电分类中较为有效的一种空域特征提取方法， 但是， 该方法在样本数量较少时， 所估计的协方差矩阵方差较大， 很多研究人员使用迁移学习的思想来改进CSP算法， 以解决上述问题. Ahmed等[5]基于Kullback-Leibler散度的相似性度量方式， 使用共空间模式， 获得两个特征空间之间的相似性， 在BCI Competition Ⅲ数据集上得到平均分类正确率为75%； Haiping Lu等[6]提出的正则共空间模式(Regularized Common Spatial Patterns， RCSP)算法， 利用目标被试和其他被试的脑电数据共同构建正则化协方差矩阵， 解决了CSP方法引起的协方差矩阵估计方差大的问题， 该方法的平均分类正确率比CSP方法提高了8.5%； Kai等[7]在RCSP的基础上， 提出了一种基于动态时间规整(DTW)和迁移学习的CSP正则化协方差矩阵估计框架， 使用DTW进行时间比对， 使得其他被试的样本与目标被试的少数训练样本更相似， 不足之处是DTW的计算复杂度较高.

现有的迁移学习方法大都只在样本、 特征和分类器中的一个方面进行迁移学习， 仅在样本上迁移势必会忽略特征中隐藏的有效信息， 仅在特征上迁移也无法考虑到某些不适合迁移的样本所带来的影响. 本文同时考虑样本和特征两个方面， 提出一种欧几里得对齐-正则共空间模式(Euclidean Alignment-Regularized Common Spatial Patterns， EA-RCSP)的联合迁移学习算法. 首先， 通过欧几里得对齐方法， 使得不同被试的样本分布更相似， 同一被试样本分布更均匀； 然后， 同采用正则化改进共空间模式方法， 通过正则化减小协方差矩阵估计的方差， 利用来自其他被试的辅助样本获取有效信息， 提取出更鲁棒的特征信息. 本文提出的EA-RCSP迁移学习方法， 能够在小样本情况下， 针对单个被试， 有效提升分类正确率； 同时， 模型在不同被试的混合数据样本上也表现出较好的性能， 获得较高的分类正确率和泛化性能， 减小了个体差异对运动想象脑电分类的影响， 为模型的跨用户使用奠定良好基础.

1 算法原理

1.1 正则共空间模式

CSP是一种有监督空间特征提取和分类算法， 被认为是运动想象任务最有效的特征提取算法之一. 其基本方法是： 首先， 通过两类协方差矩阵的同时对角化， 提取两种任务的空间特征， 然后， 构建空间滤波器， 最后， 通过空间滤波使两类信号方差差异最大化， 从而实现两类信号的分类[8]. CSP使用了基于样本的协方差估计， 当样本量较小时， 估计的参数会非常不稳定， 导致高方差. 此外， EEG信号的低信噪比也容易导致CSP估计方差增大.

CSP算法中第c类样本的平均协方差矩阵计算公式为

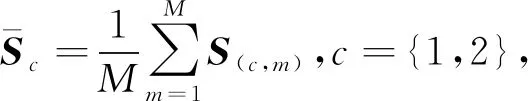
(1)

式中：M为类别c的样本数；m为某个样本，c={1，2}，m=1，…，M， 故某个样本的协方差矩阵可以表示为S(c,m).

正则化是一种用于构建鲁棒模型的非常有效的机器学习方法[9]. 它减少了与样本估计相关变量的方差， 同时倾向于增加偏差. 偏差和方差的权衡通常由一个或多个控制偏差强度的正则化参数来调节. 文献[6]采用正则化方法， 减小协方差矩阵估计的偏差， 提出了基于迁移学习的特征提取算法RCSP. 该算法中类别c的正则协方差矩阵计算如下

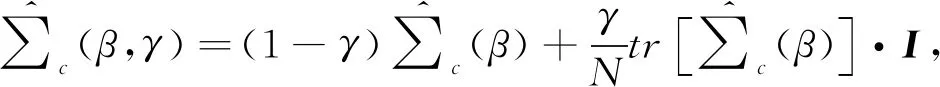
(2)

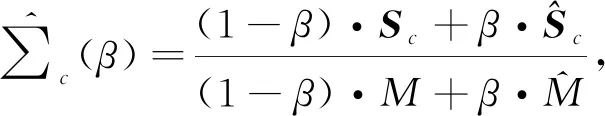
(3)

对比式(1)和式(2)， 不同之处在于CSP只利用目标被试的数据计算协方差矩阵， 而RCSP则是通过正则化方式调整目标被试数据和其他被试数据的比重， 若正则化参数选取合适， 理论上可以得到更为通用的协方差矩阵， 以解决CSP方法因数据量小而引起协方差矩阵估计方差大的问题.

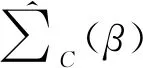
1.2 欧几里得对齐

RCSP迁移方法主要是针对特征空间作处理， 未考虑到不同被试样本数据的分布差异. Dongrui Wu等[10]提出一种无监督的基于样本的迁移算法——欧几里得对齐(EA)， 基本思想是， 使来自不同被试的数据分布更加相似， 因此， 在辅助数据上训练的分类器将会在目标域数据中表现得更好. 由于被试间的个体差异较大， 不同被试的EEG数据， 其边缘概率分布有很大的不同， 故将不同被试数据对齐， 使得其数据分布更一致， 将有助于更好的迁移. EA进行数据对齐过程如下：

假设1名被试有n个数据样本， 首先， 计算该被试的参考协方差矩阵的算术平均

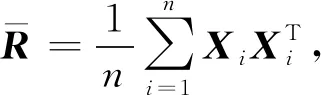
(4)

然后， 按照式(5)进行对齐

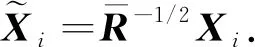
(5)

对齐后， 1名被试所有n个样本的平均协方差矩阵等于单位矩阵， 因此， 不同被试的协方差矩阵分布会更类似， 这将有助于将源域数据中有效信息迁移到目标域.

与其他基于样本的迁移学习方法不同， EA算法没有通过构建分类器来选择相似样本， 故在对齐之后， 依然可以在特征上进行迁移来进一步提升分类效果.

1.3 欧几里得对齐-正则共空间模式

上述两种算法中， 欧几里得对齐仅在训练数据样本上进行迁移， 忽略了源域数据特征所隐藏的有效分类信息； RCSP方法仅在协方差矩阵特征层上实现迁移， 由于脑电数据个体差异较大， 辅助源域和目标域的样本数据分布并不完全一致， 这样会导致特征迁移效果变差甚至失效. 本文提出一种联合迁移学习方法——欧几里得对齐-正则共空间模式. 该方法的流程图如图 1 所示.

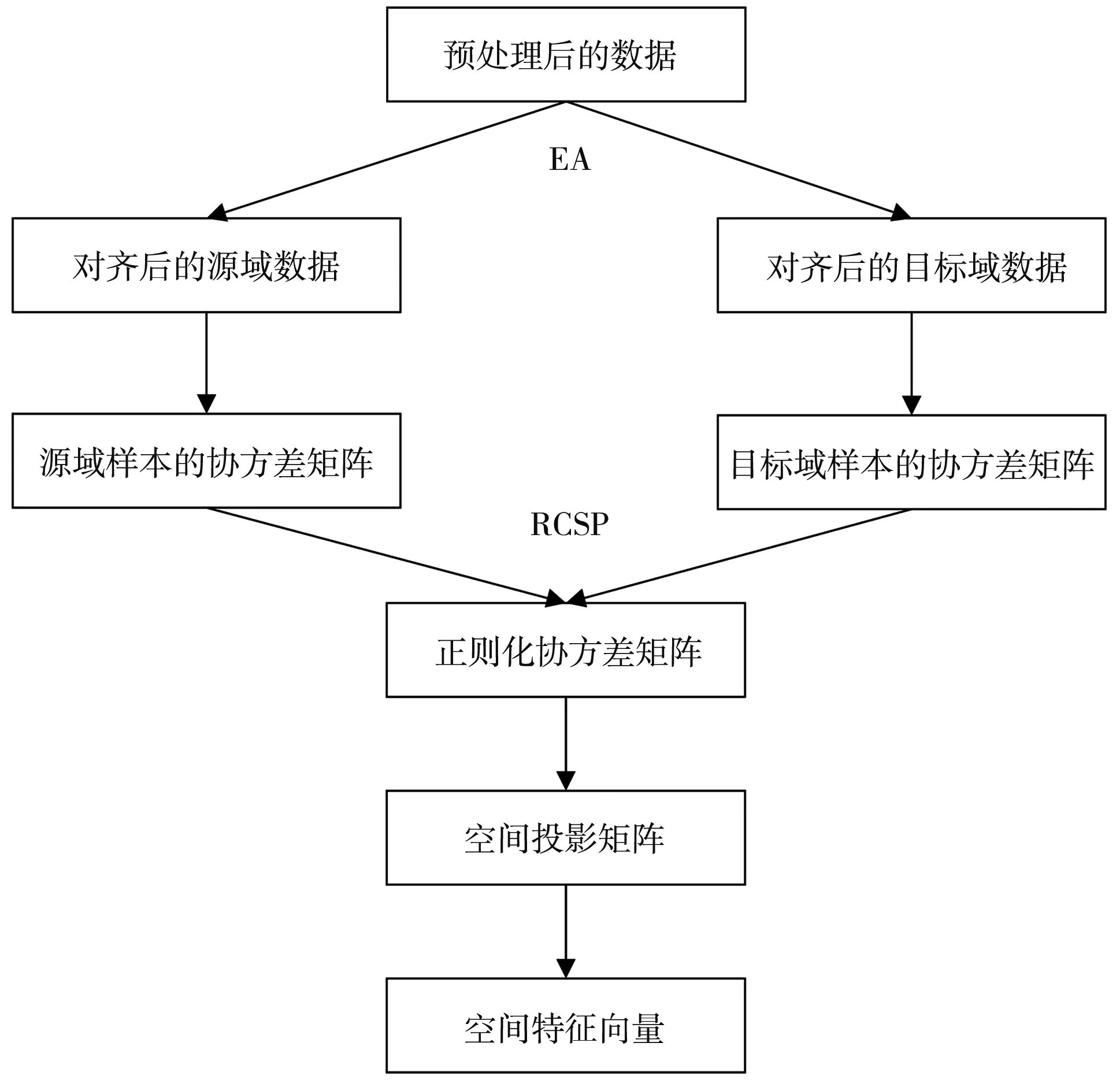
图 1 EA-RCSP方法流程图

EA-RCSP迁移学习方法首先使用EA算法将预处理后的不同被试数据分别进行对齐， 使得被试之间的数据分布更为相似， 这有助于从源域数据中迁移有效信息到目标域. 随后， 采用正则化方法， 通过对齐后的源域和目标域样本数据， 计算得到正则化协方差矩阵， 再通过正交白化变换， 并同时对角化两类样本的平均协方差矩阵， 计算得到投影矩阵. 最后， 将原始数据在高维空间上投影， 得到空间特征向量.

本文所提出的EA-RCSP迁移学习方法， 同时在样本和特征两个方面迁移， 充分利用了辅助被试的脑电数据信息来帮助目标被试实现运动想象脑电分类. 通过数据对齐得到了分布更相似的样本数据， 通过正则化方法， 获得更鲁棒的空间特征. 既减小了域间数据分布差异， 又克服了CSP方法存在的协方差矩阵估计方差大的问题.

2 实验数据来源及预处理

本文采用BCI Competition Ⅲ数据库中的Ⅳa数据集， 该数据集可以用来验证小样本学习方法， 它是由Klaus-Robert Muller的智能数据分析组与Gabriel Curio的神经科学小组等多个科研机构提供的. 该数据集包含aa, al, av, aw, ay 5名健康被试的运动想象脑电数据. 实验开始， 被试坐在舒适的椅子上， 根据屏幕提示执行左手、 右手以及右脚的运动想象任务， 视觉提示下的运动想象过程持续3.5 s， 任务之间的间隔时间为1.75 s～2.25 s. 视觉刺激有两种类型：

1) 用固定十字后面的字母(L， R， F)表示运动想象目标.

2) 用随机移动的物体表示运动想象目标.

该数据集记录了118个导联的脑电信号， 采样频率为100 Hz， 脑电信号进行了 0.5 Hz～200 Hz 的带通滤波. 数据集仅提供了每名被试相同数量的右手和右脚的EEG数据， 共280次实验. 因此， 本文研究的是右手和右脚运动想象的二分类问题. 数据集给出的5名被试的训练样本数量和测试样本数量如表1所示， 其中ay被试的训练样本数量很少， 属于小训练样本.

表 1 数据集描述

大脑在进行单侧运动想象时， 对侧感觉运动皮质脑电信号中的μ节律(8 Hz～12 Hz)和β节律(13 Hz～30 Hz)幅值减小， 频带能量下降， 这种生理学现象称为事件相关去同步化(Event-related Desynchronization， ERD). 同时， 同侧的脑皮质信号中的μ节律和β节律幅值增大， 频带能量上升， 称为事件相关同步化(Event-related Synchronization， ERS)[11]. 当大脑想象不同部位运动时， 大脑皮层对应区域的ERD/ERS现象会存在明显差异， 利用这些差异能有效实现运动想象脑电信号区分， 从而获知被试的运动意图. ERD和ERS现象主要发生在脑电的μ节律和β节律上， 故本文对原始数据集进行了7 Hz～30Hz带通滤波， 在消除高频噪声、 肌电伪迹和直流漂移等干扰的同时， 获得μ节律和β节律的脑电信号. 由于被试从接收想象任务提示到开始想象需要短暂时间， 故本文截取0.5 s～3.5 s的运动想象脑电数据分析处理.

3 运动想象脑电分类算法实现

在对BCI竞赛数据进行上述预处理后， 获得了有效且纯净的运动想象脑电信号； 采用本文设计的EA-RCSP迁移学习方法提取运动想象脑电特征； 利用线性判别分类器， 实现右手和右脚的运动想象任务分类. 为了探究EA-RCSP迁移学习方法的有效性， 在相同数据集和被试上， 分别采用CSP, EA-CSP, RCSP 3种方法实现运动想象脑电特征提取和分类， 并对比分析4种方法的运动想象任务分类效果.

通过仿真测试， 当CSP与RCSP中的公共参数——滤波器对n取3时， 运动想象分类正确率最高， 故本文取n=3作为该参数的默认值.为了找到正则化参数β和γ的最优值， 模型训练时， 令β=[0：0.1：0.9]，γ=[0：0.1：0.9]， 遍历β和γ参数的取值， 寻找最好的分类结果所对应的β和γ值， 作为RCSP模型最优的β*和γ*[6].

在单个被试的训练过程中， 目标域为该名被试的样本数据， 源域为数据集中其余4名被试的样本数据.

将运动想象脑电提取得到的前两维特征用二维散点图可视化， 如图 2 所示. 其中， 横、 纵坐标分别表示两个维度特征的数值大小， 图2(a), (b), (c), (d)分别对应CSP, EA-CSP, RCSP, EA-RCSP方法提取的特征数据， 其中“·”为源域特征， “+”为目标域特征. 从图2(a)可以看出， 仅通过CSP方法提取出的特征， 其源域和目标域的分布存在较大差异， 故在源域数据上训练的分类器不能直接用于目标域； 从图 2(b)～图 2(d) 可以看出通过EA和RCSP， 均可以减小源域和目标域之间的域方差， 经过EA-RCSP方法后， 源域和目标域特征分布最为接近， 由该源域特征训练出的分类器可以有效用于目标域， 表明EA-RCSP方法可以有效减小域间分布差异， 这将对目标域特征的分类效果有很大提升.

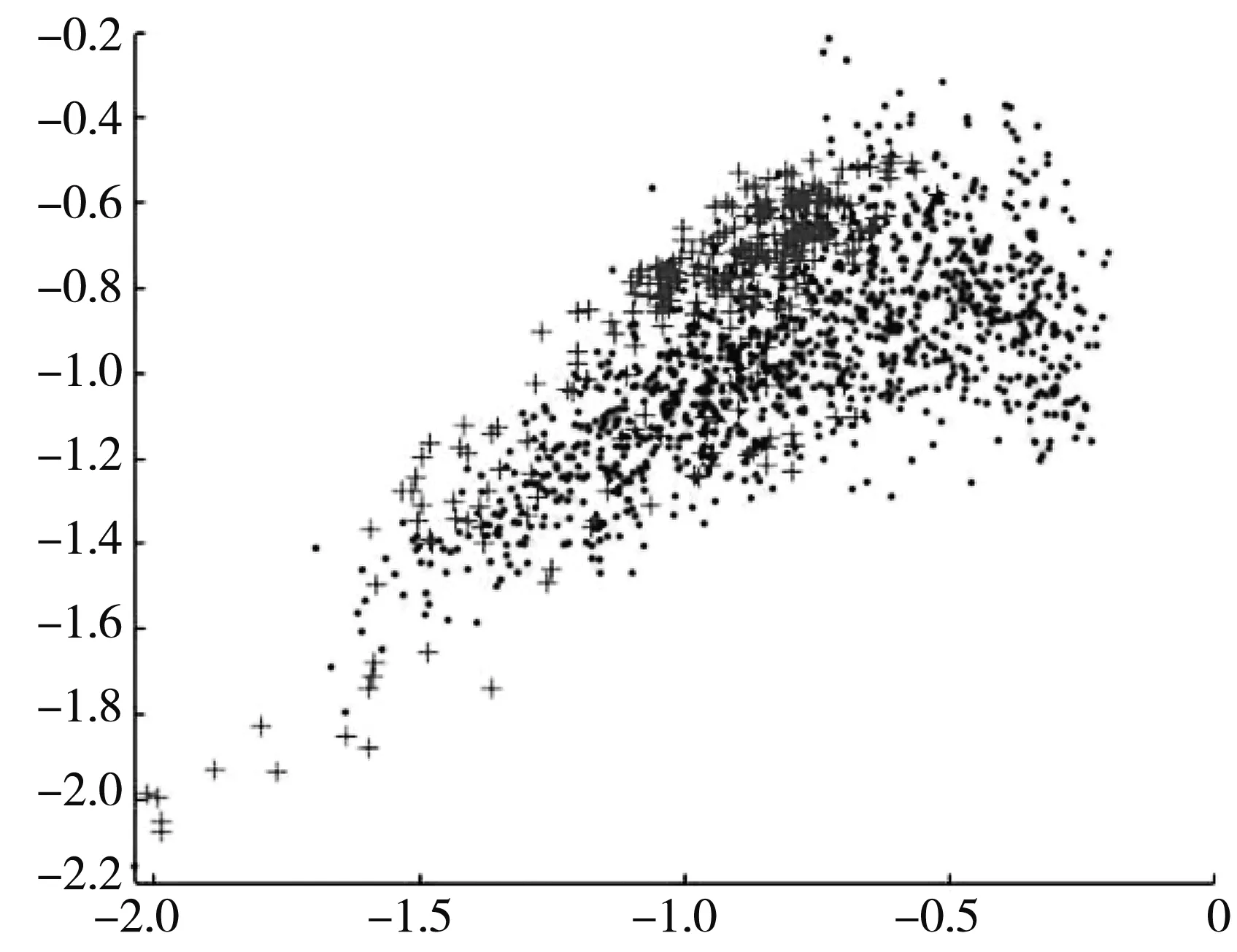
(a) CSP

4 实验结果与分析

4.1 不同方法分类结果比较

分别使用CSP， EA-CSP， RCSP， EA-RCSP4种方法进行运动想象脑电特征提取， 其中， CSP作为基本方法， 其他3种方法是在此基础上的改进. 不同被试的运动想象任务分类正确率如表 2 所示.

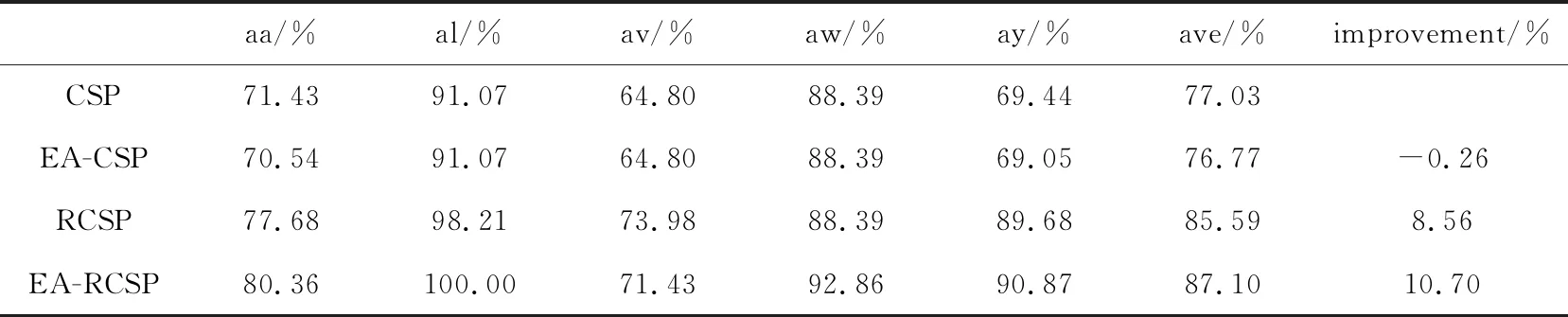
表 2 运动想象脑电分类正确率

表 2 显示了aa， al， av， aw， ay 5名被试在4种不同方法下的分类正确率以及平均正确率. 可以看出， 采用EA方法改进后， 运动想象脑电的平均分类正确率基本无变化， 分类效果没有提升. 这是由于， 在该BCI竞赛数据集中， 虽然5个被试之间的数据分布差异较大， 但单个被试的数据样本分布非常接近， EA改进前后变化不大； 单独使用RCSP迁移学习改进算法， 5名被试的平均分类正确率为85.59%， 相对于CSP方法有较好的提升； 结合EA和RCSP两种迁移算法改进效果最好， 平均分类正确率可以达到87.10%， 相较于CSP算法提高了10.7%， 而且针对每一个被试， 分类正确率均有不同程度的提高， 特别是对于小样本的被试ay， 分类正确率提高了21.43%， 表明该方法非常有助于提升小样本的单个被试的运动想象任务分类效果.

混淆矩阵可以用来评价模型的分类性能， 它由模型测试结果与真实类别进行比较而得， 可以反映模型分类的正确率、 精确度、 召回率和F1指数，F1指数是模型精确率和召回率的一种调和平均.正确率、 精确率、 召回率和F1指数计算方法为

正确率

(6)

精确率

(7)

召回率

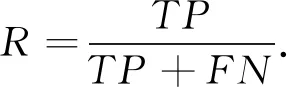
(8)

F1指数

(9)

式中：TP，TN分别表示被正确分为正类或负类的样本个数；FP，FN表示被错误分为正类或负类的样本个数. 以被试ay为例， 画出EA-RCSP方法的分类器混淆矩阵， 如图 3 所示.

图 3 EA-RCSP方法的分类器混淆矩阵

图 4 为分别采用CSP， EA-CSP， RCSP， EA-RCSP 4种不同方法， 被试aa运动想象任务分类的正确率、 精确率、 召回率以及F1指数.

图 4 被试aa在4种方法下的正确率、 精确率、 召回率以及F1指数

从图 4 可以看出EA-RCSP方法的正确率、 召回率、F1指数均达到最高， 虽然EA-RCSP方法的精确率略低于CSP方法， 但其它3个指标均远远高于CSP方法. 由此可见， 本文提出的EA-RCSP方法进行脑电运动想象任务分类， 其分类模型的性能可以达到最好.

4.2 不同训练样本数量的分类结果比较

为了探究所提出的EA-RCSP方法对不同训练样本数量的分类效果， 特别是小样本分类的优势， 将数据集进行如下划分： 从竞赛数据集每名被试的280个样本中， 随机选取20， 60， 140个样本作为训练集， 其余样本作为测试集. 分别采用CSP和EA-RCSP两种方法， 运动想象任务的分类结果如表 3 所示. 为了减小由于一次随机选取训练样本集而引起的偏差， 实验采用了 5次随机选取训练样本进行想象任务分类， 将 5次的分类结果取平均值作为最终的结果.

由表 3 可以看出， 不论训练集的样本数量多或少， EA-RCSP方法都对分类正确率有一定提升. 特别是在训练样本数较少时， 分类正确率提升效果非常显著. 训练样本数为20时， EA-RCSP方法相对于CSP， 5个被试的分类平均正确率提升了14.43%， 这表明EA-RCSP方法更适合于小样本分类， 能够较好地解决由训练样本少而导致分类效果差的问题， 同时可大大缩短模型的训练时间.

表 3 不同训练样本数量分类正确率

4.3 跨被试迁移学习分类结果比较

由于运动想象脑电信号个体差异较大， 脑电数据难以复用， 故不能得到一种适合所有被试的通用模型， 实际中需要进行模型校准和针对个体的大量训练. 为了探究EA-RCSP迁移学习方法在不依赖个体场景下的运动想象分类性能， 将竞赛数据集中5名被试的所有样本数据混合， 随机选取其中的280个样本作为目标域数据， 剩余样本作为源域数据， 并且目标域样本的前140个为训练集， 后140个为测试集， 分别采用CSP方法和EA-RCSP迁移学习方法， 实验进行了5次随机选取样本， 结果如表 4 所示.

表 4 跨被试迁移学习分类正确率

从表 4 中可以看出， 将所有5名被试的脑电数据混合， 随机选取训练样本， 采用EA-RCSP迁移学习方法的分类正确率可以达到87.57%， 比没有使用迁移的CSP方法提高了23.5%， 混合被试训练模型的分类结果与相同训练样本数量下针对单个被试训练的模型分类效果(88.34%)接近. 实验结果表明： 本文提出的EA-RCSP迁移学习方法可以较好地实现不依赖被试(跨被试)的运动想象脑电分类.

4.4 与其他文献方法结果比较

为了验证本文所提出的迁移学习方法的优越性， 对比了文献中采用相同数据集不同迁移学习方法的结果， 分别是平稳子空间共空间模式(ssCSP)[12]、 加权源用户正则共空间模式迁移学习(RCSPTLw)[13]、 迭代的余弦相似度正则共空间模式(iRCSP-CSW)[14]. 其中， 平稳子空间共空间模式利用了其他被试训练集和测试集之间的变化， 减少了目标被试训练集和测试集之间数据分布的不同； 加权源用户正则共空间模式使用佛罗贝尼乌斯范数度量源用户和目标用户平均空域协方差矩阵的差异， 得到了加权平均空域协方差矩阵； 迭代的余弦相似度正则共空间模式采用余弦相似度度量迁移前后空间滤波器的变化， 并以此设置不同源域用户训练样本的权重. 不同算法的分类正确率如表 5 所示.

表 5 不同算法分类正确率

由表 5 可以看出， 本文EA-RCSP方法在aa， al， av， aw 4个被试的分类正确率均高于文献中的 3种迁移学习方法， 对于ay被试， 本文方法与iRCSP-CSW方法比较接近， 但高于其它两种方法. 对于5个被试的平均分类正确率， 本文方法最高. 由此表明EA-RCSP迁移学习方法对运动想象脑电分类的有效性和优越性.

5 结束语

由于运动想象脑电样本数量的限制， 使用CSP方法所得到的协方差矩阵有较大的方差， 而协方差矩阵的波动对CSP特征有很大的影响， 导致训练集和测试集的特征出现较大差异， 从而影响运动想象任务的分类结果. 此外， 由于不同个体的脑电数据分布差异较大， 其他被试的样本数据无法直接用于目标被试， 故需要较长的训练时间来为每个被试训练针对性的模型. 本文提出的EA-RCSP迁移学习方法同时在样本和特征两方面进行迁移， 一方面通过数据对齐方法， 减小域间数据分布差异； 另一方面， 利用正则化的方法， 减小了CSP协方差矩阵估计的偏差. 仿真实验结果表明， EA-RCSP方法可以在小样本训练数据上明显提高每个被试的运动想象脑电分类正确率， 缩短了训练时间， 同时也可以减小不同被试之间的个体差异， 提高模型泛化能力.