中欧班列智能化运输调度策略研究
文/郭蓉 赵海峰
本文从考虑不同节点城市的货物资源分配的角度对中欧班列智能化运输问题进行模型的建立,结合各节点城市主要货源和中欧班列运输资源进行调度优化,利用优化算法选择出在时间窗和班列车载量共同约束下的最优调度决策。通过对现有货物资源分配的驱动策略,生成运输订单货源供求响应的资源调度方案。
0.引言。
针对中欧铁路的运输特点和货源地商品种类的多样性,当前的中欧跨境铁路运输多为大宗的货物,如机械设备、电子产品、批量的食品和药物等,到达目的国后统一进行货物装卸。除此之外,跨境铁路还需商检、通关等过境手续才能保证货物的运输通畅快速。再者,由于轨距差异,使得中欧班列途中需要1-3次换轨增加了整个运输过程的成本[1]。本文针对以上问题,结合各节点城市主要货源和中欧班列运输资源进行调度优化,对中欧班列智能化运输调度问题进行研究。
1.中欧班列开行方案优化模型
1.1 调度模型约束
本文建立模型用有向路线G(V,A)表示中欧铁路运输物理网络,其中V表示所有城市节点的集合,A表示弧的集合。此外,△+(i)表示从节点i出发的弧的集合,△_(i)表示回到节点j的弧的集合,N=V{0,n+1}表示途经节点集合,K表示中欧班列车辆集合。
(1)运输距离计算
目标函数1-1表示最小化班列行驶总距离,故有:

(2)关于节点路径约束
约束1-2—1-4表示班列车辆k在运输路径上的流量限制


(3)关于时间连续性约束
约束1-5表示当前班列k行驶时间的连续性。

(4)列车装载量计算
公式1-6为当前班列k在对所在路线的第一个节点服务结束后的列车装载量的计算公式。

公式1-7为当前班列k在对所在路线的任意一个节点(不包含第一个节点)服务结束后的列车装载量的计算公式。

(5)货流运输路径唯一性约束
根据模型假设货流不可拆分的原则,限制每个运输节点只被分配到一条运输路径,xijk定义为辅助0-1变量,表示区段r和货流(o,d)的实际运输路径的关系,可得以下约束:

2.中欧智能化运输调度策略算法求解
本文模型算法求解主要包含编码与解码、目标函数、种群初始化、聚类、替换、更新、局部搜索和合并这几个操作步骤,求解重点步骤如下:
(1)编码与解码
本文采用的编码方式是将枢纽节点与区域节点同时在编码个体中进行体现。若沿途节点城市数目为N,枢纽节点最多允许K列车进行运输,那么问题中的个体就表示为1~(N+K-1)的随机排列。
(2)目标函数
本节采用给违反约束的运输路线施加惩罚的办法来使解码出的各条运输路线都满足装载量约束和时间窗约束。因此,运输方案总成本的计算公式如下:

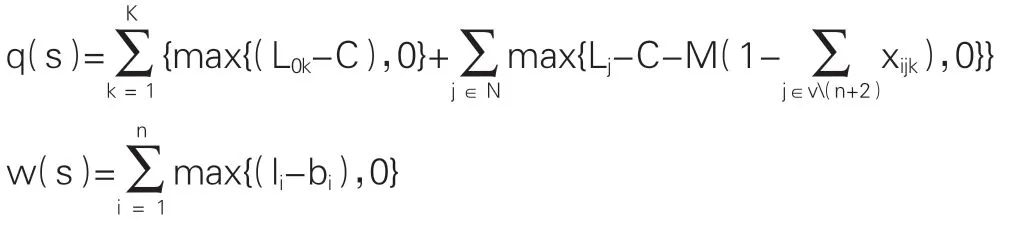
式中,s为个体转换成的运输方案;f(s)为当前运输方案的总成本;c(s)为班列总行驶距离;q(s)为各条运输路线违反的装载量约束之和;w(s)为所有节点违反的时间窗约束之和;α为违反装载量约束的惩罚因子;β为违反时间窗约束的惩罚因子;K为班列车辆集合;V={0,1,2,n,n+1}为所有节点的集合;N=V(n+1)为节点城市集合;l0k为班列k离开枢纽节点的装载量;Lj为班列对节点i服务结束后的剩余装载量;xijk为班列k是否从节点i出发前往节点j;c为班列最大装载量;M为足够大的正数;n为节点城市数目;li为班列到达节点i的时间;bi为顾客i的右时间窗。可根据目标函数公式进一步计算出当前个体的目标函数值。
(3)更新操作
对于本文问题而言,需要结合问题特点,同时引入遗传算法的交叉操作,从而完成个体位置的更新。假设种群数目为NIND,聚类数目为k(k≤2),则更新操作种群中第i个个体的伪代码如下。
如果rang<p_one
1.随机选择1个聚类:
如果rang<p_one_center
a.Xselect1=这个聚类中的聚类中心
否则
b.Xselect1=从这个聚类中随机选出一个个体
对个体Xselect1=进行交换操作后得到新个体Xnew。
否则
2.随机选择2个聚类:
如果rang<p_two_center
a.Xselect1=聚类1中的聚类中心,Xselect2=聚类2中的聚类中心
否则
b.Xselect1=聚类1中随机选出个体1,Xselect2=聚类2中随机选出个体2
对个体Xselect1和Xselect2进行交叉操作后得到新个体Xnew1和Xnew2,选择目标函数值更小的新个体作为此次更新得到的新个体Xnew。
如果新个体Xnew的目标函数值小于第i个个体的目标函数值,则更新个体i=Xnew;否则,不更新个体i。
上述伪代码中涉及了交换操作和交叉操作,交换操作的对象是一个个体,交叉操作的对象是两个个体。
(4)局部搜索操作
局部搜索操作使用破坏算子从当前解中移除若干个节点城市,然后使用修复算子将被移除的节点城市重新插回到破坏的解中。
1.破坏算子
假设节点城市数目为N,要移除的城市数目为L,随机元素为D,则破坏算子的步骤如下。
①从这N个节点城市中随机选择1个城市,如随机选择的城市为,此时被移除的城市集合R=[i],未被移除的城市集合U=[剩余N-1个城市]。
②判断R中城市数目L是否小于等于要移除的城市数目L,如果是,则转至步骤③;如果不是,转至步骤⑤。
③首先,从R中随机选择一个城市r,根据相关性计算公式计算U中所有城市与城市r的相关性;其次按照相关性从大到小的顺序对U中的城市进行排序,排序结果为S;然后根据公式(其中rand∈{0,1},是集合U中节点城市数目,[]表示向上取整)计算下一个被选择移除的城市next。
④将城市next添加到R中,将顾客next从U中删除,转至步骤②。
⑤将R中所有的城市从当前解中全部移除;输出被移除的城市集合R,以及被破坏的解Sdestroy。
2.修复算子
在得到被移除的城市集合R和破坏解Sdestroy的基础上,进行修复算子。假设被移除的城市集合为R,破坏解为Sdestroy,则修复算子的步骤如下。
①初始化修复后的解Srepair,即Srepair=Sdestroy。
②如果R非空,转至步骤③,否则转至步骤⑥。
③计算当前R中的城市数目nr,计算将R中各个城市插回到Srepair的“遗憾值”regret,即regret是nr行1列的矩阵。
④首先找出regret中最大“遗憾值”对应的序号max_index,其次确定出即将被插回的城市rc=R(max_index),最后将rc插回到中Srepair的“插入成本”最小的位置。
⑤更新R(max_index)=[],转至步骤②。
⑥修复结束,输出修复后的解Srepair。
(8)合并操作
合并操作的目的是将Population与offspring进行合并以形成新的Population,但种群数目是一定的,所以需要在Population和offspring中删除部分个体,以保证种群数目依然为NIND。
3.实例分析
将货流数据及相关参数进行计算得到优化前的班列运输总成本,结果整理如下表3-1:

表3-1 优化前班列运输总成本(单位:周)
对西通道中线运输线路利用本文BSO算法优化后的线路运输时间T'和班列开行成本Z'进行计算得到优化后的计算结果表3-2。

表3-2 优化后班列运输总成本(单位:周)
4.结论
与西通道中线当前运行班列的18条线路对比,优化后的调度方案为8条运输线路,班列运输时间优化后减少了76.46%,开行成本优化后减少了47.83%,对中欧班列西通道中线运输系统的效率实现了显著的优化。综合以上分析,根据2020年货流数据及参数指标进行计算,本文设计的调度方案,能够在保证中欧班列在稳定运行的基础上,实现开行成本的降低和运输效率的提高。
引用出处
[1]王春越.基于需求分类的“义乌——汉堡”中欧班列路径优化研究[J].物流商论,2021,05(a):37-39.

