改进风驱动优化算法在水库调度中的应用

顾起豪，张双虎，刘 吟，王 丹，2

（1.中国水利水电科学研究院 水资源所，北京 100038；2.大连理工大学，辽宁 大连 116024）

1 研究背景

水库优化调度特别是发电优化调度是一个多阶段、强约束、非线性的组合优化问题［1］，水库优化调度模型求解方法始终是水库优化调度研究的热点。目前，求解水库调度模型的方法有两种：一种是以线性规划（LP）、动态规划［2-4］（DP）为代表的传统优化方法。该类方法的缺点是效率和精度难以兼顾，容易陷入“维数灾”。因此，专家学者提出了很多降维方法，例如：耦合KL理论与调度特征的降维方法［5］、逐步优化算法（POA）［6］、离散梯度逐步优化算法（DGPOA）［7］、三层并行逐步优化算法［8］、双层动态规划算法（BDSP）［9］等。另一种是基于生物学、物理学和人工智能的具有全局优化性能、稳健性强、通用性强且适于并行处理的现代启发式算法［10］，如改进粒子群算法［11-13］、混沌优化算法［14］、狼群算法［15］、群居蜘蛛优化算法［16］、改进遗传算法［17］等。现代启发式算法鲁棒性强，在一定程度克服了传统算法的求解效率低的缺点。但这些算法以模拟自然界的生物进化或动物运动为主，无明确的物理背景。

风驱动优化算法（Wind Driven Optimization，WDO）是由 Zikri Bayraktar等［18］在 2010年提出的模拟空气运动的一种优化算法。空气中的任何一微小部分可以视为点，简称为“空气质点”。空气质点在外力的作用下，相互影响相互作用，朝着同一方向运行，当气压达到平衡时不再运动，该位置可以理解为最优解。空气运动过程中，每个空气质点位置组合可以认为一个是候选解，空气质点的运动轨迹就是寻优的过程。WDO算法的核心是研究空气质点在大气中的受力运动情况，并结合牛顿第二定律及理想气体状态方程，推导出空气质点在每次迭代中的速度和位置更新方程［19］。算法中的每一项都具有明确完整的物理意义，在实际运用中更加简便、容易理解。近几年，风驱动优化算法已经被广泛应用到电磁优化［20-22］、医学［23］、人工智能［24］、遥感［25］等领域，但尚未在水库优化调度领域中得到运用。

本文对WDO在水库优化调度模型求解中的应用进行了详细的阐述，并提出通过加入扰动策略解决WDO后期收敛速度慢、容易陷入局部最优解的缺陷，通过引入空间压缩机制提高模型求解效率，并将该算法应用到某水库发电优化调度模型求解中。

2 风驱动优化算法

根据牛顿第二运动定律，作用在空气质点上的合力与运动加速度关系如式（1）所示，且加速度和合力的方向始终保持一致。

式中：ρ为空气密度；为加速度；为施加在空气质点i方向上的力。

作用于大气的力包括真实力和视示力。真实力又包括气压梯度力、万有引力和摩擦力；视示力主要是科氏力。科氏力不做功，只改变空气质点运动方向，是地球自转效应的反映。

（1）气压梯度力是空气运动的最基本力，气压梯度力合力可以表示为：

式中：m为空气质点质量；ρ为气体密度；δV为空气质点体积；∇p为气压梯度；“-”表示从高压指向低压运动。

（2）空气质点之间的摩擦力非常复杂，简化如下：

式中：κ为摩擦系数；u为速度矢量；“-”表示摩擦力与运动方向相反。（3）空气质点的重力是垂直与地球表面方向的力，可以表示为：

（4）科里奥氏力是指由于地球自转而使空气质点运行发生偏转的力。科氏力不做功，只改变运动方向，可以表示为：

式中Ω为地球自转的角速度。

根据理想气体状态方程p=ρRT，有

式中：p为气体压强；R为干空气比气体常数；T为理想气体的热力学温度。

令 Δt=1，δV=1，，并把式（2）—式（6）带入式（1），等式两边同时除以ρ，则有：

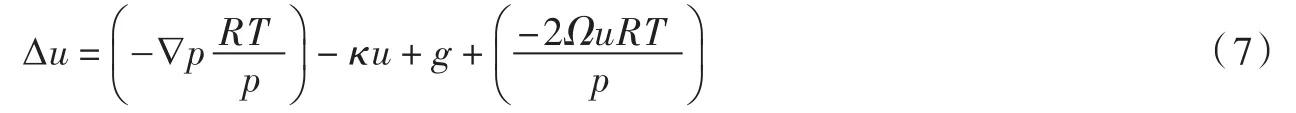
设ut、ut+1分别为空气质点在t、t+1时刻的速度，则Δu=ut+1-ut。根据牛顿第二运动定律的“瞬时性”特点，即加速度和力同时产生、同时变化、同时消失，则式（7）可转化为：

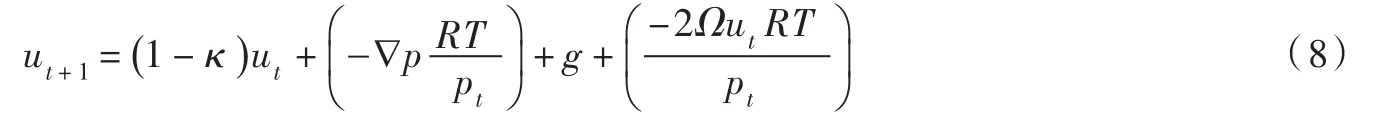
气压梯度力的方向从高压指向低压。定义目前为止空气质点最小压强为popt，即群体当前最优解，与之对应的空气质点位置为xopt。根据气压梯度公式定义，空气质点当前位置与最优位置的气压梯度关系如下：

根据文献［21］，

把式（9）和式（10）带入式（8），则有：

为避免气体压力过大，影响模型稳定性，用压强大小排序来代替实际压力值，popt为1，pt为j；

设RT=α，-2ΩRT=β；科氏力是一种惯性力，为刻画空气质点当前速度受其它维度速度的影响，用近似代替ut，则式（11）可改写为下式：

式（12）是空气质点运动速度更新公式。位置更新公式如下：

3 水库优化调度数学模型

本文建立了兼顾保证出力的发电量最大为目标的水库优化调度模型。即在调度期内根据历史来水过程或预报来水过程，考虑各约束条件，在保证各时段出力不小于电站保证出力的前提下，寻找水库运行调度过程，以达到年发电量最大的目标。具体目标函数如下：

式中：Nt为水电站出力；k为出力系数；Qt为t时段发电流量；Ht为t时段发电水头；T为调度期内时段数；Δt为每个计算时段内的小时数。

主要约束条件包括：

4 应用于水库优化调度WDO算法的改进

4.1 算法设计 WDO算法可以描述为一个由M个空气质点组成的群体在D维空间内运行。速度矩阵U、位置矩阵Z如下：

WDO在水库优化调度模型求解时，空气质点数可以用来描述初始解的个数，空气质点运动空间维数可以用来描述水库优化调度求解时段，速度矩阵U可以用来描述迭代求解过程中水位或库容的变化，位置矩阵Z可以用来描述迭代求解过程中某一状态下的水位或库容。按照一定的随机方法可以生成M个库容变化向量和初始库容向量，。

WDO算法速度更新公式共有4项，其中前3项决定速度更新大小和方向，根据科氏力定义，第4项只改变速度方向、不改变速度大小。WDO算法在求解水库优化调度时，先根据式（12）计算前3项计算速度即时段末的库容变化量，再根据这一库容变化后相邻前后时段是否有弃水，动态调整λ。库容变化更新公式如式（18）所示，时段末水位更新公式如式（19）所示，λ计算公式如式（20）所示：

式中f(·)为根据时段初、时段末库容计算发电弃水函数。

4.2 算法改进 针对风驱动算法求解优化问题存在的易于陷入早熟和搜索效率不高的缺点，本文主要从以下两个方面进行改进。

（1）空间压缩。水库优化调度求解是一个强约束、序贯决策过程，当前的决策不仅影响到当前时段效益，还影响到下一时段效益。在用智能优化算法求解水库优化调度模型时，经常会生成大量的不可行解，导致模型求解效率不高。为此，引入空间压缩策略来提高模型求解效率。空间压缩方法的核心思想是：在求解过程中，根据，考虑各种约束，计算满足约束条件的上下限，并根据下式计算约束更新后的库容：

在进行空间压缩时，采用奇偶相间的方式来更新库容向量，即进行第i+1代库容序列更新时，只对奇数时段末的库容进行更新；进行第i+2代库容序列更新时，只对偶数时段末的库容进行更新，依次来更新提高模型求解效率。水库优化调度求解空间压缩示意图如图1所示。

图1 水库优化调度模型求解空间压缩示意图

（2）扰动。在室内放一个气球，气球在经历一系列运动后会飘在空中静止，此时气球达到平衡状态，处于当前最佳位置。若在气球任一方向上稍微加一点力，气球即会重新开始运动，直到达到新的平衡状态，处于新的最佳位置，这就是扰动的原理。

WDO在求解水库优化调度模型时，若连续多代适应度值变化不大，则可以认为是陷入早熟。对当前最优适应度值对应的库容向量中的任一个时段蓄水状态进行扰动，且随着迭代次数的增加，扰动量要逐渐减少。为此构建以下扰动量计算函数：

式中：ε为扰动量；γ为（0，1）的随机数；θ为常量，经大量试算，θ=4求解效率最高。通过扰动，更新早熟的最优解，使其跳出早熟，继续寻优。

4.3 求解步骤

（1）确定进化代数和群体规模，设置相应参数。

（2）生成初始库容序列（初始解）和速度更新序列。为提高模型求解速度，要保证初始库容序列中有一定比例满足约束条件的解。

（3）开始迭代。按照式（18）—式（21）进行库容变化序列和库容序列的迭代更新，并计算相应的适应度值。

（4）扰动。判断是否陷入早熟，若早熟，对当前最优解进行扰动，进行下一代迭代。

（5）模型终止判断。判断是否满足模型终止条件，满足条件、模型终止；不满足条件，返回第（3）步再次进行迭代。

5 实例计算

为充分验证改进WDO算法的有效性并比较该算法与标准WDO算法及PSO算法的性能差异［26］，以某水库优化调度模型求解为实例进行验证。该水库是以发电为主，兼有防洪任务的年调节水库。水库的正常蓄水位630 m，相应库容为55.63亿m3；死水位590 m，相应库容为26.62 m3；6—7月份汛限水位为626.24 m，8月份汛限水位为628.12 m；电站装机容量为3000 MW，电站保证出力600 MW；水电站综合出力系数8.5。为了避免或尽可能减少社会用水挤占河道生态用水产生的不利影响［27］，该水库中最小生态下泄流量设置为300 m3/s。为兼顾保证出力的发电量最大为目标进行优化调度计算，计算时段为月。

5.1 合理性分析 表1为引入改进策略的风驱动算法（IWDO）求解水库优化调度模型计算结果。由表1可知：6、7月份水位不高于汛限水位626.24 m，8月份水位不高于汛限水位628.12 m，其余月份水位均高于死水位590 m，低于正常蓄水位630 m；各月平均下泄流量均大于最小生态下泄流量300 m3/s；电站出力均大于保证出力600 MW。计算结果表明，IWDO求解水库发电优化调度模型是可行的。

表1 IWDO运算结果

5.2 改进策略效率分析 为了分析本文提出的空间压缩和扰动策略在模型求解的作用，进行了三种情景对比。一是标准风驱动算法WDO；二是增加了空间压缩策略的风驱动算法；三是增加了空间压缩和扰动策略的风驱动算法IWDO。三种算法求解水库优化调度，适应度值随迭代次数的变化过程如图2所示。从图2可以看出，标准风驱动在第62代开始就陷入了早熟，此后迭代几十次内适应度值变化很小，适应度值为97.93亿kW·h；加入空间压缩策略后在第29代达到最大适应度值98.53亿kW·h；再加入扰动策略，从第29代之后，适应度在持续缓慢的增加，到100代时适应度值达到98.88亿kW·h，到200代时适应度时达到99.01亿kW·h，到500代结束迭代时，适应度值达到最大99.25亿kW·h。上述分析结果表明，在标准风驱动中加入空间压缩策略可以明显提高迭代效率；加入扰动策略后，能持续缓慢地提高适应度值。

图2 改进策略效率分析

5.3 IWDO算法搜索性能分析 为了进一步分析IWDO算法在求解水库优化调度模型时的性能，本文又应用了粒子群算法（PSO）进行优化求解，目标函数与约束条件均不变。两种算法适应度值对比如图3所示。从图3可以看出，IWDO和PSO两种方法求解水库优化调度，最终适应度值相差不大，但是IWDO效率更高。IWDO第30代适应度值就与PSO第195代适应度值相当。上述分析结果表明，IWDO求解水库优化调度，效率更高。

图3 IWDO搜索性能分析

6 结论

本文以风驱动算法为基础，提出了改进的风驱动算法IWDO，并将其应用到水库优化调度模型求解中，通过实例研究可得：

（1）标准风驱动算法仍然存在着早熟和收敛速度慢的问题。经过实例计算，标准风驱动优化算法在第62代陷入早熟，且最终适应度值为97.93亿kW·h。在对其改进的过程中，当仅加入空间压缩策略时，在第29代就达到最大适应度值，为98.53亿kW·h；若再加入扰动策略，适应度值随着迭代次数的增加，不断上升，最终达到99.25亿kW·h。由此可见，本次研究提出的空间压缩策略可明显提高风驱动算法求解水库优化调度的效率，提出的扰动策略能有效避免算法“早熟”，两种策略同时具有显著提高风驱动算法求解水库优化调度的性能。

（2）改进的风驱动算法在迭代30次得到的适应度值与粒子群算法迭代195次得到的适应度值相当；优化后的风驱动算法迭代200次适应度值为99.02亿kW·h，比PSO算法迭代相同代数适应度值增加0.1亿kW·h；优化后的风驱动算法最终求解适应度值为99.25亿kW·h，比PSO算法增加0.33亿kW·h。

（3）空间压缩策略还可以应用到其它智能算法中，提高算法求解效率。

因此，改进的风驱动优化算法（IWDO）为解决水库优化调度模型的有效算法。