基于非对称贴近度的水库移民后期扶持效果评价模型研究

郑凯鑫，许桂生

（华北电力大学 水利与水电工程学院，北京 102206）

1 研究背景

国家对大中型水库移民实行前期补偿加后期扶持的政策，后期扶持工作是帮助移民重建社会和经济关系的系统工程［1］。为了能够合理评价水库移民后期扶持政策的实施效果，国内学者对此做了许多研究工作。水库移民后期扶持效果评价大致分为三步：建立指标体系、计算各指标权重、建立综合评价模型。指标体系的构建大部分以水库移民安置方案、监测评估报告和实地调研情况为依据。计算指标权重有主观赋权法和客观赋权法。主观赋权法常用德尔菲法和层次分析法等利用专家或个人的知识及经验，对权重做出判断。客观赋权法根据原始数据之间的关系通过一定的数学方法来确定权重，其判断结果不依赖于人的主观判断，有较强的数学理论依据。常用的客观赋权法通常包括主成分分析法、离差及均方差法、多目标规划法等。在综合评价模型研究中，牟立［2］基于主成分分析的模糊综合评价法对贵州省三县（市）水库移民后期扶持效果进行了评价。王洁琼［3］运用层次集对分析法，基于白化权函数的灰色聚类法对河南省两个县区的水库移民生产生活水平进行了评价。徐鑫等［4］利用主成分分析法与人工神经网络对北京市各个区县水库移民政策实施效果进行研究。张爽［5］运用层级分析法和专家打分法对河南省南水北调中线工程进行了移民村社会治理绩效评价研究。王美［6］基于层次分析法、熵权法和集对分析法模型对陕西省的5个县（区）进行了后期扶持政策实施评估的实例分析。吴杨［7］基于可拓关联函数对陕西省县区水库移民后期扶持政策实施情况进行了评价。赵敏等［8］采用数据包络分析法对水库移民安置进行了评价。在采用模糊综合评判法对后期扶持政策的实施效果评价时，多采用最大隶属度原则。但该方法容易丢失大量的信息，可能会导致评价结果不合理。为弥补最大隶属度原则的缺陷，张晓平［9］提出了非对称贴近度理论。吴菊华等［10］基于非对称贴近度建立了地质灾害危险性评价模型。王瑞峰等［11］以模糊熵和非对称贴近度相结合建立了机床安全预警模型。本文首先结合文献和专家意见建立后期扶持效果评价指标体系，利用层次分析法确定指标权重，在此基础上构建了基于非对称贴近度的移民后期扶持效果评价模型，并将其应用于广东省龙门县大中型水库移民后期扶持政策实施效果评价。

2 水库移民后期扶持效果评价指标体系

水库移民后期扶持是一项复杂的社会系统工程，涉及面广，本文以发改农经〔2011〕1033号文件［12］为依据，结合现有文献［4，13-14］和专家意见，构建了目标层、准则层和指标层，其中准则层包括收入结构、生产条件、生活条件、基础设施、社会保障五个层面，指标层包括人均可支配收入、耕地面积、新农合比例、医疗情况等16个指标。具体见表1。

表1 水库移民后期扶持效果评价指标体系

3 基于非对称贴近度的模糊综合评判模型

模糊综合评判法中最常用的方法是最大隶属原则，由于最大隶属度原则只考虑模糊子集中最贴近的集合，容易漏失信息，可能会导致评估结果失真［15］。为弥补最大隶属度原则的缺陷，张晓平［9］提出了非对称贴近度理论。本文在此基础上建立了水库移民后期扶持效果评价的模糊综合评判模型。

3.1 确定指标集 设定准则层Z=(Z1，Z2…，Zm)为目标评价的所有准则集合，各准则之间相互独立互不影响，即Zi∩Zj=0(i≠j)；准则层由多项指标层构成，指标层集合可表示为Zi=(Zi1，Zi2，Zi3，…，Zin)(i=1，2，…，m)，Zi为准则层集合，Zin为指标层集合，基于此设定，建立水库移民后期扶持效果评价指标集合，如表1所示。

3.2 确定评价集 水库移民后期扶持政策实施效果评估属于复杂系统问题，涉及指标较多，若评价等级划分过少，可能会导致信息缺失；划分过多，各等级所属区间范围可能过小，不利于操作。本文通过咨询专家意见和查阅文献资料，将目标层，准则层和指标层三层指标划分为四个等级：｛优v1，良v2，中v3，差v3｝，即

3.3 计算隶属度评价矩阵 水库移民后期扶持效果评价的隶属度，表示的是各个指标对最终结果的支持程度，通过将各指标对各等级支持程度量化来构建隶属度矩阵，取值为（0，1）的实数。隶属度模糊评价矩阵的表达式为：

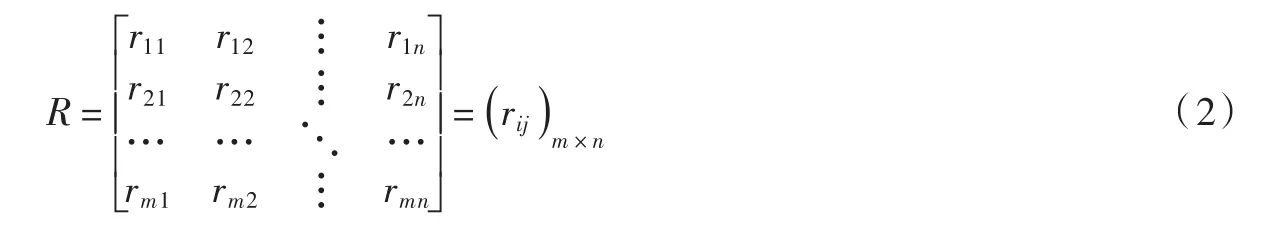
式中rij为指标i的j级隶属度值。

根据评价结果构造的模糊评价矩阵，本文采用平均加权的方式计算各准则层对各级评语的隶属度：

式中Bm为准则层指标隶属于评价等级vi(i=1，2，…，j)的程度。

3.4 确定指标权重 第一步：本文采用1～9标度法，以Saaty教授提出的1～9标度法作为专家打分的依据［14，16］邀请专家打分，对层次结构中的每一层指标相对于上一层的指标的重要性进行两两比较，构造出判断矩阵。

第二步：构造出判断矩阵后，求出该矩阵的特征值和特征向量，求出最大特征值λ_max并将特征向量进行归一化，用W表示归一化后的特征向量。

第三步：判断矩阵偏离一致性指标检验。若不符合，则需要对判断矩阵进行修正。若通过一致性检验，将求得的特征向量归一化即为各个指标的特征向量W。

3.5 基于非对称贴近度进行综合评价

（1）确定评判结果向量。确定权重向量W和隶属度矩阵R后，为防止有效信息丢失，本文采用加权平均算子对指标隶属于各评价等级的程度进行处理。

设评判向量B=(B1，B2，…，Bm)，则有：

式中Bm为准则层指标隶属于评价等级vi(i=1，2，…，j)的程度。

（2）计算非对称贴近度。贴近度是对两个模糊子集的一种度量，在对评判结果的计划中最常用的方法是最大隶属原则，但该方法在某些情况下是失效的，会缺失部分信息。为此文献［9］构造了非对称贴近度来进行等级评判，并验证了该方法的有效性。非对称贴近度的定义如下［9］：

式中：μA、μB分别为模糊集合A、B的隶属度；vk为对应的k级评语；p为调节因子，为了使评价结果向更好的方向集化，本文取p=1。

若水库移民后期扶持效果评价等级分类V={v1，v2，…，vj}，则称Di=(0，…，1，…，0)=(d1，…，di-1，1，di+1，…，dj（)1为第i个分量）是vi的特征模糊子集。则其非对称贴近度可按如下方法［17-18］计算：

Step1：对B进行标准化。首先把bi排在第一位，对任意i1、i2∈ic，若|i1-i|≤|i2-i|，则把bi1放在bi2的前面。标准化后的B记作B(i)=(b1i，b2i，…，bji)=(bi，bi-1，bi+1，bi-2，bi+2，… )。相应地，对Di进行标准化，得D1=(d11，d21，…，dj1)。

Step2：计算非对称贴近度N(B，Di)：

式中：p=1。

4 实例分析

本文基于广东省2019年度大中型水库移民后期扶持监测评估数据，对惠州市龙门县水库移民后期扶持政策实施效果情况进行评价，邀请20位水库移民专家，根据龙门县当地后扶政策实施情况结合专家个人的判断，对指标层16个指标进行效果评价，并将结果汇总统计，如表2所示。

表2 指标层专家评价结果统计

（1）根据专家评判结果，构造出的评判矩阵如下：

（2）权重计算。采用3.4所述的1～9标度法对准则层5个指标构造判断矩阵

通过编程计算，求得最大特征值λmax=5.0492，，RI=1.12，，通过一致性检验。得到准则层权重向量为：

同理可计算出指标层权重向量：

（3）利用式（4）求得B1，B2，B3，B4，B5，进而得到评价矩阵

（4）评判结果向量

根据权重向量W及评价矩阵R，由式B=WR得评判结果向量为：

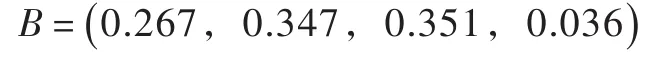
（5）非对称贴近度评判

对B进行标准化：

由式（6）和式（7）计算非对称贴近度N(B，Di)(i=1，2，3，4 )，可知

因此计算的非对称贴近度为

（6）结果分析。由评判结果向量B可知，龙门县水库移民后期扶持政策实施效果对优、良、中、差的隶属度分别为：0.267、0.347、0.351、0.036。根据最大隶属度原则Bmax=0.351，所对应的评价等级为“中”，但由非对称贴近度结果可知，所属评价等级应为“良”。

作者在2019年度广东省大中型水库移民后期扶持政策实施情况监测评估项目的实地调查中，了解到龙门县移民的生活水平较好，后扶项目的实施从根本上改善了移民的生产生活条件，提高了移民的生活水平。其中移民的收入来源依靠二三产业较多，龙门县移民管理部门在对移民的帮扶工作中，与当地政府与企业积极合作，共同发展特色产业，带动移民发展经济，开创了一条致富道路，移民对现状生活较为满意。龙门县对移民后期扶持政策的实施是有效的，后期扶持政策的实施进一步加快了移民生产生活水平的提高，移民生产生活水平越来越好。因此从实地调查情况来看，评价结论为“良”比“中”更合理。

事实上，根据隶属度的计算结果，“良”和“中”的隶属度非常接近，而“优”和“良”的隶属度之和明显大于“中”的隶属度，且明显大于“中”和“差”的隶属度之和。若按最大隶属度原则判定为“中”，显然不妥。最大隶属度原则没有综合利用评判结果向量的信息，导致最终评价结果“失真”，而非对称贴近度能够将各专家的评价结果更好地集化，更准确地反映评价对象与评价集之间的贴近程度。因此相对于基于最大隶属度原则的模糊综合评判法，基于非对称贴近度的后期扶持效果评价模型给出的评判结果“良”更为合理。

5 结论

（1）本文结合现有文献和专家意见建立水库移民后期扶持效果评价指标体系，利用层次分析法确定指标权重，在此基础上构建了基于非对称贴近度的移民后期扶持效果评价模型，并将其应用于广东省龙门县大中型水库移民后期扶持政策实施效果评价，可为水库移民后期扶持工作实践提供参考。

（2）通过文献分析和实际应用表明，对于移民政策中的后期扶持效果评价，目前多采用基于最大隶属度原则的模糊综合评判法，该方法没有综合利用评判结果向量中非最大分量的信息，可能会导致评价结果“失真”。

（3）本文构建的基于非对称贴近度的移民后期扶持效果评价模型有效地克服了最大隶属度原则的上述缺陷，能够将各专家的评价结果更好地集化，更准确地反映评价对象与评价集之间的贴近程度，确保评价结果符合客观实际。实例分析表明，本文模型与基于最大隶属度原则的模糊综合评判法相比，给出的评价结果更为可信、合理。