汊道平面形态对河口潮波传播的影响

冯浩川，王崇浩，郭传胜，王玉海，张 蔚

（1.中国水利水电科学研究院 流域水循环模拟与调控国家重点实验室，北京 100048；2.河海大学 水文水资源与水利工程科学国家重点实验室，江苏 南京 210098）

1 研究背景

在潮汐河口，水位过程可以比较直接地反映潮波运动的影响。此外，水位过程由于受到径流和潮波两种动力的影响，会兼具潮波运动的周期性变化以及径流动力在长周期内相对稳定的两种特点（非稳态特征）［1］。径流与潮汐相互作用所导致的一个关键现象是水位的波动以及流速的往复，这两者的变化在感潮河段呈现出完整包含大、中、小潮的半月潮（大小潮）周期性特征［2-3］。径潮相互作用会使得潮区界以下区域内全日潮周期平均的水位分布梯度相对恒定［4-5］，长周期平均的水位梯度与低频水位变化的影响范围相较于全日潮、半日潮等规则潮汐动力的影响更为深入内陆［5-6］。这一现象往往反映了潮波波长大幅度增加的结果，也正因为如此，潮波通过河流向陆地传播的范围超越了规则天文潮所能达到的上限［7］。同时，半月潮（大小潮）的存在也大大影响了感潮河段在这一周期内的水位变化，潮波运动通过与径流的相互作用对河口汊道乃至上游较大范围河段内的水位分布状态产生着重要的决定作用。与此同时，潮波运动在复杂地形条件的影响下，也会因为本身的传播特征而对动力状态的分布产生明显的调整作用［8-9］，使得水动力状态演变出新的复杂的时空分布特征。

受潮波动力影响明显的河口发育过程往往伴随着河道分汊现象的产生［10-11］，即出现了通常意义上的河口分汊汊道。在有分汊现象的潮汐河口，径流与潮汐相互作用本质上是径流与潮汐动力通过相互调节在分汊河道乃至河网系统中的重新分配，这一分配格局必然对泥沙输运、河道海岸演变以及盐水入侵等河口物理过程产生不可忽视的影响［12-15］。同时，作为内陆与外海、径流和潮汐两种动力相互影响的区域，由深海传播而来的潮波简谐振动在这一区域由于受到复杂地形和上游径流的阻滞、调节作用，其动力状态往往表现出极强的非线性［1］。此外，由于潮波运动时间以及空间上的往复性，径流与潮汐相互作用过程在分汊节点处的不均匀分配与汇聚收敛之间存在周期性的交替转化，更加剧了这一区域动力过程的复杂性。因此，开展汊道平面形态对河口潮波传播的影响研究具有重要的科学意义。

2 河口模型

本文以河口分汊汊道为原型，建立理想模型，探讨分汊河口中汊道平面形态对潮波运动的影响。这类河口汊道在平面形态上最为突出的几个特点是，河道弯曲转折，从口门向上游方向河道宽度收敛。根据这些特征，利用Delft3D建立一组河口分汊理想模型［16］，从而对比分析这些因素对潮波传播的影响。为了突出这三个特点的作用而尽量忽略其他因素的影响，各个模型平面形态采用概化设置，模型1、2、3、4的平面形态以及网格设置如图1所示。

图1 河口模型网格示意

本文建立的几组理想模型（包含河口汊道）自上而下总长度均设置为600 km，且主干河道全部在距离上游边界500 km处分为南北两个汊道，南侧主汊道沿干流方向继续向下游直线延伸100 km至河口（下游边界）。模型北侧支汊在分汊口处与主干河道以及南侧主汊道垂直分汊，并同时以不同弯曲形态向下游延伸100 km至河口。为了消除两条汊道长度不同而对潮波传播产生的影响，模型中南支以及北支汊道的长度均设置为100 km。主干河道（0～500 km范围）宽度由上游边界处的2 km向下游逐步展宽，到达分汊口处（长度500 km处）展宽至8 km。模型以从上游向下游为正方向，即以向海侧为正。

模型1、2、3中，北支的平面形态分别代表直线（汊道不弯曲），四分之一圆弧弯曲（整个汊道平面形态为四分之一圆弧）以及垂直弯曲（汊道从上游自下游1/3处存在半径为5 km的四分之一圆弧）三种状态，这三个模型模拟的结果将用来重点探讨北支汊道不同的平面弯曲形态对潮波传播的影响。这三个模型中的南支汊道全程宽度保持为8 km，北支汊道全程宽度则固定为2 km，南北两个分支汊道的宽度均保持沿程不变。分汊汊道宽度保持恒定是为了消除汊道宽度收敛的影响。

上述所有模型主干河道部分以及模型4的南北两侧支汊宽度均按级数展宽，其级数展宽公式如下：

式中LW为级数延展长度系数，s为沿程距离，由于主干河道以及模型4的南北支延展程度不同，所以延展长度系数不尽相同，具体参数详见表1。

为了突出河口汊道平面形态的影响，模型1、2、3、4采用相同的沿程水深设定。具体来说，由模型上游边界处（0 km处）水深2 m均匀线性过渡至分汊口处（沿程500 km处）的8 m，同时分别在南北支汊道上游部分（沿程距离500～505 km）范围内向下线性加深至10 m，南北支汊道下游（沿程距离505～600 km）范围内剩余的95 km汊道水深恒定为10 m［17］。据此分别对模型1、2、3、4进行模拟，模拟时长设定为30 d，时间长度包括初始计算所需的收敛时间以及结果分析所需的一个大小潮周期（约15 d），下游边界采用M2分潮与S2分潮叠加的潮位过程驱动模型动力过程，这两个分潮相互叠加、干涉可以产生倍潮以及复合分潮。模型具体参数设定见表1。

为了确认模型网格划分对模拟精度的影响，本研究对网格设置进行敏感性测试。模型初始设定在上游干流及南侧支汊宽度上设定32个网格，北支宽度上设定8个网格。此外，提高模型网格精度，与模型初始网格设定进行对比。具体地，将模型网格在河道宽度方向上加密一倍，即上游干流及南侧支汊在宽度上网格个数设定为64，而在北支宽度上设定为16个网格。分别对这两组模型进行模拟，通过对比模拟水位及流速发现，模型在网格加密前后的结果高度一致，这说明最初的模型网格设定可以精确的反映计算区域的水动力特征，模型满足研究的精度要求。

3 计算结果

3.1 主要分潮簇对水位分布的贡献度 潮波动力在受到径流影响的条件下，其传播过程中会产生明显潮波变形，但也使得水位过程产生出明显的周期性特征。潮波对水位过程的周期特性影响可以细分为，四分之一日潮周期（D4）、半日潮周期（D2）、全日潮周期（D1）以及半月潮周期（D1/14）。径潮共同作用下水位过程会在这四种分潮簇的叠加作用下呈现出周期性的涨落特征。因此，各个不同周期之间的水位分布状态可以细致地反映径潮动力在特定平面形态条件下的作用状态，也能够体现出潮波运动过程中不同分潮簇对水位分布的贡献程度［18］，方法如下：

式中，η为原始潮位序列η1，η2以及η4分别为全日潮周期（D1）、半日潮周期（D2）、四分之一日潮周期（D4）分潮簇对水位的贡献度，而η0是全日潮周期平均潮位。ω为全日潮周期频率，因此2ω、4ω以及ω/14分别为半日潮、四分之一日潮和半月潮周期频率。φ1、φ2、φ4和φ5则分别代表全日周期（D1）、半日周期（D2）、四分之一日周期（D4）和半月周期（D1/14）分潮簇的初始相位。

为了比较径流潮波动力在理想模型1、2、3、4内的差异，需要针对这四个模型的潮位模拟结果进行小波分解，通过卷积及反卷积运算［19］，分离出上述主要分潮簇对水位分布的贡献度，以确定径流潮汐过程对水位变化产生影响。根据上述方法，将潮波的作用主要分为四分之一日潮（D4）、半日潮（D2）、全日潮（D1）以及大小潮（半月潮，D1/14）周期作用下的波动变化，即分别得出这四组分潮簇对水位分布的贡献度，结果如图2、3、4、5中（a）所示。同时，也对模型一个大小潮（半月潮周期）的水位过程进行平均，得到了大小潮平均水位η的分布状态，结果如图2、3、4、5中（b）所示。由于理想模型1、2以及3的结果导出的各个周期分潮簇对水位分布的贡献度十分接近，因此，模型1/2/3的结果在图2与图3中合并展示。

图2 模型1、2、3主要分潮簇对水位贡献度的分布状态

图3 模型1、2、3河口分汊区主要分潮簇对水位贡献度的分布状态

图4 模型4主要分潮簇对水位贡献度的分布状态

图5 模型4河口区主要分潮簇对水位贡献度的分布状态

从图2与图4中可以看出模型1、2、3、4中主要分潮簇对水位贡献度在上游河段（0～500 km部分）的分布状态，其中四分之一日分潮簇（D4）对水位贡献在河道的分布状态从河口向上游出现先增加后减小的态势，半日分潮簇（D2）对水位贡献在河道的分布状态则呈现出递减态势；四分之一日分潮簇和半日分潮簇对水位的贡献在上游河道逐步趋近为零。全日分潮簇（D1）对水位贡献在河道的分布状态呈现出沿上游方向先减小后增加再减小的态势，而半月分潮簇（D1/14）对水位贡献在河道的分布状态呈现出沿上游方向增加后减小的态势。

由图2与图3可知，模型1、2、3南支与北支汊道的主要分潮簇对水位贡献度的沿程分布状态完全一致，即可认为，水位分布在南支与北支的变化仅与其到口门（下游边界）的距离有关，这说明支汊道（北支）的平面形态在较大范围尺度上的弯曲转折，对原有径潮动力过程的影响是比较小的。

此外，为了对比各个周期分潮簇对水位贡献度分布与大小潮平均水位分布的相似程度，本文首先对各个周期分潮簇对水位贡献度分布与大小潮平均水位分布除以各自沿程距离500 km至600 km中的最大值，即进行归一化处理。而后对比分析归一化结果之间的Pearson相关系数，发现半月潮（D1/14）周期分潮簇对水位贡献度分布与大小潮平均水位分布的归一化相关系数在模型1、2、3中均为南支0.9942及北支0.9942，在模型4中为南支0.9925，北支0.9946，体现了高度的相似性（见图3（b）、图5（b））。由于半月周期潮簇通常是潮波在河口汊道与径流动力相互作用引起的，因此水位分布的高度相似性证明了径潮相互作用对潮汐汊道水位分布的决定性影响。

模型4的河口分汊区水位分布与前三个模型有较为明显的不同，此外分潮簇对水位分布的贡献度在模型4中也与模型1、2、3不同。具体体现在：模型4中南北支汊道大小潮平均水位较低，同时，模型4中南北两侧汊道中半日周期潮簇（D2）的振幅均大于前三个模型。模型4中不同的水位分布结果是由汊道内更强的潮动力所导致的。由于潮波在任何河口汊道中的传播都可以看作是入射波和反射波的叠加，因此在某些特定汊道内会不可避免地产生共振效应。当河口汊道中存在宽度收敛时，会趋于使共振效应发生在较长的汊道中，从而对振幅有增幅效应。因此，由于南北支汊道在模型4中不同程度的宽度收敛，同时汊道长度较长（总长约100 km），因此潮波在这两条汊道中传播得到一定程度的加强而使得其振幅衰减相对较慢。

理想分汊河口的潮位分布特征以及半月潮周期分潮簇对水位贡献度的分布状态与马哈卡姆河口［18］相关研究成果相一致，即马哈卡姆河口潮平均水位分布状态与半月潮周期分潮簇对水位贡献度较为接近，印证了理想模型中半月潮（D1/14）周期分潮簇对水位贡献度分布与大小潮平均水位分布最为相似的结论。马哈卡姆河口位于印尼加里曼丹岛东侧海岸，河口分汊众多且大致呈对称的平面分布［18］。这进一步说明本文关于理想模型水位分布的研究成果有明显的实际意义。马哈卡姆河口水位分布状态以及半月潮周期分潮簇对水位贡献度如图6所示。

图6 马哈卡姆河口潮位分布特征及半月潮周期分潮簇对水位贡献度的分布状态示意图［18］

3.2 动量平衡分解 为了研究不同平面状态下河口汊道径潮动力过程的影响，本文根据各项因素对径潮动力的影响过程，将流体连续性方程带入动量方程，经过潮周期积分后平均，分解动量平衡过程，将动量的潮周期平均项分解为压力梯度项、对流扩散以及摩阻项［20］，具体过程如下所述：

式中：Q代表断面流量，t代表时间，U代表断面过流流速，A代表断面面积，η代表断面水位，上述各项在潮周期内随时间变化而变化；Am代表断面潮周期平均面积，s代表断面沿程距离，H代表断面平均水深，Z代表断面平均底高程。W代表断面平均宽度，这几项在潮周期内为固定值。Ttemp代表动量的潮周期平均项，Tadv、Tpres以及Tfric分别代表了对流项、压力梯度项以及摩阻项。这一形式的方程可以将动量过程分解为压力梯度、水平输运以及底床摩阻效应的影响，用以分析这几项作用在潮周期内的相互平衡过程。

此外，前述研究发现河口汊道不同的弯曲形态对潮波传播的影响微乎其微，即模型1、2、3中的潮波传播过程基本接近。因此在涉及动量平衡的研究中，本文只针对模型3、4开展，突出探讨汊道宽度收敛效应对潮波传播的影响。具体来说，本文分别在模型3以及模型4北侧支汊选取断面1、2、3，利用公式3的方法计算各个断面动量平衡状态。为了便于直接对比两个模型动量平衡状态的差异，三个断面在模型3和模型4中的相对位置一致，位置如图7所示。

图7 动量平衡分解断面位置示意

模型3与模型4中各个断面动量平衡分解状态如图8所示，图8（a）、图8（b）、图8（c）分别代表模型3中断面1、2、3的结果；图8（d）、图8（e）、图8（f）则依次代表模型4中断面1、2、3的结果，两个模型中对应断面的形状均保持一致。从两个模型的动量平衡分解结果中可以看出，在模型的北支汊道径潮动力主要体现为压力梯度项与摩阻项相平衡，水平输运项量级相对较小。压力梯度项主要反映水位变化引起的压应力变化，而摩阻项主要体现了水体运动过程中的能量损耗情况。此外，模型3的三个断面上动量分解的压力梯度项及摩阻项绝对值均小于模型4中对应断面的结果，模型4三个断面上动量分解各项相对于模型3的绝对值变化幅度见表2，其中水平输运项量级相对较小，因此其变化参考意义不大。这说明汊道宽度收敛在一定程度上增强了潮波动力的传播，同时也证实了模型4中北支汊道潮平均整体偏低的原因是由于潮波动力相较于其他模型更强。

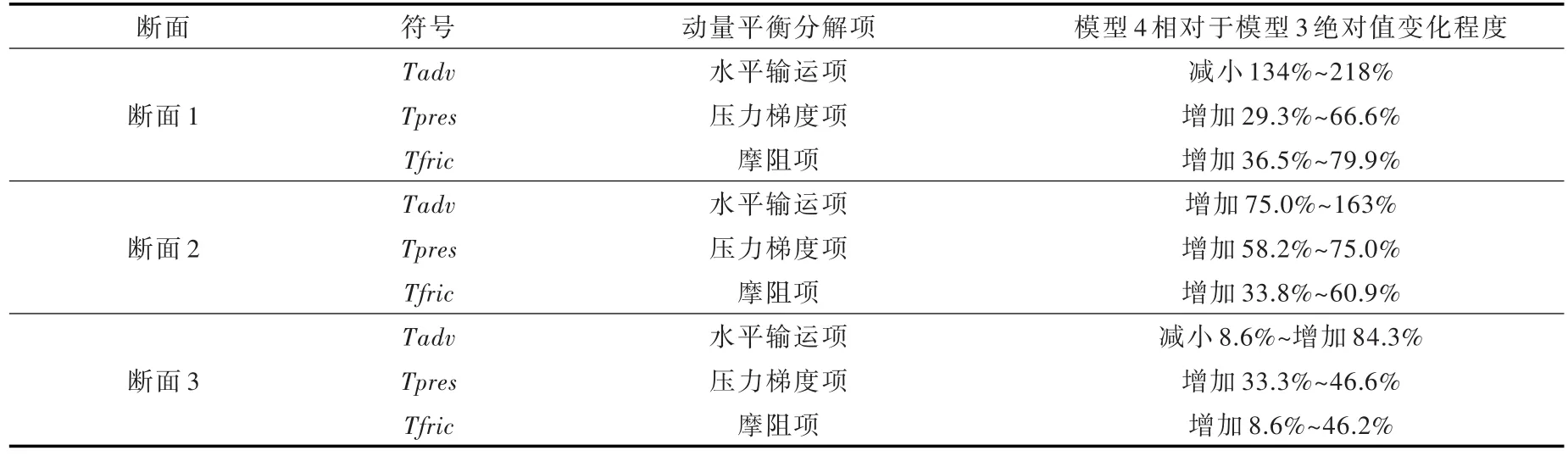
表2 模型3与模型4各断面动量平衡分解项变化

图8 模型3与模型4各断面动量平衡分解状态

4 结论

河口汊道潮平均水位分布受汊道弯曲形态影响较小，而宽度收敛的存在使得汊道内潮平均水位一定程度上整体降低。说明在河口汊道平面形态特征中，汊道单纯的弯曲形态对潮波传播影响较弱，而汊道的宽度收敛效应能够对潮波传播产生较为明显的影响。

潮波运动在河口汊道通过与径流相互作用而对水位过程产生较为明显的影响，半月潮周期分潮簇对水位变化的贡献度与河口大小潮平均水位分布形态接近，说明潮波动力通过与径流的径潮相互作用产生的长周期属性能够对河口水位分布产生较强的决定作用。

汊道宽度收敛的平面形态促使潮波传播出现辐聚效应，增强了潮波传播。具体而言，汊道宽度收敛主要促使动量平衡中的压力梯度项及摩阻项增强，促进了潮波向河口上游的传播过程。河口汊道平面形态通过对动量平衡过程的调整而对潮波传播产生影响。