基于絮凝动力学的泥沙絮凝沉降规律研究

马 林，张 根 广，孟 若 霖，余 远 浩，张 锡 民

(西北农林科技大学 水利与建筑工程学院，陕西 杨凌 712100)

0 引 言

在自然界中，黏性细颗粒泥沙由于其比表面积大，颗粒之间相互作用加强，重力对颗粒的作用相对减弱，致使黏性细颗粒泥沙很少以单颗粒形式存在，而是以集合体形式出现，这种现象称为“絮凝”[1]。泥沙絮凝现象影响着泥沙运动，包括泥沙沉积和输运运动等[2]，并对河口海岸地理和周边环境等有着重要影响。絮凝发生一般需要满足2个前提条件[3]：① 泥沙颗粒间的相互碰撞；② 碰撞后泥沙颗粒粘结在一起。研究发现，影响泥沙颗粒间相互碰撞、絮凝的原因主要有：① 因布朗运动导致颗粒间碰撞发生絮凝；② 沉速大的颗粒在沉降过程中碰撞沉速小的颗粒，导致差速沉降絮凝；③ 湍流运动使颗粒碰撞而发生絮凝[4]。泥沙絮凝问题一直是众多学者研究的热点。如Winterwerp等[4]试图建立絮凝沉降模型，利用数学公式来描述絮凝体沉降变化过程；Maggi等[5]通过将分形维度计入絮体横截面积，显著改善了絮体沉速模型；McCave[6]研究了静水条件下布朗运动对絮凝的影响，发现布朗运动对泥沙絮凝有着重要的控制作用；Krishnappan[7]通过求解不同组分的平衡方程，在泥沙输送模型中考虑了布朗运动的影响，很大程度上改善了模型的精准度；Son等[8]认为絮体在破碎过程中絮体的屈服强度与破裂面的净固体面积成正比，因此建立了一个含有可变分形维数和可变屈服强度的絮凝模型，并将其引入絮凝体尺寸预测。Stolzenbach等[9]研究发现：在颗粒尺寸相差较大的情况下，由差速沉降引起的絮凝效果是显著的。

Allan等[10]基于胶体化学及DLVO理论认为，泥沙颗粒间能否发生絮凝取决于泥沙颗粒间的相互引力与斥力，当引力起主导作用时，泥沙颗粒朝着絮凝方向发展，反之则向着絮凝解体方向发展。关许为等[11]在比较一、二级动力学模式后认为：二者都可用于絮凝速率系数和平均沉降速度问题的研究，但二级动力学模式用于数据拟合的相关性更好。陈洪松等[12]通过分析Nacl对静水絮凝动力学模式的影响发现，加入拟合参数的动力学模式拟合效果更好。但关许为[11]和陈洪松[12]均没有从理论方面给出絮凝过程与电解质浓度、泥沙含沙量等因素之间的关系，且无法合理解释某一影响因素发生变化时絮凝过程将发生如何变化。因此，本文拟以絮凝动力学为基础，建立静水条件下的絮凝动力学方程及絮凝速率系数表达式，据此推导不同含沙量和电解质浓度条件下浑水体系中絮凝过程的半衰期，可用于求解絮凝平均沉降速率等有关参数。

1 胶体稳定理论—DLVO理论

在20世纪40年代，基于扩散层模型，Derjaguin，Landau，Verwey和Overbeek分别提出溶胶稳定性理论，即DLVO理论[13]。DLVO理论[13]认为，胶体的稳定性取决于粒子间的相互吸引力和斥力，若引力大于斥力，则为稳定，反之则不稳定。在泥沙絮凝沉降研究方面，DLVO理论得到了学者的广泛认可和应用[14-16]。

胶粒间的引力本质上就是范德华引力，因此Hamaker假设：胶体间引力等于分子之间相互作用力之和。对于大小相同的两个球形粒子，其引能VA[13]表达式为

(1)

式中：H为Hamaker常数，是物质的特征常数，与物质的性质有关，其数量级为10-20J；rm为颗粒表面的间距，m；d为泥沙单颗粒粒径，m。

由双电层模型理论可知：当颗粒相互靠近时，因范德华引力作用，颗粒表面的双电层将发生重叠，由此改变了表面电荷分布，使颗粒间产生斥力。对于球形粒子，粒子间斥能VR[13]表达式为

(2)

式中：κ-1一般认为双电层厚度，μm；K为波尔兹常数，1.380 650 5×10-23J/K；n0为离子浓度，表示单位立方厘米中离子的个数；z为颗粒表面离子价数；T为绝对温度；ε为介质的介电常数，ε水=78.5ε0，ε0为真空介电常数，取8.854 187 8×10-12F/m；φ0为颗粒表面电位，V；e为基原电荷。

对于低电位，斥能VR表达式可简化为

(3)

结合式(1)和式(2)，可得综合作用能V(VA+VR)为

(4)

根据文献[17]，颗粒间综合作用能V随颗粒间距离变化关系如图1所示。图1中曲线表示的是综合位能(即斥能与引能的代数和)与颗粒间距之间的函数关系，则曲线斜率代表着颗粒间的综合作用力。当曲线斜率向上时，颗粒间综合作用力表现为斥力；当曲线斜率向下时，颗粒间综合作用力表现为引力，势垒所在位置正是曲线斜率的转折点。当颗粒在越过势垒后，曲线斜率开始逐渐向下，颗粒间的综合作用力将持续表现为引力，在引力作用下颗粒将进入絮凝过程，故以此位置作为絮凝发生的标准。

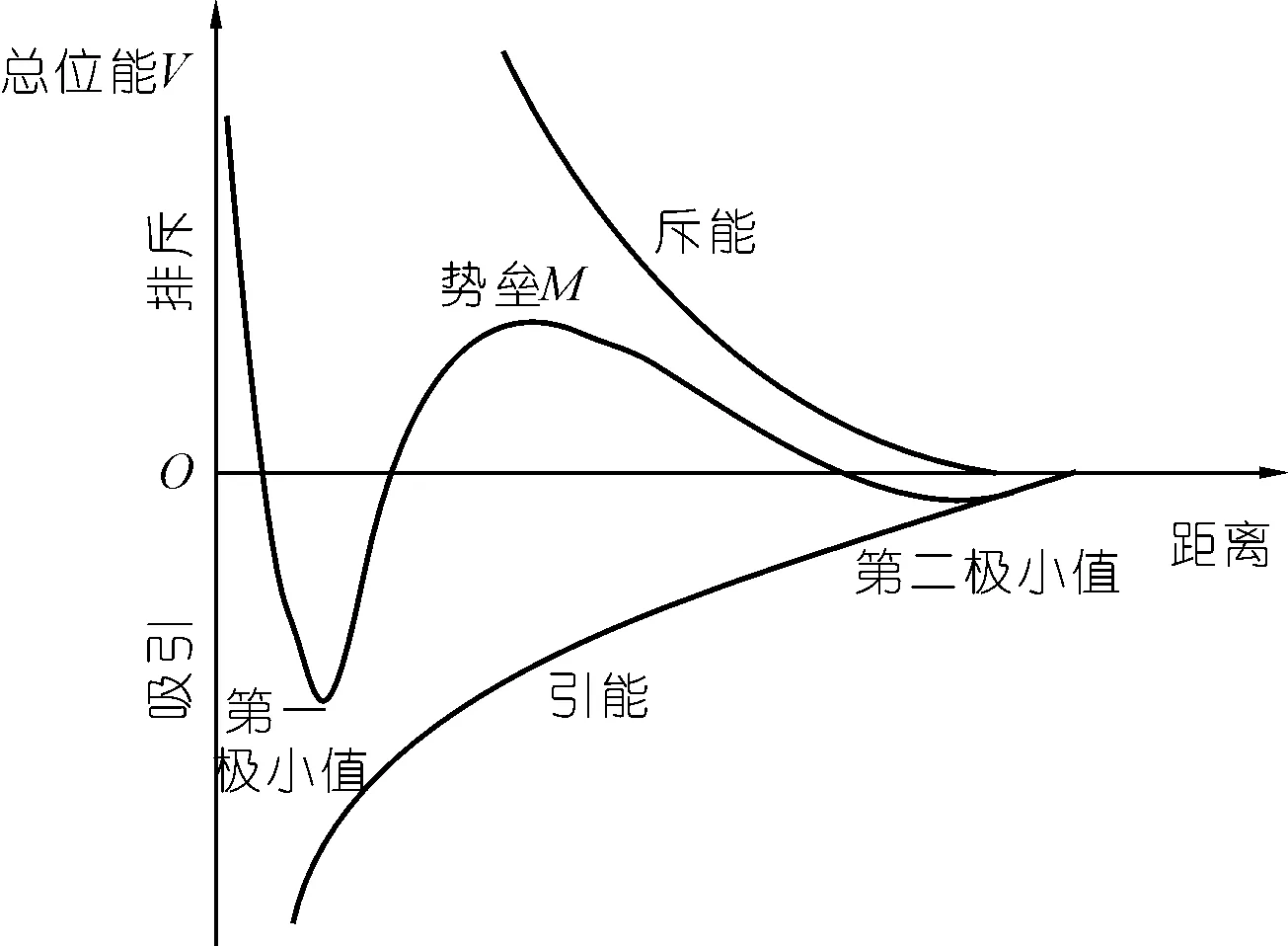
图1 总位能曲线Fig.1 Total potential energy curve

由图1可看出：在势垒高度M处，综合作用能取得极大值，对式(4)求导并令其等于0可得：

(5)

式中：rm0表示势垒所在位置对应的颗粒间距。

把式(5)代入式(4)，可得势垒高度M表达式：

(6)

由图1可知，势垒高度M>0，也即1-κrm0>0，即：

rm0<κ-1

(7)

式(7)表明：颗粒表面间的距离在小于双电层厚度时，才能越过势垒位置，同时也意味着絮凝的开始。从数量级来看，rm0值与κ-1值相当、且κ值随着浑水体系的电解质种类、离子浓度改变而变化，两者间的等量关系可反应出rm0值与水体性质间的联系。令

rm0=βκ-1

(8)

式中：β是与电解质浓度、泥沙含量等水体性质有关的系数。

将式(8)代入式(6)，得：

(9)

本文所用符号较多，现增加一符号说明表用于解释说明符号含义，见表1。

表1 符号说明Tab.1 Symblo description table

2 泥沙絮凝动力学模式推导及其验证

2.1 泥沙絮凝动力学模式

假设在水沙浑水体系中(见图2)，存在以某一中心泥沙颗粒为圆心、半径为r(大于泥沙颗粒半径d/2，小于絮团半径dx/2)的球面；在单位时间内，体系中泥沙因布朗运动从球面外进入球面内的泥沙颗粒数量为J0；根据Fick第一定律，有：

(10)

式中：S是球的表面积，即S=4πr2；D是扩散系数，m2/s；C为球面界面处泥沙浓度，单位为单位体积内泥沙颗粒数量，其表达式为

(11)

式中：SV为体积含沙量。

图2 中心颗粒(红色)及球面二维示意Fig.2 Two-dimensional schematic diagram of central particle(red)and spherical surface

由DLVO理论可知，泥沙颗粒相互碰撞后，能否发生絮凝取决于颗粒间的距离能否越过势垒位置。由于泥沙颗粒间的斥力对泥沙颗粒的聚集起阻碍作用，为了定量描述泥沙颗粒间的这种斥力影响，文献[17]给出了阻力因子JC表达式：

(12)

式中：α表示单一颗粒进入球面后与其它颗粒的碰撞次数，f为阻力系数，其他符号意义同前。

阻力因子JC的物理意义为，由于势垒的存在引起球面的泥沙颗粒个数。则单位时间内，体系中从球面外净进入球面内的泥沙颗粒数量J的表达式为

(13)

变化形式得：

(14)

解此微分方程，得：

(15)

当r=d时，即中心颗粒外侧紧密包含一层泥沙颗粒，可认为α=1，C=0(因为颗粒紧密接触后即失去其自由运动本性)，代入式(15)得：

(16)

式中：M为势能曲线的势垒值，b为积分常数。

当r=dx/2时，即球面边缘处，可认为此处泥沙浓度C等于体系内的泥沙浓度，代入式(15)得：

(17)

联立方程(16)～(17)，可得：

(18)

势垒高度M值一般较Df值大得多，故上式可简化为

(19)

根据斯托克斯定律可知，阻力系数f表达式如下：

f=3πηd

(20)

式中：η为液体的黏滞系数。

假设泥沙絮凝过程结束后，细颗粒泥沙均是以絮团形式存在，且单位体积内共有絮团数目m，每个絮团中泥沙颗粒数量相等，均等于N，则：

(21)

式中：SV0为初始体积含沙量，N为单个絮团中泥沙颗粒数量。

根据Feder等[18]的研究，絮团中泥沙颗粒数量N满足以下关系式：

(22)

式中：Df为絮团的分形维数，其他符号意义同前。

体系中单位体积内通过球面并发生絮凝的颗粒总数Jm，等于单一球面内发生絮凝的泥沙颗粒数量J与絮团数目m的乘积，表示式为

(23)

此外，由C的定义可知：

(24)

将公式(24)代入公式(23)，即：

(25)

把式(11)代入式(25)，可得：

(26)

则絮凝速率系数KF表达式为

(27)

对公式(26)进行积分，可得泥沙絮凝动力学方程为

(28)

根据公式(28)，可知半衰期t1/2

t1/2=ln2/KF

(29)

则泥沙絮凝沉降平均速度ω为

(30)

也即：

(31)

式中：h为泥沙沉降高度。可以看出，絮凝速率系数KF与絮凝沉降平均速度ω呈正相关关系。

2.2 参数值确定

采用文献[19]的实验结果确定公式(27)的相关参数。在文献[19]的静水絮凝沉降实验中，泥沙浓度选为10 g/L；氯化钙浓度分别为0，0.3，0.6 mmol/L和1 mmol/L；泥沙浓度用吸管法测定，取样点位置位于液面下20 cm处，所得结果换算为与初始泥沙浓度的相对值，即SV/SV0。根据陈洪松等[19]实验研究发现，泥沙相对浓度SV/SV0随时间呈指数变化。故本文以氯化钙浓度为0.3 mmol/L的实验数据为例，以相对浓度倒数的对数值ln(SV0/SV)为纵坐标，以时间t为横坐标，实验散点应拟合为一条倾斜的直线，直线斜率即为絮凝速率系数值(见图3)。

图3 泥沙相对浓度的变化规律Fig.3 Variation law of relative sediment concentration

由拟合结果可知，本次试验组的絮凝速率系数值为0.020 8。此外，Kim等[20]通过在碰撞效率函数中引入捕捉概率函数，求解出絮团的粘结概率θ范围为(5.03～6.50)×10-3。黏结概率θ指的是颗粒经多次碰撞后粘结在一起的可能性大小，而系数α表示是颗粒间的碰撞次数，因此在数值关系上θ=1/α，据此可取α=199。由于在文献[19]中缺乏对絮团尺寸与分形维数的测量，因此参考文献[8]的理论研究，N值取为120。综合以上参数值，根据公式(27)求得扩散系数D=8.866×10-10m2/s。

2.3 公式验证

采用文献[19]中氯化钙浓度为1 mmol/L的泥沙浓度观测结果对本文公式(27)进行验证，所得结果见图4。图中纵横坐标均采用对数值ln(SV0/SV)。

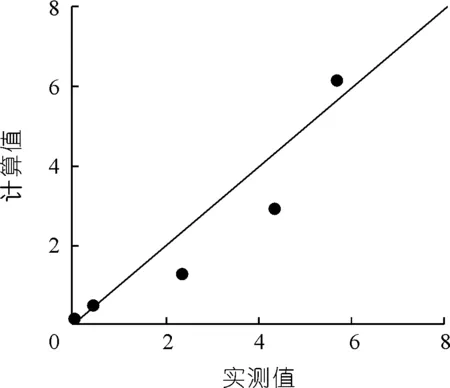
图4 泥沙相对浓度的计算值与实测值对比Fig.4 Comparison of calculated and measured values of relative sediment concentration

由图4可见，计算值与理论值较好吻合，为进一步分析评价公式的计算精度，本文采用均方差分析方法进行评价。

(32)

式中：RMS为均方根相对误差值，RMS越小表示计算精度越高；uCi为计算值；uMi为实验值；n为样本个数。

经计算得知本次RMS为0.364，表明该公式计算精度较高。相对于关许为[11]和陈洪松[12]等通过实验数据拟合所得到的絮凝动力学模式方程，本文注重理论推导，依托于DLVO理论和Fick第一定律，通过引入球形模型，可描绘出泥沙絮凝发生过程；另外影响因素考虑较为全面，推导出的絮凝速率系数表达式中，将扩散系数、泥沙含沙量、离子浓度、分形维数和颗粒粒径等相关物理参数关联起来，更能体现出絮凝的实质。

3 结 论

(1) 在静水条件下，应用DLVO 理论分析泥沙颗粒间的力学关系，得知泥沙颗粒发生絮凝的条件是颗粒能否越过势垒。

(2) 根据Fick第一定律，推导出絮凝速率系数表达式及絮凝动力学方程，即建立了体系内泥沙浓度随时间变化关系式，经实测资料验证公式吻合良好，且理论基础完善。

本文主要探讨在布朗运动下的泥沙絮凝沉降过程，研究对象为均匀细颗粒泥沙，对于非均匀沙的絮凝沉降规律，仍需作进一步研究。