基于有效度评价的隧道最大涌水量预测模型研究
殷 保 国,左 昌 群,李 庆 年,肖 艳 艳
(1.中国地质大学(武汉) 地质调查研究院,湖北 武汉 430074; 2.中国地质大学(武汉) 工程学院,湖北 武汉 430074)
0 引 言
随着中国交通基础建设的快速发展,隧道工程的数量、规模日益增加[1],遇到的地质条件也越来越复杂,其中,隧道涌水是工程建设中最为突出的不良地质灾害之一。如2018年佛山地铁2号线突发透水事件、2019年云南省临沧市安石隧道突泥涌水事故等,引发了人员伤亡、财产损失以及生态环境恶化等一系列问题,对隧道的安全施工造成了严重的影响[2-5]。为了防范和治理地下水灾害,迫切需要运用科学的方法预测施工隧道的涌水量,并制定有针对性的施工处治措施[6-7]。
目前,国内外学者围绕隧道涌水量预测进行了大量的理论与实践研究[8-13],其中,解析法仍然是目前隧道在选线、勘察、设计阶段最广泛使用的涌水量预测计算方法,广大学者也针对不同隧道条件提出了多种计算方法和预测模型。谢伟等[14]基于裘布依理论公式对折多山隧道的涌水量进行预测汇总,进而预测出集中涌水段落,提出了施工过程中的防治措施。魏兴萍等[15]基于铁路勘测规范经验公式计算出重庆市南山隧道的涌水量,分析出了南山隧道涌水半径积雨面积小的原因,以及提出了相对应的施工措施及建议。但由于隧道涌水的影响机制复杂,单个预测公式未能有效地整合所有因素,不可避免地会造成一定的偏差[16]。为了解决这一难题,对既有的预测模型进行组合,通过构建新的涌水量预测模型,规避单个预测模型带来的偏差影响,以达到最佳的预测效果[17],是目前研究的主要方向。然而,对于组合预测模型的选择上还是比较随意,主要是通过工程经验和工程类比来进行选择,主观性太强,从现有研究结果来看,对于组合预测模型的效果评价也缺乏相应合理的指标。目前,国内已尝试引入有效度指标来筛选组合预测模型[18-20],剔除冗余模型[21],使其预测结果更为准确,精度更高。基于有效度评价的组合预测方法在其他领域也已经产生一定的应用和成果[22-25],但是在工程上面应用,尤其是隧道涌水量上预测还是比较少。
因此本文结合广州地铁21号线矿山法隧道工程,以隧道最大涌水量为评价对象,用8种常见的模型作为基本预测模型,基于组合预测思路,引入有效度指标,对单个涌水量计算模型进行了有效度排序,用有效度最高的模型作为基本模型,按照有效度由高到低依次与其进行组合,剔除冗余模型,选取最优模型进行组合预测,并将预测结果与实测结果对比,对涌水量预测模型进行评价分析。
1 隧道最大涌水量组合预测流程
1.1 组合预测模型的内涵
组合预测模型是一种综合考虑各单项预测方法,将多种预测方法赋予不同的权重而组合形成的综合模型,与单一的预测模型相比,能够充分利用各种模型的优点进行合理预测,有效提升预测精度和预测能力。自1969年国外学者Bates等[26]率先提出组合预测模型以来,该模型凭借其自身的科学性和预测的准确性,使得组合预测技术在工程、农业、信息等领域得到了较快的应用和发展。
1.2 组合预测模型的构建
(1) 首先,计算单个模型预测结果的误差,在满足权重归一化的情况下,给予单个预测模型一定的权重比例,然后组合预测模型构造目标函数。具体的组合预测模型可以表示如下:
max(min)Z=F(k1,k2,k3,…,kp)
(1)
式中:F(k1,k2,k3,…,kp)即为目标函数,为预测模型中的误差大小;k1,k2,k3,…,kp为p种单个预测模型中的权重比例,满足非负性。
(2) 将单个预测模型按照一定的权重组合起来的方式有两种,线性组合和非线性组合。
如若组合预测模型f=k1f1+k2f2+k3f3+…+kpfp,那么则称f为线性组合;如若组合预测模型f=μ(k1,k2,k3,…,kp),其中μ为非线性函数,那么则称其为非线性组合。
通过对各个涌水量预测模型进行对比评价,用合理的权重系数构建组合预测模型,在一定程度上能够弥补单一方法考虑因素不足的缺陷。
1.3 有效度评价模型与冗余模型

令涌水量组合模型的精度矩阵为
(2)
定义称第j种涌水量预测方法的预测有效度[27]为
Gj=E(Aj)(1-σ(Aj))
(3)
式中:E(Aj)为第j种涌水量预测方法的预测结果精度的数学期望,σ(Aj)为第j种涌水量预测方法的预测结果精度的标准差。
(4)
(5)
E(Aj)表示的是第j涌水量预测方法在不同观测点的预测结果的平均精度,其值越大越好,而σ(Aj)表示的是第j种涌水量预测方法在不同观测点的预测结果的不稳定性,值越小越好。
若参与组合的涌水量预测模型由p增加至p+1后,并不能够提高预测结果的预测精度,则称此类模型为冗余模型。若加入的模型和加入前的最优组合预测方法的误差协方差小于加入后的误差平方和,那么新加入的模型一定能够减小预测误差的平方和;否则,该模型为冗余模型。
基于以上分析,本文从预测有效度的角度给出如下定义:部分新加入的模型不能够使得原有的单个涌水量预测模型或组合模型的预测有效度提高,则将此类模型称为冗余模型。
因此,在挑选单个涌水量预测模型时,当涌水量组合模型的有效度增加时,则保留该涌水量预测模型;否则,该模型为冗余模型,应该将其从预测模型中予以剔除。
1.4 涌水量预测计算流程
本文提出基于预测有效度的组合预测隧道涌水量模型的筛选及计算流程,阐述如下:
(1) 按照上述定义的有效度原则,依次对单个涌水量模型的有效度进行计算,并依据计算结果对其进行评价排序,不妨设G(f1)≥G(f2)≥…≥G(fp)。
(2) 选取出有效度最高的两个涌水量预测模型,即f1和f2,将他们按照误差平方和最小原则给予一定的权重比例,进行组合预测,设为f12。将涌水量组合预测模型f12再对同样的断面进行预测,并计算它的有效度G(f12)。如若G(f12)≥G(f1),则说明模型f2的加入能够使得涌水量的预测更加精确,则保留该涌水量预测模型;如若G(f12)≤G(f1),说明模型f2的加入使得涌水量预测的有效度降低,预测精度下降,则f2为冗余模型,应予以剔除。
(3) 重复步骤(2) 的流程,按照有效度由大到小的顺序,依次往组合模型中添加单个涌水量预测模型,计算组合后的有效度G后与组合之前的有效度G前进行对比判断,直到有效度最低的单个涌水量计算模型fp加入后计算完成。
(4) 在所有模型都添加计算完之后,最终得到的模型即为有效度最高预测精度最高的组合预测模型。
涌水量计算流程如图1所示。

图1 最大涌水量组合预测计算流程Fig.1 Flow chart of combined forecasting calculation of maximum gushing of water
2 工程实例
研究区为广州地铁21号线第12标段长平-金坑区间,起讫里程DK22+127.000~DK28+054.000。区间共有2段隧道,1号隧道起讫里程为DK22+470~DK23+748,2号隧道起讫里程为DK25+052~DK27+610,总里程为3 836 m,隧道采用矿山法开挖。隧道工程地质剖面如图2所示。

图2 隧道工程地质剖面图Fig.2 The geological profile of tunnel engineering
2.1 工程地质特征
2.1.1地形地貌
研究区属低山丘陵夹山间谷地地貌,低山丘陵区沿线地形坡度约30°~55°,地面高程约32.1~240.0 m,隧道段最大埋深为113.7 m。
2.1.2地层岩性
研究区岩土层主要包括:① 覆盖土层,包括填土层和第四系松散沉积物,主要为人工填土层、冲洪积的砂、卵石、粉质黏土、残积砂质黏性土。② 下伏基岩包括晚三叠系(T3ηγ)花岗岩、晚侏罗系(J3ηγ)花岗岩、晚志留系(S3ηγ)花岗岩以及元古界(Pt)花岗片麻岩。隧道洞身段围岩主要为中-强风化的花岗岩。
2.2 气象水文
2.2.1气象特征
研究区属南亚热带季风型气候,气候温暖潮湿,日照充足,热量丰富,长夏无冬,雨量丰沛,干湿季明显。多年平均降雨量1 835 mm。夏季多暴雨,每年4~9月为汛期,占全年降雨量的88.2%,年平均蒸发量1 432.2~1 738.5 mm。
2.2.2地表水
研究区内除一些人工沟渠及间歇性溪流外,无大的常年性河流。线路区间起点临近水西涌,宽度约14.0 m,现场调研期间水深约1.5 m。
2.2.3地下水
研究区地形起伏大,地下水水位埋藏差异较大,水位埋深为0.10~32.40 m,平均7.93 m,地下水位的变化与地下水的赋存、补给及排泄关系密切,并受季节变化影响。地下水按赋存方式可分为第四系松散岩类孔隙水和块状基岩裂隙水。地下水径流以垂直循环为主,具有埋藏深、径流途径短,补给区与排泄区接近一致的特点。
3 涌水量预测过程与结果
3.1 计算断面选择
结合现场实测方案布置,从研究区中选取8段典型隧道断面进行预测。8个断面的工程地质条件及相关参数选值如表1所列。

表1 计算断面预测模型参数Tab.1 The prediction model parameters of the calculating section
3.2 计算模型初步筛选
选取8种常用的隧道最大涌水量计算模型,构成方法集ω。8种预测模型依次是Goodman(1965)模型、Karlsrud(2001)模型、Schleiss(1988)和Lei(1999)模型、Lombardi(2002)模型、大岛洋志模型、王建宇(2003)模型、铁道勘察规范模型以及苏凯等(2017)模型。各模型的计算公式如表2所列。

表2 预测模型及计算公式Tab.2 Prediction models and calculation formula
3.3 最大涌水量单项预测及评价
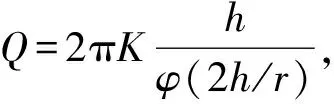
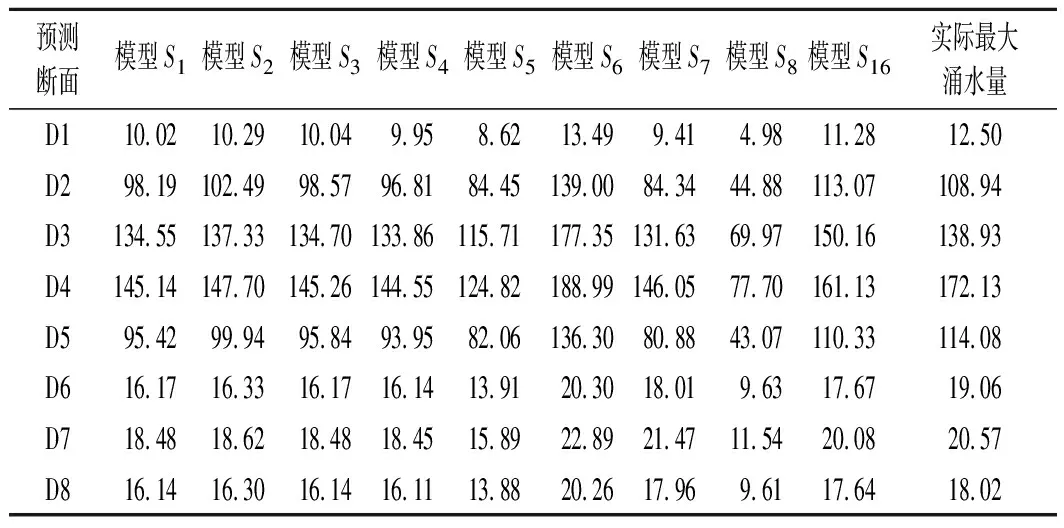
表3 各模型的最大涌水量预测结果Tab.3 Maximum gushing of water predicted by the models m3/d

图3 φ(2h/r)随2h/r变化的关系Fig.3 The relationship between φ(2h/r) and 2h/r
3.4 单项预测模型有效度评价
根据公式(3)对每种预测模型的有效度G作进一步的定量分析,结果如表4所列。
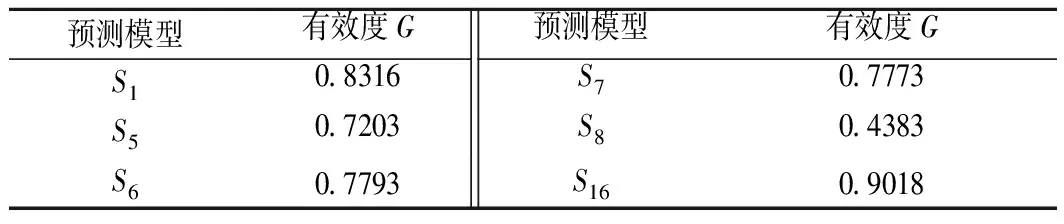
表4 各模型的有效度Tab.4 Effectiveness of each model
由表4可知:Goodman(1965)模型的有效度最大,其次为王建宇(2003)模型、铁道勘察规范模型和大岛洋志模型,而苏凯等(2017)模型的有效度最小,故5种预测模型的精度由高到低排序如下:
G1>G6>G7>G5>G8
(6)
3.5 组合预测模型有效度评价
结合前文结果,先利用有效度最高的两个单测模型S1和S6建立线性组合模型,记为S16,根据误差平方和最小原则,用Matlab编程,计算出S1和S6的权重为0.635 3和0.364 7,故组合模型建立为
xt=0.6353x1t+0.3647x6t,t=1,2,…,8
(7)
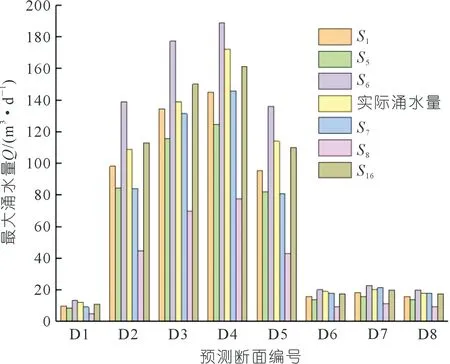
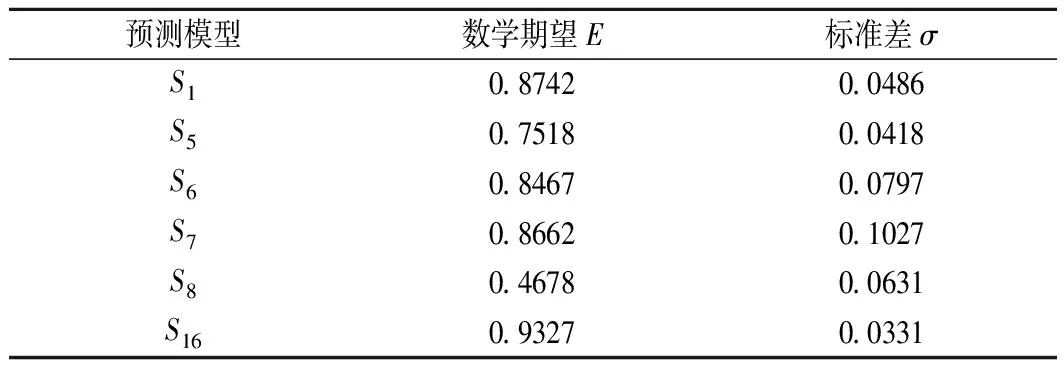
由该组合模型计算出8个点的最大涌水量,从而计算出该模型的有效度,可得G16=0.901 8,可以发现G1 xt=0.3735x1t+0.4028x6t+0.2238x7t, t=1,2,…,8 (8) 计算出有效度G167=0.885 8,可以发现G167 xt=0.6353x1t+0.3647x6t,t=1,2,…,8 (9) 为了验证上述最优组合模型的精确性与有效性,将上述模型计算出来的最大涌水量结果、方法集ω中的S1,S5,S6,S7,S8与现场实测的单位长度的最大涌水量进行了对比,同时计算出各预测模型的数学期望E和标准差σ,结果如图4、表5和表6所示。 图4 不同模型的预测结果对比Fig.4 Comparison of prediction results of different models 由上面的计算结果可知,苏凯等(2017)模型的预测结果远小于实际的最大涌水量,王建宇(2003)模型的预测结果大于实际的最大涌水量。但综合来看,Goodman(1965)模型、王建宁(2003)模型和组合模型的预测结果接近于最大涌水量,而组合模型是由Goodman(1965)模型和王建宁(2003)模型线性组合而成。6种预测模型的精确度由高到低依次是S16>S1>S6>S7>S5>S8,与有效度的排序保持一致,且组合模型S16的数学期望E大于单项预测模型,标准差σ小于单项预测模型,说明该组合模型在不同观测点的预测结果的平均精度和不稳定性均优于单项预测模型。 表5 不同模型的预测结果误差对比Tab.5 Error comparison of models prediction results % 表6 各模型的数学期望和标准差Tab.6 Mathematical expectation and standard deviation of each model 由此可知,由单项预测模型综合而成的预测组合模型的精度超过最佳的单项预测模型,但并非组合模型中单项预测模型的数量越多越好,而是需要通过合理的筛选。因此,按照有效度从高到低的顺序选取单项预测模型,计算出组合模型的有效度,可以有效地避免冗余模型的加入影响组合预测模型的准确性。 (1) 本文采用8种不同的预测模型对研究区的最大涌水量进行了计算,通过合理的筛选单项预测模型,由组合预测模型算出来的最大涌水量的平均准确率高达94.63%。 (2) 有效度是评价单项预测模型加入到组合预测模型后,能反映组合预测模型预测结果精度的指标。本文的研究以有效度为衡量标准,一定程度上解决了单项模型的筛选问题,避免了冗余模型的加入,为提高组合模型预测的精度提供了一种有效的处理方法。 (3) 与此同时,利用误差平方和最小准则,给予各单项预测模型一定的权重比例,以有效度作为预测模型预测结果精度的指标,剔除了冗余模型,有效的利用了有效度较高的单项预测模型,达到了提高预测模型整体预测精度的效果。3.6 最优组合模型验证
4 分析与讨论

5 结 论

