条形基础下成层砂土地基破坏机理及承载力计算

陈 华，沈 军 辉

(1.四川省交通勘察设计研究院有限公司，四川 成都 610059； 2.成都理工大学 地质灾害防治与地质环境保护国家重点实验室，四川 成都 610059)

0 引 言

自从Terzaghi[1]发表关于均质地基上浅基础承载力估算理论以来，许多研究人员对天然地基承载力进行了研究。然而，问题的复杂性导致层状地基上浅基础的承载力估算的难度较大，所推导出的封闭形式塑性解十分繁琐，不便于工程应用。因此，提出简单的承载力表达式是十分有必要的。现有的研究成果多集中在软黏土上的密实砂土地基：Meyerhof[2]首先采用半经验方法计算了软黏土上覆致密砂的条形和圆形基础的承载力，并且同时考虑了硬黏土上覆疏松砂的情况。Meyerhof提出的冲剪模型后来在许多试验、数值分析和解析法分析研究中得到了改进，主要改进者包括Hanna和Meyerhof[3]、Griffiths[4]、Das和Dallo[5]、Michalowski和Shi[6]、Kenny和Andrawes[7]、Burd和Frydman[8]、Okamura等[9]、Shiau等[10]、秦会来[11]、Salimi等[12]。

与单层砂土地基相比，成层砂土地基力的传递更为复杂，得出封闭解析解的难度很大，因此导致层状砂土地基上浅基础承载力的相关研究工作较少。比较经典的方法为建筑研究指南BRE 470-2004[13]中的方法和Hanna[14]提出的半经验方法。实际上，BRE 470-2004中的方法是Hanna方法的简化，而Hanna方法又基于Meyerhof的冲剪模型。基于特定的简化地基破坏模式，研究人员采用极限平衡和极限分析方法对成层砂土地基的承载力计算问题进行了研究。Ghazavi和Eghbali[15]对Richards等[16]提出的地基失效模式进行了扩展，推导得出两层砂土地基上的承载力系数。对于两层黏性土上的基础，Purushothamaraj等[17]得到了上限解析解。Florkievicz[18]、Huang[19]、Khatri[20]等使用有限元塑性极限分析方法(FELA)计算极限承载力的上下限，在计算过程中可以结合使用圆锥优化方法[21-24]。此外也可以通过试验方法对成层砂土地基承载力进行研究，如Hanna[14]，Das和Munoz[25]，Kumar等人[26]进行了层状砂土地基的缩尺模型试验研究。然而，考虑到砂土力学性质与围压应力水平的相关性，比例效应可能导致高估极限荷载[27-28]，因此缩尺模型试验的结果不能盲目推广到现场足尺地基的情况，但是可以采用试验结果对地基失效模式及机理进行探索。

为明确成层砂土地基失效破坏机理及相应的地基承载力计算方法，考虑不同的几何参数和土体力学参数，本文对成层砂土采用有限元塑性极限分析方法(简称FELA方法)进行了一系列分析，除了得出极限荷载的上限和下限外，还分析了地基破坏机制随几何参数和土体力学参数的变化。在与已有成果进行对比的基础上，本文提出一种实用方法以确定过渡破坏模式下成层砂土地基上条形基础的承载力。

1 层状砂土地基承载力计算的冲剪模型

如前所述，Hanna[14]将Meyerhof[2]所提出的半经验冲剪模型推广到了松砂上覆密砂浅基础的情况。基础沿图1所示假定的上层砂土中破坏锥形插入底层砂层中，底部砂土发生剪切破坏。地基承载力包括上部砂层和下部砂层的极限抗剪强度两部分。具体地，上部砂层的贡献与作用在如图1所示垂直破坏面上的被动压力PP有关，其大小取决于破坏面上的动摩擦角δ。被动压力PP可表示为

(1)

式中：γ1表示上部砂层重度；H和D分别表示上部砂层厚度和基础埋深；KP表示侧向土压力系数。底部砂层的贡献等于图1所示的均质砂土上虚拟基础的极限承载力qb。因此，层状砂上条形基础的承载力qu为

(2)

式中：qb和qt分别表示均匀松砂和致密砂层上条形基础的承载力，对应的埋深分别为H+D和D。

qb=0.5γ2BNγ2+γ1(H+D)Nq2

(3)

qt=0.5γ1BNγ1+γ1DNq1

(4)

图1 冲剪破坏示意Fig.1 Schematic diagram of punching shear failure

式(2)表明，承载力qu不能超过位于均质密实砂上的地基承载力qt。因此应该存在一临界厚度Hcr，一旦超过Hcr，底层砂土的性质将不影响地基承载力，而地基破坏完全发生在上层砂土中。式(3)和式(4)中的承载力系数Nγ2、Nq2、Nγ1和Nq1可以根据文献[29]计算。综合式(1)和式(2)易得

(5)

式(5)中的一个十分关键的参数为动摩擦角δ，它不恒定，而是随着上层砂土的厚度而发生变化[2]。Hanna[14]采用实验方法确定了δ的抛物线分布形式，其是两层砂土相对剪切强度的函数。为进行承载力qu简化估算，Hanna借鉴Meyerhof的方法，引入抗冲剪系数KS，令

KStanφ1=KPtanδ

(6)

则式(5) 转化为

(7)

其中，抗冲剪系数KS可以通过上层砂土内摩擦角φ1和下层砂土内摩擦角φ2由Hanna提供的图得出[14]。

BRE 470-2004指南采用了基于上述冲剪模型的方法，并且引入一些偏保守的假设：①在计算底部砂土对承载力贡献qb时，将埋深D取为0，忽略超载项γ1HNq2的影响；② 动摩擦角取为δ=2φ/3，Kptanδ项使用库仑被动土压力系数计算；③ 采用Vesic[30]提出的承载力系数Nγ公式，该公式计算结果略大于Meyerhof[29]提出的公式。

当上层砂土厚度小于临界厚度时，通过BRE 470-2004指南方法估计的承载力值始终低于式(5)得出的承载力值，该方法可用于快速估算成层砂土地基承载力。然而，使用该方法的前提条件是成层砂土地基的失效模式为冲剪模式，这与工程实际并不一定符合。如当上层砂土厚度足够大时，失效模式应该为传统剪切模式，而且冲剪模式和传统剪切模式之间必然存在一过渡破坏模式。此外，地基失效模式应该与两层砂土的相对强度以及与上层砂土的厚度有关。因此开展成层砂土地基失效模式和承载力计算工作对具体工程设计具有很重要的指导意义。

2 有限元塑性极限分析

2.1 计算参数

极限分析法是一种严格确定地基极限承载力上限和下限的方法[31]。因为复杂的几何结构会得出复杂的方程，复杂的方程不容易得出解析解，因此这种方法最初的应用较为局限。而使用有限元法求解极限平衡方程，可将极限分析法的应用领域扩展到复杂几何和非均质土壤地层[32]，相应的方法可以称之为有限元塑性极限分析(FELA)方法。该方法可以求解得出极限荷载的上限和下限，上限和下限之差可以理解为实际极限荷载的误差。假设极限荷载精确解为上限qupper和下限qlower的平均值qult，则相对误差可定义为[33]：

(8)

本文采用FELA方法计算成层砂土上条形基础的承载力。为了减小承载力计算中的相对误差，采用自适应重划分网格技术[34]。采用FELA方法分析地基承载力时需要假定砂土中发生塑性变形，而且本构模型采用的是相关联流动法则。对莫尔-库仑屈服准则而言，这意味着砂土膨胀角等于内摩擦角，显然这种假设不符合粒状材料实际。虽然相关联流动法则这一假设会影响极限荷载的计算值，但影响程度有多大目前仍没有定量分析方法。Davis[35]建立了关联流动法则引起的极限荷载误差与运动约束度间的关系。Drescher和Detournay[36]建议使用如式(9)和式(10)所示的等效强度参数和关联流动法则计算非关联流动的岩土类材料的极限荷载的上限和下限。

(9)

(10)

式中：φ，ψ和c分别表示内摩擦角、膨胀角和黏聚力，而φ*，ψ*和c*分别表示等效摩擦角、等效膨胀角和等效黏聚力。

对双层砂土地基采用莫尔-库仑模型和相关联流动法则，基底位于表层砂土的顶部。基础和地基间采用库仑摩擦，摩擦系数取tanφ1。为将相对误差RE控制在5%以内，每次分析中采用4次自适应重划分网格迭代。边界条件包括地基底处的固定水平和竖向位移以及地基的左右边界处的固定水平位移。根据Salgado等的研究[33]，对每个模型进行两次求解，以获得极限承载力的下限和上限，并据此估算平均极限承载力。高功率耗散强度区域代表剪切破坏平面，节点的速度矢量图则描述了地基破坏机理[37]。具体在计算中所采用的几何参数和材料参数如表1所列。

表1 FELA方法计算参数Tab.1 Calculation parameters of FELA method

2.2 承载力计算误差

在保持其余参数不变的情况下(φ1=40°，B=3.0 m，γ1=18 kN/m3，γ2=15 kN/m3)，增大上层砂土厚度H和下层砂土内摩擦角φ2，使用FELA数值方法结合自适应重划分网格技术计算极限承载力的上限和下限，计算结果如表2所列。从表中可以明显看出，相对误差RE随着底层砂土抗剪强度的增加而增加，但仍低于控制误差5%。因此，极限承载力qult可以近似取上限qupper和下限qlower的平均值，即qult=(qupper+qlower)/2。

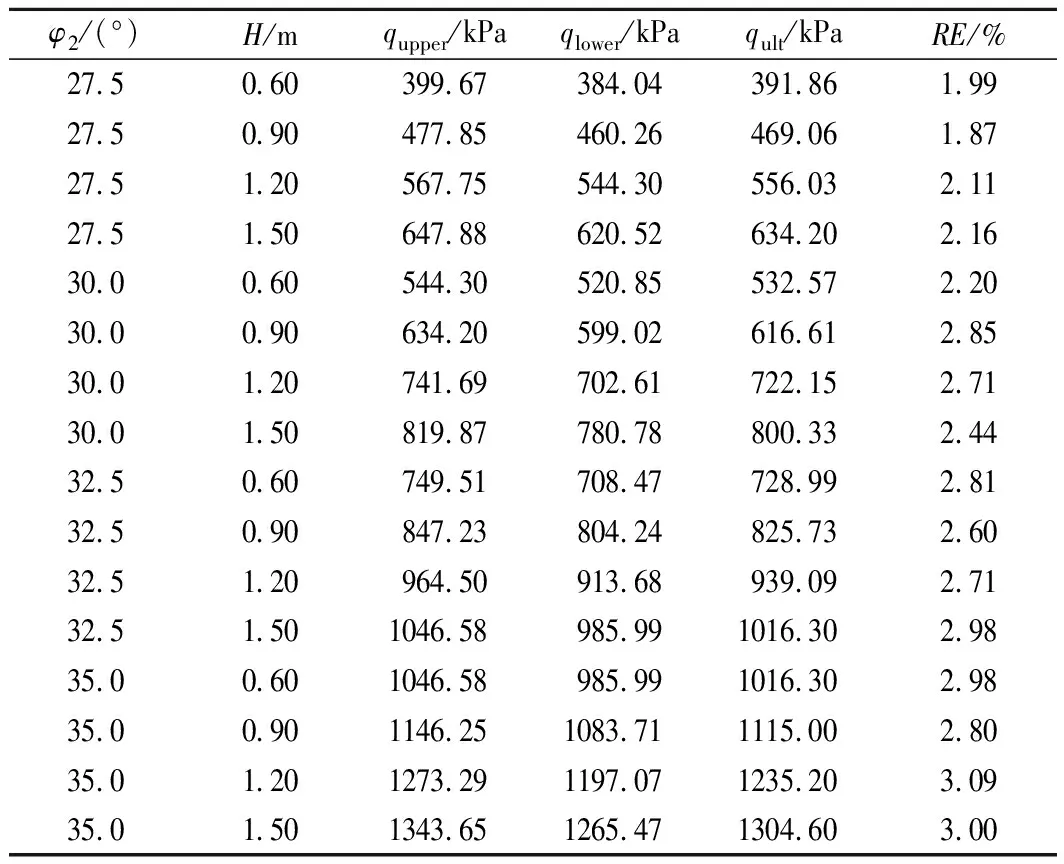
表2 FELA方法计算的极限承载力上下限及误差Tab.2 Calculation of upper and lower limits of ultimate bearing capacity and error by FELA method

2.3 计算结果对比及分析

为验证FELA数值计算方法的有效性并确定现有的半经验公式的适用范围，将FELA数值计算结果和试验结果、半经验公式计算结果进行对比。Meyerhof和Hanna[38]、 Das和Munoz[25]进行了成层砂土的物理模型试验，其中Meyerhof和Hanna[38]的试验采用0.05 m宽的条形基础，基底位于上层砂土表面，上层和下层砂土的内摩擦角分别为φ1=47.7°和φ2=34.0°，对应干重度分别为γ1=16.3 kN/m3和γ2=13.8 kN/m3。上层的相对厚度H/B取值从0～5.0，FELA计算结果与该试验结果的对比如图2(a)所示。Das和Munoz[25]的试验采用0.101 6 m宽的条形基础，基底位于上层砂土表面，上层和下层砂土的内摩擦角分别为φ1=43.0°和φ2=36.0°，对应干重度分别为γ1=17.06 kN/m3和γ2=15.25 kN/m3，FELA计算结果与该试验结果的对比如图2(b)所示。图2(a)和图2(b)中同时列出了Hanna[14]半经验计算方法和BRE 470-2004指南方法的计算结果对比。

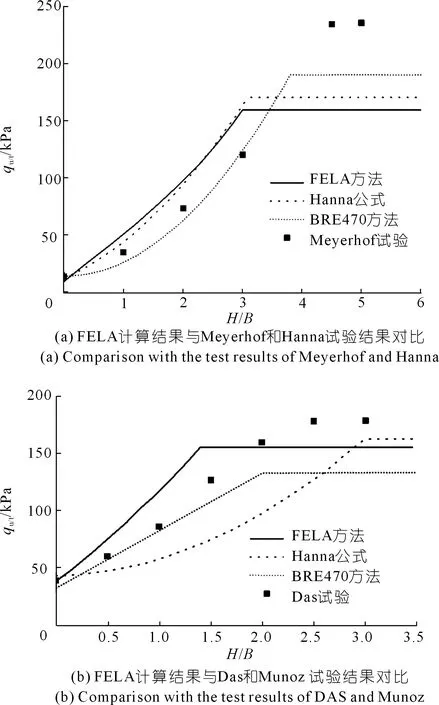
图2 FELA计算结果与试验结果和半经验公式计算结果对比Fig.2 Comparison of FELA calculation results with test results and semi empirical formula calculation results

如图2(a)所示，FELA方法和Hanna方法计算的承载力最为接近，当相对厚度满足H/B≤3时，试验结果与两种方法计算的结果较为吻合。当H/B≤3时，BRE 470方法计算值比较低，但与试验结果最为接近。当H/B>3时，即上部砂层厚度大于临界厚度时，即破坏完全发生在表层砂土中时，3种方法均低估了地基承载力，这可能是因为采用的是缩尺模型试验，而3种方法均假定砂土内摩擦角不随深度而变化。实际上，砂土表层由于固结应力较低因此摩擦角较高，在密砂中摩擦角随平均应力水平的变化更为明显[28]。因此，在缩尺模型试验中，基础宽度较小，对应的临界厚度也比较小，即使上部砂层厚度超过临界厚度也是比较薄的，在3种方法计算中均假定内摩擦角恒定，这显然会导致对极限荷载的保守预测。当H/B≤3时，表层密砂层对地基承载力的贡献相对较小，因此砂土摩擦角(包括膨胀角)与平均应力水平的非线性变化影响较小。从图2(b)中也可以得出类似的结论。当承载力不随着上层砂土的厚度的增加而进一步增加时即达到了临界厚度，通过FELA方法可以很好地得出临界厚度，而且临界厚度随着上层砂土内摩擦角的增加而增加。总体上，Hanna方法高估了地基承载力，BRE 470方法低估了承载力。

为明确分层砂土地基承载力发挥机理，选取FELA计算得出如图3所示的3种比较典型的地基失效机理图，速度云图间接反映了地基破坏机理。图3(a)～(c)所示的3种失效机制分别为：① 冲剪破坏机制，发生在上层砂土的剪切强度明显高于下层，且上层的厚度小于临界厚度的情况，该机制与Hanna[14]所考虑的破坏机制基本一致；② 过渡破坏机制，介于冲剪破坏机制和一般剪切破坏机制之间；③ 一般剪切破坏机制，上层砂土的厚度大于临界厚度的情况。

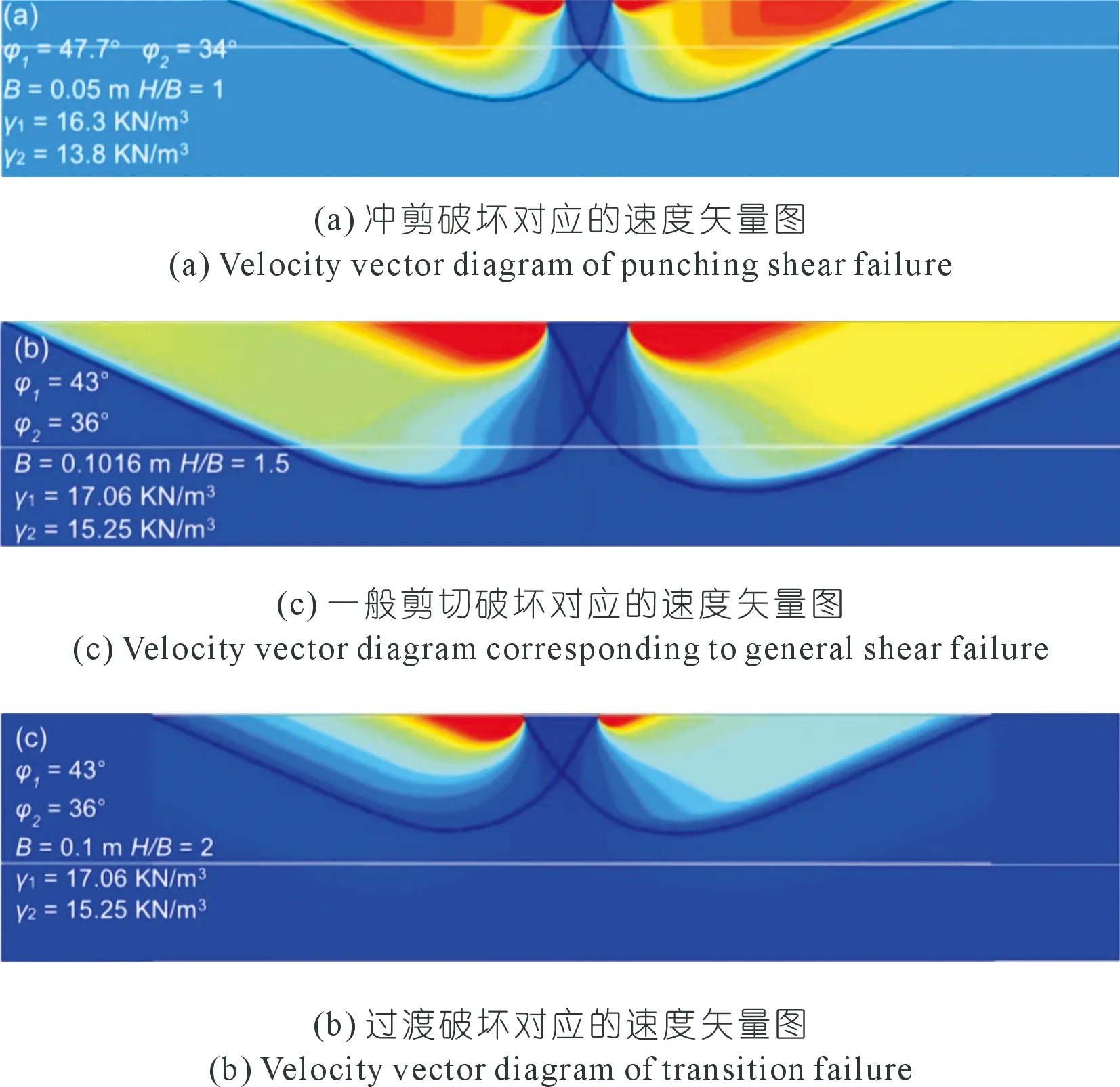
图3 成层砂土地基3种破坏模式Fig.3 Three failure modes of layered sand foundation

上述分析结果表明，冲剪破坏机制无法描述所有可能的破坏模式，考虑到冲剪破坏和一般剪切破坏均已有较为成熟的计算方法，提出一种适用于过渡失效机制的计算方法是十分有必要的。

3 承载力过渡失效模式计算

3.1 过渡失效模式机理

为了明确在满足何种情况下，地基失效模式会从图4(a)所示的冲剪模式转变为图4(b)所示的过渡模式，本文进行了如表1所列的大量FELA计算，从每次分析结果确定失效机理。具体地，可以用如图4(a)所示的上层剪切面的倾角θ来描述基底下形成的理想楔形，而倾角θ可以采用能量耗散强度等值线计算得出。倾角θ可以表示为砂层相对强度和相对厚度H/B的函数：

(11)

式中：倾角θ的单位为度；a，b和c是结合FELA计算结果进行函数拟合得出的参数，具体如表3所列。

图4 两种破坏模式示意Fig.4 Schematic diagram of two failure modes

表3 函数拟合参数

如图4(a)所示，根据式B′=B-2Htanθ结合式(11)计算等效宽度B′。当B′<0时即可能出现如图4(b)所示的过渡失效模式；B′>0即出现冲剪破坏模式。通过对FELA计算结果进行统计可以得出如图5所示的3种失效模式的分区，该图可以用来对失效模式加以判别。

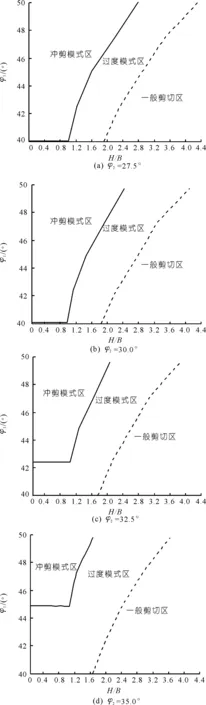
图5 3种失效模式分区Fig.5 Failure mode zoning

3.2 过渡失效模式对应的地基承载力系数

图5展示的3种破坏模式。冲剪破坏模式可以采用Hanna[14]方法，即式(7)加以计算；一般剪切破坏模式，可以采用均质砂土地基承载力计算方法加以计算；过渡失效模式缺乏相应的承载力计算方法。可以定义相应的承载力为

(12)

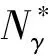
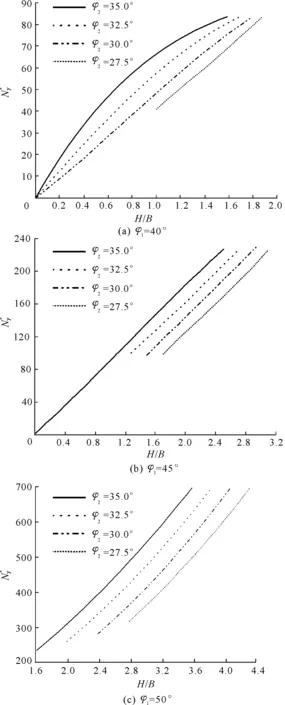
图6 过渡失效模式下的地基承载力系数Fig.6 Bearing capacity coefficient of foundation under transient failure mode

4 承载力确定流程

综上，对成层砂土地基在确定地基承载力前需先确定其剪切破坏模式，具体破坏模式的确定可以参考图5进行。冲剪破坏时的承载力可以按照式(7) 计算，过渡破坏模式的承载力按照式(12)计算，一般破坏模式可以采用传统土力学方法加以计算。

5 结 论

本文采用FELA方法研究了层状砂土地基承载力，然后借鉴前人的研究成果，采用理论分析法对地基破坏模式和承载力计算方法加以研究，得到以下结论：

(1) 层状砂土地基破坏模式可以分为冲剪破坏、过渡破坏和一般剪切破坏，当上层砂土的厚度不足以将破坏面包括在内但可以将锥形破坏锥体包括在内时发生过渡破坏模式。

(2) Hanna 方法和BRE 470方法只适用于冲剪破坏情况下地基承载力计算，而且BRE 470方法的地基承载力计算结果偏于保守。

(3) 本文所提出的过渡破坏模式下层状砂土地基承载力计算方法可以应用于具体的工程设计，具有校强实用性。