多尺度水泥基材料渗透性与孔隙关系模拟研究

赵 青，张 敏，李 宗 利

(1.黄河水利职业技术学院 水利工程学院，河南 开封 475004； 2.河南省小流域生态水利工程技术研究中心，河南 开封 475004； 3.西北农林科技大学 水利与建筑工程学院，陕西 杨凌 712100)

0 引 言

水泥基材料是由水泥水化产物与集料组成的复合材料，主要有砂浆和混凝土，具有多相多孔低渗透特性。其渗透特性主要决定于孔隙率的大小、孔隙尺寸以及孔隙连通等结构特征，而孔隙结构受水灰比、水化程度、龄期、养护情况、水泥浆与骨料界面孔隙等因素的影响[1-2]。混凝土水力渗透性能的试验方法包括水压力试验法、抗氯化物渗透试验法以及气体渗透性试验法等[3]。对于低渗透特性混凝土，由于水压法试验中难以形成稳定渗透，又多采用渗透深度法[3]、瞬态动力法等[4-6]，但这些方法不仅成本高、耗时长，而且结果离差性较大[7]，并不能从机理上揭示水泥基材料渗透系数与孔隙特征参数之间的关系。

关于水泥基材料的渗透特性与孔隙结构特征关系方面的研究，国内外已有大量的研究成果。Katz等[8-9]对沉积岩的渗透问题进行了研究，提出了渗透率与临界孔径、相对导电率的函数关系，计算结果与试验实测数据吻合较好。Garboczi[10-12]等根据压汞法得到的孔结构数据对Katz-Thompson方程进行了修正，并将该理论的适用范围拓宽到普通水泥石渗透性的研究中，试验结果表明，该理论适用于简单孔结构的岩石和孔隙率较大的混凝土。McLachlan[13-15]提出了GEM渗透理论，从水泥水化程度、孔隙率、水化产物的渗透率等因素出发，推导出了渗透率计算式。Lu等[16]通过试验，研究证明了GEM理论可适用于不同孔隙率的普通混凝土渗透系数计算。

上述文献所建立的水泥基材料的渗透率或渗透系数与孔隙结构关系，核心是需要孔隙的大小及其结构特征，但孔隙结构特征很难准确测定[17-19]，而数值模拟技术为其研究创造了条件。Koster等[20]应用水泥基材料的3D图像，并考虑未水化的水泥颗粒、水化过程及孔隙分布理论，利用自相似理论和“thinning agorithm”构建了水泥基材料孔隙空间模型，利用Hagen-Poiseuille定律计算裂隙内水流，从而模拟水泥基材料内水的运动，并基于达西定律得到了水力渗透系数。李守巨等[21]应用随机模拟技术研究了多孔介质渗透系数与孔隙率之间的关系，限于模型尺寸较小，而且未考虑孔隙的连通性。Sun等[22]通过扫描过渡区的2D孔隙结构，并以此为基础模拟出3D孔隙结构，但未能真实反映出孔隙连通情况。本文基于细观向上多尺度法，用蒙特卡罗法随机生成不同孔隙率的连续介质渗流分析模型，采用分级计算、逐级逼近的方式，实现了细观与宏观模型的材料参数传递。应用图型结构与Dijkstra算法，对随机生成的孔隙网络进行连通性判断，研究了低渗透性水泥基材料渗透性与其孔隙尺寸、孔隙率、等效孔隙率等特征参数间关系，揭示水泥基材料的水力渗透机理。

1 数值分析模型

1.1 向上扩展多尺度法

低渗透性水泥基材料中的孔隙尺寸一般在纳米到微米级[1]，属于微细观尺度上的研究。工程上所应用的水泥基材料尺寸一般较大，孔隙的分布和尺寸等细观结构对其宏观性能具有显著影响[23]。若按照孔隙的真实尺寸建立有限元模型，那么单元个数将超过千万，计算规模将会远远地超出微型计算机的能力范围，甚至无法实现。本文借助于向上扩展多尺度分析方法[24-26]，将宏观模型与细观模型相结合，通过细观模型向宏观模型中单元提供渗透性参数，采用分级计算、逐次逼近的方式，对模型的等效渗透系数进行分析，以研究其与孔隙率、尺寸等因素之间关系。

图1为渗流分析模型的分级示意图。图中，将计算模型分为4级分别进行渗流分析，分别记为i=1，2，3，4(下同)。i≤3级模型属于细观尺度，i=4级为宏观模型尺度。在第1级模型中，将随机分布的孔隙等效为一个单元或由多个单元组成的具有随机形状的大孔隙或裂隙(本文暂将孔隙和裂隙均称孔隙)，即1个单元就是1个独立孔隙或孔隙的一部分，高一级模型中单元的尺寸则取低一级模型的尺寸。对第1级模型孔隙单元的渗透系数运用裂隙立方定律[27]进行计算，其余模型中孔隙单元的渗透系数为低一级模型的等效渗透系数。因此在研究中，仅有第1级模型中的孔隙单元为真正意义上的孔隙，而其余各级模型中的孔隙单元均为内部含有孔隙的特殊“孔隙”单元。换言之，除第1级模型外，其余各级模型中所指的孔隙率只是一个相对值，并非绝对孔隙率。为了避免与真正意义上的孔隙率产生混淆，在本文中，将各级模型中孔隙体积与总体积的比值统称为相对孔隙率。

图1 渗流分析模型分级示意Fig.1 Classification of seepage analysis model

由文献[27]可知，当裂隙宽度在0.2 μm～1 mm范围时立方定律总是成立。Mehta的试验表明[28]：当混凝土的孔隙尺寸小于132 nm时，孔隙特征对其渗透性与强度均无影响。方赵峰等对标准试块(150 mm×150 mm×150 mm)进行的试验结果表明[29]，混凝土孔隙尺寸在100～1 000 nm时，对其渗透性贡献最大。基于以上研究成果，将第1级细观模型的等效孔隙尺寸分别定为0.5，1.0，1.5 μm，其余各级模型尺寸如表1所列。

表1 计算模型分级与尺寸Tab.1 The hierarchical models and sizes

在低渗透性水泥基材料中，孔隙多是片状裂隙，在此应用裂隙渗流立方定律计算其渗透系数，并假设裂隙壁面光滑，则第一级模型孔隙单元的渗透系数计算式为

(1)

式中：k1为等宽孔隙单元的渗透系数，m/s；ρ为水的密度，取103kg/m3；g为重力加速度，取9.8 m/s2；b为第1级模型等效孔隙尺寸，m；μ为水的动力黏滞系数，20 ℃时，μ=1.005×10-3Pa·s。在研究中，认为模型中的固体颗粒渗透性极低，取渗透系数ks为10-15m/s。表2为3种不同等效孔隙尺寸情况下等宽孔隙的渗透系数计算值。

表2 第1级模型孔隙单元渗透系数Tab.2 Pore unit permeability coefficient in first stage model

1.2 不同孔隙率模型的生成方法

在分析模型中，假设一个单元为一孤立孔隙或孔隙的一部分(对于第2～4级模型，此处指含孔隙的单元)，将孔隙的随机分布问题转化为单元材料属性随机赋值问题。采用Monte-Carlo法，随机生成孔隙单元号或含孔隙的特殊单元号，实现给定孔隙率下孔隙的随机分布。

1.3 孔隙连通性判断

应用Dijkstra最短路径算法[30]查找连通孔隙。每1个孔隙单元的单元号看作是图形结构中的一个顶点，单元与单元之间的关系为图形结构中边，由此构成空间拓扑结构。采用Dijkstra算法寻找出每个单元连通的最短路径，并输出最短路径的顶点(孔隙单元的单元号)，即可完成孔隙连通性判断问题。值得注意的是，采用Dijkstra算法寻找出的连通路径是最短路径，图2中，盲端孔隙只有储存水的作用，对渗透性并无贡献，因此，连通路径中不包含盲端孔隙构成的通道。

图2 盲端孔隙Fig.2 Deadend pores

1.4 分析模型建立及其模拟方案

假设条件如下：

(1) 渗流为稳定渗流，连续介质服从饱和介质达西定律，孔隙渗流符合光滑裂隙立方定律；

(2) 数值模型中每个单元均为各向同性材料，除孔隙单元外，每一级细观模型中的固体颗粒单元与最终的宏观模型中固体颗粒单元材料性质相同；

(3) 不考虑流体(水)、孔隙与固体颗粒单元的压缩性，渗流发生时模型的孔隙率不变，即不考虑流固耦合效应，其贮水系数为0。

各级模型的尺寸如表1所列。可以看出：模型尺寸在变化，但单元数均为20×20×20=8 000。单元采用三维8节点单元，初始孔隙水压为0。有限元模型的一个方向的2个面为已知水头边界条件，上下游面之间的水头差ΔHi(i=1～4)与模型尺寸Li相等；其余各面为不透水边界。

各级模型的相对孔隙率分别为n1，n2，n3，n4，基于向上扩展多尺度分析方法，细观模型是宏观模型的局部表现，故n1>n2>n3>n4，最终第4级模型(宏观模型)的总孔隙率ntotal，即模型的绝对孔隙率由式(2)计算：

ntotal=n1×n2×n3×n4

(2)

考虑到普通混凝土中的孔隙率含量较低，不大于0.2，一般在0.1左右[16]，因此，各级模型中所取的相对孔隙率ni以及最终的总孔隙率ntotal如表3所列。

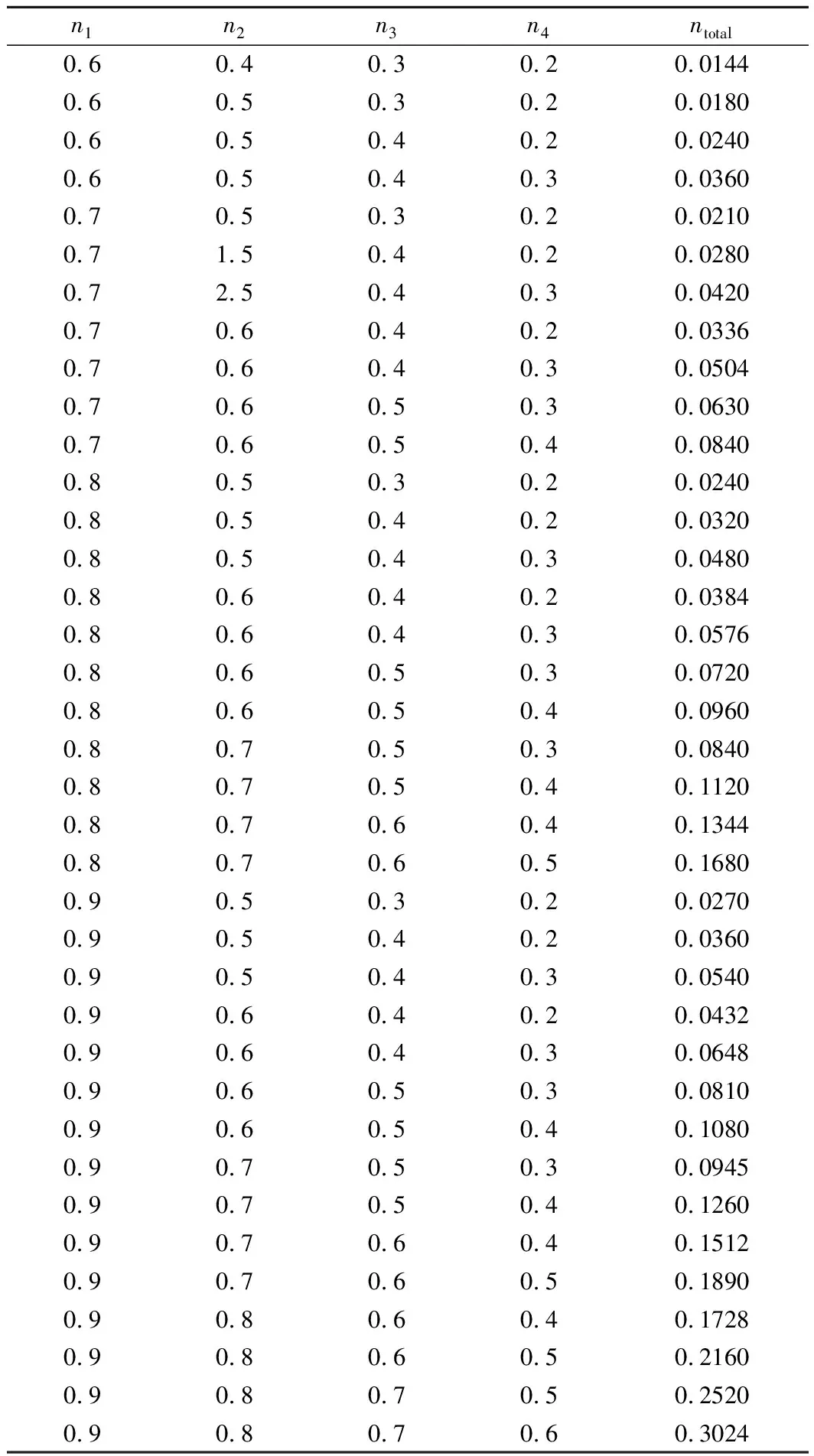
表3 孔隙率的选取Tab.3 Selection of porosity

2 渗透系数与孔隙率的关系

为了确定孔隙率、孔隙尺寸与其渗透性表征参数渗透系数之间的关系，在垂直于渗流主方向取切平面，通过切平面所有节点的流量积分，得到切平面的流量q，基于达西定律有：

(3)

式中：keq为等效渗透系数，m/s；ΔH为上下游水头差，m；L为模型尺寸，m。

2.1 渗透系数与孔隙率尺寸的关系

对孔隙尺寸为0.5，1.0，1.5 μm的219个各级模型结果进行分析，在不考虑孔隙连通性的情况下，将孔隙尺寸为0.5，1.0，1.5 μm所对应的等效渗透系数记为keq0.5，keq1.0，keq1.5，对总孔隙相同而孔隙尺寸不同时等效渗透系数两两对比，如表4所列。

表4 孔隙尺寸与等效渗透系数关系Tab.4 The relationship between pore size and equivalent permeability

由表4可看出：在孔隙率一定的情况下，等效渗透系数比值的平均值与相应的孔隙尺寸比值的平方(4，9，2.25)的绝对值最大误差为2.15%，即二者近似成正比，故水泥基材料的等效渗透系数与其孔隙尺寸的平方近似成正比，符合所应用的立方定律，亦符合松散颗粒状多孔介质其渗透率经验公式[32]，如式(4)，并且与文献[19]和[33]等人的研究结果十分相近，验证了本文所提出的数值模型与研究方法的合理性。

K=cd2

(4)

式中：K为渗透率，cm2；c为待定常数，与砂土性质有关；d为有效粒径，cm。

2.2 渗透系数与总有效孔隙率的关系

低渗透性水泥基材料的渗透性不仅与孔隙率有关，而且与孔隙的结构特征有关，只有连通的孔隙才能形成渗透通道。本文定义连通的孔隙为有效孔隙，非连通和盲端孔隙定义为死孔隙，其渗透系数取很小的值(实际分析中取1×10-12m/s)，为方便起见，将不同孔隙率的各级混凝土渗流分析模型记为模型尺寸L(n1/n2/n3/n4)下同。模型如图3所示，图3中深绿色为固体颗粒，深蓝色为非连通孔隙，浅色为连通孔隙。

图3 随机产生的有限元分析模型Fig.3 Random generation of FEA models

分析得到的等效渗透系数与总有效孔隙率关系如图4所示。由图4可以看出，渗透系数随有效孔隙率的增大而增大，经拟合成二次方关系，拟合方程如下：

当孔隙尺寸为0.5μm时，有：

R2=0.998

(5)

当孔隙尺寸为1.0μm时，有：

R2=0.999

(6)

当孔隙尺寸为1.5μm时，有：

R2=0.999

(7)

图4 水泥基材料等效渗透系数与总有效孔隙率的关系Fig.4 Relationship between equivalent permeability coefficient and total effective porosity of cement-based materials

该趋势与Christensen等人修正后的混凝土渗透率预测公式[12]，即Katz-Thompson方程式(8) 以及Song等[34]推导的混凝土渗透系数与总孔隙率的关系式(9) 是一致的。另外，许燕莲等[35]也通过试验的方法，测得多孔混凝土的有效孔隙率与其渗透系数是二次项关系，与本文得到的结果一致，进一步说明本文中模型与研究方法的有效性。

(8)

式中：lc为混凝土临界孔径，cm；φ为毛细孔隙率；φc为起渗透作用的毛细孔隙率临界值。

(9)

式中：k为渗透系数，m/s；C为常数；m为影响因子；B为与所选取的微孔隙结构模型有关。

3 孔隙率与连通性关系

有效孔隙(连通的孔隙)率与孔隙率之间存在密切关系，即孔隙率与连通性关系。将不同孔隙尺寸的各级水泥基材料渗流分析模型中，所有相同的相对孔隙率0.2，0.3，0.4，……，0.9与其所对应的相对有效孔隙率的关系列于表5。

由表5可知：相对有效孔隙率随着各级水泥基材料孔隙率的增大而增大，其值越来越趋近总孔隙率。当相对孔隙率小于0.2时，水泥基材料中的相对有效孔隙率等于0，即不存在连通的孔隙单元，这就解释了Katz-Thompson方程中临界孔隙率的存在，且本文所得结论与Garboczi等[10]的理论推导、Parrott[36]的试验研究所得出的结论是一致的。其中，Garboczi等基于逾渗理论计算指出，当混凝土的毛细孔率小于0.2±0.05时，所有的毛细孔均被胶凝孔阻隔，故只能利用层间的孔实现物质的相互交换，即毛细孔的临界孔径会降到胶凝孔，从而混凝土的渗透性降低；Parrott试验结果亦表明，当混凝土的毛细孔率小于0.2时，因孔隙不再连通，从而使得混凝土液态水入渗率将大幅降低。

表5 水泥基材料各级孔隙率与有效孔隙率统计关系Tab.5 Statistical relationship between porosity and effective porosity at all levels of cement-based materials

由上述分析可知：渗透性会随总孔隙增加而提高的根本原因是有效孔隙率的增大，水泥基材料中的毛细孔易形成连续的、相互贯通的网状结构体系，而这种连通的孔隙结构体系，成为了流体入渗与流动的主要通道；而当孔隙率含量较低时，孔隙之间的连通性变差，盲端孔隙在总孔隙中占有率高，从而导致水泥基材料的渗透性随之降低。

需要说明的是，水泥基材料中的孔隙尺寸一般从纳米级到微米级，本文所模拟的材料模型由不同孔隙率的微单元组成，最底层单元是真实孔隙，其渗透系数满足裂隙立方定律，其他层次单元由具有不同孔隙率微单元组成。当孔隙率较大时，微单元就可以代表一个孔隙，连通性由不同孔隙率的单元随机生成单元自然连接生成，这就很好地反映出了水泥基材料内部结构复杂的多尺度性、随机性，相比文献[21，34]和[35]等中的方法，本文提出的方法具有明显的优越性，亦减少了大量繁琐的试验。

4 结 论

从细观尺度着手，基于向上扩展多尺度法，应用蒙特卡罗方法随机生成了不同孔隙率的连续介质渗流分析模型，研究了低渗透性水泥基材料渗透性与其孔隙尺寸、孔隙率、等效孔隙率关系。

(1) 在孔隙率一定的情况下，等效渗透系数随其孔隙尺寸的增加而增大，并与孔隙尺寸的平方近似成正比。

(2) 在孔隙尺寸一定的情况下，等效渗透系数随着有效孔隙率的增加而增大，并与其成二次函数关系。

(3) 孔隙的连通性随着孔隙率的增大而增强，有效孔隙率随之提高，并趋近于总孔隙率；当孔隙率小于或等于0.2时，孔隙将不再连通，水泥基材料可视为不透水介质。今后需要进一步对分析模型产生时，等概率不同次数而引起的变异对其渗透性的影响。