基于像素预测和块标记的图像密文可逆信息隐藏

佘晓萌 杜 洋 马文静 殷赵霞

(多模态认知计算安徽省重点实验室(安徽大学) 合肥 230601)

(安徽大学计算机科学与技术学院 合肥 230601)

(e19301227@stu.ahu.edu.cn)

信息隐藏是一种将附加信息嵌入在指定载体中并能正确地提取信息的技术[1]，这种技术可以有效地保障信息安全性.在2020年中国商务部、科技部调整发布的《中国禁止出口限制出口技术目录》(商务部科技部公告2020年第38号)的公告中，“信息隐藏与发现技术”作为新增技术被列入其中，这直接证明了信息隐藏技术在安全领域的重要性.目前信息隐藏技术主要分为数字水印[2-3]、隐写术[4-5]以及可逆信息隐藏[6-7]3个分支.作为信息隐藏的分支之一，可逆信息隐藏技术不仅能正确地提取被嵌入的信息，还能无损地恢复原始载体.

基于数字图像的明文域可逆信息隐藏算法主要有2个常用的性能评价指标：一个是用来评价视觉质量的峰值信噪比；另一个是用来评价嵌入容量的嵌入率.近年来研究者们陆续提出许多明文域可逆信息隐藏算法[8-13]，并不断地提高算法的性能使其在现实生活中更具有应用价值.根据嵌入方式的不同，这些算法主要可以分为3类，分别是基于无损压缩[8-9]、基于直方图平移[10-11]和基于差值扩展[12-13]的算法.早期的明文域可逆信息隐藏算法主要通过第1类无损压缩的方法来预留空间，从而嵌入附加信息.第2类基于直方图平移的算法主要通过修改图像的像素直方图的峰值点和零值点之间的像素来嵌入信息.第3类基于差值扩展的算法则通过扩展2个像素之间的差值来实现信息隐藏.

随着云计算的发展和对隐私保护需求的日渐增长[14]，基于数字图像的密文可逆信息隐藏(reversible data hiding in encrypted images, RDHEI)技术的研究意义逐渐开始凸显[15].该技术将附加信息嵌入在加密图像中，最终不仅能正确地提取信息和无损地恢复原始图像，还能保障原始图像和附加信息的安全性.由于加密后的图像失去原始特征，所以不同于明文域可逆信息隐藏，在RDHEI算法中嵌入容量是其最主要的性能评价指标.在许多注重隐私保护的场景下，RDHEI技术都有较强的应用价值.比如在云环境下，原始图像在传输到云端之前往往需要进行加密，RDHEI可以完美地应用于此场景，在保护原始图像的同时也能保障信息安全性.此外，在一些医学、军事及法律等对隐私保护有特殊需求的领域中，RDHEI也有广泛的应用价值.

根据算法的不同阶段，RDHEI算法主要包含三方操作者：内容所有者、信息隐藏者和接收者.内容所有者是提供原始图像的一方，拥有加密密钥，能够对原始图像进行加密处理；信息隐藏者是嵌入附加信息的一方，拥有信息隐藏密钥，无法获取到原始图像的内容，仅可以在加密图像上嵌入附加信息从而生成标记加密图像；接收者则是接收最终的标记加密图像的一方，在同时拥有信息隐藏密钥与图像加密密钥时，可以正确地提取信息和无损地恢复原始图像.根据图像加密的顺序，目前已有的RDHEI算法主要被分为2类[15]：加密后留出空间(vacating room after encryption, VRAE)[16-30]和加密前预留空间(reserving room before encryption, RRBE)[31-44]的算法.如图1(a)所示，VRAE算法通过修改加密图像的像素以留出空间嵌入附加信息[16-30].由于加密图像的信息熵趋向于最大化，所以这类算法仅能实现较小的嵌入容量.近年来，在医疗领域，为了保护患者的隐私，医疗图像往往需要加密后进行传输，为了将患者的个人信息、诊断信息等附加信息嵌入到加密图像中，RDHEI算法对嵌入容量不断有更高的要求，由此RRBE算法逐渐得到了广泛的研究[31-44].图1(b)给出RRBE算法的框架图，这类算法通过分析原始图像的特征，利用原始像素的相关性来预留可嵌入的空间.相较于先前的VRAE算法，RRBE算法能够兼顾高嵌入容量、可逆性和安全性，本文主要研究的是这种算法.

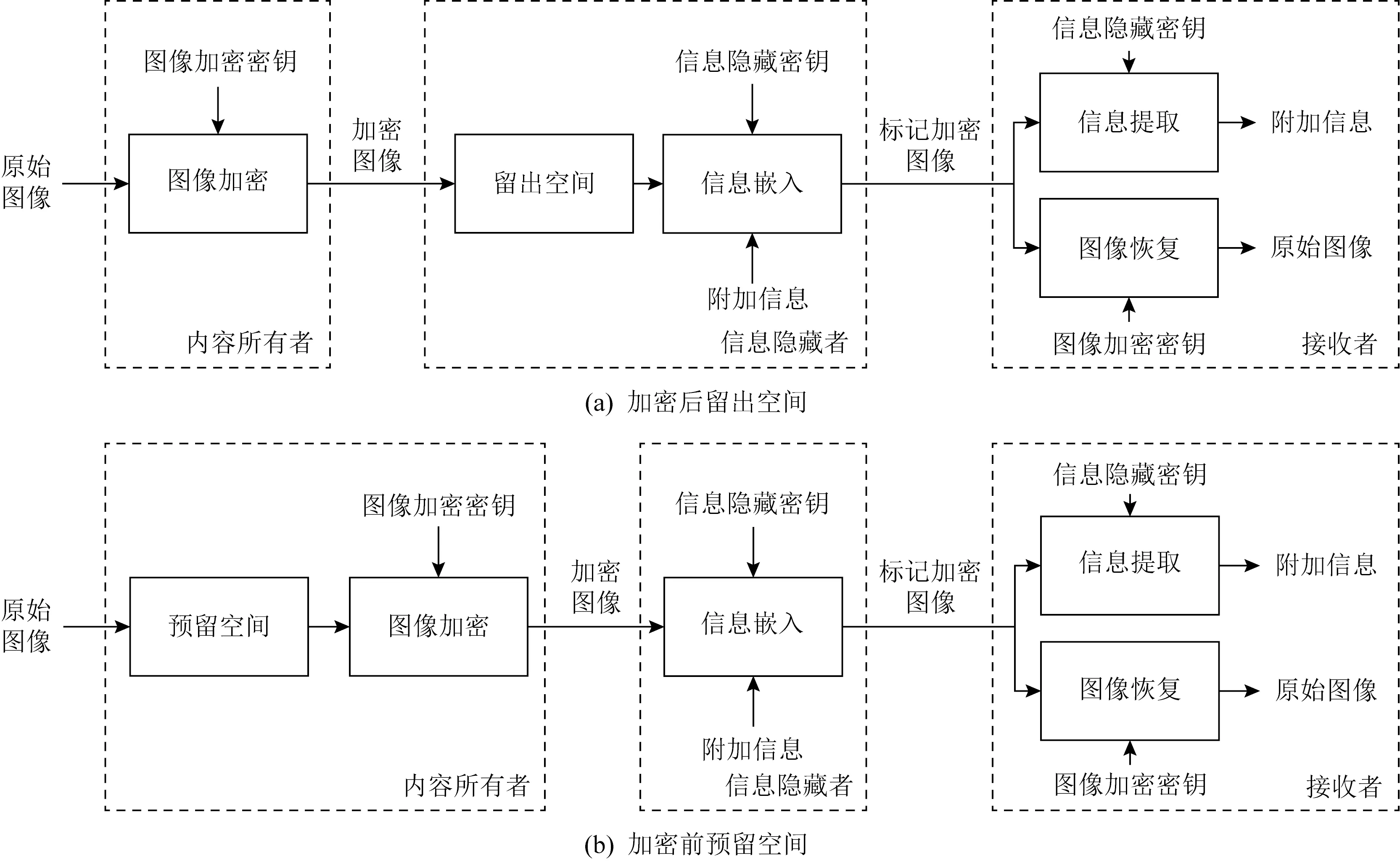
Fig. 1 Two categorized frameworks of RDHEI algorithms图1 RDHEI算法的2种框架图

文献[31]提出基于RRBE框架下的RDHEI算法，该算法的主要思想是通过选取原始图像一部分像素的最低有效位嵌入到另一部分像素中来预留空间，然后生成加密图像并嵌入附加信息.文献[32]使用流密码和块置乱的方法加密图像，嵌入信息的思想则与文献[31]类似.早期的算法多数是通过最低有效位替换来实现信息隐藏，很少有在最高有效位(most significant bit, MSB)上嵌入信息的算法，这是因为MSB替换会导致原始图像出现明显的失真.由于在RDHEI算法中加密后的图像已失去原始特征，所以无需和明文域可逆信息隐藏算法保持一致.文献[33]在图像的MSB上嵌入附加信息，相较于先前仅使用一部分的最低有效位来嵌入信息的算法，该算法在嵌入容量上具有非常明显的优势.尽管如此，该算法仍然存在一定的局限性，即仅利用MSB而无法利用其余的位.在该算法中辅助信息在未压缩的情况下被嵌入，会导致非法者仅通过分析辅助信息获取原始图像的内容[34].文献[35]设计了一种基于二值图像的RDHEI算法，该算法基于图像的空间相关性，通过保留预测像素的方式，在非预测像素的位置嵌入附加信息.文献[36]提出一种扩展游程编码和最高有效位平面重排列的方法，通过压缩最高有效位平面来留出空间嵌入附加信息.文献[37]通过二值块嵌入算法压缩图像的位平面，从而提升嵌入容量.文献[38]采用二叉树编码来标记像素以预留空间嵌入附加信息.文献[39]采用自适应像素排序的方法，构造2维预测误差直方图以嵌入信息.文献[40]设计一种双线性回归预测模型以提高图像像素的预测精度，进而提升算法的嵌入容量.文献[41]利用预测编码提出基于压缩感知渐进式恢复的RDHEI算法，在保证可逆性的同时实现了较高的嵌入容量.文献[42]提出一种自适应的多MSB预测的RDHEI算法，通过比较图像的多个有效位来自适应地嵌入信息，相较于文献[33]，此算法更进一步地提升了嵌入容量.文献[43]在文献[38]的基础上做出改进，更好地利用图像像素间的相关性以预留空间嵌入附加信息.文献[44]提出一种基于像素预测和位平面压缩的RDHEI算法，通过压缩预测误差位平面来留出空间.相较于先前的算法，该算法的性能更具有优势.

上述RDHEI算法都实现了较好的性能，但是无法同时实现高嵌入容量、完全可逆性和安全性.比如文献[33]中，原始内容的安全性无法得到保障.文献[42]实现了安全性，但此算法会产生过多的辅助信息，从而导致有效空间会被过多地占用，无法实现更高的嵌入容量.为保证安全性和完全可逆性的同时能实现更高的嵌入容量，本文提出一种基于像素预测和分块标记的RDHEI算法，主要贡献可总结为3个方面:

1) 提出了一种基于位平面分块特征的RDHEI算法，该算法可以充分利用位平面上的位置信息，成功地使用中值边缘预测器来计算预测误差.相较于原始图像位平面，计算后所得到的预测误差位平面上可嵌入的空间明显增多，得以进一步提升嵌入容量.

2) 自适应地标记了分块，使得标记分块所产生的辅助信息具有一定的稀疏特征，从而极大程度地被算术编码压缩.此外，对3种分块进行标记可以保证算法的完全可逆性.总体来说本算法不仅能同时保证算法的可逆性，还使得辅助信息占用的空间变少，有效空间能更充分地嵌入附加信息，以进一步地提升嵌入容量.

3) 先前的同类算法[35]需要保留分块的1 b作为预测值，而本算法能利用分块内的所有位置信息，从而提升RDHEI算法的性能.

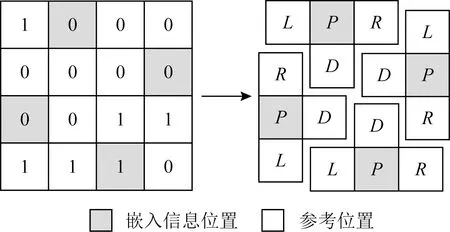
Fig. 2 An example of dividing a non-uniform block into four parts图2 举例将非统一块划分为4块

1 像素预测方案

像素预测方案是一种用于二值图像像素预测的方案[35].由于二值图像的像素取值只有2种可能性，且图像像素具有空间相关性，因此当前的像素值可通过其相邻像素值的预测结果而得.具体步骤是：先将一张未经处理的大小为M×N的二值图像划分为若干个不重叠的大小为k×k的像素块(本文k=4)；接着根据这些像素块的特征将其分为2类，每一类可使用相应的预测方案.本节将逐一介绍用于这2类像素块的像素预测方案.

第1类像素块为非统一块，其特点是块内的像素值不全相同.图2是将一个大小为4×4的非统一块划分为4个部分的例子，每部分由中心像素P及其相邻的3个像素L，R，D组成.根据像素相关性以及二值图像的像素取值只有2种可能(此处用0和1表示)的特性，可得到结论：当非统一块某一部分的中心像素P取值是0时，那么该像素的3个相邻像素L，R，D取值是0的概率更大，即这3个相邻像素值的和，大概率是0或者1；同理，当这部分中心像素值是1时，那么该像素的3个相邻像素值是1的概率会更大，即这3个相邻像素的和是2或者3的概率更大.

在算法过程中，当构成非统一块的4个部分都满足此条件时，即可根据相邻像素的取值，恢复被改变后的中心像素P的原始值.由此可得到用于非统一块的像素预测方案.

另一类像素块为统一块，块内像素值全为1或0.由于块内的像素值全部相同，因此仅根据当前块内的一个像素值，即可获取其余像素值.如图3所示是一个大小为4×4的统一块，可直观看到仅需保留每个统一块内像素R的值不变，即可成功地预测块内的其他像素值.

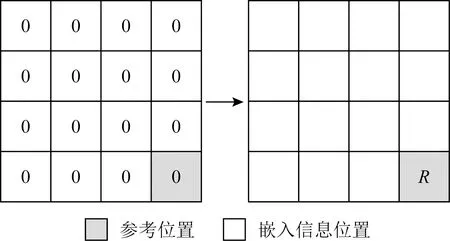
Fig. 3 A uniform block图3 统一块

2 本文算法

本文提出的基于像素预测和分块标记的RDHEI算法主要可以分为3个部分，具体框架如图4所示：第1部分由内容所有者提供原始图像，完成预处理和加密操作，以生成加密图像；第2部分由信息隐藏者在加密图像上完成附加信息嵌入操作，以生成标记加密图像；第3部分根据密钥的不同，由接收者完成提取信息和恢复图像的操作.

Fig. 4 The framework of the proposed algorithm图4 本文算法框架图

2.1 预处理

预处理阶段，主要对原始图像执行3部分操作：1)计算预测误差；2)生成预测误差位平面；3)分块标记.这3部分的具体操作在下文中逐一介绍.

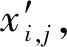
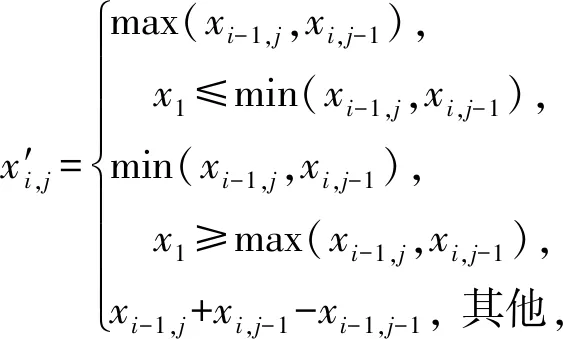
(1)

其中,1≤i≤M，1≤j≤N.此处将图像第1行和第1列的原始像素作为参考像素，不改变其像素值.接着根据xi,j的预测值，进一步计算得到其预测误差：

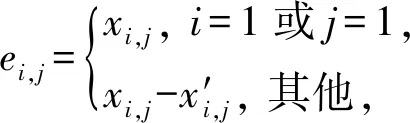
(2)

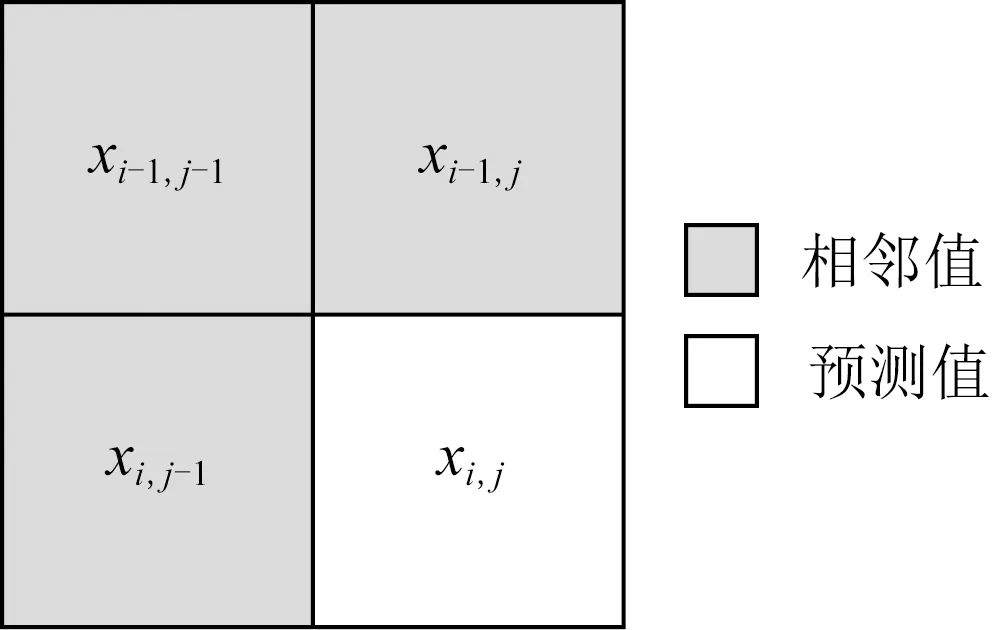
Fig. 5 The predicted value calculated by the median edge predictor图5 使用中值边缘预测器计算预测值

其中,1≤i≤M,1≤j≤N.由于后续需要置乱原始图像的像素位置，因此为保证算法的完全可逆性，采用一个有效位来表示预测误差值的符号位，其余有效位表示其数值位.具体步骤是先遍历图像的所有预测误差，将大于64和小于-64的预测误差定义为越界像素，并恢复其原始像素值.此处越界像素仅占极少一部分，所以算法过程中使用“1”标记越界像素，“0”标记其余像素，以生成一个大小为M×N且具有稀疏特征的标记图.基于此特征，可以用算术编码有效地无损压缩标记图，以减少空间占用.

2) 生成预测误差位平面.将除参考像素和越界像素以外的预测误差转换为8 b二进制序列：

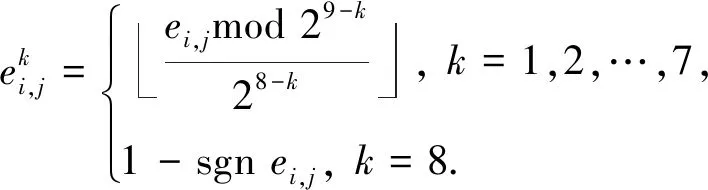
(3)

对参考像素和越界像素位置的预测误差进行转换：

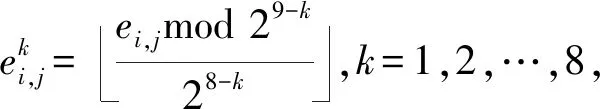
(4)

3) 分块标记.由于后续算法过程中需要置乱分块的初始位置，因此需使用标记图来记录初始位置以保证可逆性.为直观地描述分块标记过程，此处使用一个例子进行具体说明.图6是大小为M×N的预测误差位平面的一部分，该部分由4个分块组成，分别是值全为1的统一块B1、值全为0的统一块B0和非统一块B.按顺序遍历当前的位平面，分别记录B1的数量N1和B0的数量N0，并比较N1和N0的大小.由于图6中N1的值更大，所以此处用“00”标记B1，反之用“01”标记B0，最后用“10”标记B.由此可得到一个大小为(M/4)×(N/4)的稀疏序列，以及一个用来判断各个位平面中哪种统一块更多的二值序列.采用算术编码可以有效地压缩该序列，极大地减少空间占用.

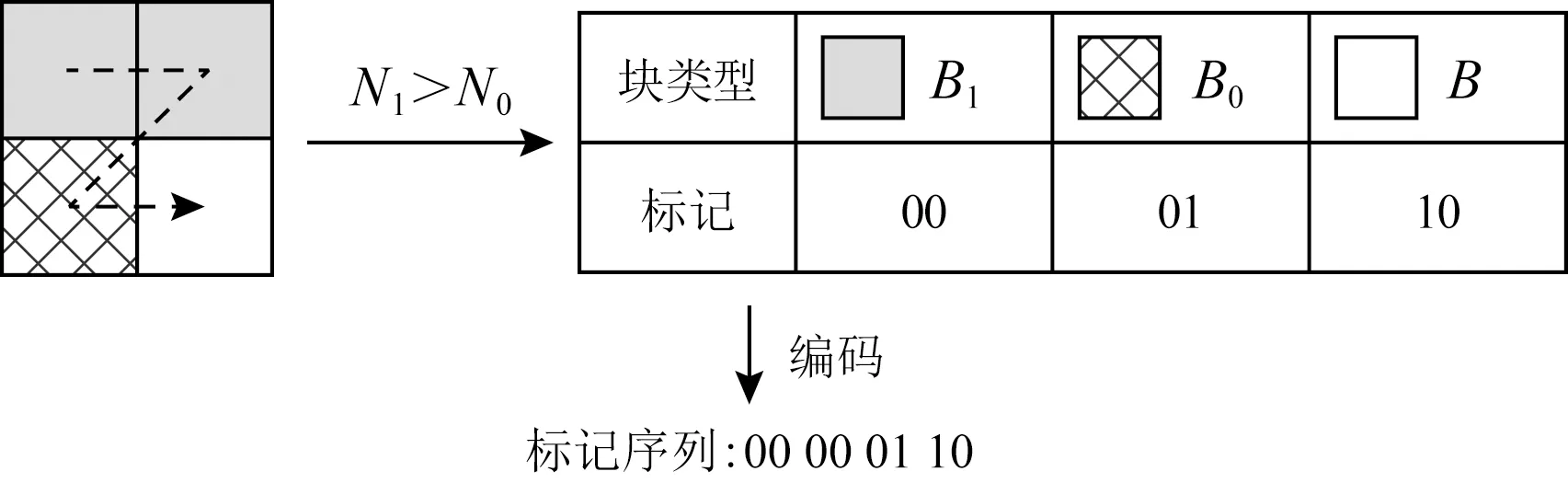
Fig. 6 An example of blocks labeling of bit planes图6 对位平面进行块标记的例子

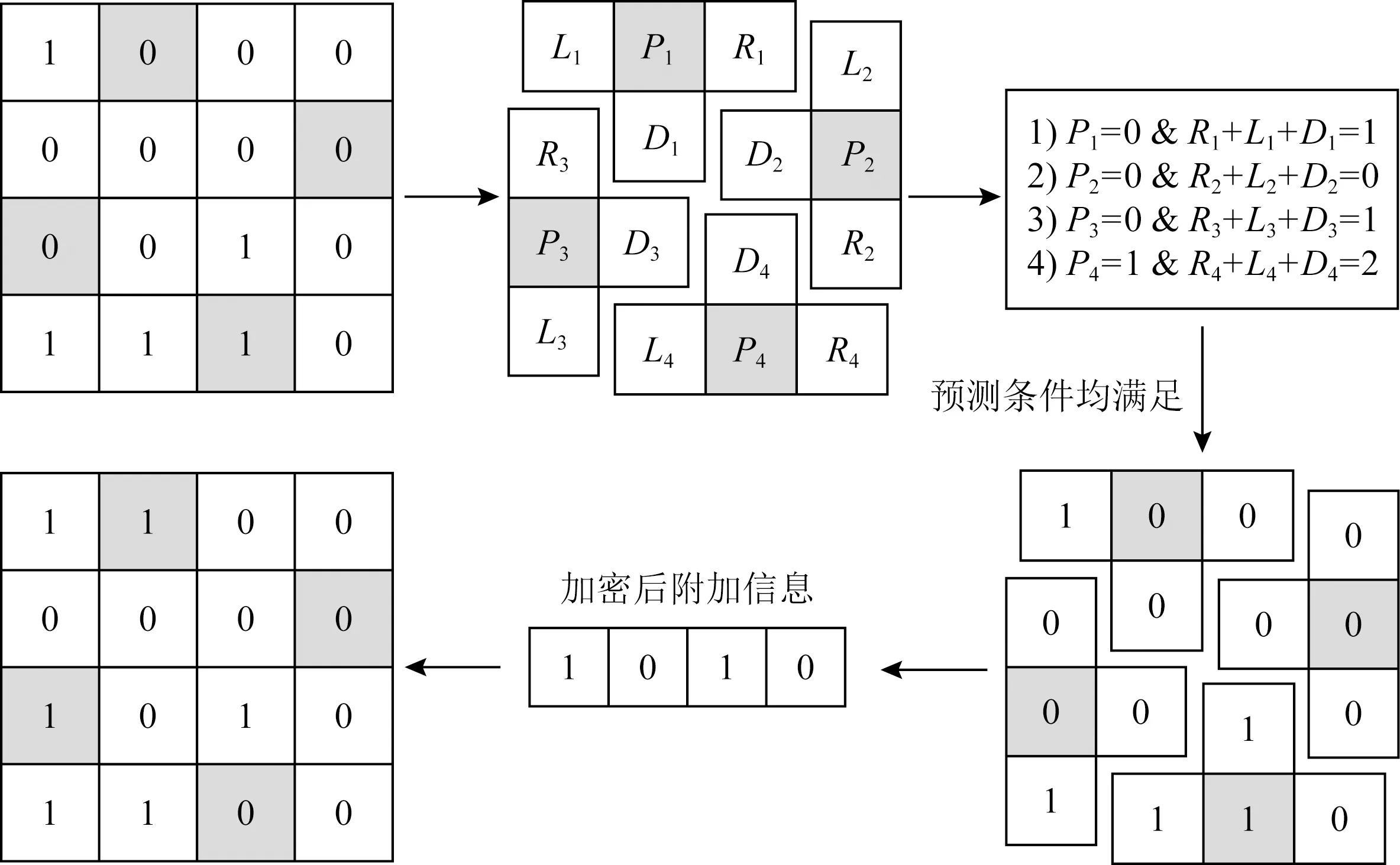
Fig. 7 An example of embedding data into a non-uniform block图7 在非统一块中嵌入信息的例子

遍历所有的非统一块，对于满足像素预测方案的非统一块，使用“0”标记表示可以嵌入信息，反之用“1”标记.此外，由于部分位平面的有效空间不足以容纳必要的辅助信息，故算法过程中用8 b二值序列来判断8个位平面是否能执行有效嵌入操作.最后重新排列有效位平面，将非统一依次排列在位平面的上方，统一块排列在下方，采用位替换的方法，将标记图等辅助信息嵌入到统一块中.

2.2 加密图像

预处理后，内容所有者对辅助信息以外的位置进行加密.使用密钥Ke生成一个大小为M×N的伪随机矩阵H，并将其转换为二进制序列：

(5)

对于第k个有效位平面的原始预测误差值，其加密后的值为

(6)

其中,1≤i≤M,1≤j≤N，⊕表示异或(XOR)操作.

2.3 嵌入信息

内容所有者将处理后的加密图像上传给信息隐藏者，由信息隐藏者执行嵌入操作.为提高本文算法的安全性，在执行嵌入操作前，使用信息隐藏密钥Kd对附加信息进行加密.下文给出嵌入信息的具体步骤：

1) 在非统一块中嵌入信息.如第1节所述，当非统一块的4个部分都满足预测条件时，则可以嵌入信息.因此，信息隐藏者仅需依次判断当前的非统一块是否为可嵌入块，然后采用位替换的方法嵌入附加信息即可.图7是在非统一块中嵌入信息的例子，每个块可分为4个部分，当且仅当4个部分都满足预测条件时，则可以在Pi(i=1，2，3，4)中嵌入信息.

2) 在统一块中嵌入信息.先前算法为保证可逆性，在统一块中嵌入附加信息前，需保留块内1 b原始值作为预测值[35].如此会导致块内的有效空间无法被合理利用，从而限制嵌入容量.为解决此问题，本文提出一种自适应标记分块的方法，即2.1节所介绍的标记方法.由于位平面上的3类分块已被标记，故本算法过程中无需保留块内1 b的原始值作为预测值.在统一块中嵌入信息的具体过程如图8所示，4个大小为4×4的非统一块B、统一块B1和B0组成位平面的一部分，其中B1和B0的全部位置都可用于嵌入附加信息.

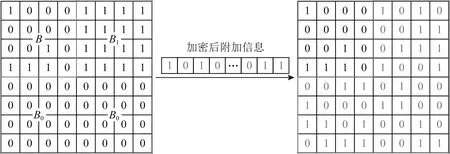
Fig. 8 An example of embedding data into a uniform block图8 在统一块中嵌入信息的例子

2.4 提取信息和恢复图像

由于在加密图像和嵌入信息阶段中，所用的密钥不同，所以根据相应的合法密钥，接收者可以完成相应的操作.

1) 接收者仅用信息隐藏密钥Kd，可以正确地提取附加信息.接收者将标记加密图像分为8个位平面，根据最高位平面右下角的辅助信息，依次判断当前位平面是否为可嵌入位平面，并定位附加信息位置.对于所有可嵌入的非统一块，按照嵌入阶段的逆过程来提取附加信息.对于所有的统一块中的附加信息，根据其位置依次提取全部的附加信息.最后使用密钥Kd依次解密，即可获得正确的附加信息.

2) 接收者仅用图像加密密钥Ke，可以无损地恢复图像.接收者使用加密密钥Ke解密图像，对于位平面中的非统一块，根据第1节提到的预测方案恢复嵌入位置的值；对于位平面中的统一块，根据所提取的标记图即可判断当前块的类型并恢复其原始值.最后，根据将各个位平面中所有重排列的块依次恢复至原位置，即可得到与原始图像一致的重构图像.

3) 接收者同时用信息隐藏密钥Kd和图像加密密钥Ke，则既可以正确地提取信息，也可以无损地恢复图像，具体操作与上述1)2)步骤类似.

3 实验结果与分析

为了验证算法的性能，从安全性、可逆性以及嵌入容量3个方面分析本文算法所实现的实验结果，并分别在BOSSbase[46]，BOWS-2[47]，UCID[48]这3个常用图像数据集上进行测试.

3.1 安全性

近年来RDHEI算法的安全性分析逐渐得到广泛关注[49]，为验证算法的安全性，以下将从视觉质量、直方图分布和像素改变率这3个方面进行详细分析.

1) 视觉质量.图9给出Lena图像的测试结果：图9(a)是原始Lena图像；图9(b)是由内容所有者传给信息隐藏者的加密图像；图9(c)是嵌入附加信息的加密图像，即标记加密图像；图9(d)是恢复的重构图像.原始图像与加密图像、标记加密图像之间的视觉差异越大，则表明算法安全性越好.通过人眼观察，可知原始图像图9(a)和加密图像图9(b)、标记加密图像图9(c)之间几乎不存在视觉相似性，由此从视觉质量的角度可知算法具有一定的安全性.

Fig. 9 Results of applying the proposed algorithm toLena image图9 将本文算法应用于Lena图像上的实验结果

2) 直方图分布.如图10所示，2幅灰度直方图分别展示出不同阶段的图像灰度值分布特征.图10(a)中原始图像直方图呈现出不规则的分布，其中包含原始图像的特征信息；而图10(b)中加密图像直方图的分布均匀而平缓，在其中难以获取像素间的规律，非法者通过分析加密图像难以获取原始图像的有效特征信息，这也证明了算法具有一定的强加密效果.

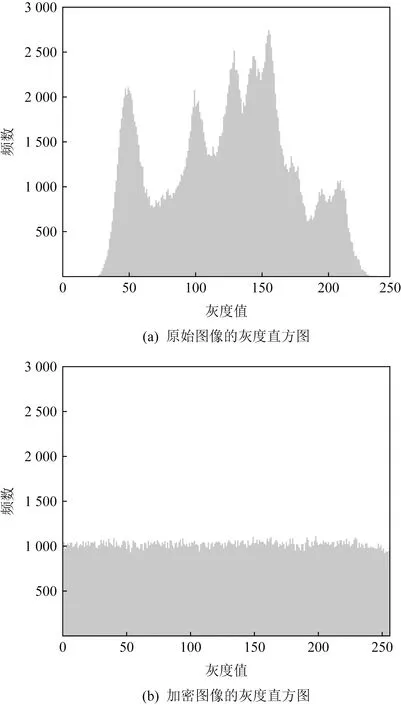
Fig. 10 Gray histograms of Lena image图10 Lena图像的灰度直方图

3) 像素改变率.本文算法不仅置乱了图像的原始位置，还使用伪随机生成器对图像进行加密.从理论角度证明算法的安全性，采用像素改变率的结果来证明加密图像与原始图像之间的差异，像素改变率越大，表明加密图像与原始图像之间的差异越大，则算法的安全性越高.像素改变率的计算步骤为：

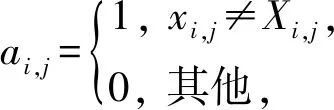
(7)

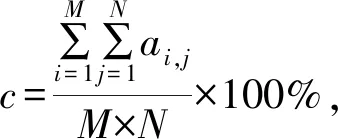
(8)

其中,1≤i≤M,1≤j≤N，c表示像素改变率，xi,j和Xi,j分别表示原始像素和加密像素，M和N分别表示图像的长和宽.实验结果表明，加密后图像的像素改变率非常高.比如，在几张常用的测试图像中，加密后原始图像的像素改变率皆为100%，即算法的安全性得到了保障.

3.2 可逆性

为验证算法中重构图像的质量，即可逆性，此处根据均方误差(mean square error, MSE)和结构相似性(structural similarity, SSIM)的值来判断重构图像与原始图像是否完全一致.重构图像的MSE越接近于0，SSIM越接近于1，则其失真程度越低.如表1所示，算法在3个常用图像数据集上的测试结果皆是MSE为0，SSIM为1，此结果表明重构图像与原始图像之间不存在失真，即两者完全一致.由此可知本文算法具有完全可逆性.

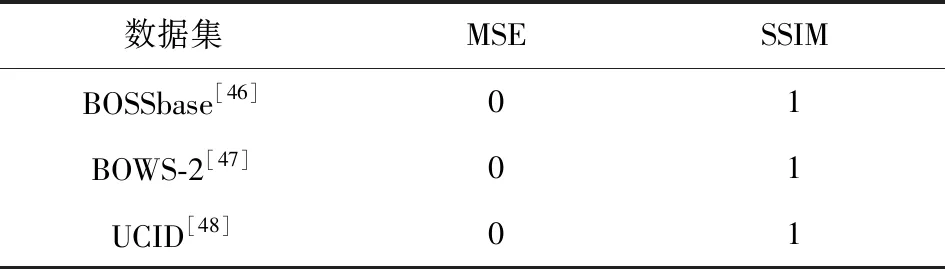
Table 1 Results of MSE and SSIM on Three Image Databases表1 3个图像数据集上MSE和SSIM的测试结果

3.3 嵌入容量

在实现安全性和可逆性后，嵌入容量的高低将决定RDHEI算法的现实应用价值，故嵌入容量常作为RDHEI算法的关键指标.图11给出在3个常用图像数据集上的嵌入容量的对比结果.

用每个像素可嵌入的比特数(bit per pixel, bpp)，即嵌入率的大小来衡量嵌入容量的高低.文献[33]采用位替换的方式，将信息嵌入到图像的MSB上.如图11所示，在3个常用数据集上使用文献[33]所提算法进行测试，所得到的嵌入率仅为0.966 bpp，0.968 bpp，0.893 bpp，而使用本文算法所得到的嵌入率分别是3.664 bpp，3.584 bpp，2.945 bpp.这是因为文献[33]所提算法未充分地利用图像的其他有效位.虽然在文献[42]中提出使用多个有效位来嵌入信息，但是这种算法产生的辅助信息没有被有效地压缩，因此辅助信息会占用较多的有效空间并导致嵌入容量变低.文献[43]利用像素间的相关性，采用二叉树编码来标记像素以进一步提升性能.文献[44]通过压缩图像的位平面，从而留出额外空间以嵌入附加信息.但从图11可直观看到，相较于RDHEI算法，本文的嵌入容量具有一定的优势.下文详细分析存在此优势的原因.

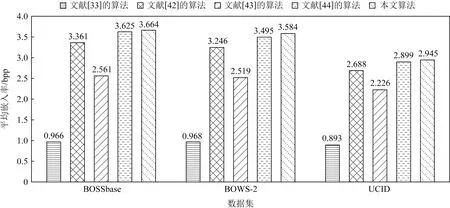
Fig. 11 Average embedding rate comparison in three databases图11 3个图像数据集上的平均嵌入率对比

1) 在预测误差位平面上嵌入信息.在本文算法中，采用中值预测器计算预测值.对于不同位置上的预测值，采用相应的方法计算预测误差，由此得到的预测误差位平面上有更多的可嵌入空间.如图12所示，相较于图10(a)中的原始像素直方图，预测误差直方图的分布范围更集中.本文算法能更好地利用图像冗余，这就意味着位平面上有更多相同的值组成统一块，从而嵌入更多信息.

Fig. 12 Histograms of the prediction errors图12 预测误差的分布直方图

2) 辅助信息不占用过多的有效空间.本文算法可以有效地压缩辅助信息，这使得位平面上有更多的空间用于嵌入附加信息，从而极大地提升嵌入容量.如2.1节所述，越界像素和总像素的标记图是本文算法的辅助信息之一.由于越界像素数量占总像素数量的比例非常低，故使用本文的标记方法所产生的辅助信息具有很明显的稀疏特征.例如，Lena图像的越界像素总数占总像素数的百分比仅为0.04%.基于此特征，辅助信息被压缩后仅占用很小的一部分空间.另一个主要的辅助信息是图像位平面分块的原始位置标记图.相较于原始像素，预测误差分布集中且数值较小，所以在大多数预测误差位平面上统一块的数量都大于非统一块的数量，此外本文算法使用“00”自适应地标记了数量较多的统一块.因此位置标记图也具有一定的稀疏特征，可以被算术编码有效地压缩.

3) 充分地利用像素块的空间.自适应地标记了位平面上的3类分块，根据标记图算法能实现可逆性.相较于已有算法，本文算法在统一块中嵌入信息前无需保留预测值，即块中的所有空间皆可用于嵌入信息.

4 总 结

本文提出了一种基于像素预测和分块标记的高容量RDHEI算法，在保障安全性和可逆性的同时，能实现更高的嵌入容量，使得算法更具有现实应用价值.比如RDHEI算法可被广泛地应用于医疗、军事和法律等领域.在医疗领域，为了保护患者的隐私，医疗图像往往需要加密后进行传输，为了将患者的个人信息、诊断信息等附加信息嵌入到加密图像中，RDHEI算法对嵌入容量不断有更高的要求.本文算法能更好地利用图像冗余，在预处理阶段，计算预测误差和分块标记的操作都使得图像中可嵌入空间变多.在图像加密阶段，有效的密钥使得算法的安全性得到保障.虽然理论分析和实验结果都表明本文算法在安全性、可逆性以及嵌入容量上有较优异的表现，但是在后续工作中我们还将继续改进算法的性能，设计更准确的预测方案来进一步提高算法的嵌入容量.

作者贡献声明：佘晓萌提出了算法思路和实验方案，完成实验并撰写论文；杜洋和殷赵霞对实验及论文写作提出指导性意见；马文静协助检查论文并提出修改意见.