含参模糊决策蕴涵

2022-09-06 02:03李德玉翟岩慧张少霞

计算机研究与发展 2022年9期

王琪李德玉,2 翟岩慧,2 张少霞

1(山西大学计算机与信息技术学院太原 030006)

2(计算智能与中文信息处理教育部重点实验室(山西大学) 太原 030006)

(chai_yanhui@163.com)

在哲学视角下，概念由外延和内涵2个部分组成,外延被定义为属于这个概念的所有对象的集合,而内涵则是所有这些对象所共有的特征(属性)集合.1982年，Wille等人[1]基于此提出了形式概念分析(formal concept analysis, FCA)理论.该理论根据概念之间的包含关系构成的概念格来反映数据的代数结构.近年来，FCA以其具有坚实的数学理论支撑、获取的知识层次清晰且逻辑性强等优点，逐渐吸引了广大研究者的兴趣[2-15].目前，FCA已经广泛应用于机器学习[2]、软件工程[3]、社会网络分析[4]、概念认知学习[5-6]、知识获取[7]和知识约简[8]等领域.

产生式规则是知识的主要表现形式，FCA对知识获取的研究就是对蕴涵的研究.由于获得的蕴涵数量庞大，无法满足用户的需求，因此如何获得完备的无冗余的蕴涵成为研究热点.Ganter等人[1]研究了蕴涵的语义特征和语构特征，并且给出一种在所有蕴涵基中蕴涵个数最少的蕴涵基，称为自然基.文献[16]进一步从逻辑角度出发，提出了一种用于判别蕴涵集是否为完备集的充要条件，并且给出一种生成蕴涵完备集的算法.

为了进一步减少蕴涵的数目，Qu等人通过限制蕴涵的前件和后件分别为条件属性和决策属性提出了决策蕴涵的概念[17]，并完整讨论了决策蕴涵的逻辑特征[18].基于决策蕴涵的逻辑研究，文献[19]提出了决策前提的概念，并据此生成一种完备无冗余且最优的知识基：决策蕴涵规范基.文献[20]对决策蕴涵与粒规则[21]和概念规则[22]进行了比较研究，发现与决策蕴涵相比，粒规则和概念规则存在信息损失.另外，文献[23]也从逻辑角度研究了具有支持度和可信度的决策蕴涵.文献[24]将决策蕴涵拓展到模糊形式背景上，提出了模糊决策蕴涵的概念，并讨论其语义特征和语构特征.文献[25]提出模糊决策蕴涵规范基的概念，并证明模糊决策蕴涵规范基的完全性、无冗余性和最优性.

模糊决策蕴涵可以基于语气真值算子(hedge)进行简化知识[24-25]，但并没有考虑阈值这一参数化策略.在现实生活中，阈值在简化知识方面具有重要的作用.例如，在知识“如果1个女性年轻的程度超过0.8，那么该用户喜欢爱情喜剧类电影的程度将会超过0.5”中，0.8和0.5均为阈值，但模糊决策蕴涵理论并不适用挖掘此类具有阈值的知识.事实上，模糊决策蕴涵理论只能挖掘诸如“年轻女性喜欢爱情喜剧类电影”不带有阈值的知识，其中年轻和爱情喜剧类均为模糊集.可以发现，模糊决策蕴涵仅仅是阈值为1时的特例，因此，研究含有阈值的模糊决策蕴涵不仅具有应用意义，而且具有理论意义，即含有阈值的模糊决策蕴涵是模糊决策蕴涵的扩展理论.

本文对模糊决策蕴涵进行拓展，定义了含参模糊决策蕴涵，并研究了其语义特征和语构特征.

1 模糊逻辑

本节简要介绍相关的基础背景知识.

定义1[26].在Pavelka逻辑中，真值结构是形如(L,∧,∨,⊗,→,0,1)的完备剩余格，满足3个性质：

1) (L,∧,∨,0,1)是以0和1为最小元和最大元的完备格；

2) (L,⊗,1)为交换幺半群，即⊗满足交换律和结合律，且有∀a∈L,a⊗1=1⊗a=a；

3) ⊗，→为伴随对，满足伴随条件a⊗b≤c当且仅当a≤b→c，其中a,b,c∈L.

运算⊗，→分别表示模糊合取和模糊蕴含，L中的元素称为真实度.

常见的完备剩余格的例子是单位区间[0,1]，∧和∨运算分别是最小值和最大值.3个单位区间上重要的伴随对如下.

a⊗b=max(a+b-1,0)，
a→b=min(1-a+b,1).

Godel：

Goguen：

a⊗b=a·b，

语气真值算子(hedge)可以增加推理的灵活性.

定义2[24].模糊集L上的语气真值算子定义为映射*:L→L，满足：

1) 1*=1,a*≤a，

2) (a→b)*≤a*→b*，

3)a**=a*，

其中，a,b∈L.

最大的语气真值算子为Identity，即对任意的a∈L，都有a*=a.

最小的语气真值算子为Globalization，即

性质1[24].完备剩余格主要具有10条性质.对于a,b,c,yi∈L：

1)a≤b⟺a→b=1；

2)a≤b→c⟺b≤a→c；

3) (a⊗b)→c=(a→(b→c))；

4)a→∧yi=∧(a→yi)；

5) 1→a=a；

6)a⊗(a→b)≤b；

7)a≤(b→(a⊗b))；

8)a*⊗b*=(a⊗b)*；

9)a≤(b→(a⊗b))*；

10)a⊗∨yi=∨(a⊗yi).

定义3[24].模糊集A是定义在论域X上的一个映射，它赋予每个x∈X一个隶属度A(x)∈L.论域X上的所有模糊集记为LX.

定义4[24].L-模糊集之间的包含关系定义为

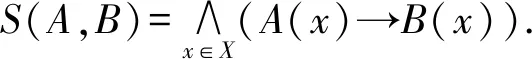
性质2[24].模糊集之间的包含关系主要有4个性质：

1)a→S(A,B)=S(a⊗A,B)=S(A,a→B)；

2)S(A∪B,C)=S(A,C)∧S(B,C)；

3)S(A,B∩C)=S(A,B)∧S(A,C)；

4)S(A,B)⊗S(B,C)≤S(A,C).

2 含参模糊决策蕴涵的语义、语构及其性质

类似于模糊决策蕴涵[24]，含参模糊决策蕴涵的研究内容包括语义和语构2个方面.

1) 语义方面的研究包括：①含参模糊决策蕴涵的合理性，即含参模糊决策蕴涵是否合法；②含参模糊决策蕴涵的无冗余性，即含参模糊决策蕴涵能否被其他含参模糊决策蕴涵导出；③含参模糊决策蕴涵的完备性，即含参模糊决策蕴涵是否包含完整的信息.

2) 语构方面的研究包括：①推理规则的合理性，即含参模糊决策蕴涵能否使用推理规则得出；②推理规则的完备性，即是否能用这些推理规则推出所有可能的含参模糊决策蕴涵.

2.1 含参模糊决策蕴涵的语义特征

本文使用Bělohlávek等人[14]提出的同时考虑阈值和语气真值算子的概念构成算子，并将其引入到模糊决策蕴涵中.

定义5.C∪D上的含参模糊决策蕴涵为公式A⟹B，其中A∈LC，B∈LD分别是条件属性和决策属性的模糊集.设模糊属性集T∈LC∪D，TC={t/l∈T|t∈T∩C}，TD={t/l∈T|t∈T∩D}，则其对含参模糊决策蕴涵A⟹B的满足程度定义为

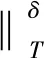
其中,δ=(δ1,δ2)∈L×L，δ1和δ2是2个阈值参数.

例1.令L={0,0.25,0.5,0.75,1}，C={s,l}，D={f,n}，δ1=δ2=0.5，使用ukasiewicz伴随对和Identity语气真值算子，令

A⟹B={0.5/s,0.5/l}⟹{0.5/f,0.5/n}，
T={0.75/s,0/l,0.25/f,0.5/n}，
TC={0.75/s,0/l}，
TD={0.25/f,0.5/n}，

则

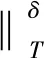
这表明数据T满足含参模糊决策蕴涵“若对象含有属性s和l的程度均超过0.5，则其含有属性f和n的程度也均超过0.5”的程度为1.

定理1.设模糊属性集T∈LC×LD，含参模糊决策蕴涵为A⟹B，A∈LC，B∈LD，则有

证明.由定义5及伴随对的性质容易证明该结论成立.

证毕.

定理1的第1个等式表明，在阈值δ=(δ1,δ2)下，数据T满足含参模糊决策蕴涵的程度与(δ1→TC)∪(δ2→TD)满足模糊决策蕴涵的程度相同.定理1的第2个等式表明，数据T满足含参模糊决策蕴涵的程度等于数据T满足前件为δ1⊗A、后件为B的模糊决策蕴涵的程度超过δ2的程度.

定理2.设模糊属性集T∈LC∪D，则对含参模糊决策蕴涵A⟹B，A∈LC，B∈LD有

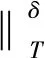
证明.由定理1以及文献[22]中定理1的证明可证.

证毕.

定义6.T={T1,T2,…,Tn}⊆LC∪D满足含参模糊决策蕴涵A⟹B，A∈LC，B∈LD的程度定义为

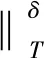
定义6表明，含参模糊决策蕴涵在数据集T中成立的程度是其在所有数据中Ti∈T成立程度的最小值.

定义7.设L为含参模糊决策蕴涵集，L的所有模型定义为

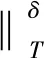
其中,L(A⟹B)是A⟹B属于L的程度.含参模糊决策蕴涵从L中语义导出的程度定义为

即A⟹B从L导出的程度等于L的全部模型满足A⟹B的程度.

例2.令含参模糊决策蕴涵集L为

L={({0.5/s,0.25/l}⟹{0.25/f,0.5/n})/0.75,
({0/s,0.5/l}⟹{0.5/f,0/n})/0.75}，

令δ1=δ2=0.5.对于T={0.5/s,0/l,0/f,0.5/n}，使用ukasiewicz伴随对和Identity语气真值算子计算可得

可以发现，T满足L中含参模糊决策蕴涵的程度均为1，从而T是L的模型.

定理3.对于含参模糊决策蕴涵集L和含参模糊决策蕴涵A⟹B，A∈LC，B∈LD有

1)Modδ(L)={T|(δ1→TC)∪(δ2→TD)∈Mod1(L)}；

证明.类似于文献[22]可证.

证毕.

定理3的1)和2)相当于定理1的第1个等式的推论，定理3的3)是2)的推论.值得注意的是，由定理3的2)并不能得出含参模糊决策蕴涵的语义导出程度关于参数δ是递减的，只能得出该语义导出程度的2个极值.参数的引入，使得语义导出程度的变化更加复杂，不再是单纯的单调.

给定一个条件属性模糊集以及参数δ1和δ2，该条件属性模糊集可以从给定的含参模糊决策蕴涵集中得出的所有结论，即该条件属性模糊集的闭包.

定义9.对于含参模糊决策蕴涵集L和A∈LC，定义A相对于L的闭包为

例3.设A={0.5/s,0/l}，δ1=δ2=0.5，使用ukasiewicz伴随对和Identity语气真值算子.令

L={(A1⟹B1)/0.75,(A2⟹B2)/0.75}=
{({0.5/s,0.25/l}⟹{0.25/f,0.5/n})/0.75,
({0/s,0.5/l}⟹{0.5/f,0/n})/0.75}，

则

L(A1⟹B1)⊗S(δ1⊗A1,A)*⊗B1=
0.75⊗1⊗B1={0/f,0.25/n}，
L(A2⟹B2)⊗S(δ1⊗A2,A)*⊗B2={0/f,0/n}.

对于不在模糊决策蕴涵集中的模糊决策蕴涵，有

L(A1⟹B1)⊗S(δ1⊗A1,A)*⊗B1=
0⊗S(δ1⊗A1,A)*⊗B1={0/f,0/n}，

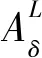
证明.对于任意的A1⟹B1∈L，记

c=L(A1⟹B1)⊗S(δ1⊗A1,A)*，

显然有

(c⊗B1(u)⊗δ2)→(c⊗B1(u)⊗δ2)=1.

由性质1的结论3)和4)有

(c⊗B1⊗δ2)→(c⊗B1⊗δ2)=
c→S(δ2⊗B1,δ2⊗c⊗B1)=1，

从而c≤S(δ2⊗B1,δ2⊗c⊗B1)，即

L(A1⟹B1)⊗S(δ1⊗A1,A)*≤
S(δ2⊗B1,δ2⊗L(A1⟹B1)⊗
S(δ1⊗A1,A)*⊗B1).

又因为

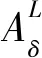
从而可得

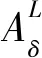
即

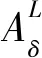
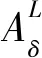
证毕.

例4.(续例3)令A={0.5/s,0/l}，由例3可得

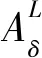
对于L中的含参模糊决策蕴涵有

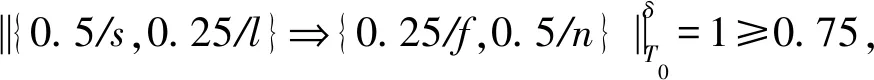
因此有T0∈Modδ(L).

证毕.

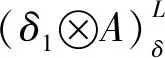
证明.对于任意的T∈Modδ(L)和A1⟹B1有

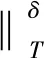
由伴随对的性质有

L(A1⟹B1)⊗S(δ1⊗A1,TC)*≤
S(δ2⊗B1,TD)⟺L(A1⟹B1)⊗
S(δ1⊗A1,TC)*→
S(δ2⊗B1,TD)=1.

由性质1的结论8)和性质2的结论4)有

S(δ1⊗A1,δ1⊗A)*⊗
S(δ1⊗A,TC)*≤S(δ1⊗A1,TC)*，

两边同乘L(A1⟹B1)可得

L(A1⟹B1)⊗S(δ1⊗A1,δ1⊗A)*⊗S(δ1⊗
A,TC)*≤L(A1⟹B1)⊗S(δ1⊗A1,TD)*，

由→的性质有

L(A1⟹B1)⊗S(δ1⊗A1,δ1⊗A)*⊗
S(δ1⊗A,TC)*→S(δ2⊗B1,TD)≥
L(A1⟹B1)⊗S(δ1⊗A1,TC)*→
S(δ2⊗B1,TD)=1，

从而

L(A1⟹B1)⊗S(δ1⊗A1,δ1⊗A)*⊗
S(δ1⊗A,TC)*≤S(δ2⊗B1,TD)，

由性质1的结论3)有

S(δ1⊗A,TC)*≤L(A1⟹B1)⊗
S(δ1⊗A1,δ1⊗A)*→
S(B1,δ2→TD)=
S(δ2⊗L(A1⟹B1)⊗
S(δ1⊗A1,δ1⊗A)*⊗B1,TD)，

由性质2的2)和性质1的4)，上式等价于

由定义9可得

从而

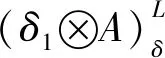
即

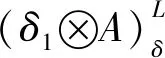
证毕.

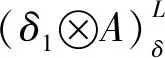
定理6.对于含参模糊决策蕴涵集L，可得

证明.由定理4容易得

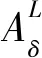
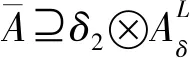
进而

反过来，设T∈Modδ(L)，有

L(A1⟹B1)≤S(δ1⊗A1,TC)*→
S(δ2⊗B1,TD)⟺L(A1⟹B1)⊗
S(δ1⊗A1,TC)*≤S(δ2⊗B1,TD)⟺
L(A1⟹B1)⊗S(δ1⊗A1,TC)*≤
δ2⊗B1(d)→TD(d),∀d∈D
⟺L(A1⟹B1)⊗S(δ1⊗A1,TC)*⊗
δ2⊗B1(d)≤TD(d),∀d∈D⟺
L(A1⟹B1)⊗S(δ1⊗A1,TC)*⊗
δ2⊗B1⊆TD，

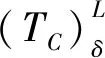
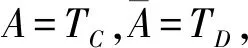
证毕.

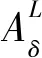
例5.设C={a}，D={z}，真值结构采用L={0,0.25,0.5,0.75,1}，δ1=0.75，δ2=1，采用ukasiewicz算子和Identity语气真值算子.设含参模糊决策蕴涵集为L={{1/a}⟹{1/z}/1}.计算闭包及其模型如表1所示：

Table 1 Closure and Models表1 闭包及其模型

因此有

Modδ(L)={{0/a,0.25/z},{0/a,0.5/z},
{0/a,0.75/z},{0/a,1.0/z},{0.25/a,0.75/z},
{0.25/a,1/z},{0.5/a,0.75/z},{0.5/a,1/z},
{0.75/a,0.75/z},{0.75/a,1/z},{1/a,1/z}}.

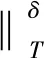
定理7.对于含参模糊决策蕴涵集L和含参模糊决策蕴涵A⟹B，有

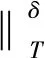
另一方面，设T∈Modδ(L)，由定理5有

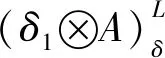
即

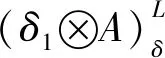
因此

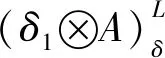
从而由性质2的结论4)可知

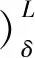
因此

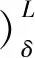
等价于

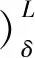
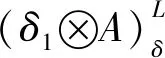
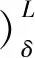
证毕.

定理7同时也给出了含参模糊决策蕴涵从含参模糊决策蕴涵集中导出程度的计算方法.

2.2 含参模糊决策蕴涵的语构特征

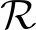
其中φ1,φ2,…,φn,φ是n+1条含参模糊决策蕴涵，a1,a2,…,an,a∈L，ai可以为L(φi)，即φi的隶属度，也可以为使用推理规则从含参模糊决策蕴涵集推导的φi的程度.

推理规则的含义为：若含参模糊决策蕴涵φi具有隶属度或者导出程度ai，i∈{1,2,…,n}，则可推导出程度为a的含参模糊决策蕴涵φ.

针对含参模糊决策蕴涵，本文提出3条推理规则.

1) 含参模糊变换推理规则：

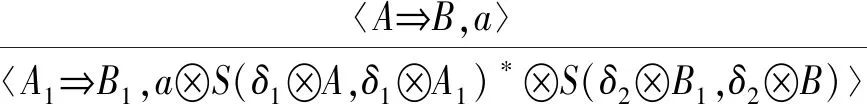
2) 含参模糊扩增推理规则：

3) 含参模糊转换推理规则：

定义10[24].模糊推理规则

是合理的，若

Mod({a1/φ1,a2/φ2,…,an/φn})=
Mod({a1/φ1,a2/φ2,…,an/φn,a/φ}).

定理8.上述3条规则是合理的.

证明.含参模糊变换推理规则：设T是A⟹B,a的模型，即‖A⟹B≥a，要证明T也是A1⟹B1,a⊗S(δ1⊗A,δ1⊗A1)*⊗S(δ2⊗B1,δ2⊗B)的模型，即证

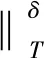
这等价于证明

a⊗S(δ1⊗A,δ1⊗A1)*⊗S(δ2⊗B1,δ2⊗B)⊗
S(δ1⊗A1,TC)*≤S(δ2⊗B1,TD)，

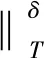
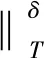
由性质2的结论4)可得

S(δ2⊗B1,δ2⊗B)⊗S(δ2⊗B,TD)≤
S(δ2⊗B1,TD)，

(1)

另外，由性质1的结论6)有

(S(δ1⊗A,TC)*→S(δ2⊗B,TD))⊗
S(δ1⊗A,TC)*≤S(δ2⊗B,TD)，

(2)

联立式(1)和式(2)可得

(S(δ1⊗A,TC)*→S(δ2⊗B,TD))⊗
S(δ1⊗A,TC)*⊗S(δ2⊗B1,δ2⊗B)≤
S(δ2⊗B,TD)⊗S(δ2⊗B1,δ2⊗B)≤
S(δ2⊗B1,TD)，

上式可变形为

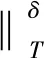
另外，由性质1的结论6)又有

S(δ1⊗A,δ1⊗A1)*⊗S(δ1⊗A1,TC)*≤
S(δ1⊗A,TC)*，

因此可得

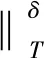
即有

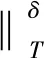
这说明T也是A1⟹B1,a⊗S(δ1⊗A,δ1⊗A1)*⊗S(δ2⊗B1,δ2⊗B)的模型.

证毕.

含参模糊扩增推理规则和含参模糊变换推理规则的合理性证明类似.

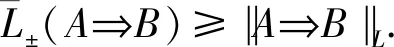
定理9.上述3条模糊推理规则相对于含参模糊决策蕴涵的语义特征是完备的.

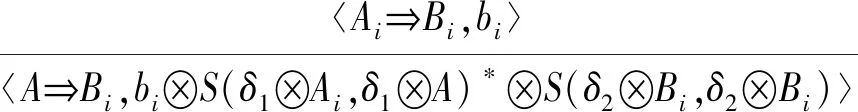
其中bi=L(Ai⟹Bi).由含参模糊转换推理规则有

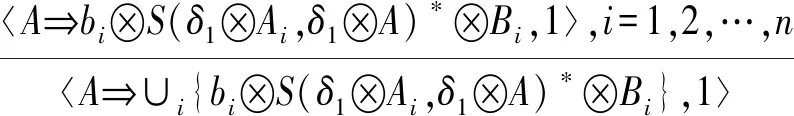
再由含参模糊扩增推理规则合并得到的所有含参模糊决策蕴涵可得

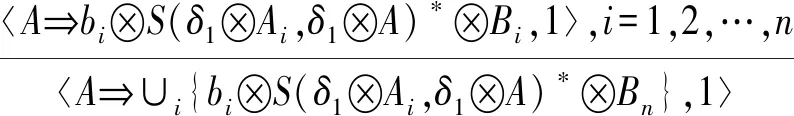
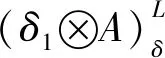
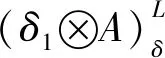
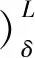
证毕.

3 结论

本文在模糊决策蕴涵中引入了阈值，提出了含参模糊决策蕴涵，提升了模糊决策蕴涵的可调节性和应用价值.在语义方面，研究了含参模糊决策蕴涵的模型和语义导出程度的计算方法；在语构方面，将模糊决策蕴涵中的3条推理规则拓展到含参模糊决策蕴涵，并证明了这些推理规则的合理性和完备性.

从理论上看，将阈值引入模糊决策蕴涵的意义并不局限于构建一种以模糊决策蕴涵为特例的理论框架.一方面，这种引入方式具有普遍意义，事实上，定义4和性质1的1)正是模糊集包含度和含参的模糊集包含度的定义.因此，这个引入方式对整个粒计算领域均有参考意义.另一方面，由定义5可以看出，将阈值引入模糊决策蕴涵本质上相当于在完备剩余格上建立一种协调结构，而定理1正是说明这种协调结构所具有的特性，因此，本文的结论对完备剩余的公理化或代数研究也具有一定的启发意义.进一步来说，含参模糊决策蕴涵同时包含阈值和语气真值算子2种知识简化策略，但本文并没有考虑这种简化策略之间的联系和相互作用.事实上，如果说参数的引入是在完备剩余格上建立一种协调结构，那么语气真值算子就是完备剩余格上的另一种协调结构，因此，从代数角度和应用角度研究这2种结构之间的关系将是下一步的研究工作.

值得指出的是，在应用中，用户可能需要根据不同的实际需求选择合适的阈值.由定理1可知，给定模糊决策背景，参数δ1越小或参数δ2越大，满足含参模糊决策蕴涵的模型也越少，因此模糊决策背景中成立的含参模糊决策蕴涵也越少.当δ1和δ2分别为0和1时，用户可以得到最严格意义上的模糊决策蕴涵；用户可以进一步增加δ1或减小δ2来获取更多的模糊决策蕴涵.在具体应用中，用户可以参考专家的意见来选定阈值，或选取一些指标(如分类性能等)来有监督地选择合适的阈值.