设计思维可视化作业 提升数学建模素养

江苏省无锡市堰桥高级中学 胡谢芳

《普通高中数学课程标准（2017年版2020年修订）》（下文简称“《课标》”）指出，数学建模是对现实问题进行数学抽象，用数学语言表达问题、用数学方法构建模型解决问题的素养；是将实际问题数学化，用数学思想、方法和知识来解决实际问题的过程，是数学应用的重要形式。数学建模过程主要包括：在实际情境中从数学的视角发现问题、提出问题，分析问题、建立模型，确定参数、计算求解，检验结果、改进模型，最终解决实际问题。

数学建模和一般数学题的解法是不一样的，我们讲数学建模实际上是情境化命题的方式。学生对情境化命题的解答易有畏惧心理，随着高考新方案的实施，情境化命题的题型也更多样化，这无形中给学生带来更多的挑战。因此，笔者认为，在日常教学中应引导学生灵活运用数学方法，设置可视化作业，提升学生数学建模的素养。

一、可视化定向锤炼解题思路

（一）基于简单建模阶段的可视化作业

随着新方案的实施，高考题型已经有四大类：单项选择，多项选择，填空和解答题。笔者认为，平时作业的设置应注意小题解题思维的可视化。

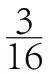
在日常教学中，对于这类实际问题，学生很容易分辨属于数学概率问题。若在平时作业中，笔者会要求学生将分析过程用思维导图标注出来。

这属于简单建模阶段的情境问题，学生可以直接套用基本数学模型，利用思维导图可以帮助学生分析问题，厘清思路，从而直接借助或引用数学知识解决实际问题。

（二）基于基本典型建模阶段的可视化作业

这一阶段对学生的要求相对提高，需要学生在熟悉的情境中发现问题并将其转化为数学问题；能够选择合适的数学模型来解决实际问题，而这一类数学模型通常是我们熟悉的基本函数模型。这就要求我们在日常教学中，要引导学生对一些基本数学模型进行一一归纳。例如，指数函数、对数函数、幂函数和数列模型可以解决增长率、利率等问题；函数、不等式模型可以解决最值问题；二次曲线、圆锥曲线等模型可以解决卫星轨迹、拱桥等与轨迹相关的问题。因此，该阶段的作业设置，需要学生明确解决何种问题，大概需要哪种基本的数学模型。

如：某公司一年购买某种货物600吨，每次购买x吨，运费为6万元/次，一年的总存储费用为4x万元，要使一年的总运费与总存储之和最小，则x的值是____。

此题学生可以明确与不等式、函数有关，因此需要建立数量关系。作业中学生若将思维过程体现出来，也可提升正确率。

作业的思维导图可以更好地帮助学生从实际问题出发，运用合适的数学模型、明确的数学知识解决问题。

因此，当分配因子λ1、λ2、λ3满足上述条件时，相比分散决策下各决策主体的利润，集体决策下经过协调后的制造商、零售商、物流服务集成商以及物流服务提供商的利润均实现了帕累托改进，同时产品供应链的利润与物流服务供应链的利润也实现了帕累托改进。

以上两个阶段的要求，相当于《课标》中的数学建模水平一，在高考命题中，更有可能出现在小题中，小题重结果。因此，在平时的作业中强化解题思路，对于处理综合型数学建模问题，可以起到夯实基础的作用。

二、可视化定向锤炼拓展解题技能

在《课标》说明下，笔者以为综合建模是高考命题的重点，对学生的综合能力要求较高，能够在综合情境下，运用数学思维进行分析，把模糊的问题提炼成比较明确的数学问题，运用数学建模的一般方法和相关知识解决问题，在解题过程中，将复杂问题逐一破解，最终建立数学模型，解决问题。因此，在日常的教学中，除了课堂上要充分体现分析过程、解题思路外，作业中也要充分要求学生表现出数学思维，能用流畅的数学方式展示分析过程。

这一题体现了情境问题最大的特征，就是题目很长，很烦琐。学生读完题目，还是一头雾水。那么，做作业时笔者会要求学生进行对题目的剥离，把情境问题逐渐数学化。对剥离后的问题再次进行分析，逐渐厘清数量关系，第（1）小题思维过程体现如下：

有了这样的一个简单分析，学生也会正确的建立不等关系，解决预设的情境问题。

对于第（2）小题的解答，学生同样可以进行简单的思维展示：

①明确三个量的表示：

“销售收入≥原收入+总投入”成立的前提下，确定销售价格和销售额。

通过对该题的剖析，学生将经历以上三个阶段的思维过程，将过程展示出来，思路清晰，每一步都能明确自己要做什么，从而成功地转化为函数最值问题的求解。倘若学生在每一次练习时都能养成剥题分析的习惯，也会降低对情境问题的畏惧，对解题能有很大的帮助，解题能力也会有提高。

三、作业可视化讲解，强化数学思维

在对学生可视化作业有了一定的要求后，教师就能更好地掌握学生的解题思路和流程，对于多数学生只能意会不能言传，更不能保证做对的情况，必须在课堂上对作业进行讲解，凸显正确解题思路和流程，然后予以强化训练。笔者认为，可视化作业的讲解通常可按以下程序完成：对情境进行剥离、明确相关关系、凸显正确思路、总结精简流程；有需要的时候，也可进行正误解题的对比。

例如，上题在进行情境剥离时，可将情境化简为：

（1）已知：每件售价25元，年销售8万元

预设条件：每提高1元，销售量相应减少2000件

求：销售总收入≥原收入，每件定价最多多少元？

（2）已知：每件售价25元，年销售8万元

这样从已知条件出发，去掉一些繁杂的内容，将题目的主要意思搞清楚，有助于学生找到相关量，确定相关量之间的关系。从已知条件、旧知识基础等方面分析，启发学生为什么必须确定这样的思路方向才有助于问题的解决。再用流程图的形式将思维过程凸显出来，可视化、可感化地突出正确的思维方式和解题程序，使学生对正确解题思路和流程得到强化。

通过教师对作业的可视化讲解，学生纠正了错误认识，明确了正确解题技能和解题思路的形成后，还需要专门的针对性巩固练习，通过练习解题过程和思路的可视化展示，可以促使学生不断地内化知识难点，细致地处理知识易错点。

总之，教师通过作业讲解的可视化，使学生在潜移默化中了解数学建模的解题思路、基本步骤和过程；学生通过作业思路可视化的强化训练，使自身对建立数学模型解决实际问题的技能得到锻炼，从而提升了数学建模素养和解决实际问题的能力。