基于高阶隐半马尔科夫模型的设备剩余寿命预测

刘文溢，刘勤明，周林森

(上海理工大学 管理学院，上海 200093)

0 引言

隐马尔可夫模型(Hidden Markov Model，HMM)作为一种概率统计方法，具有良好的随机性表征能力以及潜在结构关系描述能力，被广泛用于复杂系统建模领域。BUNKS等[1]首先将HMM从语音识别领域迁移应用于设备故障诊断领域，开创了故障诊断的全新研究方向；马伦等[2]从理论上阐明了HMM必须强制服从指数分布才能满足其马尔科夫性的不合理性，从而不能直接用于设备的寿命预测。

为了摆脱HMM本身特性的束缚，研究者们提出了改进的隐半马尔科夫模型(Hidden Semi Markov Model, HSMM)，将宏观状态进一步分为微观状态，并对每个宏观状态的时间分布做出先验假设，从而成功实现了隐马氏模型在剩余寿命预测领域的应用。董明等[3]假设HSMM的状态驻留为显式Gauss分布，并对设备进行了健康诊断与剩余寿命预测；LIU等[4]提出了信息融合的自适应隐马尔科模型，完成了对设备的诊断与寿命的预测，取得了良好的效果；李永朋等[5]等将Erlang分布引入HSMM模型，并对模型进行了重新推导，提高了识别率，降低了剩余使用寿命(Residual Useful Life,RUL)误差；原媛等[6]将HSMM输出的状态序列与比例故障率模型相结合，并假设基础故障率函数为两参数的威布尔分布。但上述研究均对模型关于时间的问题进行了先验分布假设，然而特定设备的先验知识通常难以获取，从而不可避免地带入了主观因素，影响了客观实际。

为了更好地参考历史统计信息以提高模型识别率，研究者们提出了高阶隐马尔可夫模型(Higher-order HMM，HOHMM)。针对高阶模型随之而来的参数爆炸问题以及更复杂的推导问题，研究者们建立了一种逐次降阶算法(ORED算法)来简化HOHMM，在此基础上提出了FIT算法(fast incremental algorithm)来训练HOHMM模型，并对其三问题分别进行了探讨[7]；相比于ORED算法的逐次降阶，HARDER等[8]提出了一种基于等价变换思想的HARDER算法，将任意高阶模型转化为对应的一阶模型。上述研究者为高阶模型的研究提供了一般研究方法，意义重大，但HOHMM在降阶为HMM模型过程中，都需要对模型的各个变量做相应的重新推导，并基于Baum-Welch算法对参数进行重估，且随着模型阶数上升，工作量也会呈现爆炸式的增长。ZHU等[9]建立了HO-HMMAR模型，进行了变量推导，更好地解决了最优投资组合问题；XIHONG等[10]建立了日均气温演化模型，并假设非对称分量为一个高阶隐马OU(Ornstein-Uhlenbeck)过程，结果表明该模型能有效地捕捉各种情况下的温度数据的特征

多项式拟合作为一种非线性拟合的简单工具，具有高效的数据处理能力。刘慧婷等[11]运用多项式拟合解决了EMD处理上下包络过程的端点问题，取得了良好的效果；VYAS等[12]运用多项式拟合的系数产生虹膜识别的特征向量，并通过基准IITD数据集和CASIA-v4区间虹膜数据验证了多项式方法的有效性。随着神经网络以及各种机器学习方法的普及，多项式拟合简单易用的闪光点在故障诊断领域愈发暗淡。但值得注意的是，多项式拟合是为数不多的能直接写出非线性关系解析式的方法，而这是神经网络做不到的。

参数估计问题一直是概率类模型最棘手的环节，随着工作量较大的最大期望(Expectation Maximization，EM)算法依赖于初值而易陷入局部最优的不足渐渐呈现，越来越多的研究者将目光转向各种智能优化算法。WU等[13]将遗传算法与灰色模型相结合，数值结果显示，结合遗传算法的新方法可极大地提高模型预测精度；KRAUSE等[14]采用基于遗传算法的函数逼近器估计感应电机参数，取得了较其他方法更好的效果；ZHANG等[15]运用人工免疫算法对HMM模型进行优化，得到了辨识度最高的初始观测矩阵；张小强等[16]运用自适应基因粒子群算法优化隐马尔科夫模型，得到了比传统HSMM更精确的结果。如何巧妙运用智能仿真算法简化隐马氏模型的研究过程，是未来研究中应当被重视的一点。

为了实现在分布未知前提下更加精确实际的预测，本文在上述研究的基础上，首先建立了基于HSMM的高阶隐半马尔科夫模型(Higher-order HSMM, HOHSMM)框架，在ORED算法和HARDER算法等价变换的启示下，提出一种基于排列的模型降阶方法，利用高阶隐马类模型的定义，使其可转化为相应的一阶模型，并让低阶模型三问题的解决方案能够用于高阶复杂模型。同时，对转移概率矩阵与观测概率矩阵进行相应的变形，使得高阶复杂模型中节点的相互依赖关系信息自然融入到模型参数之中，达到了简化模型的效果。其次，定义推导了辅助驻留变量，并利用智能优化算法群对携带了更多“依赖关系信息”的参数组进行估计，以极大化观测出现概率为目标，依靠参数组表征高阶模型的分解依赖关系，在一定程度上将复杂度从模型本身转移至参数组。紧接着，运用多项式拟合方法拟合各驻留变量序列，在分布未知的情况下完成了对设备剩余寿命的预测。最后，以美国卡特彼勒公司液压泵数据集对模型进行验证评价，结果显示本文方法是可行且有效的。

1 隐马尔科夫模型基础

1.1 一阶隐马尔科夫模型

一阶隐马尔科夫模型，即常规隐马尔科夫模型(HMM)，可描述为λ=(π,A,B)。由可观测的节点与隐状态节点组成，若令Statet为时刻t时节点所处的状态，隐状态节点状态之间的转移符合马尔科夫性即：

Prob(Statet|State1…Statet-1)=

Prob(Statet|Statet-1)。

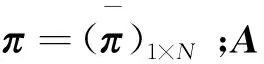
1.2 高阶隐马尔可夫模型

高阶隐半马尔科夫模型(HOHMM)是一阶马尔科夫模型的推广，保留了更多的历史统计信息。其假设所研究对象当前状态与之前数个状态有关。以一个n阶隐马尔科夫模型为例，其时刻t(t≥n+1)时的状态与前n个时刻的状态均有关，表示为：

Prob(Statet|State1…Statet-1)=

Prob(Statet|Statet-n…Statet-1)。

HOHMM模型虽然在保留更多历史统计信息的基础上提高了模型识别率，但其依然未能克服HMM模型自身的不足。

2 改进高阶隐半马尔科夫模型

本文在综合考虑HMM不足以及高阶建模优点的前提下，提出一种基于HSMM的改进高阶隐半马尔科夫模型(HOHSMM)。

2.1 基于排列映射的模型降阶

同样以一般意义上的二阶HOHSMM为例，由于二阶模型在结构上的变动，使得模型参数与相关算法随之产生变化。常规意义上，低阶模型三问题各自的解决算法并不适用于高阶模型，对此，本文提出一种基于组合映射的模型降阶法，实质是将二阶模型中相邻的两个时点所对应的隐状态结点合并为一个节点，并对合并后的节点进行马尔科夫过程建模，如图2所示。

其中图2a为在二阶HOHSMM模型上对模型的一个划分方式，将相邻状态节点合并为一个更大的“新节点”，此时新节点内部两个状态的关系对整个模型的马尔科夫性不产生影响，降阶后的新模型的马尔科夫性可由式(1)描述：

Prob(Statet,Statet-1|Statet-1…State1)=
Prob(Statet,Statet-1|Statet-1…Statet-2)(t≥3)。

(1)

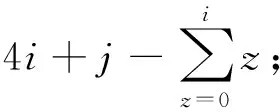
(2)

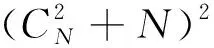
(3)

式中j为状态排列(i,j)中的第2个状态，以N=4的二阶HOHSMM为例，其降阶后的概率转移矩阵有效数据为20个，由表1稀疏表示给出，其中1和1*表示的位置为有效数据，1*所在位置列头代表的复合状态为主状态，1所在位置列头代表的复合状态定义为过渡状态，0表示的位置为无效数据。

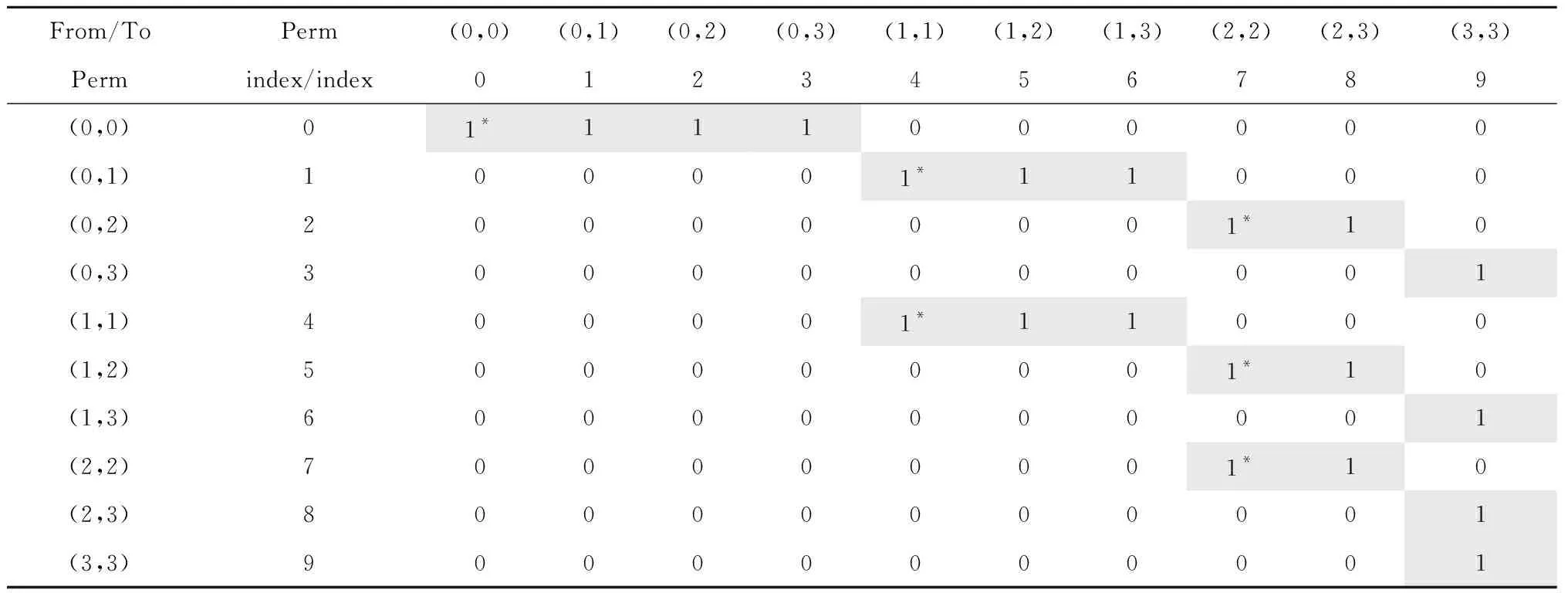
表1 状态数为4的二阶HOHSMM降阶转移概率矩阵稀疏表示

2.2 模型推理

借鉴前向-后向算法的思想，引入LT(linger time)机制并建立辅助变量ξt(i)，描述为式(4)：

ξt(i,d)=Prob(O[1:t],LT((i,j))=d|λ),t≥d。

(4)

意为在给定模型参数组λ下，截止t时刻产生观测序列O[1:t]以及在当前状态已驻留了d个时间的概率。

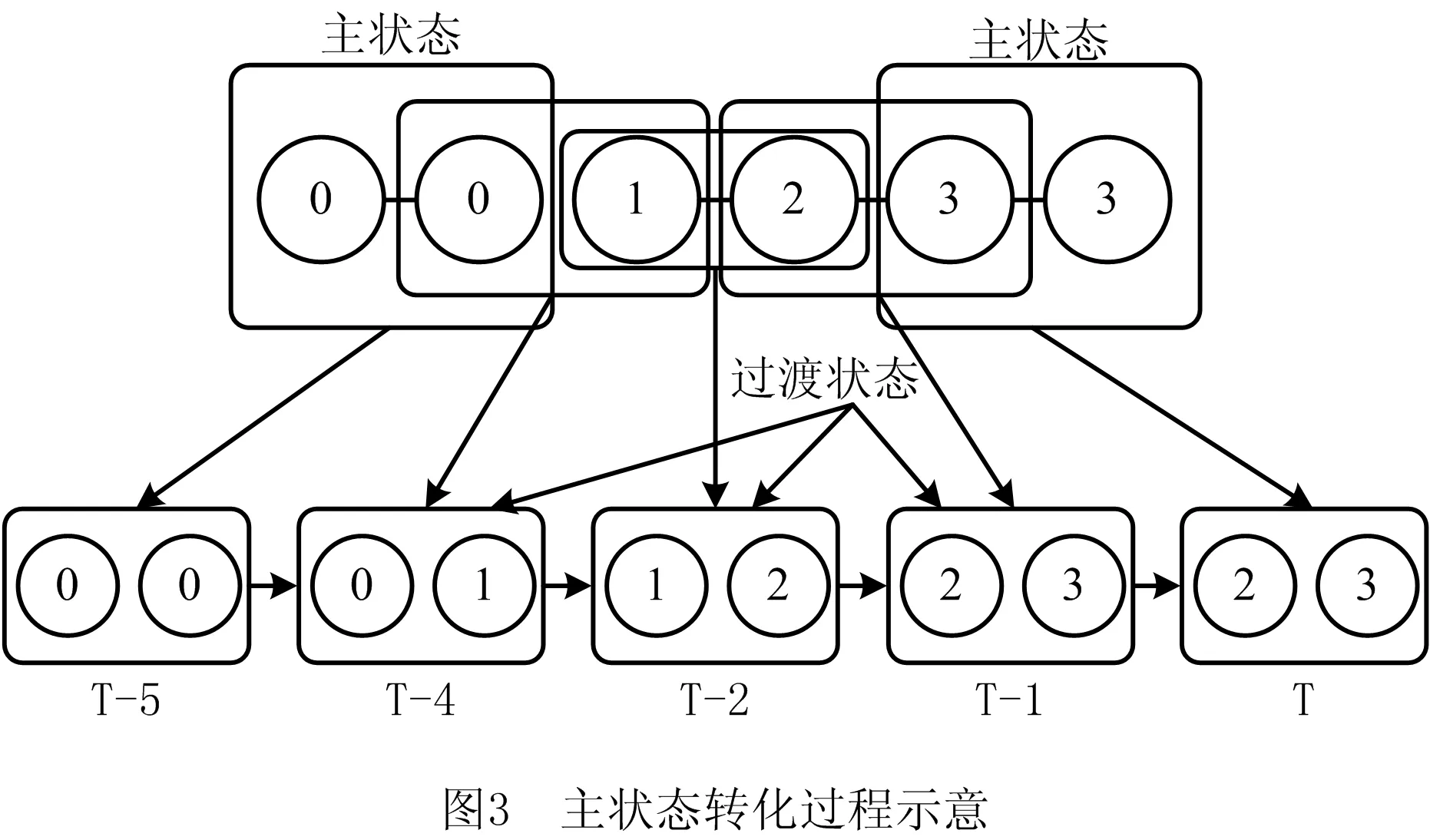
2.1节中给出了一般二阶HOHSMM模型转移概率矩阵的稀疏表示，并分别阐述了主状态与过渡状态的意义。不难得出，常规二阶模型不同主状态之间的转移是一个渐变的过程，即

主状态→(过渡状态序列)→下一主状态。

且该转化过程至多需要j-i+2个时点来完整描述，以状态主状态(0,0)转移至(3,3)为例，转移过程需要5个时点来描述，如图3所示。

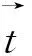
(1)当i=0时，d=t，ξt(i)描述为:

ξt(0,d)=Prob(O[1:t],LT(0)=d|λ);

(5)

递归初值为：

(6)

内转移递归式为:

(7)

(2)当i=1时，ξt(i)描述为:

ξt(1,d)=Prob(O[1:t],LT(1)=d|λ)。

(8)

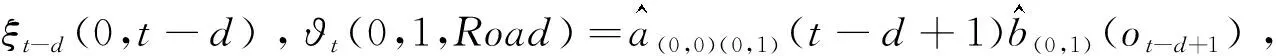
(3)当i=2时，承接状态可为(0,0)以及(1,1)，ξt(i)描述为：

ξt(2,d)=Prob(O[1:t],LT(2)=d|λ)；

(10)

内转移递归式为：

(11)

情形1当承接状态为(0,0)时，(0,0)～(2,2)需要4个时点刻画，承接值则为:

(12)

相应的ϑt(0,2,Road)可表示为:

(13)

相应的供归值为：

(14)

(15)

θt(1,2,Road)为:

(16)

供归值为:

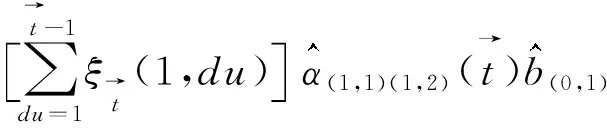
(17)

(4)当i=3时，承接状态可为(0,0)、(1,1)以及(2,2)，ξt(i)描述为:

ξt(3,d)=Prob(O[1:t],LT(3)=d|λ);

(18)

内转移递归式为:

(19)

情形1当承接状态为(0,0)时，(0,0)至(3,3)需要5个时点刻画，相应的承接值为:

(20)

ϑt(0,3,Road)可表示为:

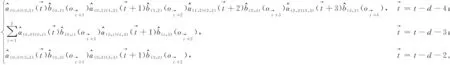
(21)

供归值为相应承接值与中间值的乘积。

情形2当承接状态为(1,1)时，(1,1)～(3,3)需要4个时点刻画，相应的承接值则为:

(22)

相应的中间值ϑt(1,3,Road)为:

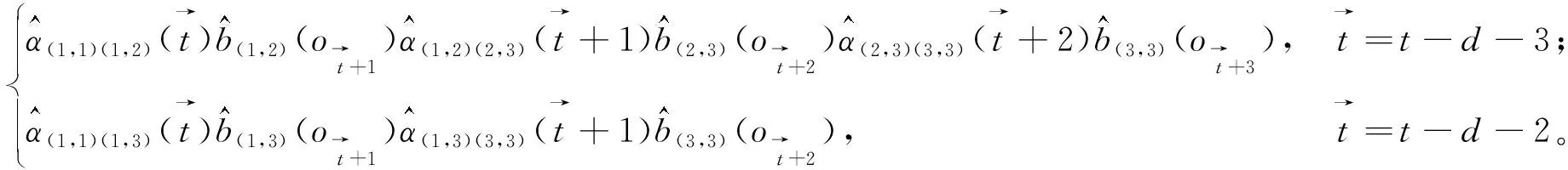
(23)

递归中值为:

(24)

情形3当承接状态为(2,2)时，(2,2)～(3,3)需要3个时点刻画，相应的承接值则为

(25)

相应的中间值ϑt(2,3,Road)为

(26)

递归中值为

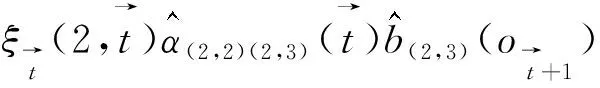
(27)

则ξt(i,d)的一般递归式可由式(28)表示：

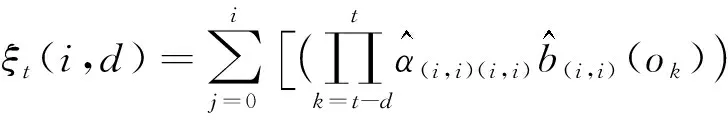
(28)

式中ct=t-d-lr+1，其中lr为Road的长度。

根据上述对递归式的分类推导，将状态较高时的辅助变量ξt分解到较其更低的辅助变量的表达形式，并在递归过程中，由计算机生成所有满足发生主状态转移的转移过程状态路径，遍历所有可能的转移状态路径便能计算得到任意ξt(i,d)，各主状态所包含的转移状态路径由表2给出，其中x不计入路径长度。

表2 各主状态转移过程路径生成器

在此基础上，给定模型参数λ，产生观测O的概率为：

定义辅助变量τt(index)，意为给定模型参数与观测的前提下，时刻t处于Mapping-1(index)的概率，即

τt(index)=

Prob(Statet=Mapping-1(index)|λ,O)。

τt+1(index)=

(29)

其对应的低阶模型中，时刻t时的处于单状态i(i∈(1,2,3,4))的概率用高阶模型表示为：

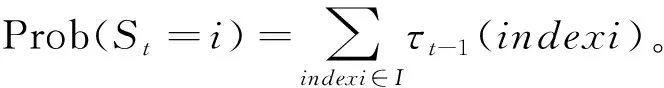
其中I为不同复合状态下第二子状态为i时对应索引集合，索引对应关系如表3所示。

表3 索引对应关系

二阶段似然函数为：

运用不同智能仿真算法来优化两阶段似然函数并进行比较，最终选取其中最优的结果。

3 不确定分布下的剩余寿命预测

2.2节中对各个状态驻留时间的递归推理，能得到设备在每个状态能够驻留时间以及产生观测的联合概率值。实际上，设备产生的观测以及设备在单个状态的驻留间存在着一定相关关系，该关系可由观测、状态转移矩阵通过特定的模式进行描述。为便于得到设备在各个状态驻留时间的边缘概率，不妨假设设备观测与驻留之间相互独立，则对于上述求得的ξt(i,d)，计算其所对应观测的产生概率Prob(O|λ)，则根据条件概率公式可得

使用各个时点所代表的时间来计算某一状态产生该段驻留的概率，得到一组驻留-概率序列数。通常在已知离散数据点的情况下，假设先验分布有利于研究数据的连续性特征，但如果错误假设数据分布，则拟合将存在极大误差，并且会丢失数据原有的性质。因此，本文采用一种基于多项式回归的方法去拟合未知分布下的数据，多项式回归方法可描述为：

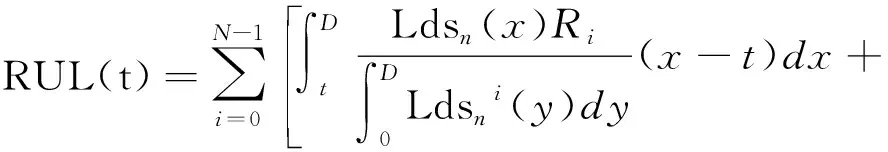
(30)

其中D为各个状态的最大持续时间，Prob(St=i)为时刻t时，设备处于状态i的概率，Ri,Rj为离散数据连续化后的积分缩放系数。

4 算例分析

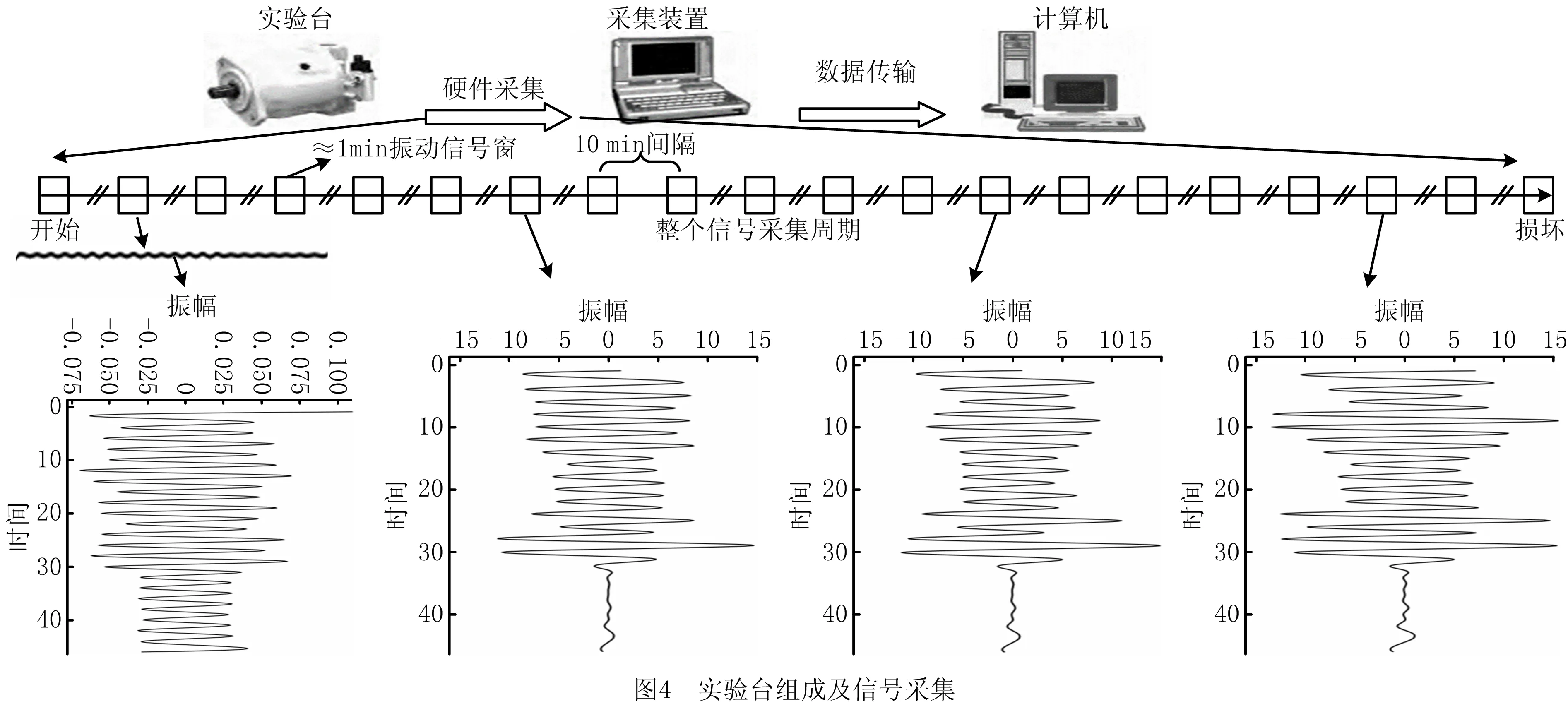
本文通过美国卡特彼勒公司液压泵的设备健康诊断与寿命预测实例来验证评价本文提出的模型与方法。实验室中设备的振动信号是由安装在与液压泵旋转轴平行位置的液压加速计收集。在应用实例中，分别对液压泵充入20、40、60与80 mg的微尘，并每隔10 min运用一个长度固定的时间窗采集一个约为1 min的振动信号(Pump6)。随后使用10dB的小波将振动信号分为五层，得到数组高频与低频小波系数，将经过降维后的小波系数作为DGHMM的输入特征序列向量。整个实验过程中，液压泵的状态可分为四种，分别为Baseline、Cont1、Cont2以及Cont3，其相应的代表性采样振动信号时域振幅情况如图4所示(Pump6)，其中Cont3状态为设备的彻底失效状态。整个实验分析平台为Python 3，平台运行环境为Windows 10。

4.1 部分数据预览

利用来自液压加速计振动信号监测数据，对液压泵进行健康状态诊断以及剩余寿命预测。部分经过小波变换后的振动数据(Pump6)如表4所示。

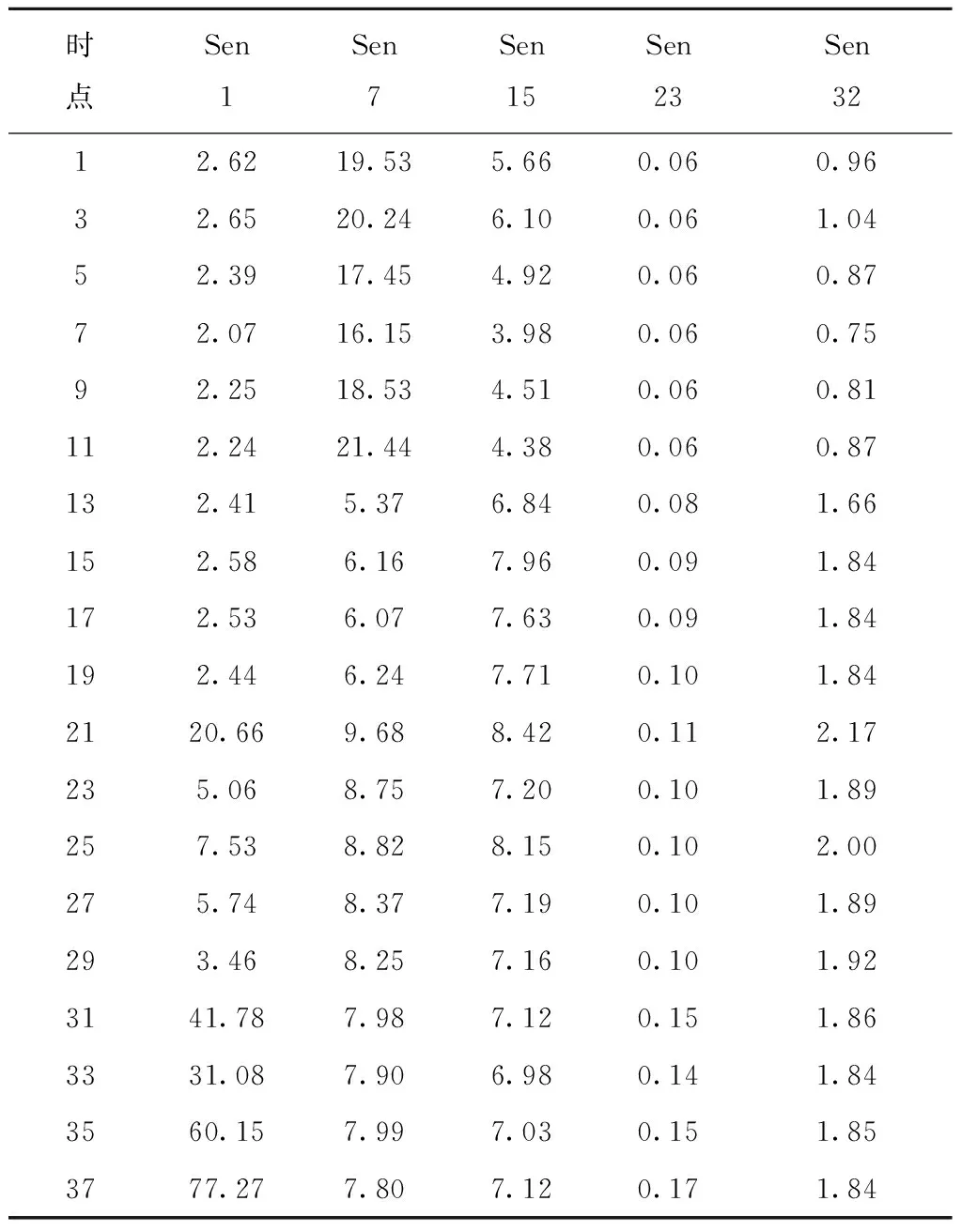
表4 Pump6部分小波变换数据

4.2 智能优化算法群参数估计

考虑最大期望算法对初值有较大依赖的不足，本文在模型框架下分别采用遗传算法(Genetic Algorithm, GA)、粒子群优化(Particle Swarm Algorithm, PSO)算法以及人工鱼群算法(Artificial Fish Swarm Algorithm, AFSA)对同一组全观测下的模型进行参数估计。最大迭代次数为300次，种群数(粒子群中为粒子数量)为30，其中GA采用大型参数自适应值编解码策略[17]；PSO算法采用定惯权重策略，惯性权重取值为0.5，学习因子均取2，；AFSA感知野取值1，拥挤因子取值0.6。以最大化观测出现概率为目标优化模型，迭代过程及结果如图5所示，在相同种群数量以及迭代次数前提下，遗传算法以持续进化以及最大似然而具有较好效果，3种优化算法各自所寻得的参数组的似然值如表5所示，得到降阶后的概率转移概率矩阵由表6给出。

表5 三种算法最大似然值

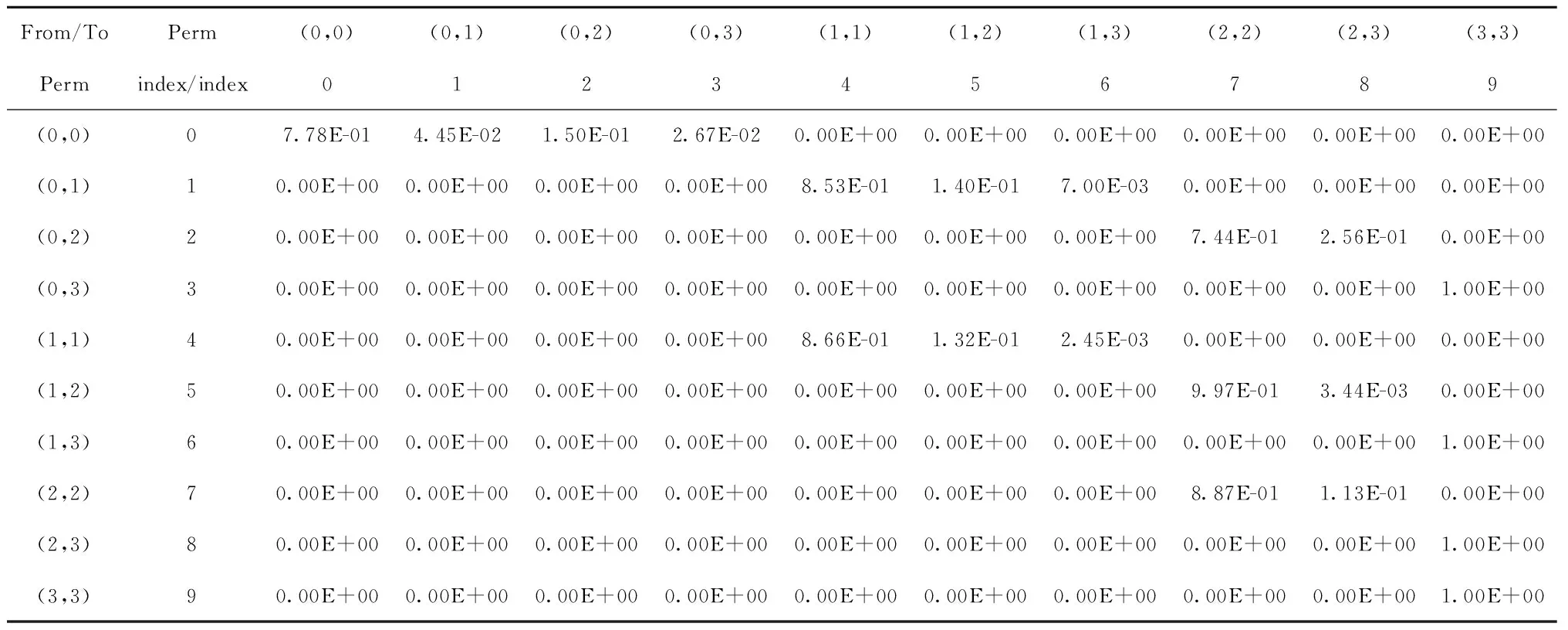
表6 最优概率转移矩阵稀疏表示

4.3 剩余寿命预测

基于模型推理，对各状态驻留进行分析，在计算过程中运用全概率公式进行等价替换。将不同时点每个状态不同驻留值按状态分开得到各个状态的驻留-概率序列，运用多项式回归对序列进行拟合得到各自的解析式，在拟合过程中优先选取对后续状态剩余寿命预测共振作用较小的阶数n(下称优先选取原则)。以最终时点4个不同状态的多项式拟合为例(如图6)，其中4个状态进行拟合的最优m值分别为：20、15、19、17，详细的多项式回归系数由表7给出。

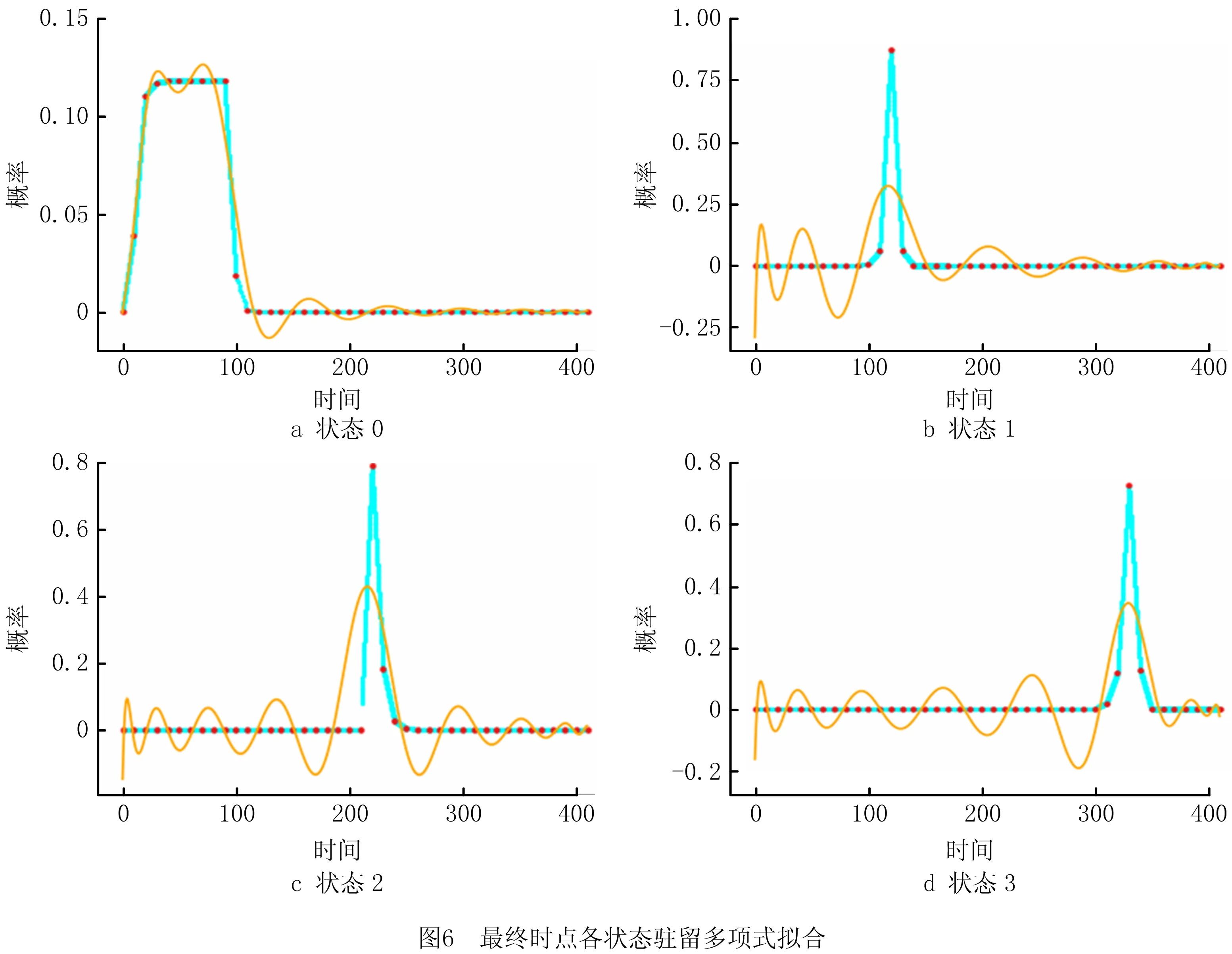
表7 最终时点多项式拟合系数一览

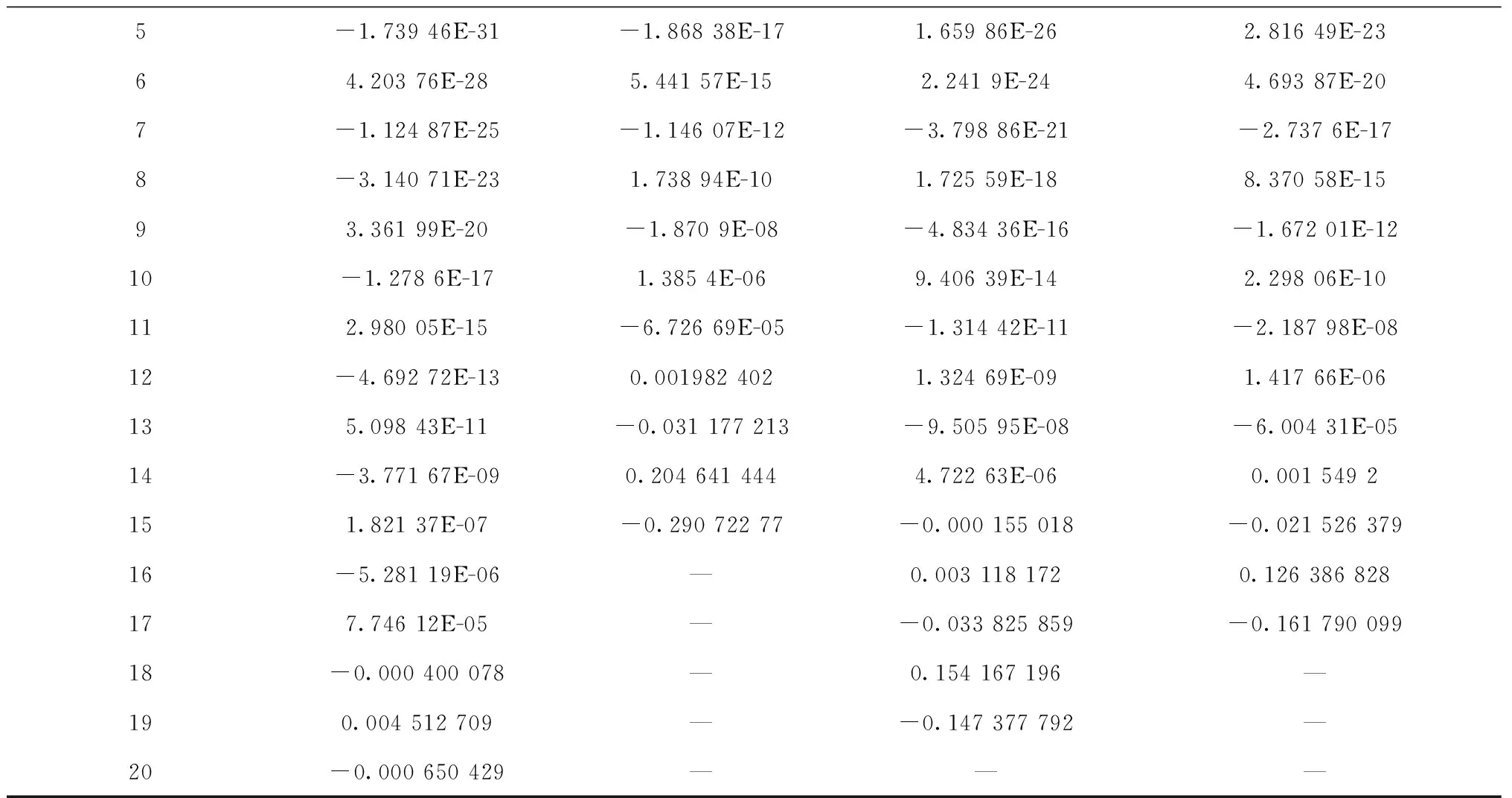
续表7

原则上概率的积分不允许负值出现，但多项式回归呈现明显的波动特性，即正负值存在一定的抵消作用，且不同状态相同时点也存在共振，不难预知预测的剩余寿命值可能存在一定的波动特性。在实验过程中，为了更好地进行多项式拟合，结合原始数据特点，对原始数据点进行了线性插值。图6中红色点为原始数据点，即自适应后的驻留产生概率值，浅蓝色为插值点，黄色线条为多项式拟合线。

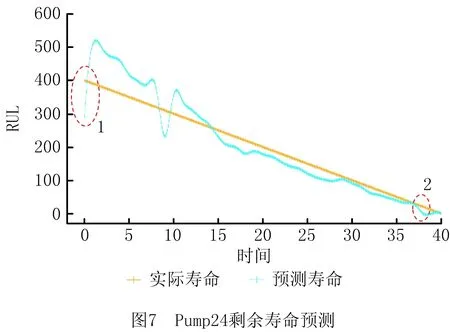
最终得到Pump24的剩余寿命预测情况如图7所示，其中离散预测点已进行插值平滑处理。一号标记处显示预测值在最终的时点处存在较大的偏差，对应图6各子图中多项式回归式初期波动幅度较大的现象，但波动随着时点的增加而逐渐变小，是优先选取原则的结果。二号标记处出现了“提前损坏”的现象，对应图6d中驻留提前降低的现象。

与低阶HSMM结果相比较[4]，本文模型预测的剩余寿命结果如表8所示，从抽样的时点来看，基于HOHSMM与多项式拟合的剩余寿命预测方法整体效果明显优于常规HSMM，算例表明，基于HOHSMM与多项式回归的寿命预测方法是有效可行的。

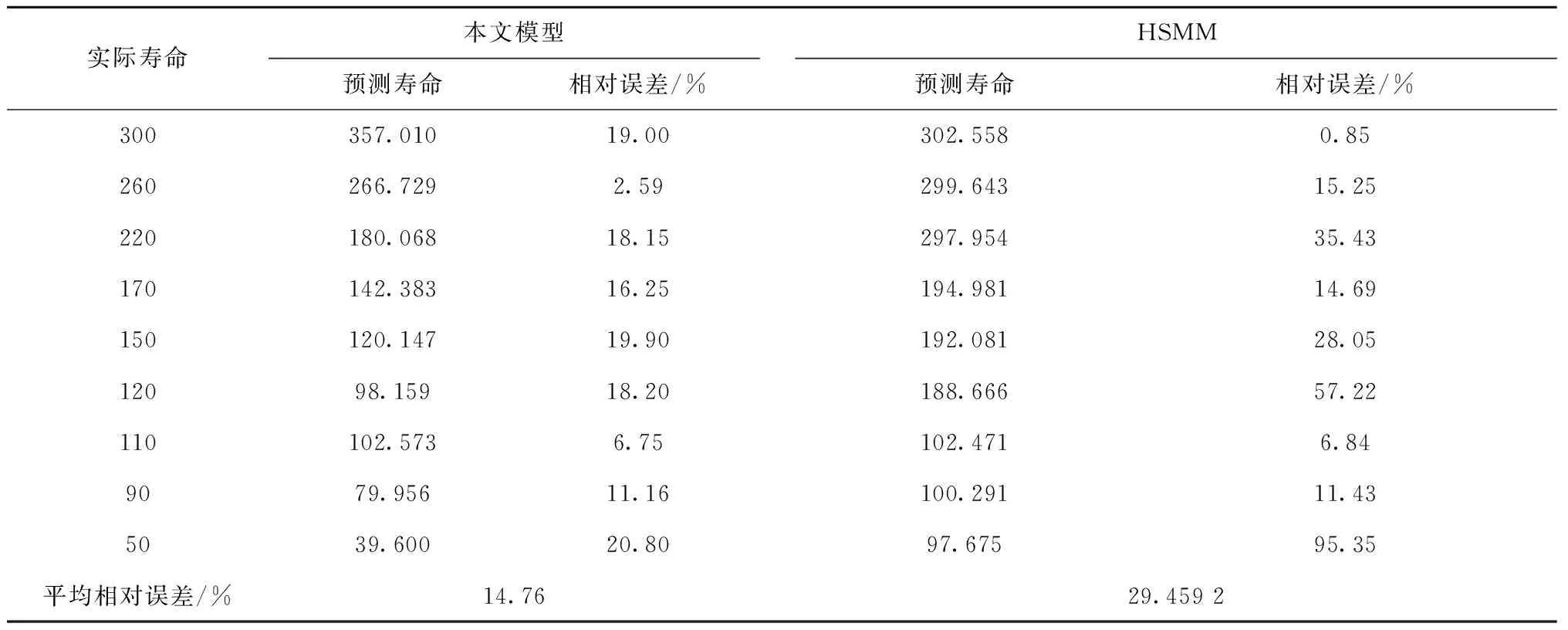
表8 预测剩余寿命相对误差分析

5 结束语

本文提出一种基于高阶隐半马尔科夫模型与多项式拟合的设备剩余寿命预测方法。其中排列组合的模型降阶方法简单直观，巧妙地利用了高阶隐马类模型的定义，使得高阶模型可通过转换观察角度的方法转化为相应的一阶模型，使低阶模型三问题的解决方案能够用于高阶复杂模型。通过智能优化算法群对本文模型进行了参数估计，将高阶模型之中复杂的依赖关系信息转移至变形后的参数组中，有效地简化了模型，为研究该类模型提供了一个新的思路，最后基于多项式拟合的剩余寿命预测从结果来看是有效的。

未来的工作重点应是考虑如何求得历史寿命与剩余寿命的联合分布，以便于修正模型所计算的剩余寿命。