基于数据挖掘技术的钛合金铣削工艺参数优化

刘献礼，孙庆贞，岳彩旭，李恒帅

(哈尔滨理工大学 先进制造智能化技术教育部重点实验室，黑龙江 哈尔滨 150080)

0 引言

随着工业自动化程度及信息集成度的日益提高，大量生产运行数据被企业收集。为了发掘数据中隐含的规律，为实际加工提供帮助，很多学者开始尝试利用数据挖掘技术从大量数据中寻找隐藏的信息，并利用这些信息指导实际生产加工[1-6]。针对机械加工工艺参数优化的问题，一些国内外学者提出利用搜索算法和数据分类算法进行分析计算。RAI等[7]以加工时间最短为目标，利用改进的遗传算法对铣削参数进行优化;LI等[8]基于一组有效数据的反向传播神经网络模型对切削参数进行预测;曾莎莎等[9]将神经网络法与遗传算法相结合，对薄壁件铣削加工工艺参数进行优化;LI等[10]通过对禁忌搜索(Tabu Search，TS)算法进行改进形成的新算法，对切削参数进行优化；SARDINAS等[11]以多目标优化为目的，通过改进遗传算法(Genetic Algorithm，GA)来获得车削过程中的最佳切削参数。以上算法通过严谨的逻辑运算进行分析挖掘，实现了加工工艺的优化，为指导实际生产加工提供了参考。

聚类分析[12]是数据挖掘中经常使用的分析算法，目前已被广泛应用于电商信息推送、物流网络构建、手术路径智能规划、电站锅炉燃烧效率提升等领域[13-15]。K-means算法[16]是一种经典的聚类算法，具有运用简单、优化迭代、快速收敛等优点。但在实际操作运行中，K-means算法也存在不能自主识别分类数目、过度依赖初始设置聚类中心等缺点。另外，算法在运行时会产生大量非最优性能指标集及其对应的运行参数集，对挖掘目标而言这些运行参数没有任何意义。为此，首先通过对算法添加分裂与合并操作得到迭代自组织数据分析算法(Iterative Self-organizing Data Analysis Techniques Algorithm， ISODATA)算法，实现算法在迭代过程中的自主识别分类数目；然后采用分步聚类的方法，在运行K-means算法之前对性能指标进行聚类分组,并将除最优性能指标组之外的其他性能指标分组进行约简，缩减数据库规模，减少无意义分组的产生。

随着智能工厂的普及，钛合金铣削加工中收集的力、热、振动等加工数据量呈指数增长，传统的数据分析算法已不能解决当前大量数据快速分析处理的需求，从而导致数据时效性的丧失。K-means算法在处理数据的过程中迭代总数随着数据量增加，收敛速度降低、耗时增加，已经不能满足数据时效性需求，寻求针对大量数据分析挖掘的方法已迫在眉睫。

云计算的出现满足了这种大量数据挖掘的需求。该技术通过将多台服务器连接成一个整体，实现了计算能力及存储能力的快速提升[17]。Hadoop是目前广泛使用的云计算工具，其核心构件是分布式文件系统(Hadoop Distributed File System， HDFS)和并行计算框架MapReduce[18]。通过将传统算法与MapReduce框架结合，实现了算法的并行化，该模式已成为目前大量数据快速处理最有效的方法。

针对大批量、单一、高附加值钛合金产品生产加工过程中产生的大量运行数据，为探究数据中工件表面粗糙度与加工工艺参数之间的关系，实现工艺参数的优化，本文提出一种基于云计算平台Hadoop的分步聚类方法。利用Hadoop大数据分析平台，将有限的计算资源进行整合，提升了面对海量数据的挖掘处理能力，通过引入分步聚类理念对K-means聚类算法进行改进，形成新的高效聚类算法T.K-means，新算法提升了聚类的效率与挖掘结果的可读性。该算法挖掘出的加工工艺参数反应了历史加工数据中工件表面粗糙度的最大可达值，该参数对实际生产加工具有指导意义。

1 基于分步聚类和并行计算的新算法

1.1 K-means算法

K-means中心聚类算法[19]是一种基于划分聚类的经典算法，其基本思想是:首先明确每一个数据点只会存在于一个聚类中，选择K个不同的起始聚类中心点，然后所有样本数据均计算与每一个中心点的距离或者相似度，而每个样本会根据最小距离或最大相似度被分配到与其最相似的聚类中，并根据这些数据样本重新计算每个聚类的新中心，通常以标准测度函数衡量划分的结果，具有最小标准测度函数值的划分即为最终分群。标准测度函数一般采用类内平方误差之和D来表示，

(1)

式中：K为类的总数，xi为类Si的平均值。

划分聚类将相似的数据集进行聚合(数据集包括性能指标A与工艺参数B)，若有一定量的Bi对应Ai，则表明在工艺参数Bi发生的情况下性能指标Ai会发生。寻找到最优性能指标对应的加工工艺参数是本次划分聚类挖掘的最终目的。

1.2 ISODATA算法基本内涵和步骤

1.2.1 ISODATA算法的基本内涵

ISODATA算法由K-means算法改进而来，与K-means算法相比，改进算法能够进行动态聚类或迭代自组织数据分析。ISODATA算法聚类中心的计算与K-means算法相同，通过类内样本均值来决定，但是ISODATA算法能够在初始聚类时认识到数据的本质属性，并通过模仿人类认识事物的过程以一种逐步进化的方式来逼近事物的本质，从而更加科学的进行分类。

1.2.2 ISODATA算法步骤

ISODATA算法需要确定以下参数:K为预设的聚类个数；θS为类中样本标准差最大值；θC为聚类中心之间距离的最小值；θN为各类中至少具有的样本数；L为在一次迭代中可以合并的类的最大对数；I为迭代的极限次数。

ISODATA算法的挖掘过程主要分为以下5个步骤：

(1)首先，在所有数据中随机选取k个任意样本以此当作初始聚类中心z1，z2，z3，…zk，这里k与K不一定相等。对上述6个参数进行设定，运行算法将所有数据样本分配到距上述k个中心点最近的类中。

(3)～(4)对前一次的聚类结果进行合并或者分裂处理。由于分类数目过少或者某一类中样本数目过大，通过分裂处理可以发现空间上更多的聚类中心；由于两类或多类中的数据样本存在距离过近的情况，彼此之间有较强的关联性，通过合并处理可以使各类之间具有明显的区别。通过以下具体方案获得新的聚类中心。

分裂操作：首先计算每个聚类中样本距离的标准差向量σj,然后求出所有标准差向量σj中的最大分量σmax，若有σmax>θS，同时又满足Hj>¯H和Nj>2(θN+1)，即Cj中样本总数超过规定值一倍以上或者k≤K/2，则将zj分裂为两个新的聚类中心zj+和zj-，且k加1。

(2)

合并操作：计算全部聚类中心的距离：

Hij=‖zi-zj‖,
i=1,2,…,k-1,j=i+1,…,k。

(3)

比较Hij与θc的值，将Hij<θc的值按最小距离次序递增排列,将距离最小的两个聚类中心合并，得到新的中心为：

(4)

式中两个聚类中心向量分别以其类内的样本数进行加权，每合并一对，则k减1。

(5)重新进行迭代运算，持续上述过程，直到聚类结果收敛。

通过ISODATA算法的分裂与合并操作，实现了海量一维数据的自动聚类，为后续准确寻找各分组对应的优化数据集提供了条件。

ISODATA算法流程图如图1所示。

1.3 Hadoop平台及MapReduce架构

Hadoop兼具高可靠性、高扩展性、高容错性和高效性的特点，能够对海量数据进行快速处理。本文基于Hadoop架构搭建了Cloudera公司的发行版，将该版本称为CDH(cloudera distribution hadoop)大数据分析平台[19]，平台架构如图2所示。

分布式文件存储系统HDFS是一个高容错的系统，可以检测和应对硬件故障，能够部署于低端通用硬件上。HDFS将每个节点上的本地文件构建成逻辑上的整体文件系统，提升了数据存储的能力，从而为海量数据的存储提供了有效的解决方案。HDFS的架构是基于一组特定的节点构建的，其中Namenode(仅一个)在HDFS内部提供元数据服务，Datanode(若干个)为数据提供存储块。

并行计算框架MapReduce是一种分布式计算模型，能够实现计算的并行化。计算的并行化是目前海量数据处理的主要方式，并且一些经典的数据挖掘算法已在编程人员的努力下实现了与MapReduce并行计算框架的结合，成为并行算法[20-22]。MapReduce框架中，JobTracker负责初始化作业、分配作业，称为主控节点；TaskTracker负责与JobTracker进行通信，协调、监控与执行整个作业，称为从节点。MapReduce用于大数据计算，它屏蔽了分布式计算框架细节，将计算抽象成Map和Reduce两部分。经过Map阶段对数据的初步处理，生成“键—值”对形式的中间结果，在Reduce阶段则会对中间结果中相同“键”的所有“值”进行规约，经过上述计算过程得到最终结果。并行计算框架MapReduce的工作流程如图3所示。

1.4 新算法的工作流程

将ISODATA和K-means两种算法分别与MapReduce并行计算框架相结合，实现两种算法的计算并行化。首先通过ISODATA算法对性能指标进行聚类，实现对数据库的约减，然后利用K-means算法完成对优化目标的聚类，最终形成一个高效聚类算法——T.K-means。与传统的K-means相比，新算法通过对性能指标与优化目标递进聚类，减少了不相关数据的规模，提升了聚类结果的可读性，通过避免对数据库的反复检索，挖掘效率得到极大的提高。

具体实施过程中，T.K-means算法的步骤是:

(1)提取数据库中性能指标数据集，利用ISODATA算法对性能指标集进行聚类，根据聚类结果，剔除非最优性能指标分组及其对应的工艺参数集。经过上述处理，原数据库中数据规模减少，新的数据集形成；

(2)在HDFS存储系统中，新的数据集将会被平均分配到若干个存储文件中，并且在处理开始时这些文件会随机分配到任意工作节点；

(3)Map阶段，被分配的数据存储文件会在对应节点进行扫描，运用K-means算法，产生部分聚类中心及各聚类中心所对应数据样本，生成键值对，其中key代表聚类中心，value代表对应聚类中心的数据样本；

(4)Reduce阶段，将会对Map阶段生成的键值对进行分析处理，新的聚类中心通过相同key对应所有数据样本的平均值进行计算，并输出其对应的新的数据样本；

(5)判断聚类中心向量是否收敛，若收敛，则跳转到步骤6，否则转步骤3；

(6)针对最后一次生成的聚类中心向量，对原始数据进行分类，得到最终的聚类中心及其对应数据样本。

T.K-means算法流程如图4所示。

2 T.K-means算法在钛合金铣削加工工艺参数优化中的运用

2.1 挖掘目标的确定及挖掘架构

钛合金铣削加工中，被加工工件表面粗糙度直接影响工件的化学、物理及力学性能，而且产品的可靠性、工作性能和寿命在一定程度上取决于主要零件的表面粗糙度，并且加工工件表面粗糙度是企业加工能力的象征，直接影响企业的效益，因此选择加工工件表面粗糙度作为性能指标。

将T.K-means算法应用于钛合金铣削加工工艺参数优化中，最终得到“优化工艺参数→最优性能指标”的聚类规则，在此规则下可以认为利用上述工艺参数即可得到钛合金加工的最优性能指标，该工艺参数即可作为优化目标值用以指导实际钛合金铣削加工。

工艺参数的选择需满足以下两个条件：与工件加工表面粗糙度密切相关；在实际运行中可进行调控，能够对实际运行进行指导。根据上述条件选出以下工艺参数:铣削速度、进给速度、铣削深度和铣削宽度。

基于数据挖掘技术，以钛合金加工表面粗糙度为性能指标，利用T.K-means算法对工艺参数进行优化。如图5所示为基于数据挖掘技术的钛合金铣削工艺参数优化架构图。

2.2 挖掘数据的来源

目前缺少大量的实际加工数据用于分析，本文采用响应曲面法建立铣削参数与性能指标的数学模型，并通过此模型所生成的大量虚拟数据来代替真实数据进行分析[23-24]。实验使用大连机床公司VDL-1000E型三坐标立式数控加工中心机床，选用厦门金鹭公司整体硬质合金立铣刀，型号为：ST210-R4-20030；实验试件为Ti-6Al-4V钛合金板材，铣削方式为单齿、顺铣，冷却方式为干切削；使用SR-200型手持式表面粗糙度测量仪对表面粗糙度进行测量，为保证测量精度，对被测表面进行3次测量并取平均值，以此作为最终表面粗糙度测量值。实验现场如图6所示。

通过响应曲面法建立铣削参数与表面粗糙度间的数学模型：

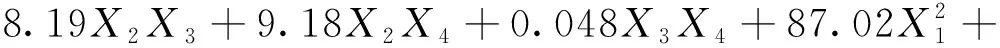
(5)

式中：y为表面粗糙度的预测值；X1、X2、X3、X4分别为每齿进给量、切削速度、轴向切深和径向切深。

对拟合的方程进行方差分析，方程P<0.000 1，表明该方程拟合水平极好；而失拟项的P= 0.055 6>0.05，表明失拟水平不显著。校正系数值R2为0.883 2，表明该模型对响应值的解释度达到了88.32%，能够较好地反应工件表面粗糙度与4个切削参数的关系。

真实加工过程中存在机床振动、刀具质量不同等问题，本文通过设置随机数m来解决上述问题对工件表面粗糙度所带来的影响，并保证其值在合理的范围之内。

y1=y+m%y。

(6)

4个铣削参数的范围分别为：vc∈[80,120]，fz∈[0.08,0.14]，ae∈[0.5,1.5]，ap∈[8,12]；随机数m∈[-10,10]。在指定范围内设定上述5个参数：vc按照40/19的间隔取值，fz按照0.01的间隔取值，ae按照0.5的间隔取值，ap按照4/19的间隔取值，m随机取值。将m代入式(6)中,共生成8万条加工数据，以此代替真实加工数据进行分析。

2.3 数据的预处理

由于人为疏忽、设备异常等因素，往往会出现数据误植、数据遗失或数据不一致、重复、矛盾等不同类型的数据问题，无法直接进行数据挖掘或挖掘结果差强人意。从数据库所有存储数据中筛选出2.2节所述工艺参数和性能指标对应的数据。将提取数据中存在明显异常的数据进行删除，采用凝聚层次聚类等相关操作剔除离散点数据，针对一个工艺参数对应多个性能指标的情况，为保证分析数据的合理性，对多个性能指标数据求取平均值，以此作为该工艺参数对应的性能指标值。经过以上处理，基本完成数据的预处理工作。

2.4 Hadoop平台的配置

首先在各节点VMware(虚拟机)上安装Linux操作系统，设置多用户，并对用户权限做出设定(一般用非root用户对Hadoop平台进行操作)，然后设置SSH免密码登录(普通用户下)，在保证安全传输数据的同时，实现各节点间信息无密共享。配置JDK环境，解压并安装Hadoop2.7.2，在此期间需要注意Hadoop与JDK的安装路径保持一致(JDK是安装Hadoop的基础环境)。最后通过对基础文件的修改、配置实现Hadoop平台的搭建，这些文件主要包括hadoop-env.sh，conf/core-site.xml，conf/mapred-site.xml和conf/hdfs-site.xml 共4个。其中通过修改hadoop-env.sh文件来添加Java运行环境，通过hdfs-site.xml对HDFS的相关信息进行配置，通过core-site.xml对架构内部属性进行配置，通过conf/mapred-site.xml对并行计算框架MapReduce的相关信息进行配置。经过上述配置，其运行环境已经搭建完成，在根目录对存储框架HDFS执行格式化命令，即可启动Hadoop运行环境。

2.5 挖掘结果

利用T.K-means算法对所选工艺参数及被加工工件表面粗糙度数据进行挖掘。在数据进行预处理后，利用ISODATA算法对原始数据进行约减，设定算法所需参数其中预设的聚类个数为100，类中样本标准差最大值为0.5，聚类中心之间距离的最小值为0.03，各类中至少具有的样本数为200，在一次迭代中可以合并的类的最大对数为2，迭代的极限次数为200。首先对性能指标进行分组，通过聚类将工件加工表面粗糙度分为0.210～0.235 μm，0.242～0.273 μm，0.279～0.291 μm等27个分组，找到最优工件加工表面粗糙度组为0.210～0.235 μm，删除剩余的工件加工表面粗糙度组及其对应的工艺参数集，最优工件加工表面粗糙度组及其对应的工艺参数集即为全部数据集的一个约简。工艺参数数据规模由8万条减少为2 317条。

利用SQL语句从数据库中寻找表面粗糙度在0.210～0.235 μm所对应的全部铣削参数组合，再次利用ISODATA算法对其进行分组。首先大致了解数据的分组数，在Hadoop平台上设置10个分组数与最大迭代次数30次，依据算法流程对已完成约简的数据进行挖掘，寻求指向最优工件表面粗糙度分组的工艺参数聚类分组，打印在控制台的聚类结果如图7所示。

经过整理，最优工件加工表面粗糙度0.210～0.235 μm组对应的工艺参数数据分组如表1所示。

2.6 结果分析

以该机床铣削钛合金的加工数据的挖掘结果为例，上述聚类的意义是当工艺参数处于表1中分组范围内时，就有较大的概率使工件加工表面粗糙度在最优范围之内。表1中所示区间即为这些工艺参数的目标值，本文选择各分组区间中心值作为优化目标值，来直观的显示目标值的结果。最优工件加工表面粗糙度中心值为0.227 μm，对应的工艺参数优化目标值如表2所示。

表1 聚类的结果

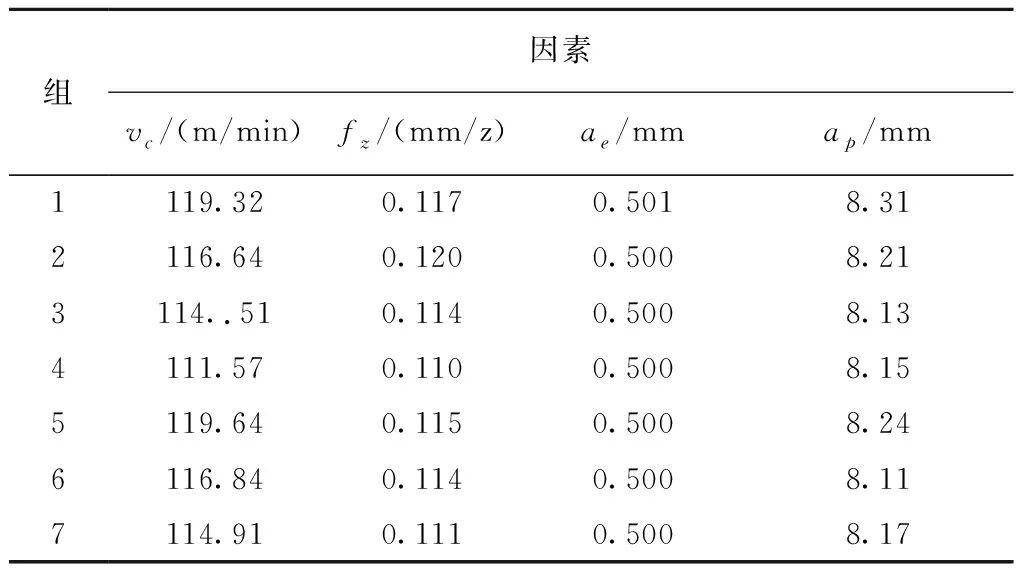
表2 工艺参数优化结果值

针对所研究的机床，可按照表2中优化目标值对各参数进行调整，使钛合金加工表面粗糙度在0.210～0.235 μm区间内，进而保持机床在最佳状况下运行。将最优工件表面粗糙度与所有铣削参数运行产生的工件表面粗糙度的平均值进行比较，优化值是0.227 μm，所有数据的平均值0.674 μm，工件表面粗糙度提升了0.447 μm，达到了提升工件表面粗糙度的目的，并将以下工艺参数优化结果值代入式(3)中，为保证m值取值的合理性，取其平均值0代入式(3)中，所得表面粗糙度值均在0.210～0.235 μm范围内。

由表2可知，利用T.K-means聚类算法对原始数据进行挖掘，最终优化结果只显示优选后的7组工艺参数数据。对原始数据采用ISODATA算法进行聚类运算，共产生113个聚类分组。两者相比，利用T.K-means聚类算法，聚类结果可读性更高，并且避免了因找寻最优加工工件表面粗糙度及其对应工艺参数聚类分组所花费的过多时间。

3 结束语

本文在云计算环境下，引入分步聚类理念，对K-means聚类算法进行改进，并将改进后的新算法与MapReduce计算框架相结合，实现算法运算的并行化，最终形成了一种新的高效聚类算法：T.K-means算法。将T.K-means算法应用到以减小TC4钛合金工件表面粗糙度为目标的工艺参数优化中，得到以下两条结论：

(1) T.K-means算法以分步聚类理念为基础，将性能指标与工艺参数分别进行聚类，减少了算法反复检索数据库的次数，并且避免了产生无用聚类候选分组，提升了聚类的效率与聚类结果的可读性，并将算法与MapReduce并行计算架构相结合，实现了算法的并行化，整合了有限的计算资源，解决了传统算法面对海量数据挖掘能力不足的问题。

(2) 通过T.K-means算法对虚拟钛合金铣削加工数据进行挖掘，寻求到“优化工艺参数→最优表面粗糙度”的聚类规则，得出最优表面粗糙度组对应的可调控工艺参数的范围，挖掘出的加工工艺参数反应了所有数据中工件表面粗糙度的最大可达值，可以论证当具有大量真实加工工艺及其对应的性能指标数据时，所挖掘出的聚类结果可用于指导铣削钛合金加工工艺参数的优化。