数据驱动构造流程工业系统状态特征谱的方法

陈 倩,孙 锴，2+

(1.西安建筑科技大学 机电工程学院，陕西 西安 710055；2.中国科学院 微电子研究所，北京 100029 )

0 引言

以能源重化工企业为代表的流程工业系统在我国国民经济中起着极其重要的作用，是我国制造业不可或缺的组成部分。流程工业系统由一系列复杂的机电设备组成，各设备种类和数量庞大，是一类典型的分布式复杂机电系统，其生产对象多数属于高温、高压、易燃易爆等物质，发生火灾、爆炸、污染物泄露和人员中毒等安全事故的概率远高于其他生产企业。在流程工业系统中，生产设备的安全管理与运行健康状态监测是永恒的主题[1]。

流程工业系统内部结构较为复杂，各设备之间联系紧密，具有高度耦合性，导致需要监测和控制的回路数数以千计，并且传感器需将监测到的数据实时地上传给分布式控制系统，因此其分布式控制系统实时记录着整个系统的运行数据，保存了所有的系统特征信息。系统在连续生产过程中产生的物质流、能量流和信息流三者之间相互交换，导致系统监测数据日益剧增，具有海量性、耦合性和非线性关系，很难建立数学解析表达式[2-4]。从系统层面直观地展示系统的运行健康状态及动态演化过程，对于分析复杂机电系统的运行状态至关重要。

分布式控制系统(Distributed Control System，DCS)数据集是由数以千记的时间序列构成，本质上是一个多元时间序列。传统的DCS数据分析法广泛采用多元统计分析方法[5-7]，具有代表性的有主元分析法(Principal Component Analysis, PCA)[8]、独立分量分析法(Independent Component Analysis, ICA)[9]、偏最小二乘算法(Partial Least Squares, PLS)[10]、核主元分析(Kernel Principal Component Analysis, KPCA)[11-13]、神经网络-PCA分析(Neural Network-PCA, NN-PCA)[14]和核独立分量分析(Kernel Independent Component Analysis, KICA)[15-17]等。其主要思路是采用多变量映射方法对数据进行降维，提取少量“关键”因素数据进行分析，忽略掉大多数“非关键”信息。从历次安全事故的事后分析来看，被高度关注的“关键”因素一般来说都运行正常，而造成事故的正是所谓的“非关键”因素。这是由于流程工业系统本身所特有的设备间高度的关联性和耦合性，导致从系统工程理论的角度来看不存在“非关键”数据。因此，不降维分析DCS的所有数据是准确提取企业级系统运行健康状态信息的重要前提，也是数据分析领域面临的重大挑战。

为了避免数据降维，解决数据之间高度耦合的问题，数据可视化的方法得到了广泛的使用[18-20]。鲁文波等[21]通过近场声全息重新构建机械声压场和声源的可视化声像图，从声像图中提取出灰度共生的矩阵特征，采用支持向量机(Support Vector Machine, SVM)模式识别达到故障诊断的效果；LU等[22]提出了声全息图方法，通过对比正常状况和异常状况时的灰度图像，实现了机械设备非接触式的故障模式识别；杜党党等[23]提出一种基于故障彩色图谱的发动机故障模式识别方法；邴绍强[24]通过构造采油生产知识图谱及建立预警规则方法,研制了一套智能预警系统；刘鑫等[25]用灰度图表征时域振动信号，提出一种基于灰度图像纹理分析的二维故障特征提取模型。孙锴等[3,26]将数字图像处理技术引入到DCS数据分析中，定义了色彩相空间，将DCS监测数据集转化为数字图像，制定了构造系统图谱，以图像的形式反映系统运行状态特征的方法，有效地展现了多变量数据间的内在关系，从宏观层面将多变量数据间的高耦合性、非线性关系直观地呈现出来。其中，系统故障图谱将监测数据分为正常数据和异常数据两类，分别以白色和黑色对数据进行着色，以黑白二值图像反映了系统中异常数据的分布特征。然而，仅将监测数据划分为正常和异常两类过于简单，降低了分析的准确性，无法满足企业生产要求。对于流程工业来说，一次停机或大修的成本代价很高，企业工程师需要了解数据的异常程度作为维修设备的依据，而系统故障图谱简化了数据异常程度信息。

为了解决上述问题，本文提出了构造系统状态特征谱的方法，在系统故障图谱的数据分类基础上对DCS监测数据集中所有数据按照偏离最优值的程度进行了细化分类和着色，最大限度地保留了数据异常程度信息。通过对系统状态图谱中像素点的位置以及色彩的分布规律进行分析，可以更加准确地对系统的整体运行健康状态做出判断。

1 数据矩阵X

DCS监控数据集可以被看作是一个多变量时间序列集，其中包含了n个监测变量的时间序列。每经过一个采样时间间隔，对各个监测变量参数进行一次采样，每个变量在一个监测时间间隔内可以截取m个采样值。将采样监测变量作为行向量，采样时间序列作为列向量进行排布，可以构造出一个m×nm×n的二维矩阵X。n个监测变量构成n维Hausdorff拓扑空间S∈Rn，m个采样周期构成m维Hausdorff拓扑空间D∈Rm，系统监测数据集由它们的笛卡尔乘积空间S×D∈Rm×n构成，这是一个m×n维的Hausdorff拓扑空间。定义一个二维Hausdorff拓扑空间X∈R2，建立映射关系f:S×D→X，将蕴含复杂机电系统运行健康状态的 DCS监测数据集投影到二维数据空间中。

定义1数据矩阵X。本文将既能反映复杂机电系统的时间和空间分布，又能反映系统运行健康状态的矩阵，称为分布式复杂机电系统的数据矩阵X，

(1)

式中xijxij表示第j个监测变量在第i个采样周期的数值。数据矩阵X的行向量Xi∈Rm表示系统的n个监测变量在时刻i的一个采样值，代表着某个特定时间点的系统动态特性。数据矩阵X的列向量Xj∈Rn表示系统的第j个监测变量的时间序列。

2 分类矩阵Q

根据企业生产的实际工况，挑选出系统处于运行状态最佳时段下所监测到DCS数据集，并将该数据集中的数据作为评判系统运行状态的基准，即DCS标准集。通过DCS标准集中各列向量的平均值和方差，得到最优监测值向量E和异常偏离度G作为待测数据集的分类的基准向量。

2.1 数据分类器T

定义2最优监测值向量E。对DCS标准集所构成的数据矩阵中的每一列求平均值，可以得到其均值行向量，将该均值行向量称为最优监测值向量E：

(2)

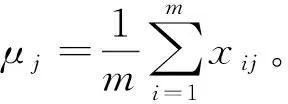
定义3异常偏离度G向量。对DCS标准集所构成的数据矩阵中的每一列求标准差，所得到的系统标准差行向量称为异常偏离度向量G,

(3)

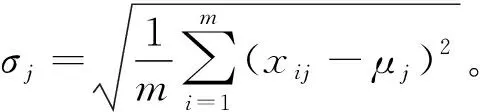
定义4标准质量区间。根据异常偏离度对DCS监测数据进行分类的基准区间。当变量j的监测数据在标准区间中时，表明系统处于最佳运行状态，如式(4)所示：

μj-σj≤xj≤μj+σj。

(4)

根据定义2和定义3，将传感器变量j的监测数据划分到不同的质量间隔中，如图1所示。图中h表示偏离标准值的异常偏离值，偏离标准区间的值越高，表示系统的运行故障程度越高。

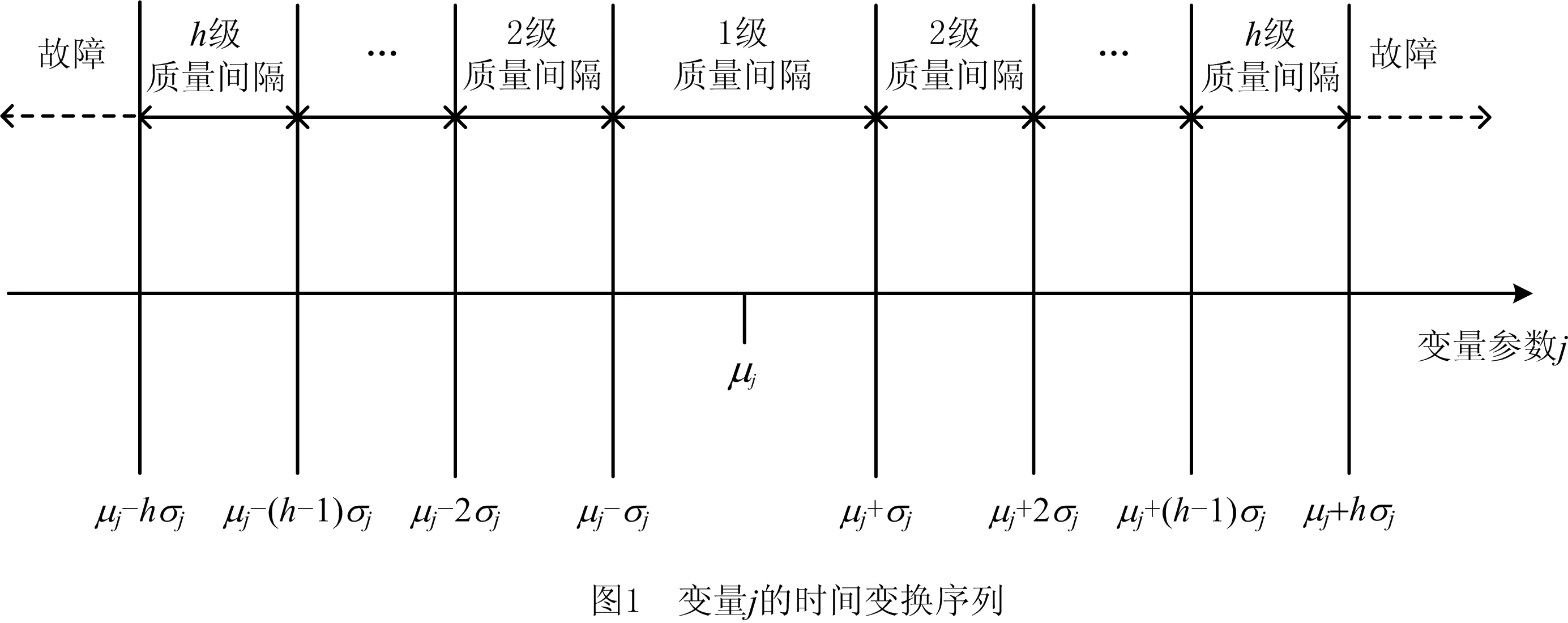
根据标准质量区间，将每个参数变量在一段采样周期内监测的采样值通过数据分类器T进行分类，将各变量的监测值按偏离标准值的不同程度分类到相应的作用域内，构成数据分类矩阵Q。

定义5数据分类器T。由系统各变量的标准值和各等级异常偏离度值所构成的矩阵，称其为数据分类器T，

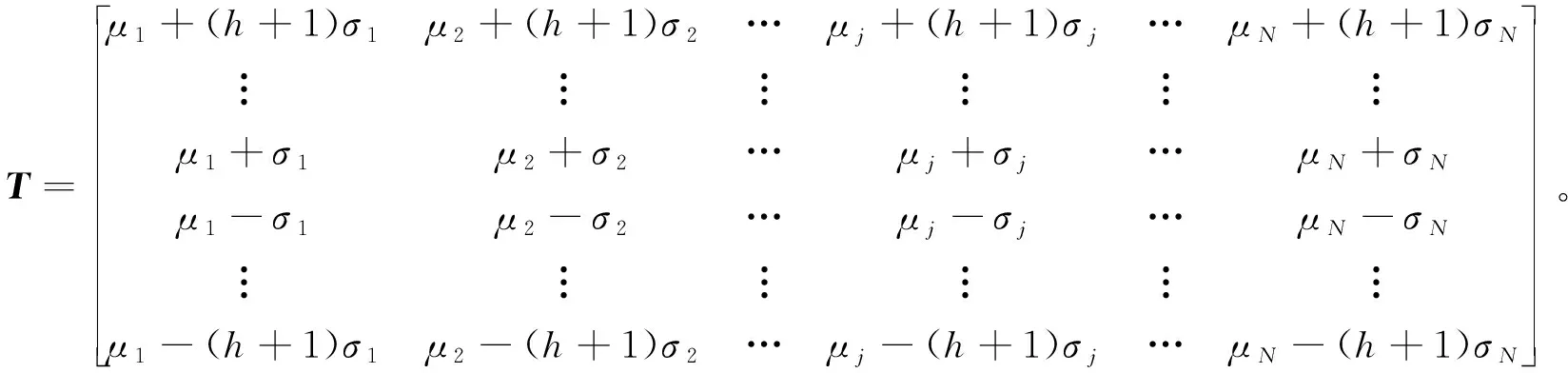
(5)

该数据分类器的主要特点是将难以辨识的浮点型数据以简单的整型数值代替并进行分类，对变量j监测数据的分类过程如式(6)所示:

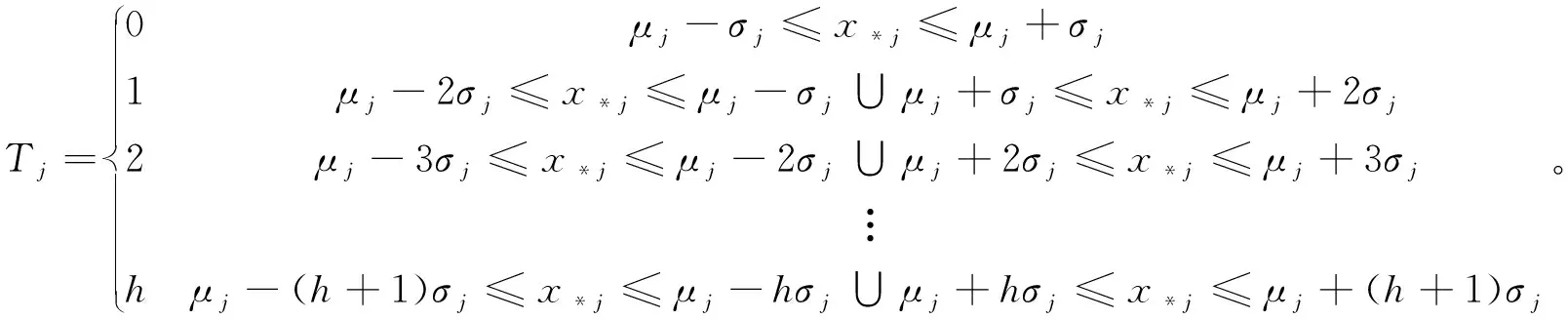
(6)

2.2 分类矩阵Q

定义6分类矩阵Q。 将待测的监测数据通过数据分类器T进行分类后，所得到的整数型矩阵称为数据分类矩阵Q，

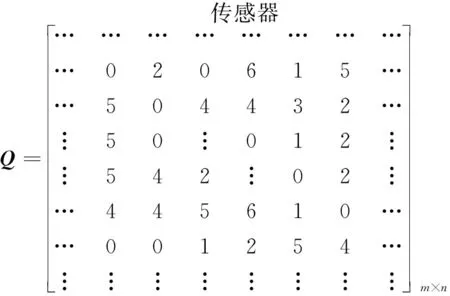
(7)

分类矩阵中不同元素代表不同的系统运行状态。根据三西格玛质量控制原理，当异常值在0～2之间时，说明系统处于安全运行状态范围内。当异常值高于正常运行范围时，异常值越高，则系统异常程度越高。

3 系统状态特征谱

虽然人眼难以直观地辨识出整型数据的变化规律，并从中找出异常数据，但是人眼对色彩变化的敏感度远远高于对数字变化的敏感度。通过制定着色规则，对分类矩阵Q中的元素进行着色，构造系统状态特征谱。

3.1 状态特征谱的着色规则

根据RGB色彩规则，对DCS监控数据集中所有数据按照偏离最优值的程度进行细分。为了人眼有效地区分色彩，三原色RGB的各个分量只能在全0和全1中取，其中RGB三个分量取0和1为色彩的两个极端情况，本文选择23= 8种最极端的颜色表示系统运行健康状态。孙锴等[3]在构造系统故障图谱研究中，用黑色表示故障点，白色表示无故障数据。对数据矩阵X着色后，以二值数字图像的形式展示系统运行健康状态。为了与黑白二值系统故障图谱相区别，同时由于在彩色图像中，人眼对红色的辨识度高于黑色，视觉感官更强，本文用红色代替黑色表示系统变量观测值偏离最优值最远的区间，用绿色代表观测值处于最优区间，中间过渡色根据偏离最优值距离区间从近到远依次着色为黄、白、蓝、青、紫。将蕴含复杂机电系统运行健康状态的数据矩阵X从海量高维Hausdorff空间投影到二维色彩相空间中，构造出系统状态特征谱。

定义7状态特征谱P。对数据分类矩阵Q进行染色，其中pixel_0表示为绿色、pixel_1表示为黄色、pixel_2表示为白色、pixel_3表示为蓝色、pixel_4表示为青色、pixel_5表示为紫色、pixel_6表示为红色，在二维平面中可以得到彩色图像，称为状态特征谱P，如式(8)所示：

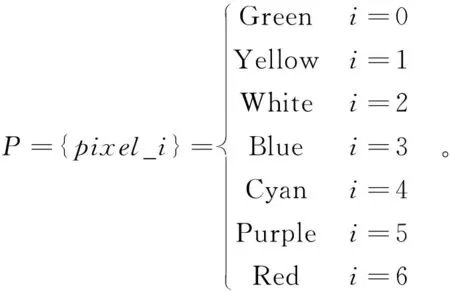
(8)

依据式(8)所定义的着色规则，对数据分类矩阵中的数据进行着色，系统整体的运行健康状态通过色彩的分布和变化被呈现在一幅二维平面数字彩色图像上。

3.2 构造流程

系统状态特征谱的构造流程如图2所示。根据现场监控记录，挑选出系统运行状态最佳的一天所对应的DCS数据集作为运行状态的分析标准。将待测DCS数据集以同样的采样周期为单位划分为的独立数据集。通过构建数据分类器T、分类矩阵Q，构造系统特征谱P，分析系统运行健康状态。具体步骤如下：

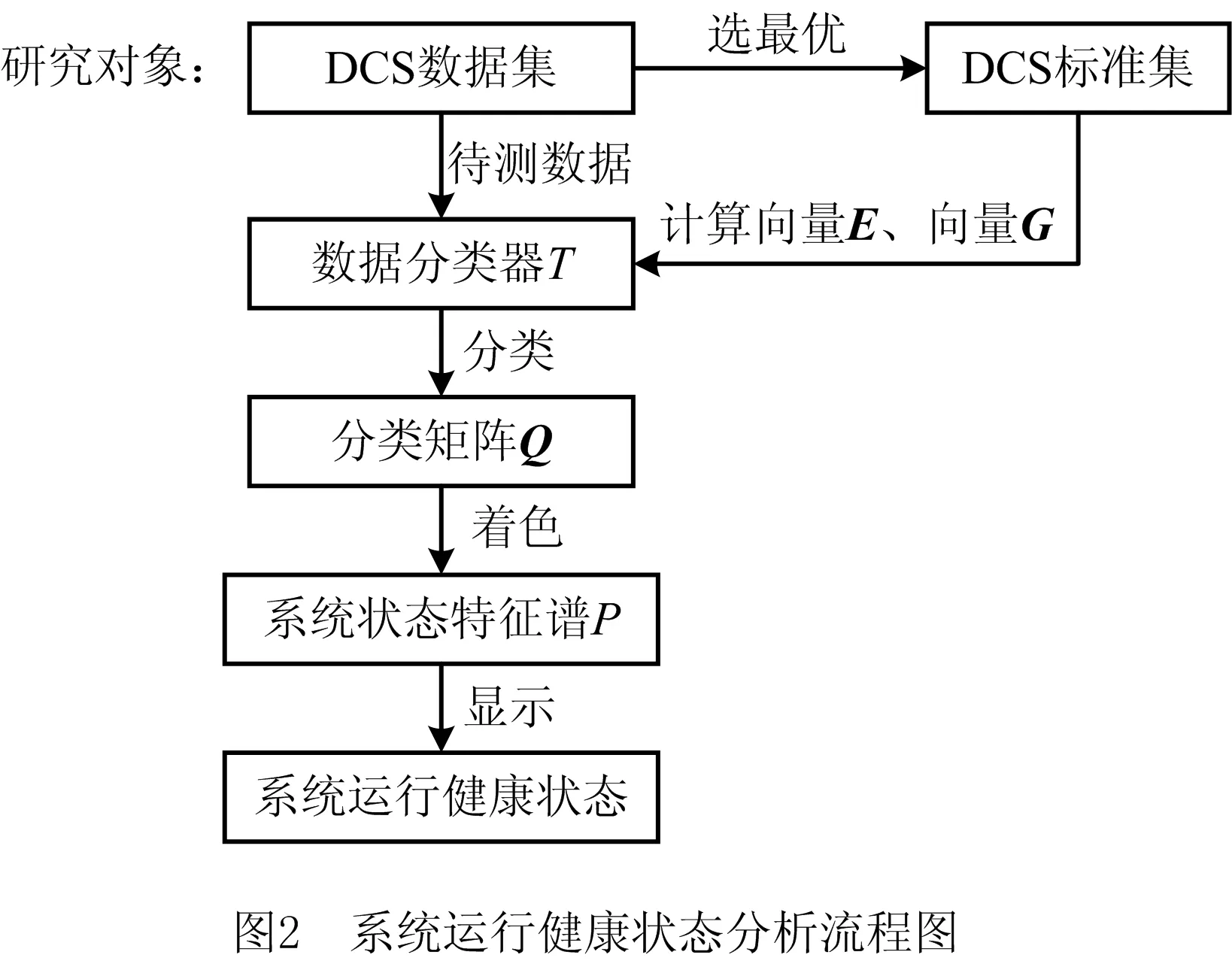
步骤1根据现场监控待测的DCS数据中，人为选取出某段系统运行状态时段最佳的DCS监测数据集，作为标准集。

步骤2对DCS标准数据集求取最优监测值向量和异常偏离度向量，构造数据分类器T。

步骤3将待测的DCS数据集通过数据分类器T进行分类，根据不同程度偏离最优标准值进行分类后，构建出分类矩阵Q。

步骤4按照数据着色规则对分类矩阵Q进行着色，构造系统状态特征谱P。

步骤5根据分析所构造的系统状态特征谱，分析系统运行健康状态。

4 算法的先进性和有效性

田纳西-伊斯曼过程仿真过程(Tennessee-Eastman Process，TEP)是由伊斯曼化工公司提出的一种通用化学过程模拟器，是一个用微分方程模拟化工生产过程的仿真系统，其主要目的是为了给评估监测方法和工程控制提供一个现实的工业流程仿真。

田纳西-伊斯曼过程主要由反应器、压缩机、冷凝器、分离器和汽提塔5个单元组成，包含了 A、B、…、H8种成分，其主要工艺流程如图3所示。图3中XA, XB，…，XH为输出；1、2、…、13为流号；CWR为冷却水回流；CWS为水煤浆；LI、JI、TI、FI和PI为变量控制器。反应器的物质流经过冷凝器冷却后，送入分离器中进行分离，将分离出来的蒸汽经过压缩机压缩后再循环送进反应器中。

TEP包含可以模拟正常运行状态的52个变量，其中XMEAS(1)～XMEAS(41)为监测变量，XMV(1)～XMV(12)为控制变量，所有变量同步采样周期为1 min。并且TEP测试数据集包含1个无故障数据包和21个典型类型的故障数据包，每个数据包包括480×52个数据点。

传统的数据驱动故障辨识方法主要包含PCA, 规范变量分析(Canonical Variable Analysis, CVA) 和动态主元分析(Dynamic Principal Component Analysis, DPCA)，这些方法的主要思想是基于数据降维。利用本文所提出的方法与传统数据驱动故障辨识的方法对田纳西仿真系统的21种典型故障的数据进行分析，各方法的故障辨识精确度情况对比如表1所示。

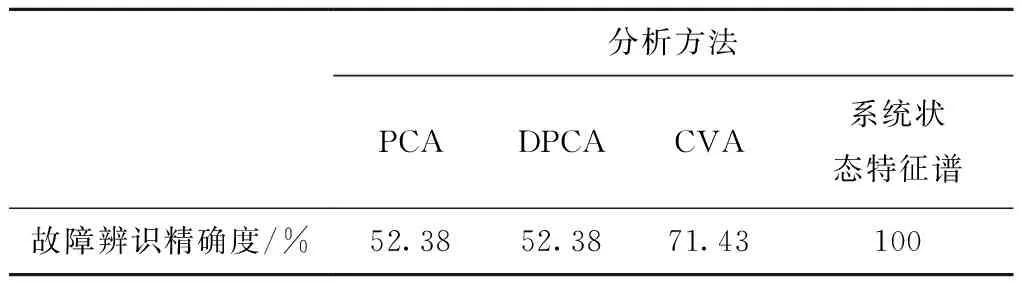
表1 状态特征谱方法与传统方法的对比

由表1可知，PCA和DPCA方法对于21种典型故障模式的故障识别精确度为52.38%，CVA方法的故障识别精确度为71.43%，而本文提出系统状态特征谱方法的故障识别精确度为100%。通过对比，本文所提出的系统状态特征谱的方法对故障的识别精确度更高。

根据定义1可知，将52个监测变量所构成的时间序列作为列向量，按照XMEAS(1)～XMEAS(41)、XMV(1)～XMV(11)的顺序排列，构造了480×52的二维矩阵。根据图2的系统状态特征谱的流程，构造出TEP有无故障状态特征谱，对比无故障系统故障图谱和有故障系统状态特征谱，如图4所示。

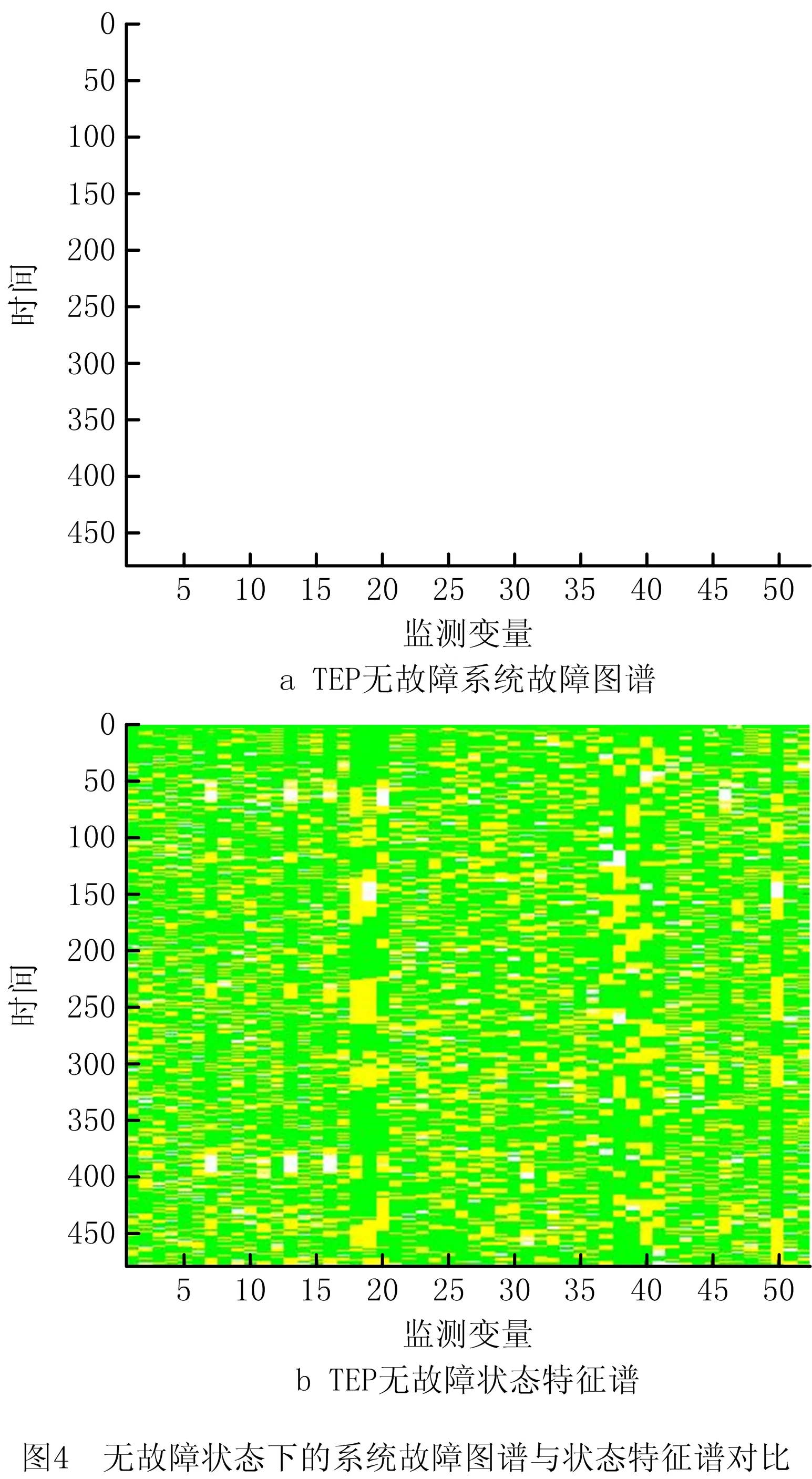
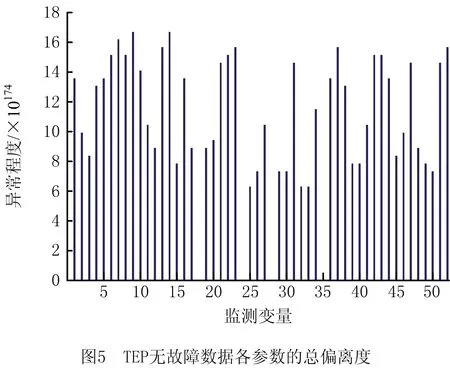
从图4a可以看出，无故障状态下的系统故障图谱是一副纯白色的图像，只能反映系统设备都正常运行，更多的信息无法被呈现出来。而如图4b所示，本文所提出构造系统状态特征谱的方法在无故障状态下呈现出绿、黄、白色彩相间的一副图像，显示了系统中各个设备在安全范围内波动的情况。这虽然表明监测数据还在正常运行的范围内，但偏离最优值程度各有不同，被呈现出来的信息更加具体丰富。根据本文提出的分类矩阵的概念，将TEP无故障数据构成的分类矩阵中的各列进行求和，各参数的异常程度值如图5所示。将监测值异常程度由高到低进行排序，需要着重观察并予以关注的变量序列一目了然，然而这些信息在图4a的故障图谱中均被抛弃掉了，导致无法具体地呈现系统运行健康状态。

以TEP故障模式4为例，对比系统故障图谱[3]与系统状态特征谱绘制出的系统有故障图谱，如图6所示。

从图6a中可以看到，变量51处有一条纵穿图谱的黑色条纹和其他零星分布的黑色斑点，这表明变量51在整个采样周期中都出现了异常，其他变量的监测值零星出现异常，但很快消失。由于整个图谱上的异常值都用黑色表示，无法区分变量51出现的异常值和其它变量显示的异常值的异常程度及区别，无法判定出着重观察的区域。

由图6b可知，TEP状态特征谱是由不同颜色所构成的。图6b中，变量51是一条贯穿整个监测时序的纵向红色条纹，红色像素代表了系统目前已经发出了严重故障的预警。而在其他位置出现部分蓝色、青色、紫色斑点，这些不同的色彩代表着不同的故障程度，但它们的异常严重程度远远小于变量51“反应器冷却水流量”出现的严重故障。根据图6b给出的信息，工程师可以判断出其他系统变量造成的故障程度处于安全范围内，仅予以观察，但不采取措施，而是专注解决变量51造成的故障，这一信息无法从图6a中获取到。

相比于系统故障图谱而言，本文提出构造系统状态特征谱的方法不仅能够表达出系统是否处于异常状态的信息，同时通过细化系统故障的映射关系，不同的颜色代表系统不同的异常程度，根据像素点的位置来判断系统异常情况并采取相应措施，从全局上更准确地把握了系统的运行状态。

5 某化工企业空气压缩机组实例应用

某化工厂空气压缩机组的设备连接如图7所示。该压缩机机组由汽轮机、空压机、增压机、变速箱等设备组成，设备与设备之间通过连接管进行连接，各设备间相互协调，达到空气压缩的功能，是一个典型的复杂机电系统。该化工厂空气压缩机组总共包括250个传感器，种类繁多，如温度、流量、压力、转速、功率等传感器。这些传感器对系统进行实时监控，实时将监测数据上传给控制系统——DCS。

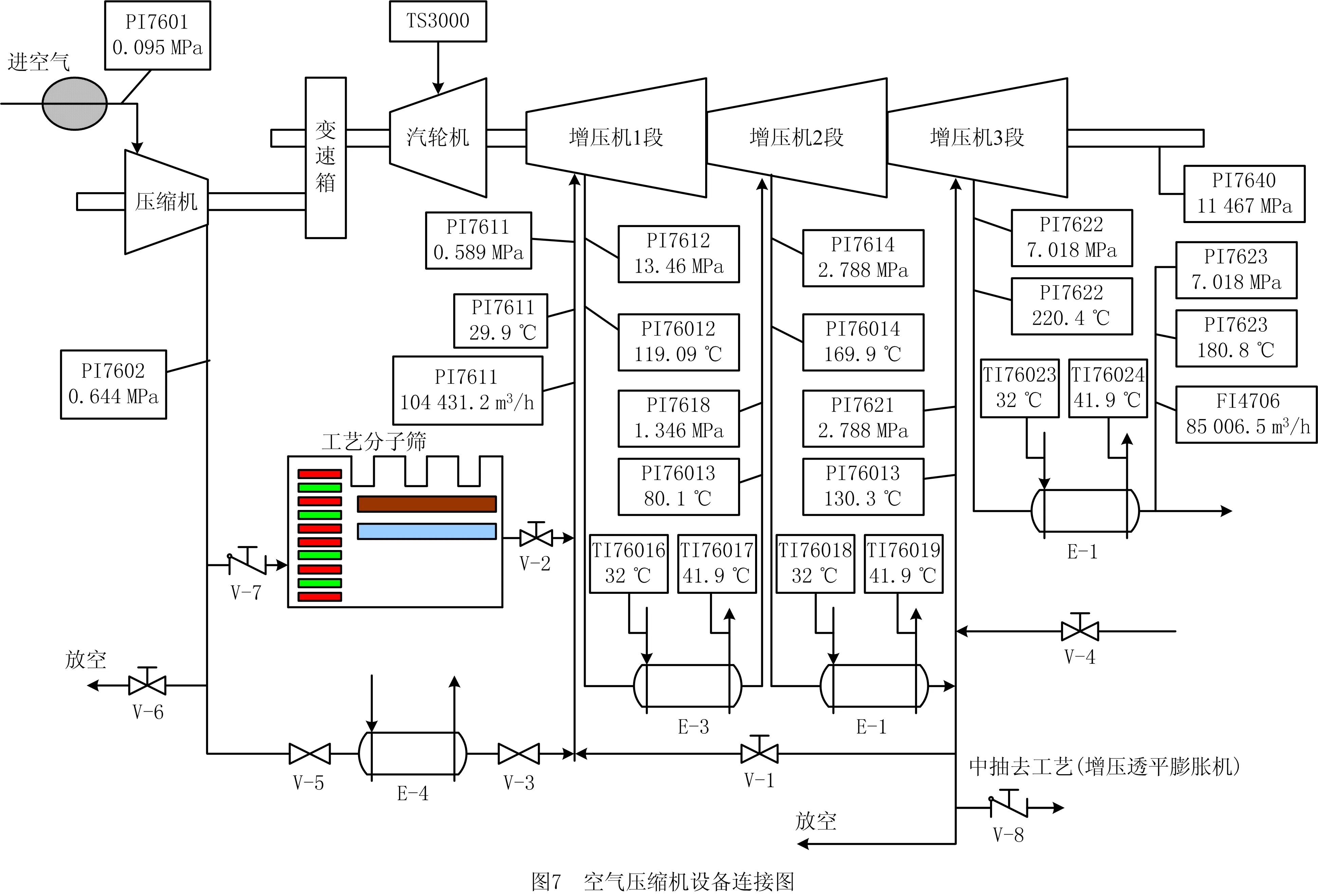
对该空气压缩机组运行半年时间的监测数据进行分析。根据定义2～定义7，将该空气压缩机组2013年上半年所有的DCS监测数据构造出反映半年内系统运行健康状态的状态特征谱，如图8所示。其中横轴表示250个系统采样参数变量，纵轴表示系统的采样时序为721，监测数据的测试样本数为32 805 500个数据点。

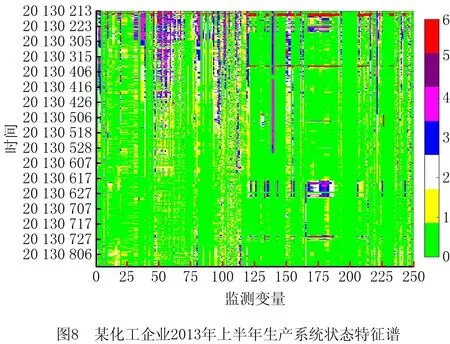
由图8可知，该化工企业2013年上半年的系统状态图谱上分布着不同色彩的像素点。根据本文所提出的数据分类算法以及着色规则可知，图8中呈现的绿、黄、白3种颜色代表系统处于正常运行状态。其中绿色为最佳的系统运行状态，黄色和白色代表在系统允许的波动范围下正常运行，但实际上已经说明系统处于亚健康状态了，应给予留意和观察；而绿、黄、白以外的其他颜色分别代表着不同程度的故障运行状态，其中红色为严重故障状态。如图8所示，有两条较为醒目的红色条纹横穿整幅图谱，它们分别代表2013年02月14日、2013年03月25日这两天的系统运行状态。2月14日的红色条纹是横向贯穿整幅状态图谱的，说明当天所有的传感器监测的设备都在发出严重故障预警；03月25日的红色条纹代表传感器120～250所监测的设备都在发出严重预警，此时必须要采取相应的检修措施，整个系统应该立即停车大修。因此，本文对图8中较为明显的两条红色条纹及前后时段作为重点进行放大分析，如图9和图10所示。

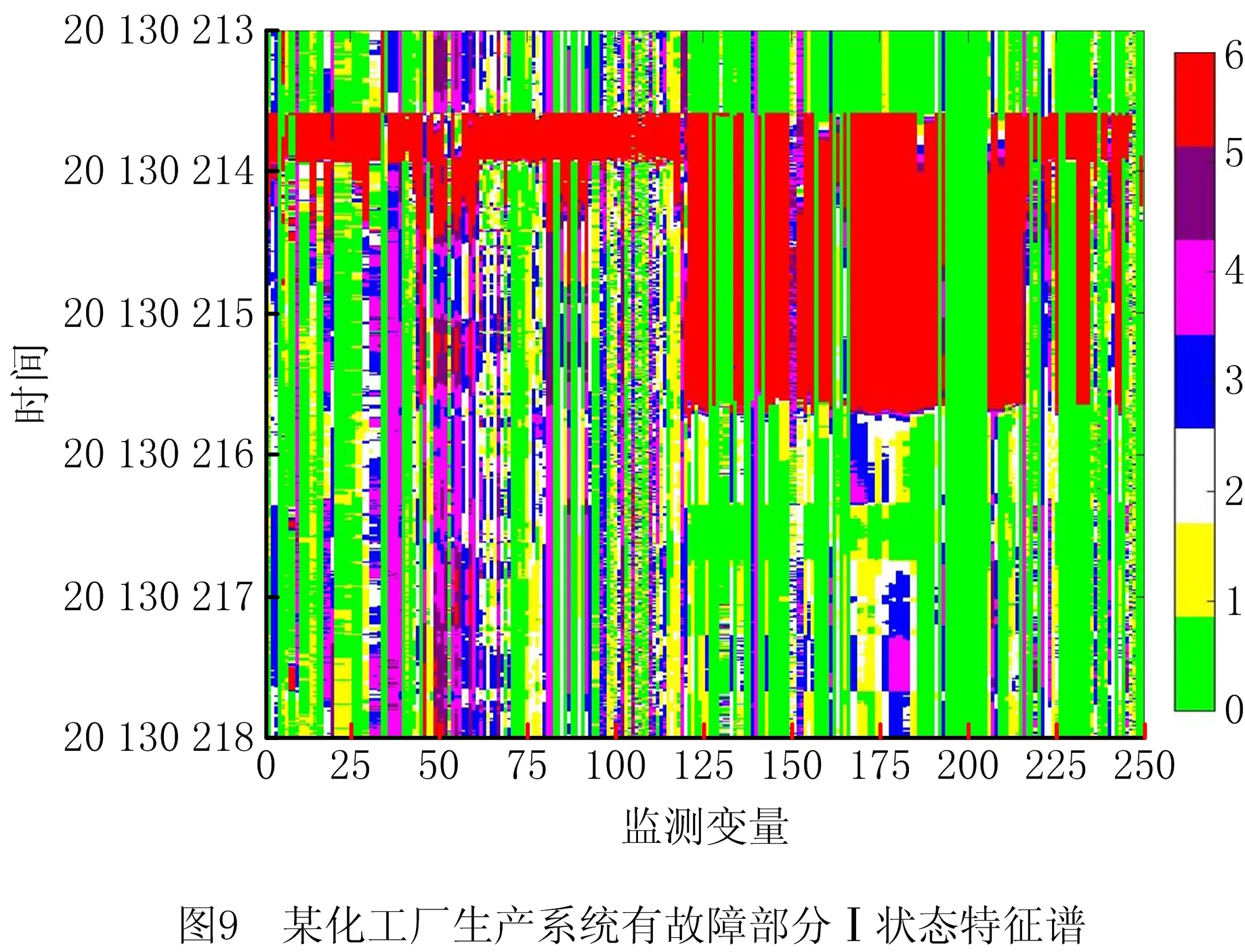
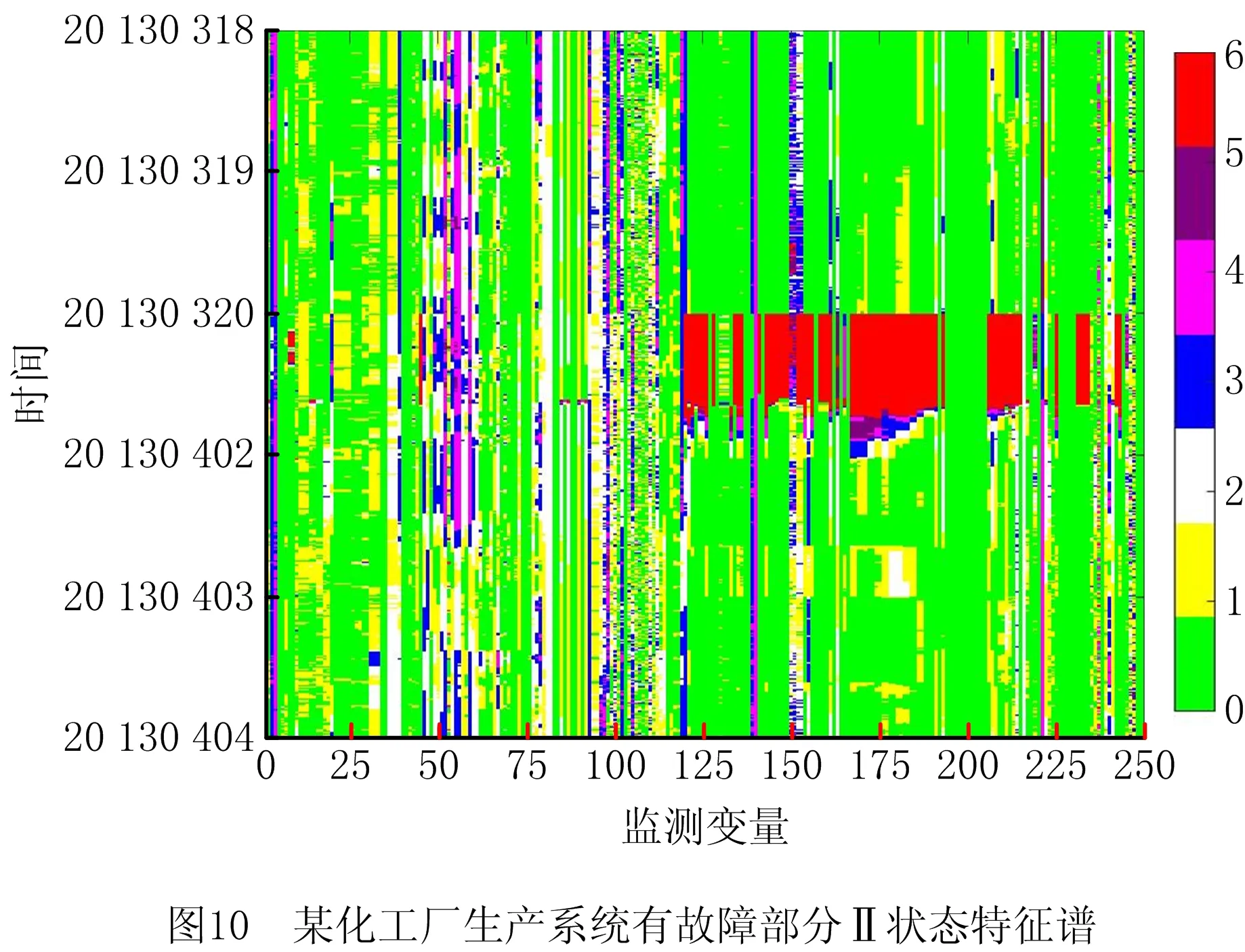
图9中，在2013年2月13日中午12：00左右至14日零点左右，整个系统状态特征谱的色彩呈红色，且基本贯穿了250个系统监测变量，这说明整个系统都在发出严重故障预警。2月14日零点～2月16日下午13：00左右，系统变量为177～195、变量210～248左右的采样点仍持续发出严重故障预警。变量为35～68在系统状态特征谱的整个时序上贯穿着紫色和蓝色，代表着不同程度的故障发生，但这些异常程度不高，可将这部分时段呈现出来的系统运行状态与实际工况相结合，对此时段的系统运行状况予以关注或采取相应措施。

如图10所示，传感器120～190、210～240在2013年3月20日～4月1日范围内呈现着红色斑点，代表在这段时序范围内，这些系统变量发出严重故障预警。并且图10中的部分变量在一定的时序范围内呈现紫色像素和蓝色像素，而这些色彩同样也反映着各系统变量不同程度的故障状态，这些部分将作为重点观察区域，观察系统故障运行状态是否有向严重故障运行状态的趋势。因此，本文提出的方法是通过观察系统状态特征谱颜色的变化及分布规律，全面地把握系统运行健康状态，在重大安全事故发生之前准确快速地作出预警，避免不必要的损失。

6 结束语

本文提出一种基于DCS监测数据集构造系统状态特征谱分析系统整体运行健康状态的方法。该方法改进了之前提出的系统故障图谱无法精确反映故障程度的缺点，通过设计数据分类器和制定着色规则，对系统监测数据集中的数据进行分类和着色，将所有的数据呈现在二维图像上，构造出信息丰富细致的系统状态特征谱。通过分析像素点的位置以及颜色的分布范围，实现具体全面的掌握系统的运行健康状态，提高了分析准确度，为之后的量化分析奠定了基础。下一步的研究将利用数字图像处理技术中丰富的图像分析算法，更加充分地挖掘潜藏在系统状态特征谱中的系统健康运行状态，实现复杂机电系统运行健康状态的量化评级和快速、准确溯源。