股票投资组合分析——基于均值- 方差模型

周廷森

（贵州大学经济学院，贵阳 550025）

引言

中国资本市场经过30 多年的发展，已经由初期单一的市场结构向多元化市场发展，形成了多层次的资本市场并逐步走向成熟。近年来，中国A 股市场投资者结构正在发生着明显改变，机构投资者占比越来越高。根据中国证券投资基金业协会数据显示，截至2021 年1 月15 日，A 股流通市值的18.44%由境内专业机构持有，处于近年来的峰值。中国资本市场正向投融资并重的格局发展演变，其财富管理功能越加凸显。中国市场对外开放程度逐步提升，分别于2014 年、2016 年和2019年开通沪港通、深港通和沪伦通，市场交易品种不断丰富，交易机制更加完善。在发行制度上，我国正在推进核准制向注册制的转变，上市公司退市制度不断完善。相关法律和监管制度也不断完善，对公司治理的监管由法律和机构的单一监管转向法律制度、监管机构和广大投资者组成的多层次监管格局。在这样的大背景下，我国资本市场为投资者提供了一片“沃土”，股票收益表现回归到基于公司基本面的价值体现。从投资者的视角看，我国国民的金融素养在不断提高，股票作为一种重要的投资品种被广大个人投资者所接受并纳入资产配置的范畴。波动是股票市场最显著的特点之一，普通投资者如何在波动中以风险与收益的最佳平衡为前提获取超额收益是其最关心的问题之一。

基于以上背景，对旨在获取超额收益的个人投资者来说，具备择股择时等专业能力就显得非常重要。投资组合理论是结合投资者风险偏好与对收益的预期基础上最优化投资绩效的方法。构建合适的股票投资组合能帮助投资者在资本市场找到收益优异且风险较小的机会。本文通过主成分分析，从沪深300 成分股中选取投资标的组建股票池，通过均值方差模型构建投资组合。对于普通投资者来说，本文梳理的方法在操作上具有一定的参考意义。

一、文献综述

在Markowitz 创建现代投资组合理论之前，学术界对于资产风险与收益的研究更多是定性研究，对风险的量化分析以及风险与收益之间量化关系的研究没有找到合适的方法。1952 年美国著名经济学家Markowitz（1952）将数理统计方法引用到投资组合选择的研究中，首次从风险和收益的量化关系角度详细分析最优资产组合的选择问题，提出著名的均值- 方差模型。此后，围绕着投资组合的研究不断出现，学界运用新的方法和技术手段，结合现代经济的运行规律和大量数据，不断获得新的研究发现。Markowitz 提出的均值- 方差模型有严格的假定条件，并且模型计算较为复杂，在实践中，投资者无法做到按照假设条件限定的条件去操作，也无法忽略一些其他的约束条件，比如持有资金量、市场利率、最小交易单位、交易费用等。William Sharpe（1963）建立了一种均值- 方差模型的简化式，提高了现代证券投资组合的实用性和可操作性。Hiroshi Konno和Hiroshi Yamazaki（1991）在风险度量上用绝对离差替代方差，进一步提高了均值- 方差模型在应用上的可操作性。在无风险资产借贷方面，Black 研究了无风险资产借贷条件下的资产定价。经典均值- 方差模型的假定条件中假设投资资产是无限可分的，这与实际不符。Jobst 等（1996）利用启发方式算法计算有基数限制和交易份额限制的均值- 方差模型。Mansini 等（1999）也用相同方法研究了含最低交易单位的股票投资组合问题。

我国国内资本市场虽然起步较晚，但是发展迅速，相关学术研究也取得很多结合我国实际情况的新成果。苏咪咪和叶中行（2005）讨论了在协方差矩阵奇异时如何求解投资组合的最优解。孙超和李胜宏（2008）在求解最佳投资组合解的过程中加入了交易成本和交易约束两个条件，最终计算结果表明交易成本这一因子对组合构造的影响。宋立军和杨永愉（2008）结合我国股票市场不允许做空的特点，讨论了均值- 条件风险价值模型的求解问题。高建伟和边念怡（2009）从动态的角度出发，基于最坏情形条件风险价值对风险进行控制，将风险控制应用到整个投资过程，并且给出了相应的优化模型和求解，最后结合实证数据论证了优化模型的有效性。王晓琴和高岳林（2020）在交易成本约束和投资权重约束两个条件下研究了多阶段的投资组合构造，并建立了对应优化模型。莫东序和郑田丹（2021）从方法优化的角度对传统的均值方差模型做了优化研究，其模型构造中基于复杂网络的局部聚类系数法在实证中显示了良好的应用效果。

综上所述，学术界围绕投资组合的风险及收益的度量以及两者之间的量化关系做了大量研究。Markowitz首次提出了经典的均值方差模型，在该模型的基础上，学界针对其理论的局限性又进一步提出了新的解决方法。本文基于中国的A 股市场，利用主成分分析的方法分析各公司的财务指标，选出合格标的构成股票集合，基于均值方差模型确定最佳投资比例，最后对组合绩效进行评估，以期为投资者择股和组合构造提供参考意义。

二、样本股选取

（一）选择指标

企业的各项财务指标是其经营管理的晴雨表，体现了其经营成果、财务状况和现金流量状况。为了较为全面地反映公司的运营状况，本文选取2019 年第四季度上市公司的51 个财务指标作为分析对象，其中，短期偿债能力指标如流动比率、速动比率、每股现金流量净额等，长期偿债能力指标如资产负债率、产权比率、权益乘数、利息保障倍数等，营运能力指标如存货周转天数、应收账款周转天数等，盈利能力指标如营业净利率、总资产净利率、权益净利率等，估值指标如每股收益、每股净资产、每股营业收入等。

因为指标众多且某些项彼此存在相关关系，所以首先利用主成分分析对分类结果做降维处理，使得新生成的维度指标能够较好地代表原来指标，以便于后续投资组合构造分析。

（二）聚类分析

运用聚类方法可以发现数据项目间的信息依赖关系，从而去除或者合并有密切依赖关系的数据项，以对复杂结构的多维数据进行聚集，是数据预处理阶段比较有效的方法之一。

财务指标数据众多，且财务指标间可能存在某些相似特征，因此，首先通过聚类分析对指标做聚类处理，拟分为K类。通过python 调用scikit-learn 实现K-means聚类分析模型训练和参数计算。根据算出的轮廓系数值，当K=5 时，轮廓系数最大为0.24；另外，根据Calinski-Harabasz准则算出的Calinski-Harabasz 指数在K=5时，最大为36.54，因此将财务指标分为5 类。

（三）主成分分析

PCA 的原理是对数据的众多指标维度进行降维处理，将多维指标信息转化为较少的几个综合指标的统计方法，其前提是降维后的指标应很好的代表原始数据的特征，具体步骤如下。

第一步，数据标准化处理。为了有效化解不同指标因度量单位带来的数量等级差异，首先利用标准差标准化方法对财务指标数据进行标准化处理。标准化公式如下：

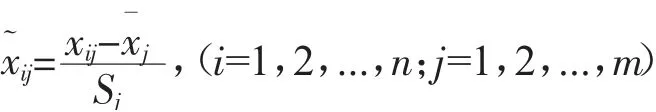
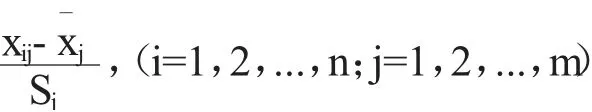
第二步，计算主成分对象。通过python 中的PCA函数产生15 个主成分模型对象。

第三步，计算方差贡献率。15 个主成分的累计贡献率为89.56%，能较好解释总体方差。

第四步，计算主成分载荷，本文也通过调用python函数计算完成。

第五步，计算主成分得分，并按照聚类分析的结果每簇取得分最优的两支股票，再按照各主成分的方差贡献率进行加权平均，将计算出的各股票对应的企业得分进行降序排列，取排名前十的公司构建股票集合，如表1 所示。

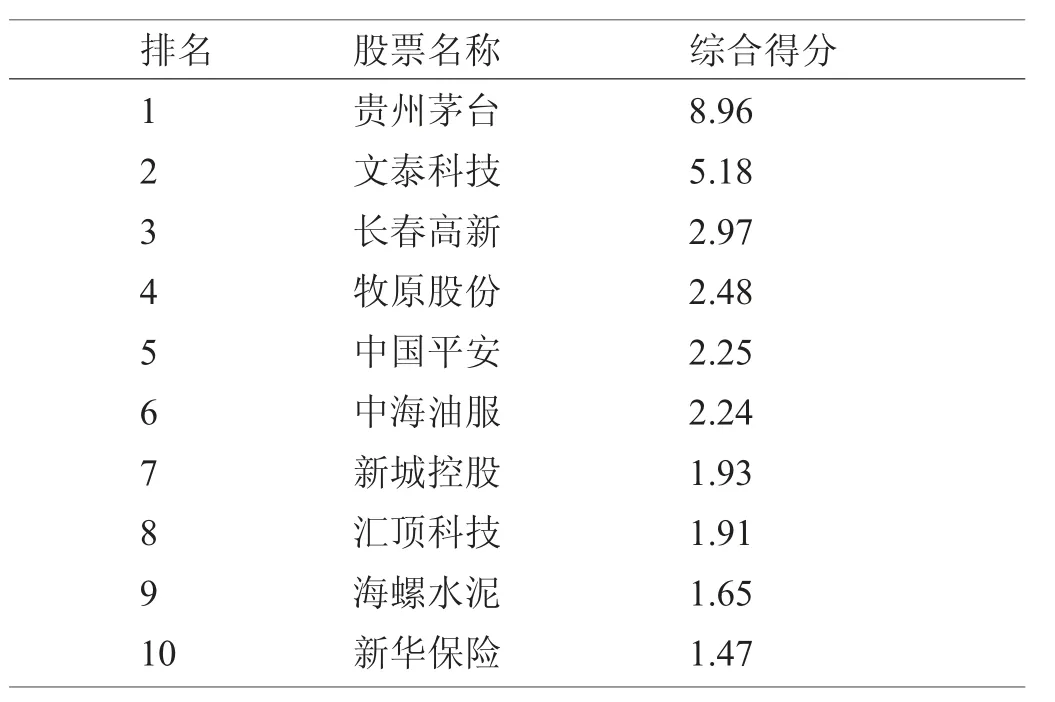
表1 前10 名上市公司综合得分排名表

三、投资组合构造

（一）均值- 方差模型概述

Markowitz 首创的现代投资组合选择理论的基本原理是：证券收益用证券的期望收益衡量，证券的风险由证券收益的方差衡量，各支证券预期收益的加权平均来表示整个组合的收益，即如下模型：

其中，r为第i 支证券的预期收益，r为证券组合的收益，ω、ω分别为第i、j 支证券在证券组合中的权重，σ（r）为证券组合收益的方差，σ为证券之间的协方差。该模型的实际意义是在一定风险程度下求解出最优收益的证券组合，也可在组合期望收益一定的条件下得到单项资产的最佳投资权重，以使整个组合的风险最小化。

（二）股票投资组合构造

构建股票投资组合的意义在于结合投资者自身风险偏好和对收益的期望，找到一个最优的投资组合结构。选取上述主成分分析选出的10 支股票在2018年10 月至2021 年3 月的日收盘价数据计算日收益率，公式为：

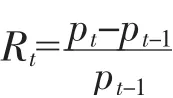
R为股票在t 日的收益率，p为股票在t 日的收盘价，p为股票在t-1日的收盘价。

分别求解组合中单支股票的日收益率均值、收益的方差、标准差。模型中预期收益是投资者设定的预期收益值，这里用组合中单支证券在所选期间内年化收益率的算术平均值表示，计算可得预期收益率约为0.31。由均值- 方差理论，定义如下目标函数：

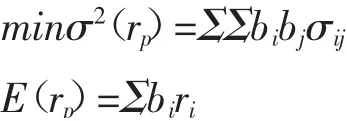
设定条件：Σb=1，b≥0即允许卖空，r为投资组合的收益，r为第i 支股票的收益，b、b分别为第i、j 支股票在资产组合中的权重，σ（r）为组合收益的方差，σ为两支股票的协方差。通过调用python 的相关函数计算得到最优解：b=0.284，b=0.011，b=0.027，b=0.048，b=0.229，b=0.01，b=0.048，b=0.057，b=0.284，b=0。根据求解的最优解，投资者若要达到预期收益，且在该预期收益下组合风险最小，应将资金的28.4%、1.1%、2.7%、4.8%、22.9%、1%、4.8%、5.7%、28.4%、0 分别投资于贵州茅台、闻泰科技、长春高新、牧原股份、中国平安、中海油服、新城控股、汇顶科技、海螺水泥、新华保险。

四、投资组合评价

（一）夏普比率

Sharpe 基于Markowitz 现代投资组合理论，提出衡量基金业绩的风险调整指标：夏普比率。夏普比率的核心思想是假设理性投资人会投资并持有一个最有利于自己的投资组合，即风险水平一定但预期收益最大化或预期收益一定风险水平最小化的投资组合（叶志强，张顺明，等，2010），其计算公式为：

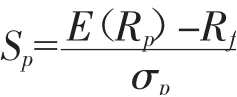
其中，S为夏普比率，E（R）为组合的期望收益率，R为无风险收益率，σ为资产组合的标准差。投资组合的预期收益率及标准差分别由组合中单支股票年化收益率的简单算术平均值和组合收益的标准差表示，计算可得R=0.31，σ=0.30，无风险利率采用2018 年10月22 日—2021 年3 月31 日期间中国十年期国债收益率收盘价的均值0.031 3 表示，通过计算可得S=0.929。同样的方法可以计算出沪深300 指数的S=0.91，根据夏普比率的含义，投资组合每承担1%的风险，组合回报率增加0.929%，可见该投资组合的表现较好。

（二）特雷诺比率

特雷诺比率（Treynor Ratio），该指标的分子为组合的期望收益与无风险收益率的差值，分母则是投资组合的贝塔值，表示当投资组合每承受一单位系统性风险时所产生的风险溢价。其公式为：

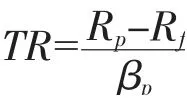
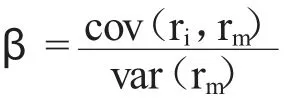
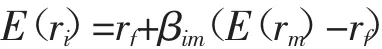
其中，E（r）为投资组合的期望收益，r为无风险利率，β为股票i 的β 系数，E（r）为市场组合的期望收益。通过最小二乘法估计投资组合的β系数约为0.93，继续可算出TR=0.268 7。特雷诺比率比较的基准是市场组合收益率与无风险资产收益率的差值，即γ=r-r，可算出γ=0.189 7。因为TR＞γ，表明投资组合承担单位市场风险所取得的收益优于大盘表现。