一种顾及几何精度因子的GNSS控制网构型选站方法
顾嘉琛,田坤俊,宋传峰
( 1. 山东无形信息技术有限公司, 山东 泰安 271000;2. 武汉大学 测绘学院, 武汉 430079;3. 武汉大学卫星导航定位技术研究中心, 武汉 430079 )
0 引 言
北斗卫星导航系统(BDS)是我国自主建设运行的全球卫星导航系统(GNSS),可为全球用户提供全天候、全天时、高精度的定位、导航和授时(PNT)服务的国家重要时空基础设施[1-2]. 2020年7月31日,北斗三号卫星导航系统(BDS-3)正式开通,标志着北斗“三步走”发展战略圆满完成,北斗迈进全球服务新时代. 随着BDS-2/BDS-3的迅速发展,空间大地测量、地壳运动监测、大陆板块运动监测、GNSS气象学、工程测量、水文大地测量等都对BDS数据处理提出了更高的精度要求,如何获得高精度基线结果以及提高基线解算效率依然是当前面临的重要问题[3-5].
在大地测量领域中,几何精度因子(GDOP)值是评估解算性能的重要指标之一,GDOP是在实际利用最小二乘平差解算过程中的权逆阵对角 线上的重要组成部分,能够反映出观测信息对于解算的未知参数的贡献程度. YARLAGADDA R等[6]对GDOP矩阵进行了详细的推导和分析,李建文等[7]利用导航卫星进行求解GDOP值最小值的实验. 但近年来,有学者在基线解算过程中对GDOP值进行分析和计算. 研究GNSS相对定位过程中GDOP值对控制网构型影响具有一定的参考意义和价值. 在基线相对定位解算中,测站的数量与构成的基线数量成正比,基准站数量增加,所求得的待测站点位精度也随之提高. 但由于测站数量的增多,基线数量也成指数型增长,这使得整个网形的计算效率也会大大降低,因此在精度保持较高的情况下提高基线解算效率,在保持解算效率的情况下提高解算精度很有必要. 本文以定位观测方程的GDOP最小值为准则,计算出一种基准站与待测站之间的最小GDOP值组合,进行相对定位基线解算,并与传统的格网法选站的解算结果进行对比,同时通过数据实验验证此选站方法的可行性.
1 选站模型
1.1 顾及 GDOP值选站法
在进行相对定位基线解算时,观测方程为

对观测方程进行线性化得

式中: Δ ρ 为线性化后的观测方程余项;A为线性化系数矩阵,考虑到接收机钟差作为待估参数求出,为了方便计算,A矩 阵第四列设为-1;为参数估计向量;L为常数项. 其中系数矩阵A具体可用下列矩阵进行表示:

式中:xi,yi,zi为待测站的三维坐标,xj,yj,zj为基准站的三维点坐标,为待测站和基准站之间的几何距离.

当独立等精度观测时,P为单位权阵,假设各观测量具有相同的距离测量中误差 σ2,则定位误差的协方差阵为

由式可得, (ATA)-1为测站测量误差转换到测站位置误差的变换因子矩阵. 根据导航定位中GDOP值得定义
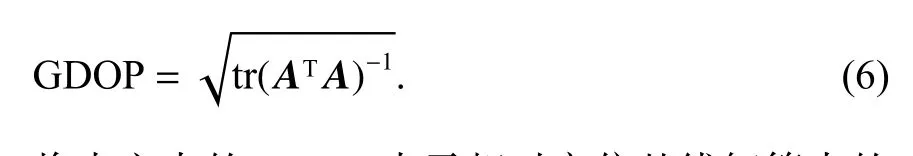
将本文中的GDOP表示相对定位基线解算中的基准站与待测站之间的精度衰减因子,其数值大小可以体现出所有测站的几何位置分布对最终的定位误差的影响程度. 因此在基线解算前计算出GDOP值最小时基准站与待测站的几何位置分布,将会提高待测站最终的解算精度[7-8].
1.2 格网化选站法
由于地面观测站有区域性分别不均的特点,以国际GNSS服务(IGS)站、MGEX站为例,地面观测站在亚欧大陆较多,其他大陆较少;陆地较多,海洋较少[9-10]. 因此为了避免所选测站集中在某一区域,需对测站位置进行整体控制,从而提高整个控制网解算的精度. 以经纬度进行格网化选站的个数用N来表示.
2 实验分析
2.1 实验设计与处理策略
考虑到数据质量对解算精度的影响,本文实验算例选取全球18个iGMAS观测站作为待测站,以原始观测文件表头概略坐标作为测站起算坐标进行研究[11].基准站选用能够接收到BDS信号的MGEX站,考虑到观测站接收到的数据质量,观测站之间满足长基线要求,观测站稳定性等方面,从全球500多个MGEX站筛选出满足要求的测站,共计137个. 对其进行顾及GDOP值选站和格网化选站,结合待测站的个数,本次实验采用两种方法选择出6个基准站进行实验.
目前BDS已发展到第三代,地面观测站观测到的BDS卫星数量逐渐增多. 图1给出了iGMAS地面观测站WHU1站在2020年100天观测到的各系统BDS卫星可见数. 图2给出了当天利用WHU1站观测数据计算出的各系统BDS卫星位置精度因子(PDOP)值. 可以看出单BDS-2卫星可见数约在11颗,PDOP值基本约稳定在2.4;单BDS-3卫星可见数约在6颗,PDOP值约在4.4;个别历元由于BDS-3卫星数观测数量较少,PDOP值达到10以上;而所有BDS卫星加起来后卫星可见数约在17颗,PDOP值约稳定在1.5,表现较好. 因此本实验采用BDS-2/BDS-3卫星的观测数据进行解算.
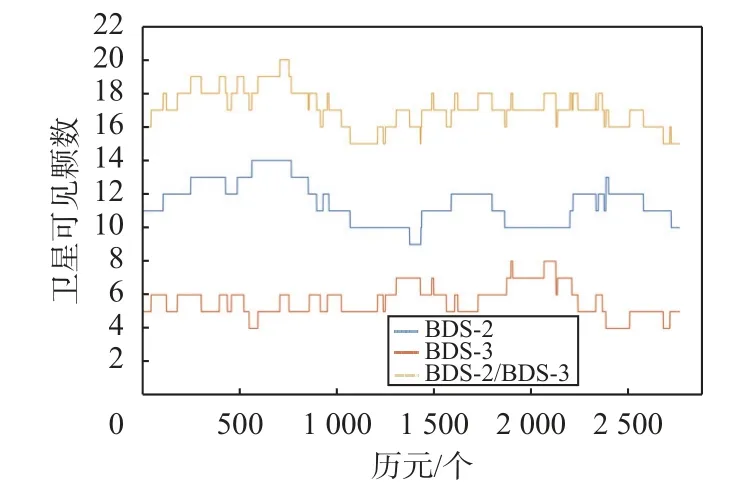
图 1 BDS-2/3卫星可见数统计图
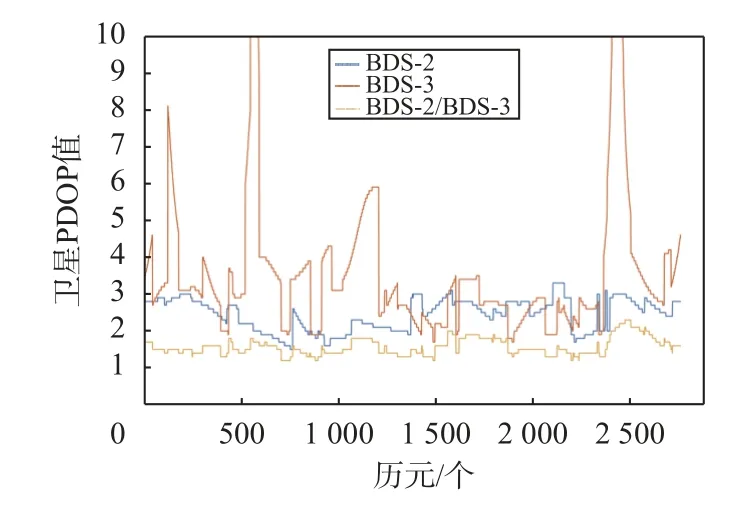
图 2 BDS-2/BDS-3卫星PDOP值统计图
实验流程具体如下:首先利用MATLAB采用并行计算的方法对不同组合的MGEX基准站与全球18个iGMAS观测站进行GDOP值计算,选择次数与对应的GDOP值如图3所示. 通过计算可知,次数达到5×107,其中最小GDOP值为0.311 9,所对应的测站组合的测站分布图如图4所示,其中红色代表18个iGMAS待测站,绿色代表采用GDOP法选择的MGEX基准站,蓝色代表利用格网法选择的MGEX基准站. 然后利用GAMIT/GLOBK 10.71版本对所选测站进行双差相对定位解算,其中BDS广播星历和精密星历选用武汉大学播发的四系统混合星历,通过对原始观测数据的质量评定,确定解算时间为2020年第96~100天共计5天的数据,对两种方法组成的控制网进行解算,具体解算参数表1所示.最后对解算的基线结果进行平差计算,获得待定点的点位坐标值,并与iGMAS各天发布的SINEX文件里的坐标值进行对比,计算出各点的点位误差值. 最终通过实验结果进行对比和分析,验证顾及GDOP值选站法的可行性.
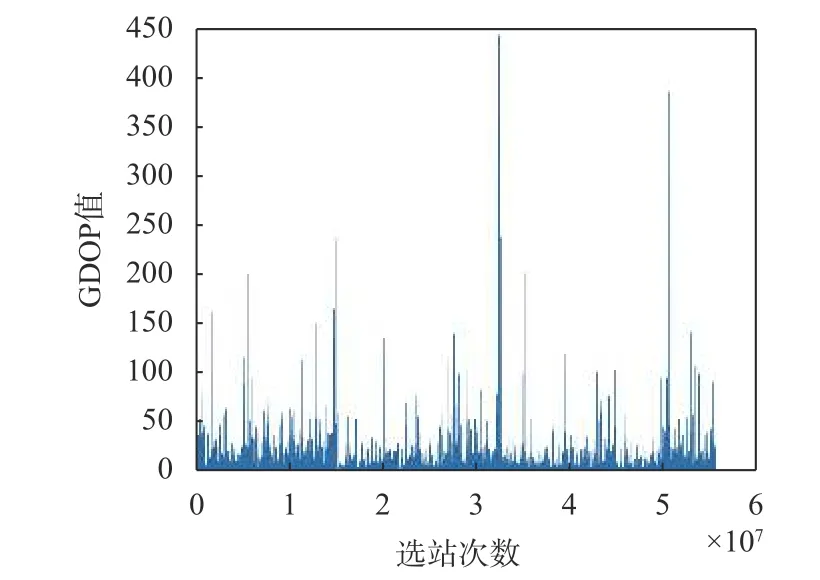
图 3 GDOP值计算统计图
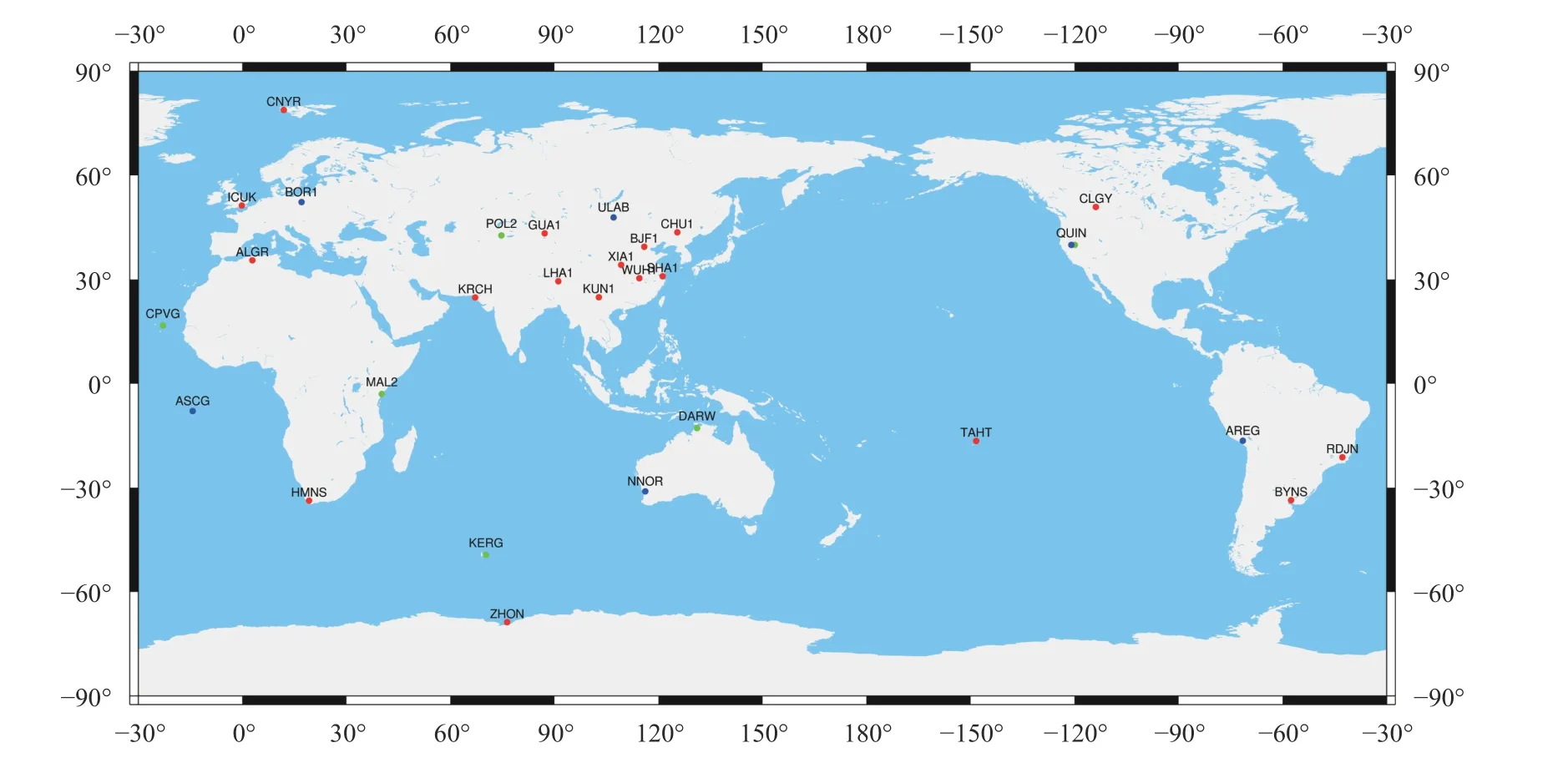
图 4 测站分布图

表 1 解算策略
2.2 基线长度标准差值
基线长度标准差值(STD)用来描述测站间的距离对基线精度的影响,同样作为评价基线解算精度的指标之一. 比较各系统解算基线长度STD值随基线长度增加的变化情况,对评价解算质量提供参考.STD值计算公式为

式中:S为基线长度标准差值;n为总观测时段;Li为第i个时段的基线解算结果;L¯ 为单天基线解得加权平均值. 本次实验解算最短基线为326.6 km,最长基线为12 737.96 km. 以基线长为横轴,对应的基线长度STD值为纵轴,统计出各方法解算基线长度STD变化如图5所示,由图5可知,整体上两方法解算的基线精度都能达到20 mm以内,精度较高,满足要求.对比可以看出,在6 000 km以内基线的精度值二者差别不大,但采用格网选站法对6 000 km以上的基线的解算精度约在20 mm,采用GDOP值选站法的解算精度较高,稳定在13 mm内,并且随着基线长度的增加对应STD值增加的趋势较为缓慢.

图 5 各方法解算基线长度STD值统计图

图 6 基线三方向精度统计图
为了更加详细的分析两种方法的解算结果,对基线东(E)、北(N)、天顶(U)三方向的中误差进行比较,以基线长度作为横轴,三方向中误差值作为纵轴,两种方法的基线三方向精度统计图如图6所示.由图6可知,整体上两方案基线在U方向上的解算精度低于E方向和N方向,属于正常现象. 采用格网法选站在6 000 km以内的基线三方向中误差只能保持在5 mm以内,6 000 km以上的一部分基线三方向中误差在5~20 mm;而采用GDOP值选站法解算的6 000 km以内的基线也优于格网法选站结果,大部分基线三方向中误差在3 mm以内,6 000 km以上的基线三方向中误差大部分位于5 mm以内,个别基线三方向中误差在5~15 mm. 可以看出,采用GDOP值选站法时对长基线的精度提升约为5 mm. 这说明采用GDOP值选站法对整个网形各个基线的精度控制能力较强,使得解算出的基线精度较高.
对两方案各天的基线解算结果进行GLOBK平差,对MGEX基准站进行强约束,解算出待定点各天的坐标值,并与iGMAS官网发布的SINEX文件中的坐标进行对比,计算出待定点在X、Y、Z三方向上的精度值如图7所示. 可以看出,整体上KRCH、SHA1、XIA1三个测站的精度较低,只能保持在10 cm以内的精度,这有可能是观测站本身数据质量较差,亦或由于起算坐标精度较低导致的. 整体上看,点位精度达到厘米级,这可能是因为控制网较大,点与点之间距离较长,但由计算可知,解算结果的相对精度较高. 单从格网法计算结果来看,大部分测站保持在2 cm以内的精度值,相比之下,采用顾及GDOP值选站法计算的大部分测站精度在1.5 cm以内,精度有所提高. 综合结果来看,采用顾及GDOP值选站法解算的基线和定位结果能够达到更高的精度.
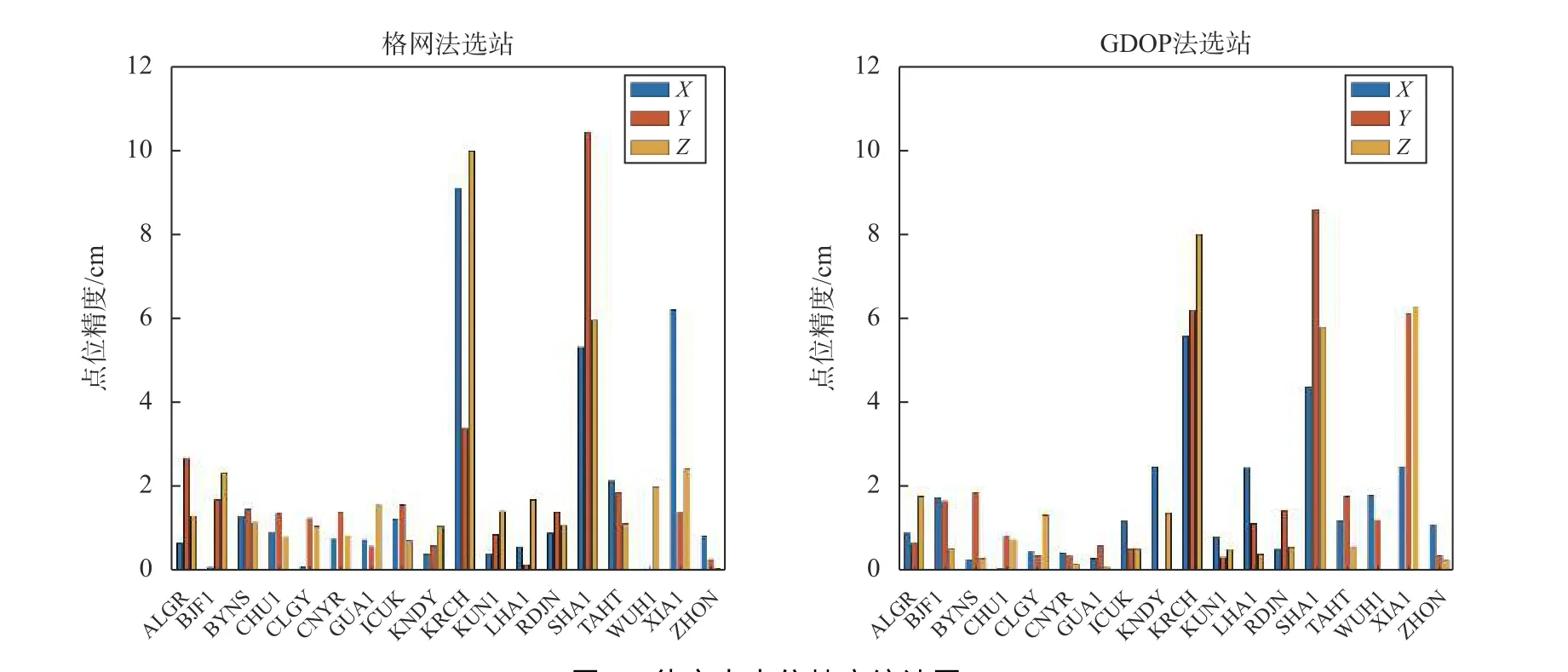
图 7 待定点点位精度统计图
3 结 论
本文提出的顾及GDOP值选站法基线解算,通过该方法分析了5天观测数据的基线相对定位解算结果,并与传统的格网法选站解算结果进行对比,得出以下结论:
1)采用顾及GDOP值选站法在基线长度STD值方面达到15 mm以内,精度优于格网法的20 mm.6 000 km内的长基线N、E、U三方向中误差也稳定在3 mm以内,优于格网法的5 mm;6 000 km以上的长基线三方向中误差大部分维持在5~15 mm,相比之下表现较好.
2)同样以原始观测文件的概略坐标为解算的初始坐标,采用顾及GDOP值选站法在待定点的解算中大部分点中误差能够达到1.5 cm以内,优于格网法2 cm中误差的解算结果.
3)相比于传统的格网选站法,采用顾及GDOP值选站法从观测方程出发,以GDOP最小值为准则,快速在众多基准站中选择出几何分布较优的测站列表,在保证计算效率的同时,提高了一定的解算精度.该方法可广泛应用于区域CORS网解算和实际生产项目的解算中.

