低轨卫星导航增强系统半物理仿真平台设计与验证
刘天立,杨轩,刘晓旭
( 卫星导航系统与装备技术国家重点实验室, 石家庄 050081 )
0 引 言
以人工智能为核心的当代产业革命态势蓬勃,机器自主与无人驾驶等领域发展迅猛,对时空信息的泛在性、快速性与精准性提出了更高地需求. 卫星导航精密单点定位(PPP)技术可以提供广域的厘米级精度定位服务,然而受限于中高轨导航卫星与地面用户之间几何构型变化缓慢,厘米级定位收敛时间长达几十分钟[1-2]. 低轨卫星相对地面几何构型变化快,与全球卫星导航系统(GNSS)组合实现的高精度精密定位技术可将收敛过程耗时压缩至分钟级,该技术为北斗卫星导航系统(BDS)PPP服务应用提供良好的低成本快速高精度解决方案. 此外低轨卫星具有播发信号链路损耗小的优点,信号落地功率能够提升30 dB以上[3],在复杂电磁环境和高纬度地域环境应用中具有独特优势. 低轨导航增强技术已成为当前卫星导航领域研究的热点[4-5].
目前国内外的低轨导航增强技术研究均处于起步阶段,美国的Iridium NEXT通信星座提供卫星时间和位置服务,定位精度只有20~50 m,此外诸如Xona Space Systems、OneWeb星座、“鸿雁”星座、“微厘空间”低轨导航星座计划等起步较晚,尚无成熟的低轨导航卫星星座[6-8],对于低轨导航增强技术的服务性能缺乏真实有效的验证手段. 卫星导航模拟技术可以模拟卫星导航信号,用于卫星导航技术的模拟验证,然而现有的卫星导航模拟平台主要面向中、高轨道卫星导航场景,并不适用于低轨星座.
综上所述,本文对低轨导航卫星轨道外推方法、低轨卫星信号捕获跟踪技术展开研究,在GNSS导航信号模拟技术基础上设计构建低轨导航增强系统半物理仿真平台,最终基于仿真平台对低轨卫星增强系统与BDS组合精密定位快速收敛性进行验证.
1 低轨卫星导航增强仿真系统架构
低轨卫星导航增强半物理仿真平台包括卫星信号模拟和导航信号处理两部分,系统方案架构如图1所示,其中卫星信号模拟部分模拟北斗与低轨增强系统卫星的射频信号;导航信号接收部分以北斗/低轨卫星增强信号联合接收机为被测设备,对模拟射频信号进行接收处理.
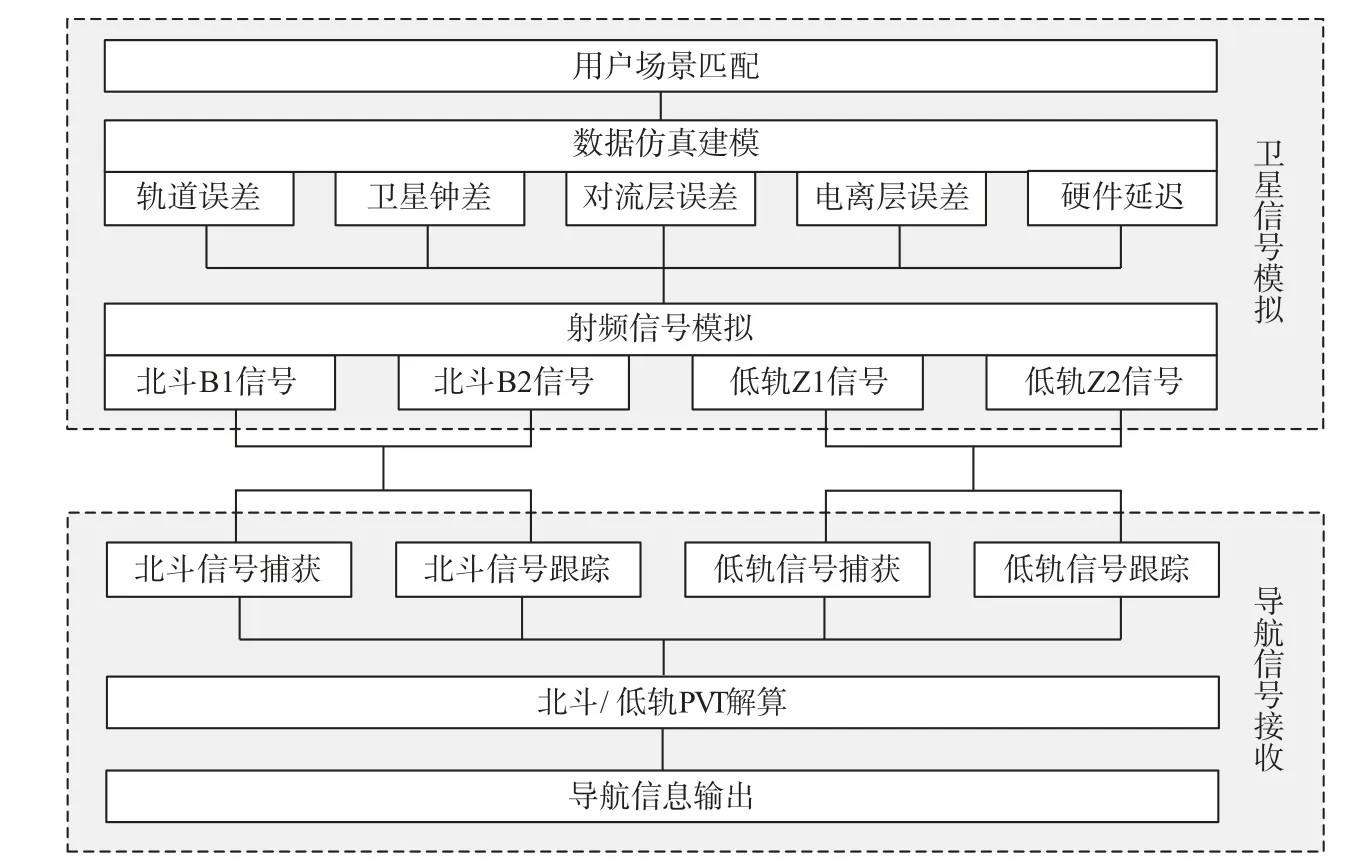
图 1 低轨卫星导航增强仿真系统设计示意图
卫星信号模拟部分完成在指定场景下,北斗/低轨卫星导航信号的数据仿真建模以及射频信号模拟.依据用户设定的场景参数,计算需求时刻卫星和用户之间的距离值及各阶距离分量,并通过叠加本时段的各种误差(如星钟、电离层、对流层等)实时生成包括观测量和导航电文信息等仿真数据,之后由模拟调制电路参照仿真数据实现伪码和电文的生成、调制及变频等,实现不同频点、不同体制的导航卫星射频信号生成. 为了极尽真实地模拟卫星信号,需要对数据仿真的空间段、环境段、用户段分别构建数学模型,包括卫星轨道动力学模型、卫星星钟模型、卫星天线方向图模型、多径模型、观测数据计算模型、用户天线方向图模型等[9-10].
导航信号接收部分完成北斗/低轨卫星射频信号的接收处理. 该部分首先对包括B1I、B1C、B2a、Z1和Z2五个频点的射频信号进行捕获、跟踪,在获取电文信息的基础上进行电文解析和卫星位置计算,利用低轨卫星、北斗卫星导航信息实现融合定位,最后输出北斗/低轨PVT解算的导航定位结果和原始观测量信息,以供评估分析. 为了使中频输出电平稳定,同时考虑到场景接收信号的强弱变化,在接收机中引入自动增益控制电路,达到稳定的输出控制.
2 低轨卫星轨道外推方法
低轨导航增强半物理仿真平台的卫星信号模拟包括BDS信号模拟和低轨导航增强卫星导航信号模拟两部分,其中BDS信号模拟技术臻于成熟,因此主要针对低轨导航增强卫星导航信号模拟展开研究.
卫星导航信号模拟的本质是对导航卫星信号观测值进行仿真,而精准的卫星动力学模型是仿真系统有效运行的基础. 由于卫星在轨运行时同时受中心力场与非中心力场的作用,二体环境下的理想情况分析不再适用. 此外,低轨卫星受到的非保守力比中高轨更为复杂,轨道摄动影响更为明显. 表1为面质比为0.01 m2/kg条件下不同轨道高度的低轨卫星受到的摄动力加速度量级,其中J2项摄动、大气阻尼、日月引力以及高阶重力场摄动是造成低轨卫星摄动误差的主要部分.
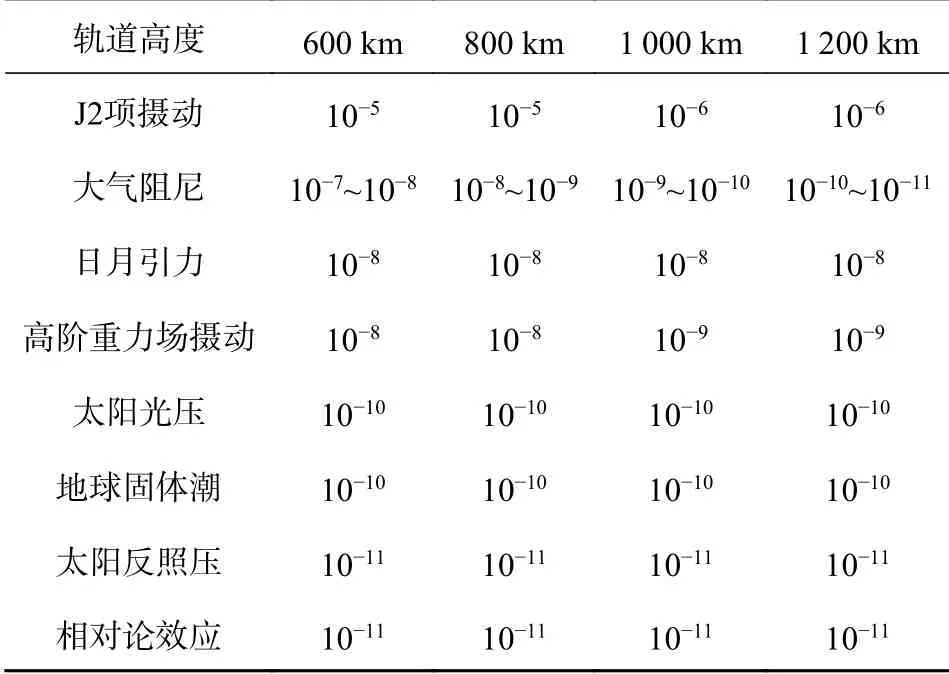
表 1 不同轨道高度低轨卫星受到的摄动力加速度量级 km/s2
J2项摄动与高阶重力场摄动均由地球非球形引力引起,地球非球形引力对在轨卫星影响产生的加速度值为地球引力势的梯度函数. 地球引力势U可以表达为地心经度φ、纬度 λ 以及地心距离r的函数,如式(1)所示,其中, µ =3.986 000 441 5×1 014 m3/s2为地球引力常数;RE为地球半径;Pn,m(X) 为关于X的m级n阶Legendre 函数;系数Cn,m、Sn,m采取EGM96模型的测量值[11].
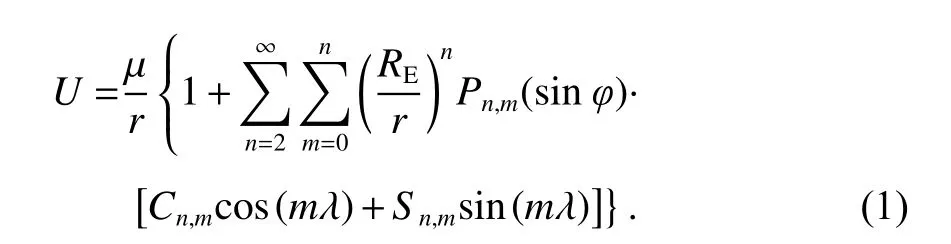
低轨卫星所处轨道比中高轨道大气密度高,所受大气阻力影响更为明显. 大气阻尼作用有阻力、升力和副法线三种作用力,其中大气升力与副法线作用力较小,可以忽略不计[12]. 对于质量为m、迎风截面为A的卫星受大气阻力影响产生的加速度有

式中:vr为卫星相对大气流的速度矢量;CD为大气阻力系数; ρ 为卫星所处的大气密度,取用Jacchia模型计算.
卫星在轨受到太阳、月球等天体的N体引力摄动,可以在地惯系中表示,摄动力加速度为
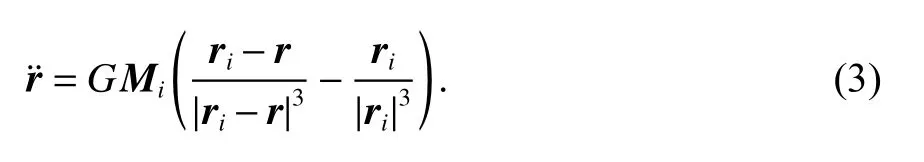
式中:G为万有引力常数;取值为6.672 59×10 N·m²/kg²;Mi和ri分别为天体的质量与在地惯系中的质点位置矢量.
对卫星受力模型进行运动方程积分可以进一步得到卫星的运动状态,高精度的积分方法是计算高精度的卫星运动轨迹的基础. 低轨卫星星座数量庞大,达到全球覆盖的需求需要上百颗卫星[13],因此应同时兼顾工程计算量的控制需求,设计合适的仿真算法.
Runge-Kutta数值积分算法是一种高精度单步算法,对卫星运动方程导数值进行线性组合,以获取高阶逼近的数值解,算法精度高,且在工程上得到了广泛应用[14],文中选取Runge-Kutta 算法进行数值积分.
对于给定计算步长为 τ 的各历元时刻卫星的轨迹信息有

式中:s为级数,对于标准的四阶Runge-Kutta算法,已知f(t,y) 为 矢量y关于变量t的一阶偏导数,关于C和ki有:
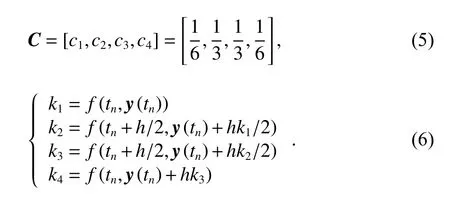
数值积分的结果与步长的取值有关,步长取值越小,数值积分精度会更高,同时计算量也会增加. 为了保障仿真数据的实时性与高保真效果,软件采用分层式仿真设计方案,将计算量较大且可以共用的卫星轨道仿真、广播星历拟合以及导航电文编码开辟多线程并行计算,并在逻辑流程层尽可能保证其提前计算,极尽可能保障软件仿真的实时性能.
3 高动态卫星信号捕获及跟踪技术
低轨卫星导航增强系统半物理仿真平台在卫星导航信号模拟的基础上通过北斗/低轨卫星增强信号联合接收机完成射频信号的接收处理. 低轨卫星运动速度比中高轨卫星快,信号的多普勒频移和加速度的变化范围均在GNSS信号的10倍以上;并且低轨卫星过境时间短,对低轨信号的跟踪弧段完整性要求更高. 因此,高动态条件下高精度的信号测量实现非常重要.
对于轨道高度800 km的低轨卫星,与地面接收机最大相对速度按8 km/s计,多普勒频偏可达40 kHz.然而,常规接收机捕获算法能捕获到的多普勒频偏范围约为±5 kHz. 由于低轨卫星的高动态特性,接收机的信号捕获过程变得更加困难.
为了解决上述问题,本文采用PMF+FFT方式使用大量并行相关器组和频率并行FFT流水模式,通过频率分块搜索的方法遍历高动态多普勒范围,在较低工作时钟情况下提高信号的捕获速度. 信号捕获流程如图2所示,采用该设计不仅能保证高动态信号的成功捕获,同时使得捕获时间处于可接受的范围.
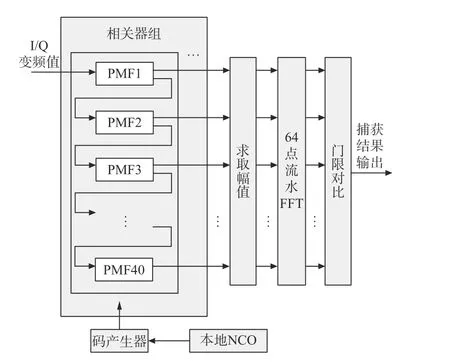
图 2 接收机捕获流程
捕获模块的输入为降采样的基带数据,输入数据与本地伪码做匹配滤波运算. 匹配滤波模块包含大量的相关器组,各个相关器组依次相差半个码片,输入信号相关运算后求取幅值以进行64点流水FFT,记录最大值结果. 然后,此最大值与门限值比较,大于门限则认为捕获成功,得到多普勒频偏和码相位的估计值. 最后,经由精捕获处理得到载波参数的估计值并传送至跟踪模块. 捕获方式采用相干积分2 ms、10次非相干累积的方式,灵敏度达到-135 dBm;频率搜索步进为20 kHz,扫频搜索4个频点,对应的捕获时间为80 ms.
接收机的动态性能主要取决于载波跟踪能力,而捕获模块得到的载波参数估计值受多普勒的影响载波和码的频率会不断发生变化,为了获取高精度的载波参数测量,需要尽量减小锁相环的测量误差. 此测量误差源主要包括相位抖动误差和动态应力误差.
相位抖动误差可以分为热噪声和基准振荡器的相位噪声. 热噪声的均方差可以通过合理调控锁相环的噪声带宽来调节,在噪声带宽很小的情况下,基准振荡器的相位噪声可以用衡量信号频率稳定度的阿仑偏差来表示. 因此,接收机对基准振荡器的信号频率稳定性有较高的要求,在实际应用中采用高稳晶振输入,确保基准振荡器的信号频率具备较高的稳定性.
对于动态应力误差,N阶锁相环的稳态跟踪误差为

式中:R代表卫星与接收机之间的连线距离;为距离对时间的N次导数. 载波跟踪选取三阶锁相环,设定环路噪声带宽为18 Hz,接收机在卫星观测方向上相对于卫星做10g/s的加速度运动时,求得Z1、Z2频点对应的3σ误差分别为14.86°和12.66°,小于二象限反正切鉴相器的180°相位牵入范围的1/4. 上述参数设计能够可以实现对低轨卫星信号的有效持续跟踪.
4 验证实验
低轨卫星的快速多普勒频率与几何变化特性可以实现PPP方法的快速收敛,本文在低轨导航增强系统仿真的基础上,对北斗/低轨导航增强组合系统环境下的PPP收敛特性进行实验验证.
实验中低轨模拟器仿真的误差模型包括电离层、对流层延迟以及卫星钟差等,播发的北斗信号有B1c和B2a信号,频率分别为1 575.42 MHz和1 176.45 MHz,低轨导航增强信号包括Z1和Z2信号,考虑到与L频段现有GNSS信号的频率兼容性,Z1和Z2频率设计为1 298.187 MHz和1 525.293 MHz. 低轨卫星星座采用极轨和中倾角混合Walker星座,轨道倾角分别为92.716°和35.208°. 其中极轨星座的轨道高度为1 361.723 km,包含9个轨道面,每个轨道面9颗卫星;中倾角星座的轨道高度为1 260.431 km,采用7个轨道面,每个轨道面9颗卫星,星座构型如图3所示.
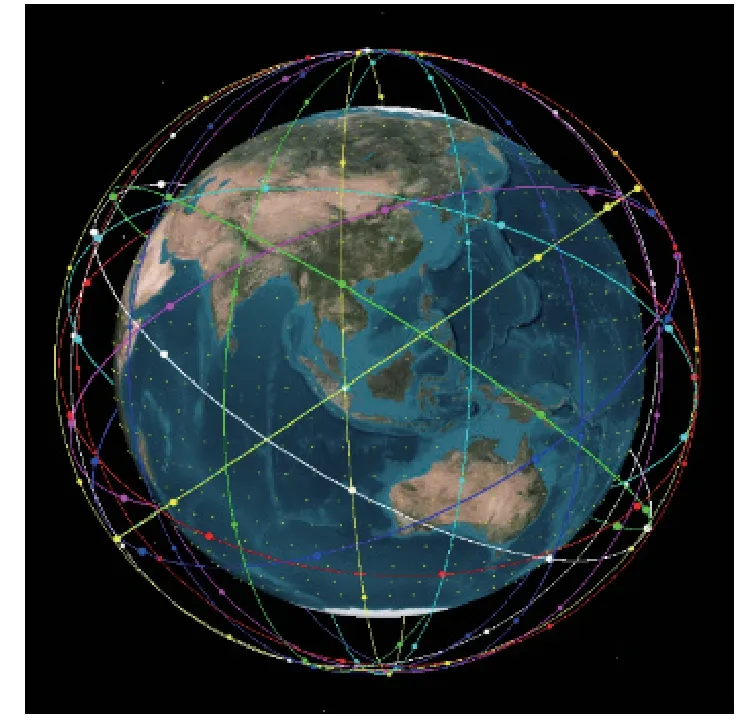
图 3 低轨导航星座构型图
低轨模拟器输出观测量的采样间隔为1 s,解算时长为2 h,截止高度角设置为5°,采用动态PPP进行解算,利用双频消电离层组合消除电离层误差低阶项,对流层延迟使用Saastamoinen模型作为先验模型计算干湿延迟,同时对湿延迟以随机游走模式进行估计. 伪距与载波噪声比设置为100:1,采用传统高度角定权策略,详细PPP解算策略设置如表2所示.

表 2 PPP解算策略
仿真实验中BDS单系统与北斗/低轨组合系统可视卫星数及位置精度因子(PDOP)值如图4所示.
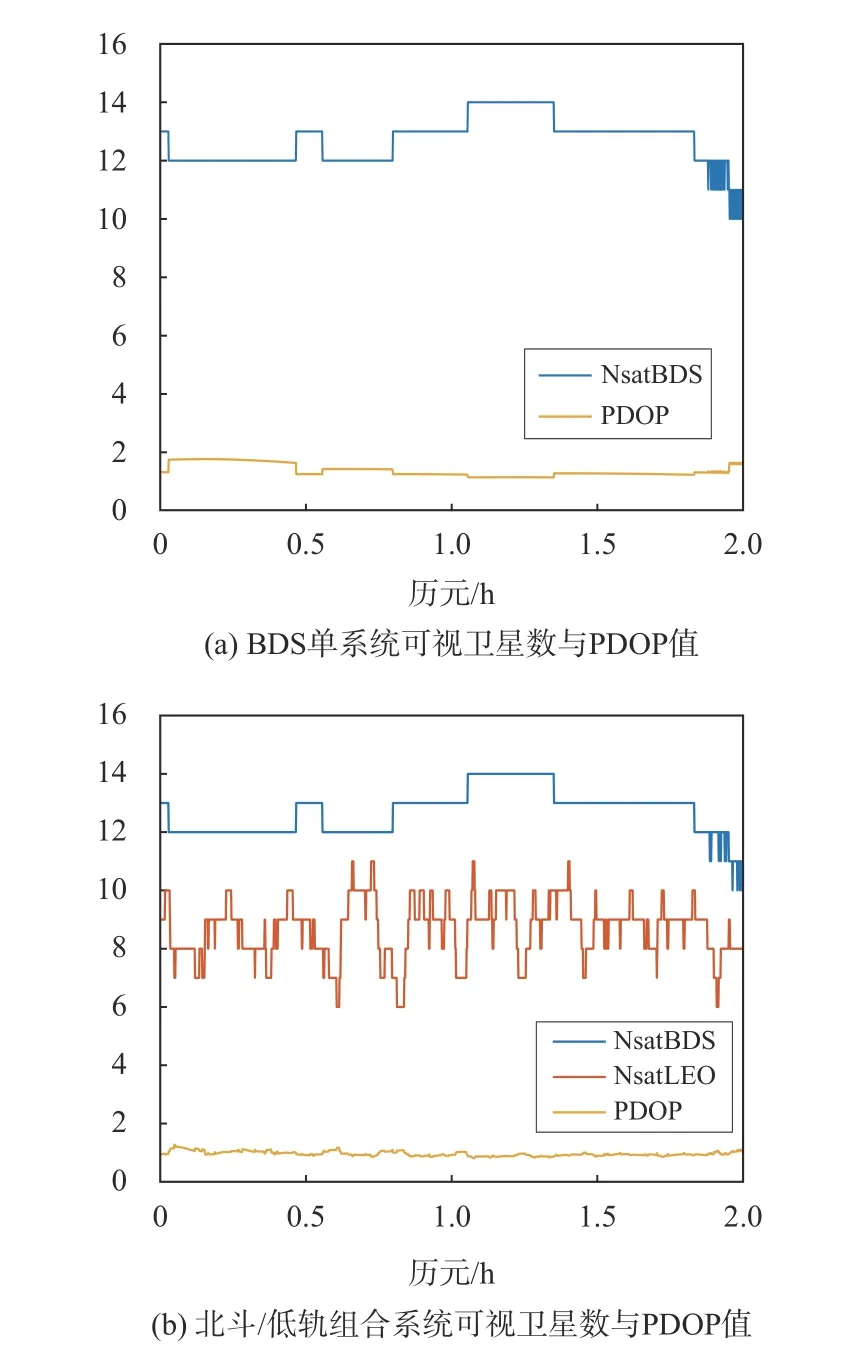
图 4 BDS单系统与北斗/低轨组合系统可视卫星数及PDOP值
利用BDS单系统数据进行PPP时,LEO可视卫星数为10~14颗,北斗与低轨双系统情况下,低轨卫星的加入使可视卫星数增加6~10颗,PDOP值可由1.39降低至0.96. 低轨卫星可视卫星数目变化剧烈,侧面显示出低轨卫星运行速度快,地面接收机捕获和失锁频繁.
低轨导航增强系统仿真PPP的实验结果如图5所示.
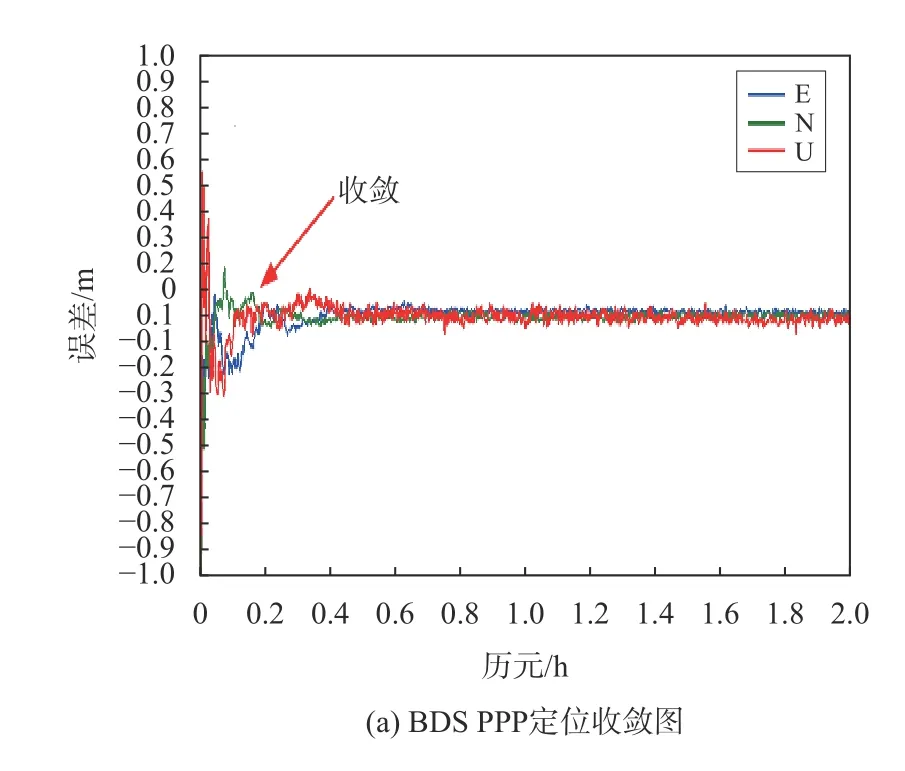
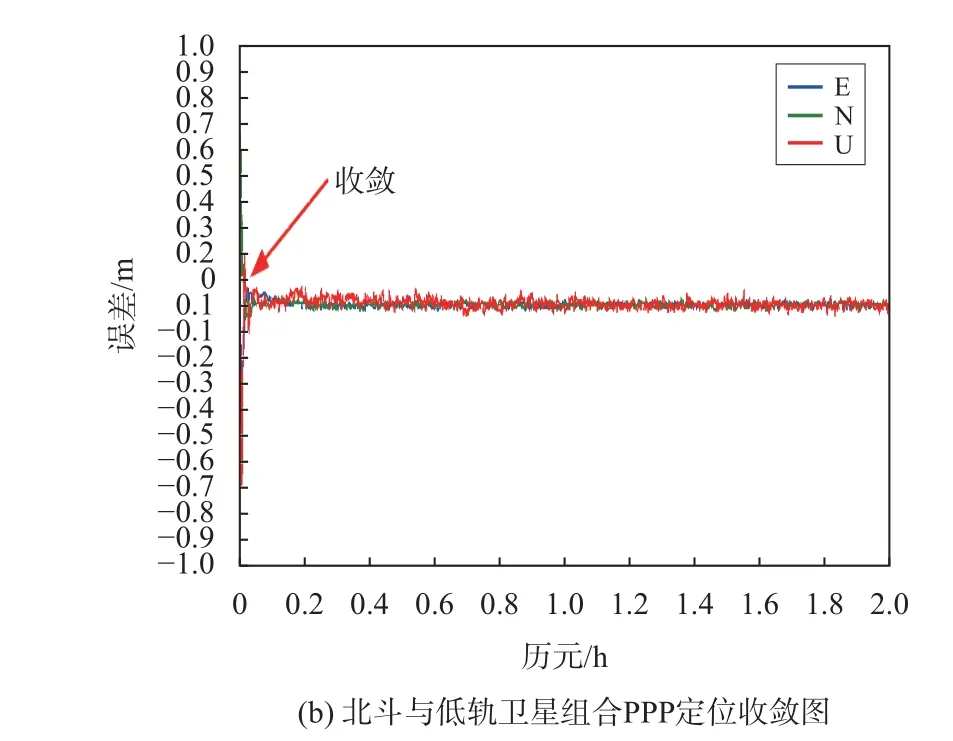
图 5 PPP收敛情况
以定位水平与高程方向误差均小于0.1 m,并在1 min内维持精度不变作为定位收敛标志,BDS单系统信号进行PPP时,定位收敛的时长约为18 min,而使用北斗与低轨组合导航信号进行PPP后,定位收敛的时间可缩短为约1 min,提升幅度达90%以上.两种情况收敛后最终定位精度均可达约2 cm,证明低轨导航增强系统仿真具有较高的内符合精度,可应用于低轨导航增强系统的技术验证.
5 结束语
针对低轨卫星导航增强系统进行半物理仿真平台设计,通过对低轨卫星轨道外推方法和高动态信号捕获及跟踪技术两方面研究,成功搭建低轨卫星导航增强系统半物理仿真平台,最后基于仿真系统进行了北斗/低轨导航增强组合系统环境下的PPP实验. 仿真验证结果表明:该系统能够实现PPP的快速收敛,并且具有较高的内符合精度. 该平台可有效应用于低轨导航增强系统仿真测试,对于未来低轨卫星导航增强系统的建设具有一定的工程价值与理论支撑作用.

